How to Find the Perimeter of a Parallelogram: A Simple and Effective Guide

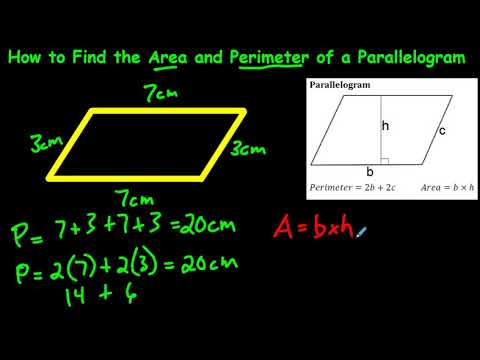
The perimeter of a parallelogram is the total length around the shape. To find the perimeter, you need to know the lengths of its sides.

Formula for the Perimeter

The formula to calculate the perimeter \( P \) of a parallelogram is:

\[ P = 2a + 2b \]

where:

• \( a \) is the length of one pair of opposite sides.
• \( b \) is the length of the other pair of opposite sides.

Steps to Calculate the Perimeter

1. Measure the lengths of one pair of opposite sides. Label this length as \( a \).
2. Measure the lengths of the other pair of opposite sides. Label this length as \( b \).
3. Substitute the values of \( a \) and \( b \) into the perimeter formula.
4. Perform the arithmetic operations to find the perimeter.

Example Calculation

Suppose a parallelogram has sides of lengths 8 cm and 5 cm. To find the perimeter:

\[ a = 8 \, \text{cm} \]

\[ b = 5 \, \text{cm} \]

Using the formula:

\[ P = 2a + 2b \]

Substitute the values of \( a \) and \( b \):

\[ P = 2(8) + 2(5) \]

\[ P = 16 + 10 \]

\[ P = 26 \, \text{cm} \]

Therefore, the perimeter of the parallelogram is 26 cm.

Additional Notes

Ensure accurate measurements of the sides to obtain the correct perimeter. The sides opposite each other in a parallelogram are always equal in length.

The perimeter of a parallelogram is a fundamental concept in geometry that is essential for understanding various properties of this unique quadrilateral. A parallelogram is a four-sided figure with opposite sides that are both equal in length and parallel. The simplicity and elegance of its structure make it a common subject in both academic studies and practical applications. In this guide, we will explore the methods to find the perimeter of a parallelogram, providing you with a comprehensive understanding that will enable you to tackle related problems with confidence.

To start, it's important to recognize that the perimeter of any polygon is the total length of its boundaries. For a parallelogram, this involves calculating the sum of the lengths of all its sides. Given the properties of a parallelogram, where opposite sides are equal, the formula for the perimeter can be simplified. This guide will take you through each step of the process, from understanding the basic properties of parallelograms to applying the perimeter formula in various scenarios.

Whether you are a student looking to excel in your geometry class or a professional needing a refresher, this guide will serve as a valuable resource. We will cover:

• The definition and properties of parallelograms
• The formula used to calculate the perimeter
• Detailed, step-by-step instructions for finding the perimeter
• Practical examples to illustrate the concepts
• Special cases and considerations you may encounter
• Real-world applications of perimeter calculations
• Common mistakes and how to avoid them
• Answers to frequently asked questions

By the end of this guide, you will have a thorough understanding of how to find the perimeter of a parallelogram, equipped with the knowledge and skills to apply these concepts effectively. Let's begin our journey into the world of parallelograms and uncover the simplicity and beauty of their perimeter calculations.

A parallelogram is a four-sided polygon (quadrilateral) with opposite sides that are both parallel and equal in length. It has several distinctive properties that set it apart from other quadrilaterals.

• Opposite Sides are Parallel and Equal: In a parallelogram, each pair of opposite sides are parallel and equal in length.
• Opposite Angles are Equal: The angles opposite each other in a parallelogram are equal. If angle A is opposite angle B, then ∠A = ∠B.
• Adjacent Angles are Supplementary: Adjacent angles in a parallelogram add up to 180 degrees (supplementary). This means ∠A + ∠B = 180°.
• Diagonals Bisect Each Other: The diagonals of a parallelogram intersect each other at their midpoints, effectively bisecting one another.

Properties of Parallelograms

Understanding these properties helps in identifying parallelograms and differentiating them from other quadrilaterals like rectangles, rhombuses, and squares, which are specific types of parallelograms with additional properties.

• A rectangle is a parallelogram with four right angles.
• A rhombus is a parallelogram with all sides of equal length.
• A square is a parallelogram with four equal sides and four right angles.

Mathematical Representation

Let’s represent a parallelogram mathematically:

• Sides: Denoted by \( a \) and \( b \), where \( a \) is the length of one pair of opposite sides, and \( b \) is the length of the other pair.
• Angles: Denoted by \( \alpha \) and \( \beta \), where \( \alpha \) is the measure of one pair of opposite angles, and \( \beta \) is the measure of the other pair.
• Diagonals: Denoted by \( d_1 \) and \( d_2 \), which intersect and bisect each other at right angles.

These properties are crucial when calculating the perimeter and area of parallelograms and understanding their behavior in various geometric contexts.

In conclusion, the defining characteristics of parallelograms make them unique and identifiable among quadrilaterals, serving as foundational elements in geometry and numerous practical applications.

The perimeter of a geometrical shape is the total distance around its outer edge. For a polygon, the perimeter is the sum of the lengths of all its sides. In the case of a parallelogram, which is a specific type of polygon, the perimeter can be calculated by adding together the lengths of its four sides.

A parallelogram is defined by having opposite sides that are both equal in length and parallel. This property allows us to simplify the formula for calculating its perimeter.

For a parallelogram with side lengths \(a\) and \(b\), the perimeter \(P\) is given by the formula:

\[ P = 2a + 2b \]

This can be further simplified to:

\[ P = 2(a + b) \]

Here's how to find the perimeter step-by-step:

1. Identify the lengths of the two distinct sides of the parallelogram, \(a\) and \(b\).
2. Use the formula \(P = 2(a + b)\) to calculate the perimeter.
3. Multiply the sum of \(a\) and \(b\) by 2 to get the total perimeter.

For example, if a parallelogram has sides of lengths 7 cm and 5 cm, the perimeter would be calculated as follows:

• First, add the lengths of the two sides: \(7 + 5 = 12\) cm.
• Then, multiply this sum by 2: \(2 \times 12 = 24\) cm.

Therefore, the perimeter of the parallelogram is 24 cm.

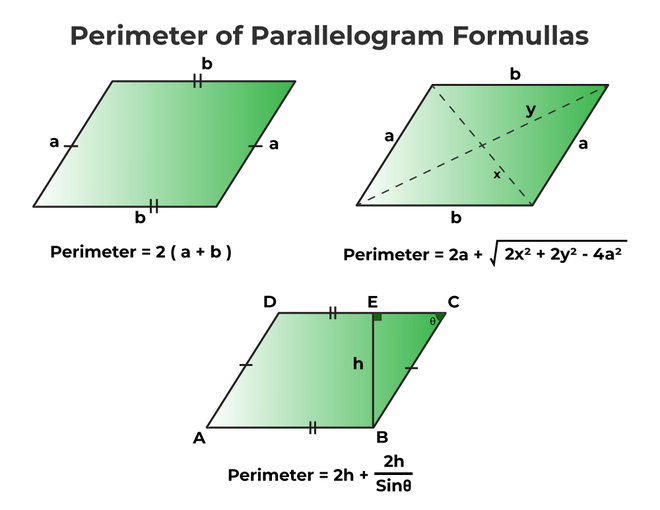
The perimeter of a parallelogram is the total distance around the outside of the shape. To find the perimeter, you need to know the lengths of the parallelogram's sides. There are several formulas you can use depending on the information available:

Basic Perimeter Formula

If you know the lengths of the two adjacent sides of the parallelogram, \( a \) and \( b \), the formula for the perimeter \( P \) is:

\[ P = 2(a + b) \]

For example, if a parallelogram has sides of lengths 5 units and 9 units:

• Given: \( a = 5 \) units, \( b = 9 \) units
• Perimeter: \( P = 2(5 + 9) = 2 \times 14 = 28 \) units

Using Side and Diagonals

If you know one side and the lengths of both diagonals, \( x \) and \( y \), the formula is:

\[ P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2} \]

For example, if a side length is 7 units and the diagonals are 8 units and 10 units:

• Given: \( a = 7 \) units, \( x = 8 \) units, \( y = 10 \) units
• Perimeter: \( P = 2(7) + \sqrt{2(8)^2 + 2(10)^2 - 4(7)^2} \)
• Simplified: \( P = 14 + \sqrt{128 + 200 - 196} = 14 + \sqrt{132} \approx 14 + 11.49 = 25.49 \) units

Using Side, Height, and Angle

If you know one side, the height, and an angle, the formula is:

\[ P = 2a + \frac{2h}{\sin \theta} \]

For example, if a side length is 15 yards, height is 20 yards, and the angle is 30 degrees:

• Given: \( a = 15 \) yards, \( h = 20 \) yards, \( \theta = 30^\circ \)
• Perimeter: \( P = 2(15) + \frac{2(20)}{\sin 30^\circ} = 30 + \frac{40}{0.5} = 30 + 80 = 110 \) yards

Important Notes

• The perimeter of a parallelogram is the sum of all its sides.
• Ensure the measurements are in the same units before calculating.

Calculating the perimeter of a parallelogram is a straightforward process that involves a few simple steps. Here's how to do it:

1. Identify the lengths of the adjacent sides:

   Let's call the lengths of the adjacent sides \(a\) and \(b\). These are the sides that share a common vertex.

2. Add the lengths of the adjacent sides:

   Calculate the sum of the lengths of these two sides: \(a + b\).

3. Multiply the sum by 2:

   Since the opposite sides of a parallelogram are equal, you need to account for both pairs of opposite sides. Therefore, multiply the sum by 2 to get the total perimeter: \(P = 2(a + b)\).

Here's an example to illustrate the process:

• Example:

  Suppose you have a parallelogram with side lengths \(a = 8\) cm and \(b = 5\) cm. To find the perimeter:

  1. Identify the side lengths: \(a = 8\) cm and \(b = 5\) cm.
  2. Add the side lengths: \(a + b = 8 + 5 = 13\) cm.
  3. Multiply the sum by 2: \(P = 2 \times 13 = 26\) cm.

  Therefore, the perimeter of the parallelogram is 26 cm.

Using these steps, you can easily calculate the perimeter of any parallelogram as long as you know the lengths of its adjacent sides. This method is practical and efficient for various mathematical and real-world applications.

To solidify our understanding of finding the perimeter of a parallelogram, let's work through a few examples step-by-step.

Example 1

Find the perimeter of a parallelogram with adjacent sides measuring 5 units and 9 units.

• Step 1: Identify the lengths of the adjacent sides. Let \(a = 5\) units and \(b = 9\) units.
• Step 2: Use the perimeter formula \(P = 2(a + b)\).
• Step 3: Substitute the values into the formula:
  \(P = 2(5 + 9) = 2 \times 14 = 28\) units.

Therefore, the perimeter of the parallelogram is 28 units.

Example 2

Calculate the perimeter of a parallelogram with one side measuring 7 units and diagonals measuring 8 units and 10 units.

• Step 1: Identify the known values: \(a = 7\) units, \(x = 8\) units, \(y = 10\) units.
• Step 2: Use the formula for perimeter when a side and diagonals are given:
  \(P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2}\).
• Step 3: Substitute the values into the formula:
  \(P = 2(7) + \sqrt{2(8)^2 + 2(10)^2 - 4(7)^2}\)
  \(P = 14 + \sqrt{2 \times 64 + 2 \times 100 - 4 \times 49}\)
  \(P = 14 + \sqrt{128 + 200 - 196}\)
  \(P = 14 + \sqrt{132}\)
  \(P = 14 + 11.49 = 25.49\) units.

Hence, the perimeter of the parallelogram is approximately 25.49 units.

Example 3

Determine the length of another side of the parallelogram if one side is 15 yards, its corresponding height is 20 yards, and one of the vertex angles is 30 degrees.

• Step 1: Identify the given values: \(a = 15\) yards, \(h = 20\) yards, \(\theta = 30^\circ\).
• Step 2: Use the formula for perimeter involving height and angle:
  \(P = 2a + \frac{2h}{\sin \theta}\).
• Step 3: Substitute the values into the formula:
  \(P = 2(15) + \frac{2 \times 20}{\sin 30^\circ}\)
  \(P = 30 + \frac{40}{0.5}\)
  \(P = 30 + 80 = 110\) yards.

Thus, the perimeter of the parallelogram is 110 yards.

Example 4

Find the length of the other side of a parallelogram if its perimeter is 48 cm and one side is 16 cm.

• Step 1: Given values: \(P = 48\) cm, \(a = 16\) cm.
• Step 2: Use the formula \(P = 2(a + b)\) to find \(b\).
• Step 3: Substitute the known values:
  \(48 = 2(16 + b)\)
  \(48 = 32 + 2b\)
  \(16 = 2b\)
  \(b = 8\) cm.

Therefore, the length of the other side is 8 cm.

When calculating the perimeter of a parallelogram, there are several special cases and considerations to keep in mind. These cases often involve specific types of parallelograms, such as rectangles, rhombuses, and squares, which have unique properties affecting their perimeter calculations.

Rectangles

A rectangle is a parallelogram where all angles are right angles (90°). The opposite sides are equal and parallel. The formula for the perimeter of a rectangle is:

\[ P = 2(l + w) \]

where \( l \) is the length and \( w \) is the width. Since the opposite sides are equal, this formula simplifies the calculation by only requiring the lengths of two adjacent sides.

Rhombuses

A rhombus is a special type of parallelogram where all four sides are of equal length. Additionally, the diagonals of a rhombus bisect each other at right angles. The perimeter of a rhombus is:

\[ P = 4s \]

where \( s \) is the length of one side. This makes the calculation straightforward as you only need to know the length of one side.

Squares

A square is both a rectangle and a rhombus, meaning all sides are equal and all angles are right angles. The formula for the perimeter of a square is:

\[ P = 4a \]

where \( a \) is the length of a side. Like the rhombus, the perimeter calculation for a square is simplified due to the equality of all sides.

Considerations

• When given the lengths of the diagonals instead of the sides, use the properties of the special parallelograms to find the side lengths if possible. For instance, in a rhombus, the diagonals are perpendicular bisectors, and you can use the Pythagorean theorem to find the side lengths.
• Ensure you accurately identify the type of parallelogram you are working with, as this will dictate the appropriate perimeter formula and any simplifications that can be made.
• In real-world applications, always double-check measurements and ensure the given values correspond to the properties of the shape in question.

Understanding the perimeter of a parallelogram is essential not only in theoretical geometry but also in various practical applications across different fields. Here are some ways in which the concept is applied:

• Architecture and Construction

  Architects and builders often encounter parallelogram-shaped structures or components. Calculating the perimeter helps determine the amount of materials needed for construction, such as framing, molding, or edging. For example, knowing the perimeter is crucial when measuring materials for a room’s baseboard or crown molding.

• Engineering

  In engineering, particularly in structural and mechanical engineering, parallelograms are used in the design of trusses, supports, and frameworks. Understanding the perimeter is important for assessing the stability and load distribution of these components. Accurate calculations ensure that the structures can withstand the required forces and stresses.

• Graphic Design and Art

  Graphic designers and artists use parallelograms in their work to create visually appealing compositions. The properties of parallelograms, such as symmetry and balance, help in arranging elements in a harmonious manner. Knowing the perimeter aids in precise measurements and placements of design elements.

• Carpentry and DIY Projects

  Carpenters and DIY enthusiasts frequently work with parallelogram shapes when crafting furniture, frames, or decorative items. Calculating the perimeter ensures accurate cutting and fitting of pieces, leading to better-finished products.

• Mathematics Education

  Teaching the concept of perimeter using parallelograms helps students understand basic geometric principles. It also provides a foundation for more advanced topics in mathematics, such as vector geometry and trigonometry, where parallelograms play a significant role.

These practical applications highlight the importance of mastering the calculation of the perimeter of parallelograms, demonstrating its relevance in both everyday tasks and specialized professional fields.

When calculating the perimeter of a parallelogram, there are several common mistakes that students and learners often make. Here are some important points to keep in mind to avoid these errors:

• Confusing the Formula: The perimeter of a parallelogram is calculated as P = 2(a + b), where a and b are the lengths of the adjacent sides. Ensure that you are using the correct sides in your calculations.
• Incorrectly Identifying Sides: Make sure to correctly identify and use the adjacent sides of the parallelogram. Sometimes, diagonals or non-adjacent sides are mistakenly used in place of adjacent sides.
• Misinterpreting the Shape: Parallelograms have opposite sides that are equal in length. Ensure you are not confusing parallelograms with other quadrilaterals like rectangles, squares, or rhombuses, which have different properties.
• Neglecting Units: Always include and be consistent with units of measurement (e.g., cm, m, inches). Omitting units can lead to confusion and incorrect answers.
• Rounding Errors: When dealing with decimals, be cautious with rounding. Rounding too early in the calculation can result in significant errors in the final perimeter value.
• Forgetting All Sides: Remember that the perimeter is the total distance around the shape, so both pairs of opposite sides must be included in the calculation.
• Incorrect Use of Diagonal-Based Formulas: If using a formula that involves diagonals, such as P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2}, make sure to apply it correctly and understand each term.

By being aware of these common mistakes, you can ensure accurate and reliable calculations of the perimeter of a parallelogram.

• What is the formula for the perimeter of a parallelogram?

  The formula to calculate the perimeter of a parallelogram is \( P = 2(a + b) \), where \( a \) and \( b \) are the lengths of the adjacent sides.

• How do you find the perimeter of a parallelogram if only one side length is known?

  If only one side length is known, you need additional information such as the length of the diagonals or an angle. For example, if the length of one side \( a \) and the lengths of the diagonals \( x \) and \( y \) are known, you can use the formula \( P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2} \).

• Can a parallelogram have sides of different lengths?

  Yes, a parallelogram can have sides of different lengths. However, the opposite sides of a parallelogram are always equal in length.

• Is there a direct relationship between the area and the perimeter of a parallelogram?

  No, there is no direct mathematical relationship between the area and the perimeter of a parallelogram. The area depends on the base and height, while the perimeter depends on the lengths of the sides.

• What are some common mistakes to avoid when calculating the perimeter of a parallelogram?

  Common mistakes include confusing the perimeter with the area, using incorrect side lengths, and forgetting that the opposite sides of a parallelogram are equal.

• How is the perimeter of a parallelogram different from the perimeter of a rectangle?

  The perimeter of a rectangle is calculated in the same way as that of a parallelogram since a rectangle is a special type of parallelogram with right angles. The formula is \( P = 2(l + w) \) for a rectangle, where \( l \) is the length and \( w \) is the width.

• Can two parallelograms have the same perimeter but different areas?

  Yes, two parallelograms can have the same perimeter but different areas. The area depends on the base, height, and angle between the sides, while the perimeter depends only on the side lengths.

• How can the perimeter of a parallelogram be useful in real-life applications?

  The perimeter of a parallelogram can be useful in various real-life applications such as determining the length of materials needed for framing or fencing, calculating the border length for landscaping, and more.

Calculating the perimeter of a parallelogram is a straightforward process that requires understanding its geometric properties and applying a simple formula. The perimeter is determined by the sum of all sides, which, due to the nature of parallelograms, can be simplified to twice the sum of its two adjacent sides. The formula is:

\[ \text{Perimeter} = 2 \times (\text{Side}_1 + \text{Side}_2) \]

This guide has outlined the essential steps to calculate the perimeter, highlighted key properties of parallelograms, and provided practical examples to illustrate the method. Here are the key points to remember:

• A parallelogram is a four-sided polygon with opposite sides that are both equal and parallel.
• The perimeter formula, \( 2 \times (\text{Side}_1 + \text{Side}_2) \), simplifies the process by leveraging the equality of opposite sides.
• Real-world applications of this calculation include architectural design, construction planning, and engineering projects, where accurate perimeter measurements are crucial for material estimation and structural integrity.

By mastering this calculation, you can effectively determine the perimeter of any parallelogram, ensuring precision in both academic and professional settings.

We hope this comprehensive guide has clarified the process and utility of finding the perimeter of a parallelogram. Whether for educational purposes or practical applications, understanding this concept is valuable and widely applicable.