Topic find the perimeter of a parallelogram: In this article, you'll learn how to find the perimeter of a parallelogram with simple, easy-to-follow steps. Understanding the perimeter calculation is crucial for various mathematical applications and problems. Let's dive into the basics, explore key properties, and provide practical examples to make mastering this concept straightforward and accessible for everyone.
Table of Content
- Find the Perimeter of a Parallelogram
- Introduction
- Definition of a Parallelogram
- Basic Properties of a Parallelogram
- Formula for Finding the Perimeter
- Step-by-Step Guide to Calculate the Perimeter
- Example Calculations
- Common Mistakes to Avoid
- Applications of Perimeter Calculation
- Advanced Problems and Solutions
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Video hướng dẫn chi tiết cách tìm diện tích và chu vi hình bình hành, phù hợp với từ khóa 'find the perimeter of a parallelogram'.
Find the Perimeter of a Parallelogram
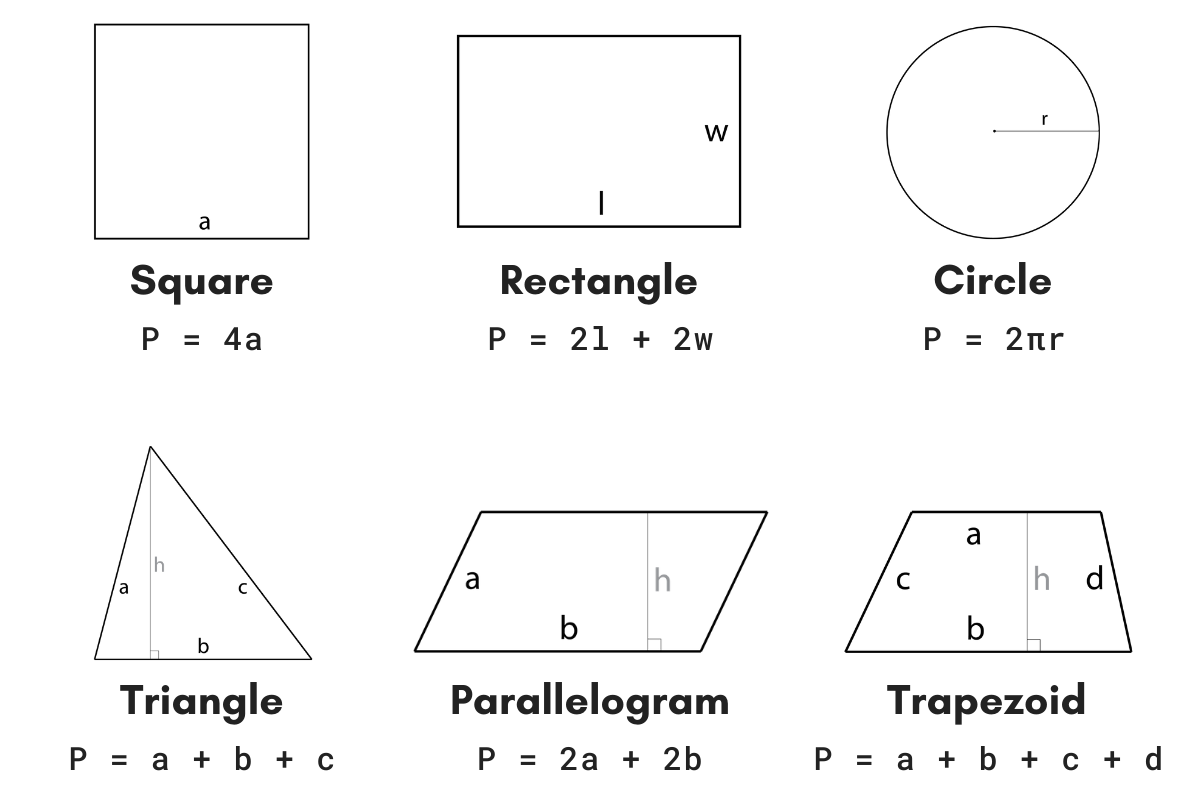
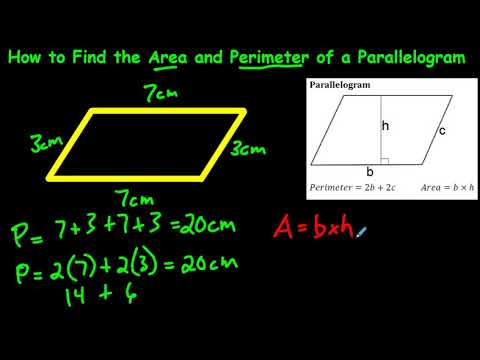
A parallelogram is a four-sided figure with opposite sides that are equal in length and parallel. The perimeter of a parallelogram is the total distance around the shape. To find the perimeter, you need to know the lengths of two adjacent sides.
Formula
The formula to calculate the perimeter of a parallelogram is given by:
\[
P = 2(a + b)
\]
where \( a \) and \( b \) are the lengths of the two adjacent sides.
Steps to Calculate the Perimeter
- Identify the lengths of the two adjacent sides, \( a \) and \( b \).
- Substitute these values into the formula \( P = 2(a + b) \).
- Simplify the expression to find the perimeter.
Example Calculation
Suppose you have a parallelogram with side lengths \( a = 5 \) cm and \( b = 7 \) cm. To find the perimeter:
\[
P = 2(a + b) = 2(5 \, \text{cm} + 7 \, \text{cm}) = 2 \times 12 \, \text{cm} = 24 \, \text{cm}
\]
Therefore, the perimeter of the parallelogram is 24 cm.
Properties of a Parallelogram
- Opposite sides are equal and parallel.
- Opposite angles are equal.
- The diagonals bisect each other.
- The adjacent angles are supplementary (sum up to \(180^\circ\)).
Applications
Understanding how to find the perimeter of a parallelogram is useful in various real-world applications, such as:
- Calculating the boundary length for fencing a parallelogram-shaped plot of land.
- Determining the amount of trim needed for a parallelogram-shaped window or picture frame.

READ MORE:
Introduction
Understanding how to find the perimeter of a parallelogram is essential for students and professionals dealing with geometry. A parallelogram is a four-sided figure with opposite sides that are both equal and parallel. Calculating its perimeter involves summing the lengths of all its sides. This guide will walk you through the definition, properties, and formula needed for this calculation, ensuring you grasp the concept fully.
- Definition: A parallelogram is a quadrilateral with opposite sides that are equal and parallel.
- Basic Properties: The opposite angles are equal, and the diagonals bisect each other.
- Perimeter Formula: The perimeter (\(P\)) of a parallelogram is given by \(P = 2(a + b)\), where \(a\) and \(b\) are the lengths of the adjacent sides.
With this foundational understanding, let's explore the step-by-step process to calculate the perimeter, examine example calculations, and discuss common mistakes to avoid.
Definition of a Parallelogram
A parallelogram is a specific type of quadrilateral that has some unique properties. Understanding these properties is key to recognizing and working with parallelograms in geometric problems.
- Opposite Sides are Parallel and Equal: In a parallelogram, both pairs of opposite sides are parallel to each other. This can be expressed as \(AB \parallel CD\) and \(BC \parallel AD\). Additionally, these opposite sides are equal in length, so \(AB = CD\) and \(BC = AD\).
- Opposite Angles are Equal: The opposite angles in a parallelogram are equal. Therefore, if one angle is \( \theta \), the angle directly opposite to it is also \( \theta \).
- Adjacent Angles are Supplementary: Adjacent angles in a parallelogram add up to 180 degrees. For example, \( \angle A + \angle B = 180^\circ \).
- Diagonals Bisect Each Other: The diagonals of a parallelogram intersect at their midpoints. This means that each diagonal splits the parallelogram into two congruent triangles, and the point of intersection divides each diagonal into two equal halves.
These properties are visually represented in the diagram below:
| Shape: |

|
| Properties: |
|
With these characteristics in mind, identifying a parallelogram and understanding its properties becomes more intuitive, forming a strong foundation for calculating its perimeter.
Basic Properties of a Parallelogram
Parallelograms are versatile geometric shapes with several key properties that are crucial for solving related problems. Here, we outline the fundamental properties of parallelograms, providing a comprehensive understanding of their geometric characteristics.
- Opposite Sides are Equal and Parallel: In any parallelogram, the lengths of opposite sides are equal. If a parallelogram has sides \(AB\), \(BC\), \(CD\), and \(DA\), then \(AB = CD\) and \(BC = DA\). Additionally, these opposite sides are parallel, denoted as \(AB \parallel CD\) and \(BC \parallel DA\).
- Opposite Angles are Equal: The opposite angles in a parallelogram are congruent. For instance, if \(\angle A\) and \(\angle C\) are opposite angles, then \(\angle A = \angle C\). Similarly, \(\angle B = \angle D\).
- Adjacent Angles are Supplementary: Each pair of adjacent angles in a parallelogram adds up to \(180^\circ\). Therefore, \(\angle A + \angle B = 180^\circ\), \(\angle B + \angle C = 180^\circ\), and so on.
- Diagonals Bisect Each Other: The diagonals of a parallelogram intersect at their midpoints, dividing each other into two equal parts. If the diagonals are \(AC\) and \(BD\), then \(AO = OC\) and \(BO = OD\), where \(O\) is the intersection point.
These properties can be summarized in the following table:
| Property | Description |
|---|---|
| Opposite Sides | Equal and parallel, \(AB = CD\) and \(BC = DA\); \(AB \parallel CD\) and \(BC \parallel DA\) |
| Opposite Angles | Equal, \(\angle A = \angle C\) and \(\angle B = \angle D\) |
| Adjacent Angles | Supplementary, \(\angle A + \angle B = 180^\circ\) |
| Diagonals | Bisect each other, \(AO = OC\) and \(BO = OD\) |
Understanding these basic properties is essential for solving problems involving parallelograms, including calculating their perimeter, area, and angles. This knowledge provides a solid foundation for more advanced geometric concepts and applications.
Formula for Finding the Perimeter
The perimeter of a parallelogram can be found using the formula:
\[ P = 2(a + b) \]
Where:
- a is the length of one pair of opposite sides (base).
- b is the length of the other pair of opposite sides (side).
Here are the steps to find the perimeter of a parallelogram:
- Measure the length of one side of the parallelogram (a).
- Measure the length of the adjacent side of the parallelogram (b).
- Add the lengths of these two sides: \( a + b \).
- Multiply the sum by 2 to get the perimeter: \( P = 2(a + b) \).
Let's look at a quick example:
If the lengths of the sides of a parallelogram are 5 cm and 8 cm:
- Let \( a = 5 \) cm
- Let \( b = 8 \) cm
Calculate the sum of the sides: \( 5 + 8 = 13 \).
Then, multiply by 2 to find the perimeter: \( P = 2 \times 13 = 26 \) cm.
Thus, the perimeter of the parallelogram is 26 cm.

Step-by-Step Guide to Calculate the Perimeter
The perimeter of a parallelogram is the total distance around its edges. To calculate it, you need to know the lengths of its sides. Here is a step-by-step guide:
-
Identify the side lengths: A parallelogram has two pairs of opposite sides that are equal in length. Let's denote the lengths of these sides as \( a \) and \( b \).
-
Use the perimeter formula: The formula to find the perimeter \( P \) of a parallelogram is:
\[ P = 2(a + b) \]
-
Plug in the side lengths: Substitute the values of \( a \) and \( b \) into the formula. For example, if \( a = 5 \, \text{units} \) and \( b = 7 \, \text{units} \), the calculation would be:
\[ P = 2(5 + 7) = 2 \times 12 = 24 \, \text{units} \]
Alternative Method: Using One Side and Diagonals
In some cases, you might know one side length and the lengths of the diagonals. The formula for the perimeter in this scenario is:
\[ P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2} \]
-
Identify the known values: Let \( a \) be the known side length, and \( x \) and \( y \) be the lengths of the diagonals.
-
Plug in the values: Substitute the values of \( a \), \( x \), and \( y \) into the formula. For instance, if \( a = 7 \, \text{units} \), \( x = 10 \, \text{units} \), and \( y = 12 \, \text{units} \), the calculation would be:
\[ P = 2(7) + \sqrt{2(10)^2 + 2(12)^2 - 4(7)^2} \]
\[ P = 14 + \sqrt{200 + 288 - 196} \]
\[ P = 14 + \sqrt{292} \approx 14 + 17.09 = 31.09 \, \text{units} \]
Tips:
- Ensure that all measurements are in the same unit before performing calculations.
- If only one side and the height are known, you can use trigonometric relationships to find the missing side lengths and then apply the perimeter formula.
Example Calculations
Below are example calculations for finding the perimeter of a parallelogram using different sets of given information.
Example 1: Using Adjacent Sides
Find the perimeter of a parallelogram whose adjacent sides are 7 cm and 10 cm.
- Identify the side lengths: \(a = 7 \, \text{cm}\) and \(b = 10 \, \text{cm}\).
- Use the perimeter formula for a parallelogram: \(P = 2(a + b)\).
- Substitute the values into the formula:
\[
P = 2(7 + 10) = 2 \times 17 = 34 \, \text{cm}
\] - Thus, the perimeter is 34 cm.
Example 2: Using One Side and Diagonals
Find the perimeter of a parallelogram with one side length of 8 cm and diagonals of 10 cm and 12 cm.
- Identify the given values: \(a = 8 \, \text{cm}\), \(x = 10 \, \text{cm}\), \(y = 12 \, \text{cm}\).
- Use the perimeter formula involving one side and diagonals:
\[
P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2}
\] - Substitute the values into the formula:
\[
P = 2(8) + \sqrt{2(10)^2 + 2(12)^2 - 4(8)^2}
\]\[
P = 16 + \sqrt{200 + 288 - 256}
\]\[
P = 16 + \sqrt{232} \approx 16 + 15.23 = 31.23 \, \text{cm}
\] - Thus, the perimeter is approximately 31.23 cm.
Example 3: Given Perimeter and One Side
Find the length of the other side of a parallelogram if the perimeter is 48 cm and one side is 16 cm.
- Identify the given values: \(P = 48 \, \text{cm}\), \(a = 16 \, \text{cm}\).
- Use the perimeter formula: \(P = 2(a + b)\).
- Set up the equation:
\[
48 = 2(16 + b)
\] - Solve for \(b\):
\[
48 = 32 + 2b
\]\[
48 - 32 = 2b
\]\[
16 = 2b
\]\[
b = 8 \, \text{cm}
\] - Thus, the length of the other side is 8 cm.
Common Mistakes to Avoid
When calculating the perimeter of a parallelogram, there are several common mistakes that students and practitioners should be aware of to ensure accuracy. Below are the most frequent errors and tips on how to avoid them:
- Using Incorrect Formulas:
Ensure you are using the correct formula for the perimeter of a parallelogram. The standard formula is \( P = 2(a + b) \), where \( a \) and \( b \) are the lengths of the adjacent sides.
- Confusing Perimeter with Area:
Remember that the perimeter is the total distance around the parallelogram, whereas the area is the measure of the space enclosed. Do not confuse the two calculations.
- Neglecting Units:
Always include the units in your final answer. Consistency in units is crucial, as mixing different units can lead to incorrect results.
- Incorrectly Measuring Sides:
Ensure that the lengths of the sides are measured accurately. Misidentifying sides or measuring incorrectly can lead to significant errors in the perimeter calculation.
- Forgetting to Double the Sum of Sides:
Some might forget to multiply the sum of the adjacent sides by 2. The formula \( P = 2(a + b) \) requires doubling the sum of the side lengths.
- Misidentifying Adjacent Sides:
In a parallelogram, opposite sides are equal. Make sure to correctly identify the pairs of adjacent sides to use in the formula.
- Errors in Advanced Formulas:
When using more complex formulas involving diagonals or angles, double-check your steps. For example, with one side and diagonals, use \( P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2} \), and verify each calculation.
By being mindful of these common mistakes, you can improve the accuracy of your calculations and deepen your understanding of the properties of parallelograms.
Applications of Perimeter Calculation
Calculating the perimeter of a parallelogram has numerous practical applications in various fields. Below are some of the key areas where this mathematical skill is particularly useful:
-
Architecture and Construction:
In architecture and construction, knowing the perimeter of a parallelogram is essential for determining the amount of materials needed for building projects, such as fencing, flooring, and wall coverings. Accurate perimeter calculations help in budgeting and ensuring that there is no wastage of materials.
-
Landscaping and Gardening:
Landscapers and gardeners use perimeter calculations to design and lay out garden beds, lawns, and other outdoor spaces. For example, when creating a parallelogram-shaped garden plot, the perimeter helps in determining the length of fencing or edging required.
-
Textile Industry:
In the textile industry, the perimeter of fabric pieces is calculated to determine the amount of material needed for hemming and sewing. This is particularly useful in tailoring and garment manufacturing, where precise measurements are crucial.
-
Graphic Design and Art:
Graphic designers and artists often work with shapes, including parallelograms, when creating digital artwork, patterns, and designs. Knowing the perimeter allows for accurate scaling and positioning within a layout.
-
Engineering:
Engineers use perimeter calculations in various design processes, including the creation of machine parts, components, and structures. For instance, in mechanical engineering, the perimeter of a parallelogram-shaped part might be required to determine the length of material needed for fabrication.
-
Mathematics Education:
Teaching students how to calculate the perimeter of a parallelogram helps in developing their spatial reasoning and problem-solving skills. It provides a practical application of mathematical concepts that can be applied in real-world scenarios.
Advanced Problems and Solutions
The following section explores advanced problems involving the perimeter of a parallelogram. We will address various scenarios and provide step-by-step solutions to deepen your understanding.
Problem 1: Finding the Perimeter with Given Diagonals
Given a parallelogram with sides \( a \) and \( b \), and diagonals \( x \) and \( y \), where \( a \), \( x \), and \( y \) are known. Calculate the perimeter of the parallelogram.
Solution:
- Apply the law of cosines to triangles within the parallelogram:
\[ x^2 = a^2 + b^2 - 2ab \cos(\angle ABC) \]
\[ y^2 = a^2 + b^2 - 2ab \cos(\angle BAD) \]
- Add the equations and simplify:
\[ x^2 + y^2 = 2a^2 + 2b^2 - 2ab(\cos(\angle ABC) + \cos(\angle BAD)) \]
\[ \cos(\angle ABC) = -\cos(\angle BAD) \]
\[ x^2 + y^2 = 2a^2 + 2b^2 \]
\[ 2b^2 = x^2 + y^2 - 2a^2 \]
\[ b = \sqrt{\frac{x^2 + y^2 - 2a^2}{2}} \]
- Calculate the perimeter:
\[ P = 2(a + b) \]
\[ P = 2a + 2 \sqrt{\frac{x^2 + y^2 - 2a^2}{2}} \]
Problem 2: Lengths and Angles in a Parallelogram
Given a parallelogram with sides in the ratio 5:4 and a perimeter of 54 cm, find the lengths of the sides.
Solution:
- Let the sides be \( 5a \) and \( 4a \).
\[ 2(5a + 4a) = 54 \]
\[ 18a = 54 \]
\[ a = 3 \]
- The lengths of the sides are:
\[ 5a = 15 \text{ cm} \]
\[ 4a = 12 \text{ cm} \]
Problem 3: Perimeter Using Trigonometric Ratios
Given the length of side \( AB = 15 \) cm and angle \( \angle D = 45^\circ \), find the height \( h \) and the length of side \( BC \) if the area is 1000 cm².
Solution:
- Calculate the height using the sine function:
\[ \sin(45^\circ) = \frac{h}{15} \]
\[ h = 15 \times \frac{\sqrt{2}}{2} = 10.61 \text{ cm} \]
- Calculate the length of \( BC \) using the area:
\[ \text{Area} = \text{Base} \times \text{Height} \]
\[ 1000 = BC \times 10.61 \]
\[ BC = \frac{1000}{10.61} \approx 94.28 \text{ cm} \]
Problem 4: Finding All Internal Angles
Given a parallelogram with an area of 300 cm², find all internal angles.
Solution:
- Divide the parallelogram into two congruent triangles.
\[ \text{Area of each triangle} = \frac{1}{2} \times \text{Base} \times \text{Height} \times \sin(\theta) \]
\[ 300 = 2 \times \frac{1}{2} \times 30 \times 20 \times \sin(\theta) \]
\[ 300 = 600 \sin(\theta) \]
\[ \sin(\theta) = \frac{1}{2} \]
- Thus, the angles are:
\[ \theta = 30^\circ \] and \[ 150^\circ \]
Frequently Asked Questions
- What is the perimeter of a parallelogram?
The perimeter of a parallelogram is the total distance around the outside of the shape. It is calculated by adding the lengths of all four sides. Since opposite sides of a parallelogram are equal, the formula simplifies to \( P = 2(a + b) \), where \( a \) and \( b \) are the lengths of two adjacent sides.
- How do you find the perimeter of a parallelogram if only the diagonals and one side are given?
In cases where you know one side (\( a \)) and the lengths of the diagonals (\( x \) and \( y \)), the perimeter can be found using the formula:
\( P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2} \)
- Can you determine the perimeter using base, height, and an angle?
Yes, if you know the base (\( b \)), height (\( h \)), and an angle (\( \theta \)), you can use the formula:
\( P = 2b + 2h / \sin(\theta) \)
- What are the units for measuring the perimeter of a parallelogram?
The units for measuring the perimeter are linear, such as centimeters (cm), meters (m), inches (in), feet (ft), or yards (yd).
- Is the perimeter of a parallelogram always equal to the sum of its four sides?
Yes, the perimeter is always the sum of all four sides. For a parallelogram with side lengths \( a \) and \( b \), it is calculated as \( P = 2(a + b) \).
- How is the perimeter of a rectangle different from that of a parallelogram?
While both shapes have opposite sides that are equal, the formula for the perimeter of a rectangle is \( P = 2(a + b) \), where \( a \) is the length and \( b \) is the width. For a parallelogram, the same formula applies, but the sides can form any angle, not just right angles.
- What are some common mistakes to avoid when calculating the perimeter of a parallelogram?
- Not correctly identifying the lengths of the sides.
- Confusing the formula with that of a different shape.
- Forgetting to double the sum of the lengths of the two adjacent sides.
Conclusion
In conclusion, finding the perimeter of a parallelogram is a fundamental aspect of geometry that can be applied in various real-world scenarios. The perimeter is simply the sum of all the sides, which can be calculated using different formulas depending on the given information.
The standard formula for the perimeter of a parallelogram with side lengths \(a\) and \(b\) is:
\[
P = 2(a + b)
\]
In cases where the diagonals or other dimensions are given, alternative formulas such as:
\[
P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2}
\]
or
\[
P = 2a + 2 \frac{h}{\sin \theta}
\]
can be used, providing flexibility and ensuring accurate calculations under various conditions.
Understanding these formulas and their derivations not only aids in solving mathematical problems but also enhances critical thinking and problem-solving skills. These skills are essential for academic success and practical applications in fields such as engineering, architecture, and design, where precise measurements are crucial.
By mastering the calculation of a parallelogram's perimeter, students and professionals can approach related challenges with confidence and accuracy, ensuring their work is both efficient and reliable. The knowledge gained from these calculations extends beyond the classroom, contributing to a deeper appreciation of geometry in everyday life.
With practice and application, the process of finding the perimeter of a parallelogram becomes intuitive, enabling individuals to tackle more complex geometrical problems with ease. Whether for academic purposes, professional use, or personal interest, the principles of calculating perimeters remain a valuable and enduring part of mathematical education.
Video hướng dẫn chi tiết cách tìm diện tích và chu vi hình bình hành, phù hợp với từ khóa 'find the perimeter of a parallelogram'.
Cách Tìm Diện Tích và Chu Vi Hình Bình Hành
READ MORE:
Video hướng dẫn cách tính chu vi hình bình hành, phù hợp với từ khóa 'find the perimeter of a parallelogram'.
Cách Tính Chu Vi Hình Bình Hành