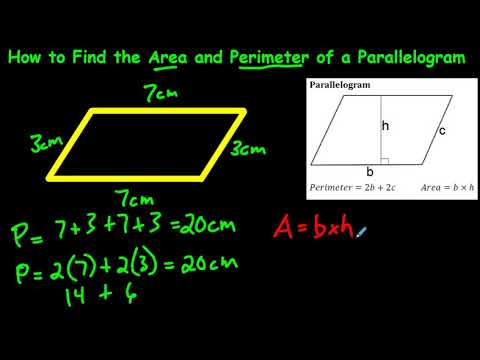
Topic formula for the perimeter of a right triangle: Discover the essential formula for the perimeter of a right triangle in this comprehensive guide. Learn step-by-step methods to calculate the perimeter, explore practical examples, and understand how to avoid common mistakes. Perfect for students, teachers, and math enthusiasts looking to deepen their knowledge of right triangle properties.
Table of Content
- Formula for the Perimeter of a Right Triangle
- Introduction to Right Triangles
- Understanding the Perimeter of a Right Triangle
- Basic Formula for the Perimeter
- Step-by-Step Calculation
- Using the Pythagorean Theorem
- Examples and Practice Problems
- Common Mistakes to Avoid
- Real-Life Applications
- Advanced Topics
- Frequently Asked Questions
- Summary and Conclusion
- YOUTUBE: Khám phá cách tính diện tích và chu vi của tam giác vuông với Thầy J. Hướng dẫn chi tiết và dễ hiểu giúp bạn nắm vững kiến thức cơ bản về hình học.
Formula for the Perimeter of a Right Triangle
The perimeter of a right triangle is the total length of its three sides. A right triangle consists of two legs and a hypotenuse, where the hypotenuse is the longest side opposite the right angle.
Understanding the Formula
The formula to calculate the perimeter \( P \) of a right triangle is:
where:
- is one leg of the triangle
- is the other leg of the triangle
- is the hypotenuse of the triangle
Steps to Calculate the Perimeter
- Identify the lengths of the two legs ( and ).
- Determine the length of the hypotenuse () using the Pythagorean theorem if not given:
Therefore,
- Sum the lengths of all three sides:
Example Calculation
Consider a right triangle with legs units and units. To find the perimeter:
- Calculate the hypotenuse :
- Add the lengths of all sides:
Therefore, the perimeter of the right triangle is 12 units.

READ MORE:
Introduction to Right Triangles
A right triangle, also known as a right-angled triangle, is a type of triangle in which one of the angles is exactly 90 degrees. This distinctive feature makes the right triangle a fundamental concept in geometry and trigonometry, with numerous practical applications.
The primary characteristics of a right triangle include:
- Right Angle: One angle measures 90 degrees.
- Hypotenuse: The side opposite the right angle, which is the longest side of the triangle.
- Legs: The two sides that form the right angle.
Right triangles are classified into two main types based on the lengths of their sides:
- Isosceles Right Triangle: Both legs are of equal length, and the angles opposite these sides are 45 degrees each.
- Scalene Right Triangle: All sides and angles are of different lengths and measures, respectively.
Right triangles are widely used in various fields such as construction, navigation, and physics due to their unique properties. Understanding the properties and formulas associated with right triangles is essential for solving many geometric problems.
In summary, right triangles play a crucial role in both theoretical and applied mathematics. Their simple yet powerful properties make them indispensable tools for solving problems related to angles, distances, and areas.
Understanding the Perimeter of a Right Triangle
The perimeter of a right triangle is the total length around the triangle. To understand the perimeter, it's important to first recall the basic components of a right triangle:
- Hypotenuse (c): The longest side, opposite the right angle.
- Legs (a and b): The two shorter sides that form the right angle.
The formula for the perimeter (P) of a right triangle is given by:
Here, and are the lengths of the legs, and is the length of the hypotenuse. If the lengths of two sides are known, the length of the third side can be calculated using the Pythagorean theorem:
Once the length of all three sides is known, the perimeter can be easily calculated by summing them up.
Let's look at a step-by-step example:
- Consider a right triangle with sides = 5, = 12, and = 13.
- Using the perimeter formula:
- Calculate the sum:
Thus, the perimeter of the triangle is 30 units.
In another example, consider a right triangle where = 8 and = 15. First, find the hypotenuse :
Then,
Finally, calculate the perimeter:
Therefore, the perimeter of the triangle is 40 units.
Understanding how to calculate the perimeter of a right triangle is essential for solving many geometric problems and real-world applications.
Basic Formula for the Perimeter
The perimeter of a right triangle is the sum of the lengths of its three sides. In a right triangle, we have two legs (a and b) and the hypotenuse (c). The basic formula to calculate the perimeter (P) is:
\[ P = a + b + c \]
To find the length of the hypotenuse when only the lengths of the two legs are known, we can use the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} \]
Once we have all three sides, we can easily find the perimeter. Here's a step-by-step approach to calculating the perimeter of a right triangle:
- Identify the lengths of the two legs, \( a \) and \( b \).
- Use the Pythagorean theorem to calculate the hypotenuse \( c \):
- Add the lengths of the three sides to find the perimeter:
\[ c = \sqrt{a^2 + b^2} \]
\[ P = a + b + c \]
Let's look at an example:
Example: Calculate the perimeter of a right triangle with legs of length 3 cm and 4 cm.
- Identify the lengths of the legs: \( a = 3 \) cm and \( b = 4 \) cm.
- Calculate the hypotenuse:
- Find the perimeter:
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \] cm
\[ P = 3 + 4 + 5 = 12 \] cm
Therefore, the perimeter of the right triangle is 12 cm.
This formula and method can be applied to any right triangle to determine its perimeter, as long as the lengths of at least two sides are known.
Step-by-Step Calculation
Calculating the perimeter of a right triangle involves a series of steps, which include identifying the lengths of the sides and applying the Pythagorean theorem where necessary. Here’s a detailed step-by-step guide:
-
Identify the lengths of the sides:
- Base (a)
- Height (b)
- Hypotenuse (c)
-
Calculate the missing side using the Pythagorean theorem (if needed):
If you only know the lengths of the base and height, use the Pythagorean theorem to find the hypotenuse:
\[ c = \sqrt{a^2 + b^2} \]Example:
- Base (\(a\)) = 3 units
- Height (\(b\)) = 4 units
Calculate the hypotenuse (\(c\)):
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{units} \] -
Sum the lengths of all three sides:
The formula for the perimeter (\(P\)) is:
\[ P = a + b + c \]Using the example above with sides 3 units, 4 units, and 5 units:
\[ P = 3 + 4 + 5 = 12 \, \text{units} \]
Let’s look at another example:
-
Given:
- Base (\(a\)) = 6 units
- Height (\(b\)) = 8 units
-
Calculate the hypotenuse (\(c\)):
\[ c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \, \text{units} \] -
Calculate the perimeter (\(P\)):
\[ P = 6 + 8 + 10 = 24 \, \text{units} \]
By following these steps, you can accurately determine the perimeter of any right triangle, whether you start with the lengths of two sides or all three sides.
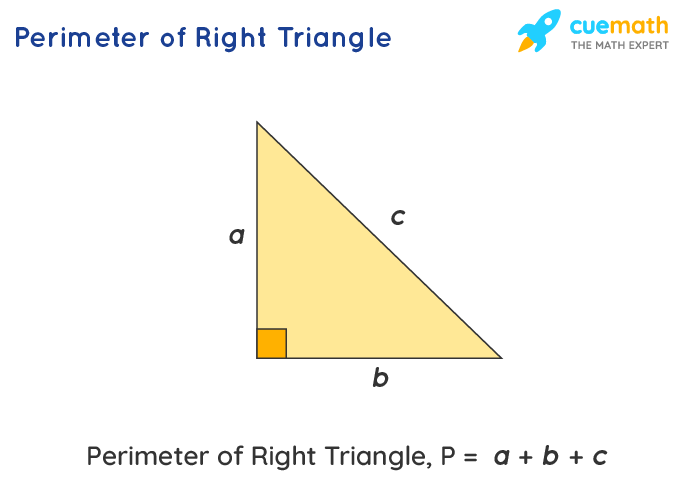
Using the Pythagorean Theorem
The Pythagorean Theorem is a fundamental principle in geometry that relates the lengths of the sides in a right triangle. The theorem states:
\[ c^2 = a^2 + b^2 \]
where:
- c is the length of the hypotenuse (the side opposite the right angle)
- a and b are the lengths of the other two sides
Using the Pythagorean Theorem, we can find the perimeter of a right triangle if we know the lengths of any two sides. The perimeter P is the sum of all three sides:
\[ P = a + b + c \]
Let's go through a step-by-step example:
- Identify the lengths of the two known sides. For instance, let a = 3 and b = 4.
- Use the Pythagorean Theorem to find the length of the hypotenuse c:
- Calculate the perimeter by adding the lengths of all three sides:
\[ c = \sqrt{a^2 + b^2} \]
\[ c = \sqrt{3^2 + 4^2} \]
\[ c = \sqrt{9 + 16} \]
\[ c = \sqrt{25} \]
\[ c = 5 \]
\[ P = a + b + c \]
\[ P = 3 + 4 + 5 \]
\[ P = 12 \]
Therefore, the perimeter of the right triangle with sides 3, 4, and 5 is 12.
This method can be used for any right triangle where the lengths of at least two sides are known. By applying the Pythagorean Theorem, you can determine the length of the missing side and then calculate the perimeter.
Examples and Practice Problems
Understanding the perimeter of a right triangle can be reinforced through various examples and practice problems. Here, we provide step-by-step solutions to common problems involving the calculation of the perimeter.
Example 1
Problem: Find the perimeter of a right triangle with sides of length 8 m, 9 m, and 12.4 m.
Solution:
- Side 1: \(a = 8\) m
- Side 2: \(b = 9\) m
- Hypotenuse: \(c = 12.4\) m
Using the perimeter formula \( P = a + b + c \):
\[
P = 8 + 9 + 12.4 = 29.4 \text{ m}
\]
Example 2
Problem: What is the perimeter of a right triangle with sides 10 m, 24 m, and 26 m?
Solution:
- Side 1: \(a = 10\) m
- Side 2: \(b = 24\) m
- Hypotenuse: \(c = 26\) m
Using the perimeter formula:
\[
P = 10 + 24 + 26 = 60 \text{ m}
\]
Example 3
Problem: Calculate the perimeter of a right triangle with sides 11 cm, 12 cm, and 16.28 cm.
Solution:
- Side 1: \(a = 11\) cm
- Side 2: \(b = 12\) cm
- Hypotenuse: \(c = 16.28\) cm
Using the perimeter formula:
\[
P = 11 + 12 + 16.28 = 39.28 \text{ cm}
\]
Example 4
Problem: What is the perimeter of a right triangle with sides 5 m and 12 m?
Solution:
- Side 1: \(a = 5\) m
- Side 2: \(b = 12\) m
First, find the hypotenuse using the Pythagorean theorem:
\[
c^2 = a^2 + b^2 = 5^2 + 12^2 = 25 + 144 = 169
\]
\[
c = \sqrt{169} = 13 \text{ m}
\]
Using the perimeter formula:
\[
P = 5 + 12 + 13 = 30 \text{ m}
\]
Example 5
Problem: Calculate the perimeter of a right triangle with sides 8 m and 11 m.
Solution:
- Side 1: \(a = 8\) m
- Side 2: \(b = 11\) m
First, find the hypotenuse:
\[
c^2 = a^2 + b^2 = 8^2 + 11^2 = 64 + 121 = 185
\]
\[
c = \sqrt{185} \approx 13.6 \text{ m}
\]
Using the perimeter formula:
\[
P = 8 + 11 + 13.6 = 32.6 \text{ m}
\]
Practice Problems
Test your understanding with these practice problems:
- What is the perimeter of a right triangle with sides 7 m, 9 m, and 11.4 m?
- Calculate the perimeter of a triangle with sides 11 m, 15 m, and 18.6 m.
- A right triangle has sides of lengths 9 m and 12 m. What is the perimeter?
Common Mistakes to Avoid
Calculating the perimeter of a right triangle seems straightforward, but there are common pitfalls that can lead to incorrect results. Being aware of these can help ensure accuracy in your calculations.
- Ignoring the Pythagorean Theorem: Not using the Pythagorean theorem to find the length of the hypotenuse when only the legs are known can result in an incorrect perimeter calculation. The theorem states that \(c = \sqrt{a^2 + b^2}\), where \(a\) and \(b\) are the legs of the triangle.
- Mixing Units: Combining different units of measurement without converting them to a common unit first can lead to errors in the final perimeter. Ensure all side lengths are in the same unit before calculating.
- Rounding Errors: Overly rounding the lengths of sides before the final calculation can significantly affect the accuracy of the perimeter. It's best to keep more decimal places during intermediate steps and round only the final result.
- Forgetting to Add All Sides: A simple but common mistake is forgetting to add all three sides of the triangle when calculating the perimeter. Always use the formula \(P = a + b + c\).
- Incorrect Application of Formulas: Misapplying formulas or using the wrong formula altogether can lead to miscalculations. Double-check which formula is appropriate for the given problem.
Avoiding these mistakes requires careful attention to detail and a thorough understanding of the principles behind the right triangle perimeter calculation.
Real-Life Applications
The formula for the perimeter of a right triangle has numerous practical applications across various fields. Understanding these applications can help illustrate the importance and utility of this mathematical concept.
- Architecture and Construction: Right triangles are used to ensure structures are level and properly aligned. For instance, when constructing buildings, architects and engineers use the Pythagorean theorem to determine the correct lengths and angles to ensure stability and precision.
- Navigation: In maritime and aviation navigation, right triangles help in calculating distances and plotting courses. The Pythagorean theorem assists in determining the shortest path between two points, which is crucial for efficient travel and safety.
- Carpentry: Carpenters frequently use right triangles to create precise cuts and angles. For example, when framing a house, they ensure that corners are square and that walls are straight, which is vital for the integrity of the structure.
- Surveying: Surveyors use right triangles to measure distances and heights indirectly. By using instruments like the theodolite, they can calculate the height of buildings, trees, or other structures from a distance by forming a right triangle with the ground and a sight line.
- Astronomy: Astronomers use right triangles to calculate distances between celestial bodies. By observing angles and applying trigonometric functions, they can determine the relative positions and distances of stars and planets.
- Robotics and Space Exploration: In space missions, robotic arms and other equipment are maneuvered using principles of right triangles. Calculating the correct angles and distances ensures precise movements and placements in the challenging environment of space.
These applications demonstrate how a simple mathematical formula can have far-reaching implications in everyday life and advanced technology. By mastering the perimeter and other properties of right triangles, one can solve a wide array of practical problems.

Advanced Topics
In this section, we will explore some advanced topics related to the perimeter of a right triangle. These topics include the use of trigonometric identities, the relationship between the perimeter and the area, and applications in different fields.
1. Trigonometric Identities and the Perimeter
Trigonometric identities can be used to express the perimeter of a right triangle in terms of its angles. For a right triangle with angle \( \theta \), opposite side \( a \), adjacent side \( b \), and hypotenuse \( c \):
- \( a = c \sin(\theta) \)
- \( b = c \cos(\theta) \)
Thus, the perimeter \( P \) can be written as:
\[
P = a + b + c = c (\sin(\theta) + \cos(\theta) + 1)
\]
2. Relationship Between Perimeter and Area
The area \( A \) of a right triangle can be related to its perimeter. Given sides \( a \), \( b \), and \( c \) with perimeter \( P \):
\[
A = \frac{1}{2} a b
\]
Using the semi-perimeter \( s = \frac{P}{2} \), the area can also be expressed using Heron's formula:
\[
A = \sqrt{s (s-a)(s-b)(s-c)}
\]
This relationship helps in various applications such as optimization problems in engineering and design.
3. Perimeter in Different Coordinate Systems
In analytic geometry, the coordinates of a right triangle's vertices can be used to determine its perimeter. If the vertices are \( (x_1, y_1) \), \( (x_2, y_2) \), and \( (x_3, y_3) \), the lengths of the sides can be calculated using the distance formula:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
Sum these distances to find the perimeter.
4. Perimeter in Practical Applications
Right triangles are frequently used in various fields such as architecture, engineering, and physics. Knowing the perimeter is crucial for material estimations and structural calculations. For example, in truss design, the perimeter determines the amount of material needed for construction.
5. Perimeter in Non-Euclidean Geometry
In non-Euclidean geometry, particularly in spherical and hyperbolic spaces, the concept of the perimeter of a right triangle changes. The sum of the angles of a triangle in these geometries is not equal to 180 degrees, affecting the calculation of the perimeter. Advanced mathematical techniques are used to handle these cases.
6. Exercises and Problems
Practice problems to enhance understanding:
- Given a right triangle with sides 7, 24, and 25 units, calculate its perimeter.
- If the angles of a right triangle are \(30^\circ\) and \(60^\circ\), and the hypotenuse is 10 units, find the perimeter.
- In a right triangle with vertices at (0,0), (3,0), and (0,4), determine the perimeter.
Frequently Asked Questions
- What is the perimeter of a right triangle?
The perimeter of a right triangle is the sum of the lengths of all three sides. If the sides are denoted as \( a \), \( b \), and \( c \) (where \( c \) is the hypotenuse), the perimeter \( P \) is given by:
\[ P = a + b + c \]
- How do you find the perimeter if you know two sides of a right triangle?
If you know the lengths of the two legs \( a \) and \( b \), you can use the Pythagorean theorem to find the hypotenuse \( c \). The Pythagorean theorem states:
\[ c = \sqrt{a^2 + b^2} \]
Once you have \( c \), the perimeter is:
\[ P = a + b + c \]
- What is the formula for the hypotenuse of a right triangle?
The hypotenuse \( c \) of a right triangle can be found using the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} \]
where \( a \) and \( b \) are the lengths of the legs of the triangle.
- How do you calculate the perimeter of a right triangle with an example?
Suppose you have a right triangle with sides \( a = 3 \) units, \( b = 4 \) units, and \( c = 5 \) units. The perimeter \( P \) is calculated as:
\[ P = a + b + c = 3 + 4 + 5 = 12 \] units
- Can the perimeter of a right triangle be a non-integer?
Yes, the perimeter can be a non-integer if the side lengths are not integers. For example, if \( a = 1 \), \( b = 1 \), then \( c = \sqrt{1^2 + 1^2} = \sqrt{2} \). The perimeter is:
\[ P = 1 + 1 + \sqrt{2} \approx 3.414 \]
- What units are used to measure the perimeter of a right triangle?
The units for the perimeter of a right triangle are the same as the units used for the side lengths. These can be any unit of length such as meters, centimeters, feet, or inches.
- How is the perimeter of an isosceles right triangle different from other right triangles?
In an isosceles right triangle, the two legs are equal. If the length of each leg is \( a \), then the hypotenuse \( c \) is:
\[ c = a\sqrt{2} \]
The perimeter \( P \) is:
\[ P = a + a + a\sqrt{2} = 2a + a\sqrt{2} = a(2 + \sqrt{2}) \]
- Are there any practical applications for calculating the perimeter of right triangles?
Yes, calculating the perimeter of right triangles is useful in various real-life scenarios such as construction, navigation, and design. For example, determining the amount of material needed to build a triangular garden or the distance around a triangular plot of land.
Summary and Conclusion
Understanding the perimeter of a right triangle involves using simple mathematical concepts and formulas that are fundamental in geometry and trigonometry. The perimeter is the total distance around the triangle, calculated by adding the lengths of its three sides.
The formula for the perimeter \( P \) of a right triangle with sides \( a \), \( b \), and hypotenuse \( c \) is given by:
\[ P = a + b + c \]
To summarize:
- The perimeter of a right triangle is found by summing the lengths of all three sides.
- The Pythagorean theorem helps in finding the length of the hypotenuse if the lengths of the other two sides are known: \[ c^2 = a^2 + b^2 \]
- In practical applications, knowing how to calculate the perimeter helps in fields such as construction, navigation, and various design projects where right triangles are commonly used.
In conclusion, mastering the calculation of the perimeter of a right triangle is essential for solving a wide range of mathematical problems and real-world applications. This knowledge not only reinforces the understanding of basic geometric principles but also builds a foundation for more advanced mathematical concepts.
Keep practicing and exploring the properties of right triangles, as they are fundamental shapes that appear frequently in both academic studies and everyday life. By continually applying these concepts, you will enhance your mathematical skills and problem-solving abilities.
Khám phá cách tính diện tích và chu vi của tam giác vuông với Thầy J. Hướng dẫn chi tiết và dễ hiểu giúp bạn nắm vững kiến thức cơ bản về hình học.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán với Thầy J
READ MORE:
Hướng dẫn chi tiết cách tính diện tích và chu vi của tam giác vuông. Video giúp bạn nắm vững kiến thức cơ bản và áp dụng vào bài toán thực tế.
Cách Tìm Diện Tích và Chu Vi của Tam Giác Vuông