Topic how to find perimeter of a polygon: Learn how to find the perimeter of a polygon with our comprehensive guide. Whether you are dealing with regular or irregular polygons, our step-by-step instructions and practical examples will make the process simple and easy to understand. Discover the formulas and techniques needed to calculate the perimeter accurately for any polygon.
Table of Content
- How to Find the Perimeter of a Polygon
- Introduction to Perimeter
- Definition of a Polygon
- Types of Polygons
- Understanding Perimeter
- Perimeter of Regular Polygons
- Perimeter of Irregular Polygons
- Perimeter Calculation Methods
- Formulas for Common Polygons
- Step-by-Step Calculation
- Practical Examples
- Applications of Perimeter
- Common Mistakes to Avoid
- Practice Problems
- Visualizing Perimeter
- Advanced Perimeter Concepts
- Conclusion
- YOUTUBE:
How to Find the Perimeter of a Polygon
The perimeter of a polygon is the total distance around the outside of the polygon. To find the perimeter, you need to add up the lengths of all the sides. Here are the steps to calculate the perimeter for different types of polygons:
Regular Polygon
A regular polygon has all sides of equal length. The formula for finding the perimeter of a regular polygon is:
\[
\text{Perimeter} = \text{number of sides} \times \text{length of one side}
\]
For example, to find the perimeter of a regular hexagon with each side measuring 6 units:
\[
\text{Perimeter} = 6 \times 6 = 36 \, \text{units}
\]
Irregular Polygon
An irregular polygon has sides of different lengths. To find the perimeter of an irregular polygon, you need to add the lengths of all the sides together:
\[
\text{Perimeter} = a + b + c + d + \ldots
\]
For example, if an irregular polygon has sides measuring 3 units, 4 units, 5 units, and 6 units:
\[
\text{Perimeter} = 3 + 4 + 5 + 6 = 18 \, \text{units}
\]
Special Cases
- Triangle: For a triangle, add the lengths of the three sides. \[ \text{Perimeter} = a + b + c \]
- Rectangle: For a rectangle, add the lengths of the four sides, or use the formula: \[ \text{Perimeter} = 2 \times (\text{length} + \text{width}) \]
- Square: For a square, since all sides are equal, the formula is: \[ \text{Perimeter} = 4 \times \text{side length} \]
Example Calculations
- Regular Pentagon: Each side is 5 units.
\[
\text{Perimeter} = 5 \times 5 = 25 \, \text{units}
\] - Irregular Quadrilateral: Sides are 2 units, 3 units, 4 units, and 5 units.
\[
\text{Perimeter} = 2 + 3 + 4 + 5 = 14 \, \text{units}
\]
Visual Representation
For visual learners, it might help to draw the polygon and label each side with its length. Then, simply add the numbers together to find the total perimeter.
By following these methods, you can easily calculate the perimeter of any polygon, whether it is regular or irregular.

READ MORE:
Introduction to Perimeter
The perimeter of a polygon is the total length around the outside of the shape. It is a measure of the distance that encloses the polygon. Understanding the perimeter is crucial for various practical applications, including construction, land measurement, and design. Here, we will explain the concept of the perimeter and how to calculate it for different types of polygons.
The general steps to find the perimeter of a polygon are:
- Identify the Polygon Type: Determine whether the polygon is regular (all sides and angles are equal) or irregular (sides and angles are different).
- Measure the Sides: Measure the length of each side of the polygon. For regular polygons, measuring one side is sufficient.
- Apply the Formula: Use the appropriate formula based on the type of polygon.
For regular polygons, the formula to find the perimeter is:
\[
\text{Perimeter} = \text{number of sides} \times \text{length of one side}
\]
For irregular polygons, the perimeter is the sum of the lengths of all the sides:
\[
\text{Perimeter} = a + b + c + d + \ldots
\]
Let's look at examples to clarify these concepts:
- Example 1: A regular pentagon with each side measuring 4 units.
\[
\text{Perimeter} = 5 \times 4 = 20 \, \text{units}
\] - Example 2: An irregular quadrilateral with sides measuring 3 units, 4 units, 5 units, and 6 units.
\[
\text{Perimeter} = 3 + 4 + 5 + 6 = 18 \, \text{units}
\]
By following these steps and using the appropriate formulas, you can easily calculate the perimeter of any polygon, ensuring accuracy and understanding in various practical situations.
Definition of a Polygon
A polygon is a two-dimensional geometric figure with a finite number of straight sides that are connected to form a closed shape. The sides are called edges or line segments, and the points where two sides meet are called vertices (singular: vertex). Polygons are an essential concept in geometry and can be classified based on various properties.
Key characteristics of polygons include:
- Sides: The line segments that make up the polygon. Polygons can have any number of sides, with the minimum being three.
- Vertices: The points where two sides of a polygon meet.
- Angles: The space between two intersecting sides. The sum of the interior angles depends on the number of sides.
Polygons are classified based on the number of sides:
- Triangle: A polygon with three sides.
- Quadrilateral: A polygon with four sides.
- Pentagon: A polygon with five sides.
- Hexagon: A polygon with six sides.
- Heptagon: A polygon with seven sides.
- Octagon: A polygon with eight sides.
- Nonagon: A polygon with nine sides.
- Decagon: A polygon with ten sides.
Polygons can also be categorized as regular or irregular:
- Regular Polygon: All sides and angles are equal. For example, an equilateral triangle or a square.
- Irregular Polygon: Sides and angles are not equal. For example, a scalene triangle or a general quadrilateral.
The general properties of polygons include:
- Convex Polygon: All interior angles are less than 180 degrees, and no sides bend inward.
- Concave Polygon: At least one interior angle is greater than 180 degrees, and some sides bend inward.
Understanding the definition and properties of polygons is fundamental in geometry, as it lays the groundwork for more advanced topics and applications, including the calculation of the perimeter.
Types of Polygons
Polygons are classified based on various characteristics, including the number of sides, length of sides, and internal angles. Understanding the different types of polygons is essential for calculating their properties, such as the perimeter and area. Here, we outline the main types of polygons:
Based on the Number of Sides
- Triangle: A polygon with three sides and three vertices.
- Equilateral Triangle: All sides and angles are equal.
- Isosceles Triangle: Two sides and two angles are equal.
- Scalene Triangle: All sides and angles are different.
- Quadrilateral: A polygon with four sides and four vertices.
- Square: All sides and angles are equal.
- Rectangle: Opposite sides are equal, and all angles are 90 degrees.
- Rhombus: All sides are equal, but angles are not 90 degrees.
- Trapezoid: Only one pair of opposite sides is parallel.
- Pentagon: A polygon with five sides and five vertices.
- Hexagon: A polygon with six sides and six vertices.
- Heptagon: A polygon with seven sides and seven vertices.
- Octagon: A polygon with eight sides and eight vertices.
- Nonagon: A polygon with nine sides and nine vertices.
- Decagon: A polygon with ten sides and ten vertices.
Based on Side Lengths and Angles
- Regular Polygon: All sides and angles are equal. Examples include the equilateral triangle and the square.
- Irregular Polygon: Sides and angles are not all equal. Examples include a scalene triangle and a general quadrilateral.
Based on Convexity
- Convex Polygon: All interior angles are less than 180 degrees, and no sides bend inward. Examples include regular polygons and many irregular polygons.
- Concave Polygon: At least one interior angle is greater than 180 degrees, and some sides bend inward. Examples include star-shaped polygons.
Special Polygons
- Equilateral Polygon: All sides are of equal length, but angles may vary. Examples include the rhombus and the equilateral triangle.
- Equiangular Polygon: All angles are equal, but sides may vary in length. Examples include the rectangle and the equiangular hexagon.
Understanding the different types of polygons and their properties is crucial for various applications in mathematics, science, and engineering. This knowledge aids in the accurate calculation of geometric properties, including the perimeter, which is fundamental for solving complex problems.
Understanding Perimeter
The perimeter of a polygon is the total distance around the outside of the shape. It is a crucial measurement in geometry and has various practical applications in fields such as construction, land surveying, and architecture. Understanding how to calculate the perimeter is essential for solving many real-world problems.
Here are the key steps to understand and calculate the perimeter of a polygon:
Step 1: Identify the Polygon Type
First, determine whether the polygon is regular or irregular:
- Regular Polygon: All sides and angles are equal.
- Irregular Polygon: Sides and angles are not all equal.
Step 2: Measure the Length of Each Side
To find the perimeter, you need the lengths of all the sides. For regular polygons, measuring one side is sufficient as all sides are equal. For irregular polygons, measure each side individually.
Step 3: Apply the Appropriate Formula
The formula to calculate the perimeter depends on the type of polygon:
- Regular Polygon: Use the formula:
\[
\text{Perimeter} = \text{number of sides} \times \text{length of one side}
\] - Irregular Polygon: Add the lengths of all the sides:
\[
\text{Perimeter} = a + b + c + d + \ldots
\]
Example Calculations
- Example 1: A regular hexagon with each side measuring 6 units.
\[
\text{Perimeter} = 6 \times 6 = 36 \, \text{units}
\] - Example 2: An irregular pentagon with sides measuring 3 units, 4 units, 5 units, 6 units, and 7 units.
\[
\text{Perimeter} = 3 + 4 + 5 + 6 + 7 = 25 \, \text{units}
\]
Applications of Perimeter
Knowing how to calculate the perimeter is useful in various situations:
- Construction: Determining the amount of materials needed for the boundary of a structure.
- Land Surveying: Measuring the boundary length of a piece of land.
- Architecture: Designing the outlines of buildings and other structures.
By following these steps and understanding the underlying principles, you can accurately calculate the perimeter of any polygon, ensuring precision in both academic and practical applications.
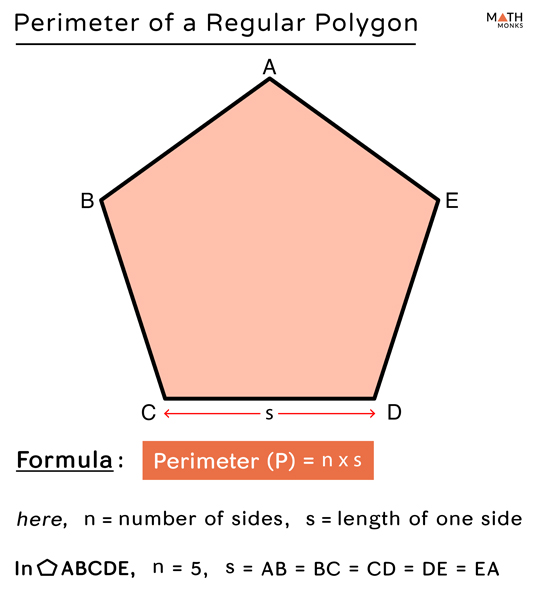
Perimeter of Regular Polygons
A regular polygon is a polygon with all sides and angles equal. Calculating the perimeter of a regular polygon is straightforward due to its uniformity. The perimeter is simply the total length around the polygon, which can be found using a specific formula.
Step-by-Step Calculation
Follow these steps to find the perimeter of a regular polygon:
Step 1: Identify the Number of Sides
Determine the number of sides (\(n\)) of the regular polygon. Common examples include:
- Triangle: 3 sides
- Square: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
Step 2: Measure the Length of One Side
Measure the length (\(s\)) of one side of the polygon. Since the polygon is regular, all sides are of equal length.
Step 3: Apply the Perimeter Formula
Use the formula for the perimeter (\(P\)) of a regular polygon:
\[
P = n \times s
\]
Where \(n\) is the number of sides and \(s\) is the length of one side.
Example Calculations
- Example 1: A regular triangle (equilateral) with each side measuring 5 units.
\[
P = 3 \times 5 = 15 \, \text{units}
\] - Example 2: A regular hexagon with each side measuring 7 units.
\[
P = 6 \times 7 = 42 \, \text{units}
\]
Applications of Perimeter in Regular Polygons
Knowing the perimeter of regular polygons is useful in various contexts:
- Design and Architecture: Calculating the materials needed for constructing objects like frames, tiles, and other geometric designs.
- Landscaping: Planning the layout and boundary of gardens, parks, and other outdoor areas.
- Mathematical Problems: Solving geometry problems in academic settings that require understanding of regular polygons and their properties.
Understanding and calculating the perimeter of regular polygons is a fundamental skill in geometry. By following the simple steps outlined, you can easily determine the perimeter and apply this knowledge to various practical and theoretical situations.
Perimeter of Irregular Polygons
An irregular polygon is a polygon with sides and angles of different lengths and measures. Calculating the perimeter of an irregular polygon involves summing the lengths of all its sides. This process is simple but requires accurate measurement of each side.
Step-by-Step Calculation
Follow these steps to find the perimeter of an irregular polygon:
Step 1: Measure the Length of Each Side
Use a ruler or measuring tool to measure the length of each side of the polygon. Ensure that each measurement is accurate and in the same unit.
Step 2: List the Lengths
Write down the lengths of all the sides. For example, if the polygon has sides of lengths \(a\), \(b\), \(c\), and \(d\), list these values.
Step 3: Sum the Lengths
Add the lengths of all the sides to find the perimeter (\(P\)). Use the formula:
\[
P = a + b + c + d + \ldots
\]
Example Calculations
- Example 1: An irregular quadrilateral with sides measuring 4 units, 5 units, 6 units, and 7 units.
\[
P = 4 + 5 + 6 + 7 = 22 \, \text{units}
\] - Example 2: An irregular pentagon with sides measuring 3 units, 4 units, 5 units, 6 units, and 8 units.
\[
P = 3 + 4 + 5 + 6 + 8 = 26 \, \text{units}
\]
Applications of Perimeter in Irregular Polygons
Knowing the perimeter of irregular polygons is useful in various contexts:
- Construction and Engineering: Determining the materials needed for building irregularly shaped structures and surfaces.
- Land Surveying: Measuring the boundary length of irregular plots of land.
- Art and Design: Creating irregularly shaped designs and artworks where precise boundary measurement is required.
Calculating the perimeter of irregular polygons involves straightforward addition but requires careful measurement. By following these steps and understanding the principles, you can accurately determine the perimeter of any irregular polygon, aiding in various practical and theoretical applications.
Perimeter Calculation Methods
Calculating the perimeter of a polygon depends on whether the polygon is regular or irregular. Here, we outline methods for both types:
Regular Polygons
A regular polygon has all sides and angles equal. The perimeter (P) can be calculated using the formula:
\[
P = n \times s
\]
where \( n \) is the number of sides and \( s \) is the length of one side.
- Identify the number of sides (n) of the polygon.
- Measure the length of one side (s).
- Multiply the number of sides by the length of one side.
For example, for a regular hexagon with each side measuring 5 units:
\[
P = 6 \times 5 = 30 \text{ units}
\]
Irregular Polygons
An irregular polygon has sides of different lengths. The perimeter (P) is the sum of the lengths of all its sides:
\[
P = s_1 + s_2 + s_3 + \ldots + s_n
\]
where \( s_i \) is the length of each side.
- Identify the lengths of all sides of the polygon.
- Add the lengths of all the sides together.
For example, for an irregular quadrilateral with sides measuring 4, 7, 3, and 6 units:
\[
P = 4 + 7 + 3 + 6 = 20 \text{ units}
\]
Using Coordinates
For polygons with vertices at given coordinates, use the distance formula to find the length of each side and then sum them up. If the vertices are \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\), the distance between two points \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\) is:
\[
d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2}
\]
To find the perimeter:
- Calculate the distance between each pair of consecutive vertices.
- Sum all the calculated distances.
For example, for a triangle with vertices at \((0,0), (3,0), (3,4)\):
- Distance between \((0,0)\) and \((3,0)\): \( d_1 = \sqrt{(3-0)^2 + (0-0)^2} = 3 \) units
- Distance between \((3,0)\) and \((3,4)\): \( d_2 = \sqrt{(3-3)^2 + (4-0)^2} = 4 \) units
- Distance between \((3,4)\) and \((0,0)\): \( d_3 = \sqrt{(0-3)^2 + (0-4)^2} = 5 \) units
Total perimeter:
\[
P = d_1 + d_2 + d_3 = 3 + 4 + 5 = 12 \text{ units}
\]
Formulas for Common Polygons
Understanding the formulas for the perimeter of various common polygons is essential for solving many geometric problems. Below are the formulas for some of the most frequently encountered polygons:
Triangle
The perimeter of a triangle is the sum of its three sides:
\[ P = a + b + c \]
Rectangle
The perimeter of a rectangle, with length \( l \) and width \( w \), is calculated as:
\[ P = 2l + 2w \]
Square
A square has all sides equal, so if each side is \( s \), the perimeter is:
\[ P = 4s \]
Parallelogram
The perimeter of a parallelogram, with sides \( a \) and \( b \), is:
\[ P = 2a + 2b \]
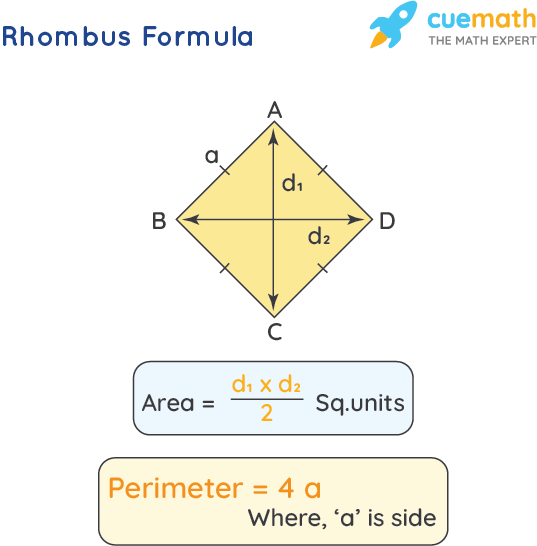
Rhombus
Since all sides of a rhombus are equal, if each side is \( s \), the perimeter is:
\[ P = 4s \]
Trapezoid
For a trapezoid with sides \( a \), \( b \), \( c \), and \( d \), the perimeter is:
\[ P = a + b + c + d \]
Regular Polygon
A regular polygon has all sides equal. If the polygon has \( n \) sides, each of length \( s \), the perimeter is:
\[ P = n \times s \]
Irregular Polygon
The perimeter of an irregular polygon, where the sides are not necessarily equal, is found by summing the lengths of all its sides:
\[ P = a_1 + a_2 + a_3 + \ldots + a_n \]
Examples
- Regular Hexagon: For a hexagon with side length \( s = 6 \) cm:
\[ P = 6 \times 6 = 36 \text{ cm} \]
- Rectangle: For a rectangle with length \( l = 10 \) cm and width \( w = 5 \) cm:
\[ P = 2(10) + 2(5) = 20 + 10 = 30 \text{ cm} \]
- Irregular Quadrilateral: For an irregular quadrilateral with side lengths \( 4 \) cm, \( 5 \) cm, \( 7 \) cm, and \( 6 \) cm:
\[ P = 4 + 5 + 7 + 6 = 22 \text{ cm} \]
By using these formulas, you can quickly determine the perimeter of most common polygons encountered in geometry problems.

Step-by-Step Calculation
Finding the perimeter of a polygon involves adding the lengths of all its sides. The approach can vary slightly depending on whether the polygon is regular or irregular. Below are detailed steps for both scenarios:
Step-by-Step Calculation for Regular Polygons
A regular polygon has all sides of equal length. Here's how to calculate its perimeter:
- Identify the number of sides (\(n\)) of the polygon.
- Measure the length of one side (\(s\)).
- Use the formula: \[ \text{Perimeter} = n \times s \]
- Multiply the number of sides by the length of one side to find the perimeter.
For example, to find the perimeter of a regular hexagon with each side measuring 5 cm:
\[
\text{Perimeter} = 6 \times 5 = 30 \text{ cm}
\]
Step-by-Step Calculation for Irregular Polygons
An irregular polygon has sides of different lengths. Here's how to calculate its perimeter:
- Identify and measure the length of each side.
- List the lengths of all sides.
- Use the formula: \[ \text{Perimeter} = \text{sum of all side lengths} \]
- Add the lengths of all sides to find the perimeter.
For example, to find the perimeter of an irregular polygon with sides measuring 3 cm, 4 cm, 5 cm, and 6 cm:
\[
\text{Perimeter} = 3 + 4 + 5 + 6 = 18 \text{ cm}
\]
Example Calculations
- Square: A square has four equal sides. If one side is 4 meters: \[ \text{Perimeter} = 4 \times 4 = 16 \text{ meters} \]
- Rectangle: A rectangle has opposite sides of equal length. For a rectangle with length 8 meters and width 3 meters: \[ \text{Perimeter} = 2 \times (8 + 3) = 2 \times 11 = 22 \text{ meters} \]
- Triangle: For a triangle with sides 5 meters, 6 meters, and 7 meters: \[ \text{Perimeter} = 5 + 6 + 7 = 18 \text{ meters} \]
- Pentagon: For a regular pentagon with each side 4 meters: \[ \text{Perimeter} = 5 \times 4 = 20 \text{ meters} \]
- Irregular Polygon: For an irregular polygon with sides 3 meters, 5 meters, 7 meters, and 9 meters: \[ \text{Perimeter} = 3 + 5 + 7 + 9 = 24 \text{ meters} \]
Using these steps, you can accurately calculate the perimeter of any polygon, whether regular or irregular.
Practical Examples
Here are some practical examples to help you understand how to find the perimeter of different types of polygons:
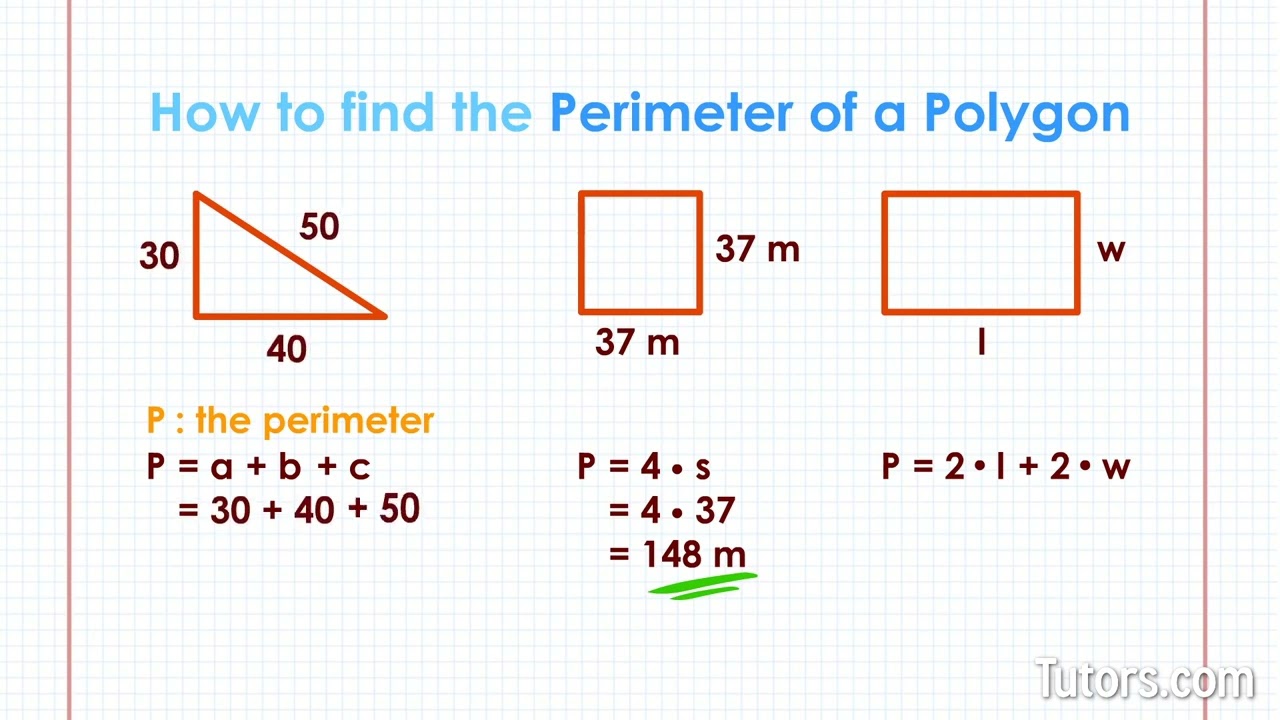
Example 1: Perimeter of a Rectangle
Consider a rectangle with a length of 8 units and a width of 5 units. To find the perimeter, add the lengths of all the sides:
- Length = 8 units
- Width = 5 units
Using the formula for the perimeter of a rectangle:
\( P = 2 \times (\text{length} + \text{width}) \)
\( P = 2 \times (8 + 5) = 2 \times 13 = 26 \) units
Example 2: Perimeter of a Regular Pentagon
Consider a regular pentagon with each side measuring 4 cm. Since all sides are equal, use the formula for the perimeter of a regular polygon:
- Number of sides = 5
- Length of one side = 4 cm
Using the formula for the perimeter:
\( P = \text{number of sides} \times \text{length of one side} \)
\( P = 5 \times 4 = 20 \) cm
Example 3: Perimeter of an Irregular Polygon
Consider an irregular polygon with sides of lengths 7 feet, 9 feet, 6 feet, and 5 feet. To find the perimeter, add the lengths of all the sides:
- Side 1 = 7 feet
- Side 2 = 9 feet
- Side 3 = 6 feet
- Side 4 = 5 feet
The perimeter is:
\( P = 7 + 9 + 6 + 5 = 27 \) feet
Example 4: Perimeter of a Regular Hexagon
Consider a regular hexagon with each side measuring 3 inches. Since all sides are equal, use the formula for the perimeter of a regular polygon:
- Number of sides = 6
- Length of one side = 3 inches
Using the formula for the perimeter:
\( P = \text{number of sides} \times \text{length of one side} \)
\( P = 6 \times 3 = 18 \) inches
Example 5: Perimeter of an Irregular Quadrilateral
Consider an irregular quadrilateral with sides of lengths 5 units, 10 units, 8 units, and 12 units. To find the perimeter, add the lengths of all the sides:
- Side 1 = 5 units
- Side 2 = 10 units
- Side 3 = 8 units
- Side 4 = 12 units
The perimeter is:
\( P = 5 + 10 + 8 + 12 = 35 \) units
Example 6: Perimeter of a Regular Octagon
Consider a regular octagon with each side measuring 2 feet. Since all sides are equal, use the formula for the perimeter of a regular polygon:
- Number of sides = 8
- Length of one side = 2 feet
Using the formula for the perimeter:
\( P = \text{number of sides} \times \text{length of one side} \)
\( P = 8 \times 2 = 16 \) feet
These examples illustrate how to calculate the perimeter for various types of polygons, both regular and irregular. By following these steps and using the appropriate formulas, you can easily find the perimeter of any polygon.
Applications of Perimeter
The concept of perimeter is essential in various practical applications across different fields. Understanding how to calculate and use the perimeter can help solve real-world problems effectively. Here are some of the key applications of perimeter:
-
Architecture and Construction:
Architects and builders use the perimeter to determine the boundaries of a plot of land, the length of fencing required, and the total length of materials needed for construction projects. This helps in accurate planning and budgeting for materials.
-
Landscaping:
Landscapers need to calculate the perimeter to design and layout gardens, pathways, and outdoor spaces. Knowing the perimeter helps in estimating the amount of edging, fencing, or other border materials required.
-
Fencing and Security:
To secure a property, it is crucial to know the perimeter to install appropriate fencing or security barriers. This ensures complete coverage of the area to be protected.
-
Sports Fields:
In sports, the perimeter is used to define the boundaries of fields and courts. For example, the perimeter of a soccer field or a basketball court determines the playing area and helps in marking lines accurately.
-
Fabrication and Manufacturing:
Manufacturers use perimeter calculations in the fabrication of materials such as sheet metal, fabric, and glass. Knowing the perimeter helps in cutting materials to the correct size and minimizing waste.
-
Urban Planning:
Urban planners use the perimeter to design city blocks, parks, and other public spaces. Accurate perimeter measurements are essential for efficient space utilization and infrastructure development.
-
Interior Design:
Interior designers use the perimeter to plan the layout of rooms, including furniture placement and the amount of trim, molding, or baseboard needed. This helps in creating aesthetically pleasing and functional spaces.
-
Education:
Teaching perimeter helps students understand spatial relationships and geometry. It also provides practical problem-solving skills that can be applied in various real-life situations.
These applications highlight the importance of understanding perimeter calculations in various domains. Whether it is for designing, building, securing, or educating, knowing how to find and use the perimeter is a valuable skill.
Common Mistakes to Avoid
Calculating the perimeter of a polygon can seem straightforward, but there are common mistakes that can lead to incorrect results. Here are some key mistakes to watch out for and how to avoid them:
- Incorrect Measurement Units: Ensure all side lengths are measured in the same units. Mixing units (e.g., meters and centimeters) without proper conversion can result in errors.
- Omitting Sides: Make sure to include all sides in the calculation. This is especially important for irregular polygons where sides may not be immediately obvious.
- Incorrect Application of Formulas: Use the appropriate formula for the type of polygon. For example, the formula for a regular polygon is different from that of an irregular polygon.
- Assuming Regularity: Do not assume a polygon is regular (all sides and angles are equal) unless specified. Irregular polygons require individual side measurements.
- Ignoring Precision: Be precise with measurements. Small errors in measurement can add up, especially in polygons with many sides.
- Misidentifying the Shape: Correctly identify the shape of the polygon. The perimeter formula for a rectangle is different from that of a trapezoid.
By being aware of these common mistakes and taking steps to avoid them, you can ensure accurate perimeter calculations for any polygon.

Practice Problems
Below are some practice problems to help reinforce the concepts of finding the perimeter of various polygons. These problems range from basic to advanced, covering both regular and irregular polygons.
-
Problem 1: Perimeter of a Rectangle
Find the perimeter of a rectangle whose length is 14 inches and width is 5 inches.
Solution:
Perimeter = \(2 \times (length + width)\)
Perimeter = \(2 \times (14 + 5) = 2 \times 19 = 38\) inches
-
Problem 2: Perimeter of a Triangle
The sides of a triangle are 6 cm, 8 cm, and 10 cm. Calculate its perimeter.
Solution:
Perimeter = \(6 + 8 + 10 = 24\) cm
-
Problem 3: Perimeter of a Regular Hexagon
If each side of a regular hexagon is 9 feet, find its perimeter.
Solution:
Perimeter = \(6 \times side\)
Perimeter = \(6 \times 9 = 54\) feet
-
Problem 4: Perimeter of an Irregular Polygon
The sides of an irregular pentagon are 3 m, 5 m, 7 m, 4 m, and 6 m. Determine its perimeter.
Solution:
Perimeter = \(3 + 5 + 7 + 4 + 6 = 25\) meters
-
Problem 5: Perimeter Using Coordinates
Find the perimeter of a polygon with vertices at coordinates A(2, 3), B(5, 3), C(5, 7), and D(2, 7).
Solution:
\(AB = \sqrt{(5 - 2)^2 + (3 - 3)^2} = \sqrt{9} = 3\) units
\(BC = \sqrt{(5 - 5)^2 + (7 - 3)^2} = \sqrt{16} = 4\) units
\(CD = \sqrt{(5 - 2)^2 + (7 - 7)^2} = \sqrt{9} = 3\) units
\(DA = \sqrt{(2 - 2)^2 + (7 - 3)^2} = \sqrt{16} = 4\) units
Perimeter = \(3 + 4 + 3 + 4 = 14\) units
-
Problem 6: Finding a Missing Side
The perimeter of a quadrilateral is 50 units. Three of its sides are 12 units, 15 units, and 8 units. Find the length of the fourth side.
Solution:
Let the fourth side be \(x\).
Perimeter = \(12 + 15 + 8 + x = 50\)
\(35 + x = 50\)
\(x = 50 - 35 = 15\) units
These practice problems are designed to help you master the calculation of perimeters for various types of polygons. Practice regularly to improve your skills!
Visualizing Perimeter
Visualizing the perimeter of a polygon helps in understanding the concept better. Here are some methods to visualize and grasp the perimeter of various polygons:
Using Graph Paper
Graph paper is an excellent tool for visualizing the perimeter. By drawing the polygon on graph paper, you can easily measure the length of each side and sum them to find the perimeter.
- Draw the polygon on graph paper, ensuring each vertex is at the intersection of the lines.
- Count the units along each side of the polygon.
- Add the lengths of all sides to find the perimeter.
Interactive Tools
Several online tools and apps allow you to create and manipulate polygons to see how the perimeter changes. For example, you can use:
- - Drag vertices of polygons to see real-time perimeter calculations.
- - Interactive tutorials on calculating perimeters.
Using Physical Objects
Using physical objects like strings or sticks can help visualize the perimeter:
- Arrange the objects to form the shape of the polygon.
- Measure the length of each object.
- Add these lengths to find the perimeter.
Example: Visualizing a Triangle
Consider a triangle with sides 3 cm, 4 cm, and 5 cm.
- Draw the triangle on graph paper or create it using sticks.
- Measure each side: 3 cm, 4 cm, and 5 cm.
- Add the lengths: \(3 + 4 + 5 = 12\) cm.
- The perimeter is 12 cm.
Example: Regular Polygon
For a regular hexagon with each side of 6 cm:
- Draw the hexagon on graph paper.
- Measure one side: 6 cm.
- Since all sides are equal, multiply the length of one side by the number of sides: \(6 \times 6 = 36\) cm.
- The perimeter is 36 cm.
Using these methods, you can effectively visualize and calculate the perimeter of any polygon.
Advanced Perimeter Concepts
Understanding the perimeter of polygons at an advanced level involves exploring more complex concepts and applications. Here, we will discuss several advanced topics related to the perimeter of polygons, including coordinate geometry methods, weighted perimeters, and applications in various fields.
1. Perimeter in Coordinate Geometry
When dealing with polygons on the coordinate plane, we can use the distance formula to find the perimeter. For a polygon with vertices at \((x_1, y_1)\), \((x_2, y_2)\), ..., \((x_n, y_n)\), the perimeter can be calculated by summing the distances between consecutive vertices.
The distance between two points \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\) is given by:
\[
d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2}
\]
Thus, the perimeter \(P\) of the polygon is:
\[
P = \sum_{i=1}^{n-1} \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} + \sqrt{(x_n - x_1)^2 + (y_n - y_1)^2}
\]
2. Weighted Perimeters
In certain applications, edges of a polygon may be assigned different weights or costs. The weighted perimeter is the sum of these weighted lengths. This concept is particularly useful in fields like network design and transportation planning, where different segments may have different traversal costs.
For a polygon with side lengths \(l_1, l_2, ..., l_n\) and corresponding weights \(w_1, w_2, ..., w_n\), the weighted perimeter \(P_w\) is calculated as:
\[
P_w = \sum_{i=1}^n l_i \cdot w_i
\]
3. Perimeter and Optimization Problems
Optimization problems often involve finding the minimum or maximum perimeter under given constraints. For example, finding the maximum area of a polygon with a fixed perimeter is a classic optimization problem, leading to the conclusion that a regular polygon (or a circle in the continuous case) has the largest area for a given perimeter.
In mathematical terms, this involves using calculus of variations and Lagrange multipliers to optimize the perimeter function under given constraints.
4. Fractal Perimeters
Fractals are complex geometric shapes that exhibit self-similarity at various scales. Calculating the perimeter of fractal shapes, such as the Koch snowflake, involves dealing with infinite sums. The perimeter of a fractal increases indefinitely as the shape is iteratively refined.
For example, the perimeter \(P\) of the Koch snowflake after \(n\) iterations is given by:
\[
P = P_0 \left(\frac{4}{3}\right)^n
\]
where \(P_0\) is the initial perimeter of the base equilateral triangle.
5. Applications in Computer Graphics
In computer graphics, the perimeter of polygons is essential for rendering and collision detection. Algorithms like the marching squares and ray-casting rely on perimeter calculations to determine the edges of shapes and their interactions with other objects in a scene.
Efficient computation of polygon perimeters allows for real-time graphics rendering and accurate physical simulations in virtual environments.
Understanding these advanced concepts of perimeter not only enhances theoretical knowledge but also broadens the scope of practical applications in various scientific and engineering fields.
Conclusion
In this comprehensive guide, we have explored various aspects of finding the perimeter of polygons, from basic definitions to advanced concepts. The perimeter, a fundamental geometric concept, is the total distance around a polygon. It can be calculated by summing the lengths of all the sides, a straightforward process that can be applied to both regular and irregular polygons.
For regular polygons, the formula Perimeter = number of sides × length of one side simplifies the calculation significantly. In the case of irregular polygons, each side length must be measured and added together. Understanding these calculations is crucial for solving real-world problems, such as determining the fencing required for a garden or the borders of a piece of land.
We also discussed common mistakes to avoid, such as not double-checking measurements or forgetting to use the correct units. Practice problems were provided to reinforce these concepts, allowing you to apply what you have learned in various scenarios. Visualizing the perimeter helps in grasping these ideas more effectively, as seeing the shapes and their side lengths can make the abstract more concrete.
Advanced perimeter concepts introduced methods for finding the perimeter of polygons with given vertices using the distance formula and recognizing the differences between the perimeter and the area of polygons. These skills are particularly useful in fields such as architecture, engineering, and various branches of science where precise measurements are crucial.
By mastering the calculation of the perimeter of polygons, you have gained a valuable tool for both academic and practical applications. Keep practicing with different shapes and problems to solidify your understanding and enhance your mathematical proficiency.
Cách tính chu vi của đa giác
READ MORE:
Chu vi - Tìm chu vi của bất kỳ đa giác nào