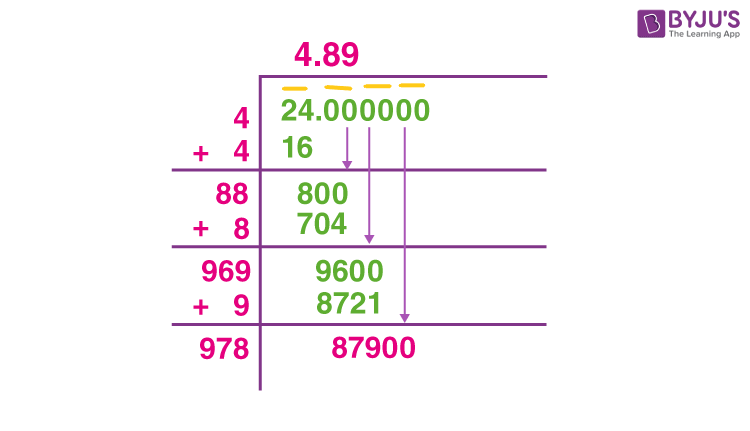
Topic square root problems: Discover how to master square root problems with ease. This comprehensive guide covers basic concepts, solving techniques, common pitfalls, and advanced applications. Whether you're a student or a math enthusiast, our step-by-step approach and practice problems will help you gain confidence and excel in solving square root problems.
Table of Content
- Square Root Problems
- Introduction to Square Root Problems
- Basic Concepts of Square Roots
- Calculating Square Roots
- Properties of Square Roots
- Solving Basic Square Root Equations
- Handling Negative Numbers and Complex Square Roots
- Common Mistakes and Pitfalls
- Advanced Square Root Problems
- Applications of Square Roots in Real Life
- Practice Problems and Solutions
- Tips and Strategies for Solving Square Root Problems
- Conclusion
- YOUTUBE: Video giải thích khái niệm về căn bậc hai một cách dễ hiểu và thú vị, giúp người xem nắm vững kiến thức cơ bản về căn bậc hai.
Square Root Problems
Square root problems often involve finding the principal square root of a number or solving equations that contain square roots. Below are various types of square root problems and methods to solve them.
Basic Square Root Calculation
The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). It is denoted as \( \sqrt{x} \).
For example:
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
Solving Square Root Equations
Equations involving square roots can be solved by isolating the square root on one side and then squaring both sides of the equation.
For example, to solve the equation:
\(\sqrt{x + 3} = 5\)
First, square both sides:
\((\sqrt{x + 3})^2 = 5^2\)
This simplifies to:
x + 3 = 25
Then, isolate \( x \) by subtracting 3 from both sides:
x = 22
Solving Quadratic Equations Using Square Roots
Quadratic equations in the form \( ax^2 + bx + c = 0 \) can sometimes be solved using the square root method, especially when the equation can be simplified to \( x^2 = d \).
For example, consider the equation:
\(x^2 = 49\)
Taking the square root of both sides gives:
\(x = \pm \sqrt{49}\)
This simplifies to:
\(x = \pm 7\)
Complex Square Roots
When dealing with negative numbers under the square root, the result is a complex number. The square root of a negative number \( -a \) is given by \( \sqrt{-a} = i\sqrt{a} \), where \( i \) is the imaginary unit.
For example:
- \(\sqrt{-4} = 2i\)
- \(\sqrt{-9} = 3i\)
Common Mistakes and Tips
- Remember that \(\sqrt{x^2} = |x|\), not \( x \).
- Always check for extraneous solutions when solving square root equations by substituting back into the original equation.
- For equations with multiple square roots, isolate and square each square root step by step.
Practice Problems
- Solve \(\sqrt{x} = 8\)
- Solve \(\sqrt{2x + 3} = 7\)
- Solve \(x^2 = 20\)
- Solve \(\sqrt{x^2 + 4x + 4} = 6\)
- Solve \(\sqrt{3x + 5} + 2 = 10\)
These examples and tips should help in understanding and solving various square root problems. Practice regularly to master these concepts!

READ MORE:
Introduction to Square Root Problems
Square root problems are fundamental in mathematics, involving the calculation and manipulation of square roots. A square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). Understanding how to solve square root problems is crucial for students and professionals in various fields.
Key concepts in square root problems include:
- Principal Square Root: The non-negative square root of a number.
- Negative Square Roots: Solutions involving negative values, particularly with complex numbers.
- Radical Sign: The symbol \( \sqrt{} \) used to denote the square root.
To solve square root problems, follow these steps:
- Identify the square root: Determine the number or expression under the radical sign.
- Isolate the square root: If the square root is part of an equation, isolate it on one side of the equation.
- Square both sides: Eliminate the square root by squaring both sides of the equation.
- Solve the resulting equation: Solve the simplified equation for the variable.
- Check for extraneous solutions: Verify that the solutions obtained are valid by substituting them back into the original equation.
Here is a simple example to illustrate:
Example: Solve \( \sqrt{x + 5} = 3 \)
- Isolate the square root: The square root is already isolated.
- Square both sides: \( (\sqrt{x + 5})^2 = 3^2 \)
- Simplify: \( x + 5 = 9 \)
- Solve for \( x \): \( x = 9 - 5 \), thus \( x = 4 \)
- Check the solution: Substitute \( x = 4 \) back into the original equation: \( \sqrt{4 + 5} = 3 \), which is true.
Mastering square root problems involves practice and familiarity with these steps. This foundation will help in tackling more complex mathematical challenges involving square roots.
Basic Concepts of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol \( \sqrt{} \). For a given number \( x \), the square root is represented as \( \sqrt{x} \).
Here are some fundamental concepts related to square roots:
- Principal Square Root: The non-negative square root of a number. For example, \( \sqrt{9} = 3 \).
- Negative Square Root: The negative counterpart of the principal square root. For instance, \( -\sqrt{9} = -3 \).
- Perfect Squares: Numbers whose square roots are integers. Examples include 1, 4, 9, 16, 25, etc.
- Non-Perfect Squares: Numbers that do not have integer square roots, resulting in irrational numbers. For example, \( \sqrt{2} \) and \( \sqrt{3} \).
- Radical Expressions: Expressions that contain a square root. For example, \( \sqrt{5} \) or \( 2\sqrt{3} \).
To calculate the square root of a number, follow these steps:
- Identify the number: Determine the number for which you want to find the square root.
- Determine if the number is a perfect square: Check if the number is a perfect square by finding an integer that, when squared, equals the original number.
- Use a calculator for non-perfect squares: For numbers that are not perfect squares, use a calculator to find an approximate value of the square root.
Examples:
- \(\sqrt{25} = 5\) (since \( 5^2 = 25 \))
- \(\sqrt{36} = 6\) (since \( 6^2 = 36 \))
- \(\sqrt{2} \approx 1.414\) (using a calculator for approximation)
Properties of square roots include:
- \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
- \(\sqrt{a^2} = |a|\)
Understanding these basic concepts of square roots is essential for solving various mathematical problems and forms the foundation for more advanced topics in algebra and calculus.
Calculating Square Roots
Calculating square roots involves finding a number that, when multiplied by itself, equals the original number. There are several methods to calculate square roots, ranging from basic estimation to using advanced algorithms.
Using Prime Factorization
For perfect squares, prime factorization can be used:
- Find the prime factors: Break down the number into its prime factors. For example, for 36, the prime factors are \(2^2 \times 3^2\).
- Pair the prime factors: Group the prime factors into pairs. For 36, we have \((2 \times 2) \) and \((3 \times 3)\).
- Take one factor from each pair: Multiply one factor from each pair to find the square root. Thus, \(\sqrt{36} = 2 \times 3 = 6\).
Using Estimation and Averaging
For non-perfect squares, estimation and averaging can provide an approximate value:
- Make an initial guess: Estimate a number close to the square root. For example, to find \(\sqrt{20}\), start with an initial guess of 4 (since \(4^2 = 16\) and \(5^2 = 25\)).
- Divide and average: Divide the original number by the guess, then average the guess and the result. For \(\sqrt{20}\), divide 20 by 4 to get 5. The average of 4 and 5 is 4.5.
- Repeat the process: Use the new average as the guess and repeat the process until the desired accuracy is reached. In this case, \(\sqrt{20} \approx 4.47\).
Using a Calculator
For quick and accurate results, a calculator is the most efficient tool:
- Enter the number and press the square root button (\(\sqrt{}\)).
- The calculator will display the square root value.
Example: To find \(\sqrt{50}\), simply enter 50 and press \(\sqrt{}\), giving approximately 7.071.
Using the Newton-Raphson Method
The Newton-Raphson method provides a more precise iterative approach:
- Initial guess: Start with an initial guess \( x_0 \).
- Iterative formula: Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \), where \( S \) is the number for which you want to find the square root.
- Repeat until convergence: Continue iterating until the difference between successive values is negligible.
Example: To find \(\sqrt{10}\) with an initial guess of 3:
- First iteration: \( x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) \approx 3.1623 \)
- Continue iterating until the desired precision is achieved.
These methods provide various ways to calculate square roots, from simple estimations to precise calculations using algorithms.
Properties of Square Roots
Understanding the properties of square roots is essential for solving square root problems efficiently. These properties help simplify expressions and solve equations involving square roots.
Basic Properties
- Non-Negative Result: The principal square root of a non-negative number is always non-negative. For example, \( \sqrt{25} = 5 \), not \(-5\).
- Square of a Square Root: The square of the square root of a number returns the original number. For instance, \( (\sqrt{7})^2 = 7 \).
- Square Root of a Square: The square root of a square of a number is the absolute value of the original number. For example, \( \sqrt{(-4)^2} = \sqrt{16} = 4 \).
Multiplication and Division Properties
- Product Property: The square root of a product is equal to the product of the square roots. Mathematically, \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \). For example, \( \sqrt{9 \times 4} = \sqrt{36} = 6 \) and \( \sqrt{9} \times \sqrt{4} = 3 \times 2 = 6 \).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots. Mathematically, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{25}{4}} = \sqrt{6.25} = 2.5 \) and \( \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} = 2.5 \).
Exponent Properties
- Square Root as an Exponent: The square root of a number can be expressed as an exponent of \( \frac{1}{2} \). For example, \( \sqrt{16} = 16^{\frac{1}{2}} = 4 \).
- Power of a Square Root: The \( n \)-th power of a square root is equal to the square root of the \( n \)-th power. Mathematically, \( (\sqrt{a})^n = a^{\frac{n}{2}} \). For instance, \( (\sqrt{5})^3 = 5^{\frac{3}{2}} \).
Rationalizing the Denominator
Rationalizing involves removing the square root from the denominator of a fraction:
- Multiply by the Conjugate: If the denominator is \( \sqrt{b} \), multiply the numerator and denominator by \( \sqrt{b} \).
- Simplify: Simplify the fraction. For example, \( \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \).
Examples and Applications
- Simplifying square root expressions: \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \).
- Solving equations: If \( x = \sqrt{y} \), then \( x^2 = y \).
- Geometry applications: Calculating the diagonal of a square with side length \( a \) using \( \sqrt{a^2 + a^2} = a\sqrt{2} \).
These properties of square roots provide a strong foundation for solving more complex mathematical problems involving square roots.

Solving Basic Square Root Equations
Solving square root equations involves isolating the square root term and then squaring both sides of the equation to eliminate the square root. Here are the steps to solve basic square root equations:
-
Isolate the Square Root: Ensure that the square root term is by itself on one side of the equation.
Example: Solve \( \sqrt{x + 3} = 5 \)
- Isolate the square root: \( \sqrt{x + 3} = 5 \)
-
Square Both Sides: Eliminate the square root by squaring both sides of the equation.
Example: \( (\sqrt{x + 3})^2 = 5^2 \)
- Results in: \( x + 3 = 25 \)
-
Solve for the Variable: Solve the resulting equation for the variable.
Example: \( x + 3 = 25 \)
- Solve: \( x = 25 - 3 \)
- Thus, \( x = 22 \)
-
Check for Extraneous Solutions: Always substitute the solution back into the original equation to check for extraneous solutions.
Example: Verify \( x = 22 \) in the original equation \( \sqrt{x + 3} = 5 \)
- Check: \( \sqrt{22 + 3} = \sqrt{25} = 5 \)
- The solution \( x = 22 \) is correct.
Here are more examples:
Example 1
Solve \( \sqrt{2x - 1} = 3 \)
- Isolate the square root: \( \sqrt{2x - 1} = 3 \)
- Square both sides: \( (\sqrt{2x - 1})^2 = 3^2 \)
- Results in: \( 2x - 1 = 9 \)
- Solve for \( x \): \( 2x = 9 + 1 \), \( 2x = 10 \), \( x = 5 \)
- Check: \( \sqrt{2(5) - 1} = \sqrt{10 - 1} = \sqrt{9} = 3 \)
- Solution: \( x = 5 \)
Example 2
Solve \( \sqrt{3x + 4} = 2 \)
- Isolate the square root: \( \sqrt{3x + 4} = 2 \)
- Square both sides: \( (\sqrt{3x + 4})^2 = 2^2 \)
- Results in: \( 3x + 4 = 4 \)
- Solve for \( x \): \( 3x = 4 - 4 \), \( 3x = 0 \), \( x = 0 \)
- Check: \( \sqrt{3(0) + 4} = \sqrt{4} = 2 \)
- Solution: \( x = 0 \)
By following these steps and practicing with additional problems, you can become proficient at solving basic square root equations.
Handling Negative Numbers and Complex Square Roots
When dealing with square roots of negative numbers, we need to introduce the concept of imaginary numbers. Imaginary numbers allow us to extend the real number system to solve equations that do not have real solutions. The fundamental imaginary unit is denoted by \(i\), where \(i\) is defined as:
\[ i = \sqrt{-1} \]
Using this definition, we can express the square root of any negative number as a multiple of \(i\). For example, consider the square root of -9:
\[ \sqrt{-9} = \sqrt{9 \cdot (-1)} = \sqrt{9} \cdot \sqrt{-1} = 3i \]
In general, the square root of a negative number \(-p\) (where \(p\) is a positive real number) can be written as:
\[ \sqrt{-p} = i\sqrt{p} \]
To better understand how to handle these numbers, let's go through a few examples and steps:
- Identify the negative number inside the square root.
- Separate the negative part by introducing \(i\).
- Simplify the remaining square root of the positive part.
Here are some additional examples:
- \(\sqrt{-16} = \sqrt{16 \cdot (-1)} = \sqrt{16} \cdot \sqrt{-1} = 4i\)
- \(\sqrt{-25} = \sqrt{25 \cdot (-1)} = \sqrt{25} \cdot \sqrt{-1} = 5i\)
Complex numbers are numbers that have both a real part and an imaginary part. A complex number is expressed in the form \(a + bi\), where \(a\) is the real part and \(b\) is the imaginary part.
For example:
- \(3 + 4i\) is a complex number where \(3\) is the real part and \(4i\) is the imaginary part.
- \(5i\) is a pure imaginary number with a real part of \(0\).
To add or subtract complex numbers, combine like terms, i.e., add the real parts together and the imaginary parts together:
\[ (3 + 2i) + (1 + 4i) = (3 + 1) + (2i + 4i) = 4 + 6i \]
Multiplication of complex numbers involves using the distributive property and the fact that \(i^2 = -1\). For example:
\[ (2 + 3i)(1 + 4i) = 2 \cdot 1 + 2 \cdot 4i + 3i \cdot 1 + 3i \cdot 4i \]
\[ = 2 + 8i + 3i + 12i^2 \]
\[ = 2 + 11i + 12(-1) \]
\[ = 2 + 11i - 12 \]
\[ = -10 + 11i \]
When dividing complex numbers, multiply the numerator and the denominator by the conjugate of the denominator to rationalize it. For instance:
\[ \frac{3 + 2i}{1 - 4i} \]
\[ = \frac{(3 + 2i)(1 + 4i)}{(1 - 4i)(1 + 4i)} \]
\[ = \frac{3 + 12i + 2i + 8i^2}{1 - 16i^2} \]
\[ = \frac{3 + 14i + 8(-1)}{1 - 16(-1)} \]
\[ = \frac{3 + 14i - 8}{1 + 16} \]
\[ = \frac{-5 + 14i}{17} \]
\[ = -\frac{5}{17} + \frac{14}{17}i \]
Understanding how to work with negative numbers and complex square roots is crucial for solving a broader range of mathematical problems, especially in higher-level mathematics and engineering applications.
Common Mistakes and Pitfalls
When solving square root problems, students often encounter several common mistakes and pitfalls. Understanding these errors can help in avoiding them and improving accuracy.
- Misinterpreting the Square Root Symbol:
One frequent error is misunderstanding the square root symbol. For example, assuming that \( \sqrt{0.9} = 0.3 \) is incorrect. The correct calculation is:
\( \sqrt{0.9} = \sqrt{\frac{9}{10}} = \frac{\sqrt{9}}{\sqrt{10}} = \frac{3}{\sqrt{10}} \). Simplifying further might require rationalizing the denominator.
- Incorrect Simplification:
Another common mistake is incorrectly simplifying expressions involving square roots. For instance:
\( 3\sqrt{3} + 3 \neq 6\sqrt{3} \). The correct simplification is:
\( 3\sqrt{3} + 3 = 3(\sqrt{3} + 1) \).
- Incorrect Addition and Subtraction:
Students often mistakenly add or subtract square roots directly, which is not generally valid:
\( \sqrt{x + y} \neq \sqrt{x} + \sqrt{y} \). For example:
\( \sqrt{9 + 16} \neq \sqrt{9} + \sqrt{16} \Rightarrow 5 \neq 3 + 4 \).
- Misapplying Square Root Properties:
Errors also occur when students misapply properties of square roots, such as:
\( \sqrt{x^2 + y^2} \neq x + y \). For example:
\( \sqrt{12^2 + 5^2} \neq 12 + 5 \Rightarrow 13 \neq 17 \).
- Incorrect Multiplication and Division:
Misunderstanding how to handle multiplication and division of square roots can lead to mistakes:
\( 3\sqrt{5} + 2\sqrt{5} \neq 6\sqrt{5} \). The correct approach is:
\( 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5} \).
- Decimal Miscalculations:
Students may miscalculate squares of decimals, for instance:
\( 0.2^2 \neq 0.4 \). The accurate calculation is:
\( 0.2^2 = 0.2 \times 0.2 = 0.04 \).
- Exponents with Variables:
When squaring terms with variables, incorrect assumptions can cause errors:
\( (4a)^2 \neq 4a^2 \). The correct result is:
\( (4a)^2 = 16a^2 \).
- Negative Numbers:
Another frequent mistake is mishandling negative numbers in squares:
\( (-3)^2 \neq -9 \). The correct calculation is:
\( (-3)^2 = 9 \).
By understanding and practicing these common errors, students can develop better mathematical habits and improve their problem-solving skills.
Advanced Square Root Problems
Advanced square root problems often involve complex expressions and require a deeper understanding of algebraic techniques. Here, we will explore several types of advanced problems, providing step-by-step solutions to enhance your skills.
1. Solving Equations with Nested Radicals
Nested radicals are expressions containing a radical within another radical. For example, consider the equation:
\[
\sqrt{2 + \sqrt{3x - 5}} = 3
\]
- First, isolate the outer square root:
\[
\sqrt{2 + \sqrt{3x - 5}} = 3 \implies 2 + \sqrt{3x - 5} = 9
\] - Simplify the equation:
\[
2 + \sqrt{3x - 5} = 9 \implies \sqrt{3x - 5} = 7
\] - Square both sides to remove the inner square root:
\[
(\sqrt{3x - 5})^2 = 7^2 \implies 3x - 5 = 49
\] - Solve for \( x \):
\[
3x - 5 = 49 \implies 3x = 54 \implies x = 18
\]
2. Solving Quadratic Equations Involving Square Roots
Quadratic equations can sometimes be solved by taking square roots. For instance:
\[
x^2 - 4x + 4 = 16
\]
- Rewrite the equation in standard form:
\[
x^2 - 4x + 4 - 16 = 0 \implies x^2 - 4x - 12 = 0
\] - Factor the quadratic expression:
\[
(x - 6)(x + 2) = 0
\] - Solve for \( x \):
\[
x - 6 = 0 \implies x = 6
\]\[
x + 2 = 0 \implies x = -2
\]
3. Solving Equations with Complex Square Roots
When dealing with negative numbers under the square root, solutions involve complex numbers. Consider the equation:
\[
x^2 + 1 = 0
\]
- Isolate \( x^2 \):
\[
x^2 = -1
\] - Take the square root of both sides, remembering to include the imaginary unit \( i \):
\[
x = \pm \sqrt{-1} = \pm i
\]
4. Solving Radical Equations with Rational Exponents
Radical expressions can also be expressed using rational exponents. For example:
\[
(2x - 3)^{\frac{3}{2}} = 27
\]
- First, isolate the term with the exponent:
\[
(2x - 3)^{\frac{3}{2}} = 27
\] - Rewrite the exponent equation:
\[
(2x - 3)^{\frac{3}{2}} = 27 \implies \left((2x - 3)^{\frac{1}{2}}\right)^3 = 27
\] - Take the cube root of both sides:
\[
(2x - 3)^{\frac{1}{2}} = 3
\] - Square both sides to solve for \( x \):
\[
2x - 3 = 9 \implies 2x = 12 \implies x = 6
\]
5. Practical Application Problem
Consider a physics problem where the displacement \( s \) is given by a formula involving a square root:
\[
s = \sqrt{2gt}
\]
If \( s = 20 \) meters and \( g = 9.8 \) m/s\(^2\), find the time \( t \).
- Substitute the known values:
\[
20 = \sqrt{2 \cdot 9.8 \cdot t}
\] - Simplify the equation:
\[
20 = \sqrt{19.6t}
\] - Square both sides:
\[
400 = 19.6t
\] - Solve for \( t \):
\[
t = \frac{400}{19.6} \approx 20.41 \text{ seconds}
\]
These examples illustrate how to tackle advanced square root problems using various algebraic techniques. Practicing these methods will help you become proficient in solving complex radical equations.

Applications of Square Roots in Real Life
Square roots are used in a wide variety of real-life applications, spanning multiple fields such as finance, engineering, science, and more. Below are some key examples demonstrating how square roots play a crucial role in everyday problems and professional scenarios.
-
Finance
In finance, square roots are used to calculate stock market volatility. Volatility is derived by taking the square root of the variance of a stock's returns, helping investors assess the risk associated with an investment.
-
Architecture
Engineers use square roots to determine the natural frequency of structures like buildings and bridges. This helps in predicting how these structures will respond to various loads, such as wind or traffic, ensuring their stability and safety.
-
Science
Square roots are prevalent in scientific calculations, such as determining the velocity of a moving object, the amount of radiation absorbed by a material, or the intensity of sound waves. These calculations are essential for developing new technologies and understanding natural phenomena.
-
Statistics
In statistics, the standard deviation, which measures the dispersion of a dataset, is the square root of the variance. This metric is crucial for data analysis and making informed decisions based on statistical data.
-
Geometry
Square roots are used in geometry to calculate distances and areas. For example, the Pythagorean theorem involves finding the length of the hypotenuse of a right triangle by taking the square root of the sum of the squares of the other two sides.
-
Computer Science
In computer programming, square roots are used in encryption algorithms, image processing, and game physics. They help in generating secure data transmissions and realistic graphics simulations.
-
Cryptography
Cryptography employs square roots in various applications, including digital signatures and secure communication channels. These mathematical principles help ensure data integrity and security.
-
Navigation
Square roots are used to compute distances between points on a map or globe. Pilots and navigators use these calculations to determine the most efficient routes and ensure accurate travel plans.
-
Electrical Engineering
Square roots are essential in electrical engineering for calculating power, voltage, and current in circuits. These calculations are critical for designing and maintaining electrical systems and devices.
-
Free-Fall Physics
When analyzing objects in free fall, the height \(h\) of an object after time \(t\) can be given by the equation \(h = h_0 - 16t^2\). Solving for time \(t\) involves taking the square root, demonstrating the use of square roots in kinematic equations.
Overall, square roots are a fundamental mathematical tool that facilitates a broad range of practical applications, making them indispensable in both academic and professional fields.
Practice Problems and Solutions
Practicing square root problems can help reinforce understanding and build confidence in solving various types of problems involving square roots. Below are some practice problems along with their solutions:
Problem 1
Find the square root of 49.
Solution:
\[
\sqrt{49} = 7
\]
Problem 2
Calculate the square root of 121.
Solution:
\[
\sqrt{121} = 11
\]
Problem 3
What is the square root of 144?
Solution:
\[
\sqrt{144} = 12
\]
Problem 4
Find the least number of 4 digits, which is a perfect square.
Solution:
The least number of 4 digits is 1024, which is \(32^2\).
Problem 5
What is the square root of 256?
Solution:
\[
\sqrt{256} = 16
\]
Problem 6
Simplify the expression: \( \sqrt{64} + \sqrt{81} \)
Solution:
\[
\sqrt{64} + \sqrt{81} = 8 + 9 = 17
\]
Problem 7
Find the square root of 1.44.
Solution:
\[
\sqrt{1.44} = 1.2
\]
Problem 8
A square has an area of 225 square units. Find the length of one side of the square.
Solution:
\[
\text{Side length} = \sqrt{225} = 15 \text{ units}
\]
Problem 9
The area of a square is 625 square meters. What is the length of one side?
Solution:
\[
\text{Side length} = \sqrt{625} = 25 \text{ meters}
\]
Problem 10
Find the smallest number that must be added to 1780 to make it a perfect square.
Solution:
The smallest number that must be added to 1780 to make it a perfect square is 69, making it 1849, which is \(43^2\).
Problem 11
There are 2401 students in a school. The P.E. teacher wants them to stand in rows and columns such that the number of rows is equal to the number of columns. Find the number of rows.
Solution:
\[
\text{Number of rows} = \sqrt{2401} = 49
\]
Problem 12
Find the cube root of 2744.
Solution:
\[
\sqrt[3]{2744} = 14
\]
Problem 13
What is the square root of 34 up to two decimal points?
Solution:
\[
\sqrt{34} \approx 5.83
\]
Problem 14
The area of a square playground is 256.6404 square meters. Find the length of one side of the playground.
Solution:
\[
\text{Side length} = \sqrt{256.6404} = 16.02 \text{ meters}
\]
Problem 15
Find the greatest number of 5 digits, which is a perfect square.
Solution:
The greatest number of 5 digits that is a perfect square is 99856, which is \(316^2\).
Problem 16
What is the square root of 29?
Solution:
\[
\sqrt{29} \approx 5.385
\]
Problem 17
Find the least number of six digits, which is a perfect square.
Solution:
The least number of six digits that is a perfect square is 100489, which is \(317^2\).
Tips and Strategies for Solving Square Root Problems
Solving square root problems can be challenging, but with the right tips and strategies, you can approach these problems with confidence. Here are some detailed steps and strategies to help you solve square root problems effectively:
- Understand the Basic Concepts:
- Remember that the square root of a number \(x\) is a number \(y\) such that \(y^2 = x\).
- Square roots can be positive or negative because both \(y\) and \(-y\) satisfy \(y^2 = x\).
- Simplify the Radicand:
- Break down the number under the square root (the radicand) into its prime factors.
- Pair the prime factors and move them outside the square root.
- For example, \(\sqrt{72} = \sqrt{2^3 \cdot 3^2} = 6\sqrt{2}\).
- Use Approximation for Non-Perfect Squares:
- Estimate the square root of non-perfect squares using nearby perfect squares.
- For instance, to approximate \(\sqrt{50}\), note that \(50\) is between \(49\) and \(64\), so \(\sqrt{50}\) is between \(7\) and \(8\).
- Apply the Square Root Property:
- Use the property that \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) to simplify expressions.
- For example, \(\sqrt{12 \cdot 3} = \sqrt{12} \cdot \sqrt{3} = 2\sqrt{3} \cdot \sqrt{3} = 2 \cdot 3 = 6\).
- Rationalize the Denominator:
- When you have a square root in the denominator, multiply the numerator and the denominator by the same square root to eliminate the square root in the denominator.
- For instance, \(\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\).
- Solve Square Root Equations:
- Isolate the square root on one side of the equation.
- Square both sides of the equation to eliminate the square root.
- Solve the resulting equation and check your solutions in the original equation.
- For example, if \(\sqrt{x+3} = 5\), then \(x+3 = 25\), so \(x = 22\).
- Use Graphical Methods:
- Plot the function and use the graph to understand the behavior of the square root function.
- This can help visualize solutions to equations involving square roots.
- Practice Regularly:
- Consistent practice helps reinforce these strategies and improves problem-solving skills.
- Work on a variety of problems to build confidence and proficiency.
By following these tips and strategies, you can develop a strong foundation for solving square root problems efficiently and accurately.
Conclusion
In conclusion, understanding and working with square roots is a fundamental skill in mathematics with applications in various fields. Mastery of square root problems can enhance problem-solving abilities and provide a strong foundation for more advanced mathematical concepts. Here are key takeaways from this guide:
- Basic Concepts: Grasping the fundamental definition and properties of square roots is essential. Remember that the square root of a number is a value that, when multiplied by itself, gives the original number.
- Calculation Techniques: We covered several methods for calculating square roots, including prime factorization, estimation, and using a calculator for more precision.
- Properties and Equations: Understanding the properties of square roots, such as the product and quotient rules, helps in simplifying complex expressions. Additionally, solving square root equations requires isolating the square root and squaring both sides of the equation.
- Handling Negatives and Complex Numbers: It's crucial to recognize that the square root of a negative number involves imaginary numbers, leading to complex solutions.
- Applications: Square roots are used in various real-life applications, from geometry and physics to finance and engineering, demonstrating their practical importance.
As you continue to practice and solve square root problems, you'll develop a deeper understanding and become more proficient. Remember, practice is key to mastering any mathematical concept. We encourage you to explore additional resources and practice problems to further enhance your skills.
By building a solid foundation in square roots, you are better prepared to tackle more advanced mathematical challenges and apply these skills in real-world scenarios. Keep exploring and learning!

Video giải thích khái niệm về căn bậc hai một cách dễ hiểu và thú vị, giúp người xem nắm vững kiến thức cơ bản về căn bậc hai.
Các Căn Bậc Hai Là Gì? | Toán Học Với Thầy J
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai một cách dễ hiểu và chi tiết, giúp người xem nắm vững kỹ năng giải quyết các vấn đề về căn bậc hai.
Cách Đơn Giản Hóa Căn Bậc Hai