Topic square root 42: The square root of 42 is a fascinating number that captures the interest of mathematicians and enthusiasts alike. In this article, we will delve into its calculation, properties, and real-life applications. Whether you are a student or just curious, join us in exploring the intriguing aspects of the square root of 42.
Table of Content
- Square Root of 42
- Introduction to Square Roots
- What is the Square Root of 42?
- How to Calculate the Square Root of 42
- Mathematical Properties of Square Roots
- Approximating the Square Root of 42
- Applications of Square Root in Real Life
- Square Root of 42 in Decimal Form
- Square Root of 42 in Radical Form
- Square Root of 42 in Exponential Form
- Graphical Representation of the Square Root of 42
- Common Mistakes in Finding the Square Root of 42
- Practice Problems Involving the Square Root of 42
- Advanced Topics Related to Square Roots
- Conclusion
- YOUTUBE: Video giới thiệu về căn bậc hai của 42, giải thích cách tính và các ứng dụng thực tế của nó trong cuộc sống.
Square Root of 42
The square root of 42 is approximately represented as:
\( \sqrt{42} \approx 6.480740698 \)
Here are some details about the square root of 42:
- Exact value: \( \sqrt{42} \)
- Approximate decimal value: \( 6.480740698 \)
- It is an irrational number.
- The square of \( \sqrt{42} \) is approximately 42.
| Calculation method | Approximate value |
| Using a calculator | \( 6.480740698 \) |
| Using numerical methods | \( 6.480740698 \) |

READ MORE:
Introduction to Square Roots
Square roots are mathematical operations that find the original number which, when multiplied by itself, results in a given number. The square root is denoted by the radical symbol \( \sqrt{} \). For example, the square root of 42 is written as \( \sqrt{42} \).
Understanding square roots is fundamental in mathematics, as they appear in various branches such as algebra, geometry, and calculus. Here is a step-by-step approach to grasp the concept of square roots:
- Definition: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). For example, \( \sqrt{42} \approx 6.48 \) because \( 6.48^2 \approx 42 \).
- Symbol: The square root is represented by the radical symbol \( \sqrt{} \). Thus, the square root of 42 is expressed as \( \sqrt{42} \).
- Properties of Square Roots:
- \( \sqrt{x} \times \sqrt{x} = x \)
- \( \sqrt{x \times y} = \sqrt{x} \times \sqrt{y} \)
- \( \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} \) for \( y \neq 0 \)
- \( \sqrt{x^2} = |x| \)
- Examples:
- \( \sqrt{4} = 2 \) because \( 2^2 = 4 \)
- \( \sqrt{9} = 3 \) because \( 3^2 = 9 \)
- \( \sqrt{16} = 4 \) because \( 4^2 = 16 \)
- Calculation Methods:
- Prime Factorization: Breaking down the number into its prime factors and pairing them.
- Long Division Method: A manual method similar to long division used for more accurate results.
- Using a Calculator: The most straightforward way to find the square root, especially for non-perfect squares like 42.
In conclusion, square roots are a crucial part of mathematics, providing a foundation for understanding more complex mathematical concepts. The square root of 42, while not a perfect square, is approximately 6.48, illustrating the beauty and complexity of irrational numbers.
What is the Square Root of 42?
The square root of 42 is a number which, when multiplied by itself, equals 42. This can be expressed as:
\[
\sqrt{42}
\]
Since 42 is not a perfect square, its square root is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form is non-repeating and non-terminating. To understand the square root of 42, let's explore its approximate value and the methods used to find it.
- Approximate Value:
Using a calculator, we find that:
\[
\sqrt{42} \approx 6.48074069840786
\]For practical purposes, this value is often rounded to two decimal places:
\[
\sqrt{42} \approx 6.48
\] - Prime Factorization Method:
- Break down 42 into its prime factors: \(42 = 2 \times 3 \times 7\).
- The square root of 42 is not simplified further using prime factorization, as it does not form perfect pairs of prime factors.
- Long Division Method:
- This method involves a step-by-step manual process similar to long division to find a more accurate value of the square root.
- It is often used for educational purposes to understand the mechanics behind finding square roots.
- Using a Calculator:
- The most efficient method to find the square root of 42 is using a scientific calculator.
- Simply enter 42 and press the square root button to obtain the value \( \approx 6.48 \).
In conclusion, the square root of 42 is approximately 6.48, a value that can be obtained using various methods such as calculators or long division. This value is significant in various mathematical contexts and applications, providing insight into the properties of irrational numbers.
How to Calculate the Square Root of 42
Calculating the square root of 42 involves several methods, each with its own level of precision and complexity. Here, we'll explore three primary methods: using a calculator, the long division method, and the approximation method.
- Using a Calculator:
- The simplest and most accurate method to find the square root of 42 is by using a scientific calculator.
- Steps:
- Turn on the calculator.
- Enter the number 42.
- Press the square root (\( \sqrt{} \)) button.
- Read the result, which will be approximately 6.48074069840786.
- Long Division Method:
This manual method provides a step-by-step approach to approximate the square root. Here’s how you can do it:
- Step-by-Step:
- Write the number 42 as 42.000000 to facilitate the long division process.
- Pair the digits starting from the decimal point: (42)(00)(00)(00).
- Find the largest number whose square is less than or equal to the first pair (42). This number is 6 because \(6^2 = 36\).
- Subtract 36 from 42 to get 6. Bring down the next pair of zeros to get 600.
- Double the current quotient (6) to get 12. Find a digit (X) such that 12X * X is less than or equal to 600. The digit is 4 because 124 * 4 = 496.
- Subtract 496 from 600 to get 104. Bring down the next pair of zeros to get 10400.
- Repeat the process until you achieve the desired precision.
- Step-by-Step:
- Approximation Method:
- This method is useful for quick, rough estimates without a calculator.
- Steps:
- Identify two perfect squares between which 42 lies. These are 36 (\(6^2\)) and 49 (\(7^2\)).
- Since 42 is closer to 36 than 49, we start with an initial guess of 6.5.
- Square 6.5 to get 42.25, which is close to 42.
- Refine the guess using the formula: \[ \text{New guess} = \frac{\text{Old guess} + \frac{42}{\text{Old guess}}}{2} \] For example, with an old guess of 6.5: \[ \text{New guess} = \frac{6.5 + \frac{42}{6.5}}{2} \approx 6.480769 \]
- Repeat the process until the guess stabilizes around 6.48.
Each method has its own applications, whether you need a quick estimate or a precise calculation. Using a calculator is the fastest way, while the long division method and approximation method provide deeper insights into the calculation process.
Mathematical Properties of Square Roots
Square roots have several important mathematical properties that are fundamental in various branches of mathematics. Understanding these properties helps in simplifying complex mathematical expressions and solving equations efficiently. Here are some key properties:
- Product Property:
The square root of a product is equal to the product of the square roots of the factors. For any non-negative numbers \(a\) and \(b\):
\[
\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}
\]Example:
\[
\sqrt{42 \cdot 2} = \sqrt{84} \approx 9.17
\]\[
\sqrt{42} \cdot \sqrt{2} \approx 6.48 \cdot 1.41 = 9.14
\] - Quotient Property:
The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. For any non-negative numbers \(a\) and \(b\) (with \(b \neq 0\)):
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]Example:
\[
\sqrt{\frac{42}{2}} = \sqrt{21} \approx 4.58
\]\[
\frac{\sqrt{42}}{\sqrt{2}} \approx \frac{6.48}{1.41} \approx 4.59
\] - Power Property:
The square root of a number raised to the power of 2 is the absolute value of the number:
\[
\sqrt{a^2} = |a|
\]Example:
\[
\sqrt{42^2} = \sqrt{1764} = 42
\] - Sum and Difference Property:
The square root of a sum or difference of two squares can be simplified in special cases, though not generally:
For any non-negative numbers \(a\) and \(b\):
\[
\sqrt{a^2 + b^2} \quad \text{and} \quad \sqrt{a^2 - b^2}
\]However, these expressions often do not simplify nicely without additional context.
- Nested Radicals Property:
Nesting radicals involves expressing a square root within another square root:
\[
\sqrt{\sqrt{a}} = a^{\frac{1}{4}}
\]Example:
\[
\sqrt{\sqrt{42}} \approx \sqrt{6.48} \approx 2.55
\]
Understanding these properties enables us to manipulate and simplify expressions involving square roots, making it easier to solve mathematical problems. They play a crucial role in algebra, calculus, and other advanced areas of mathematics.
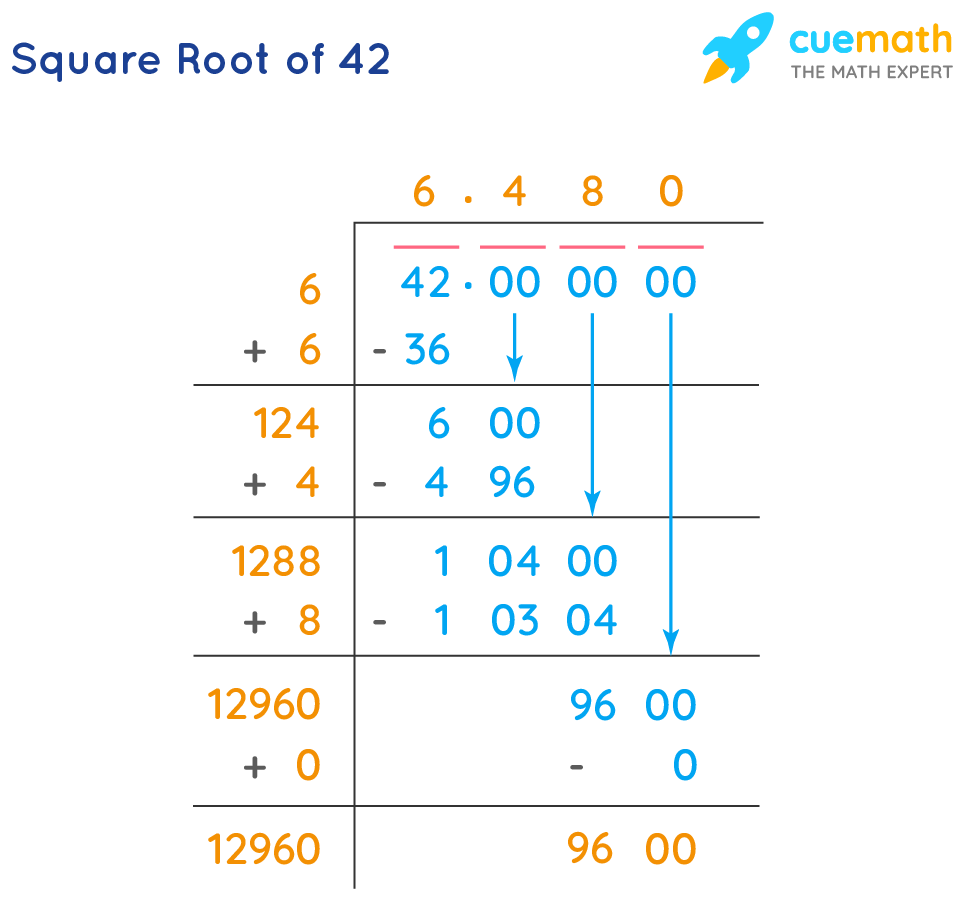
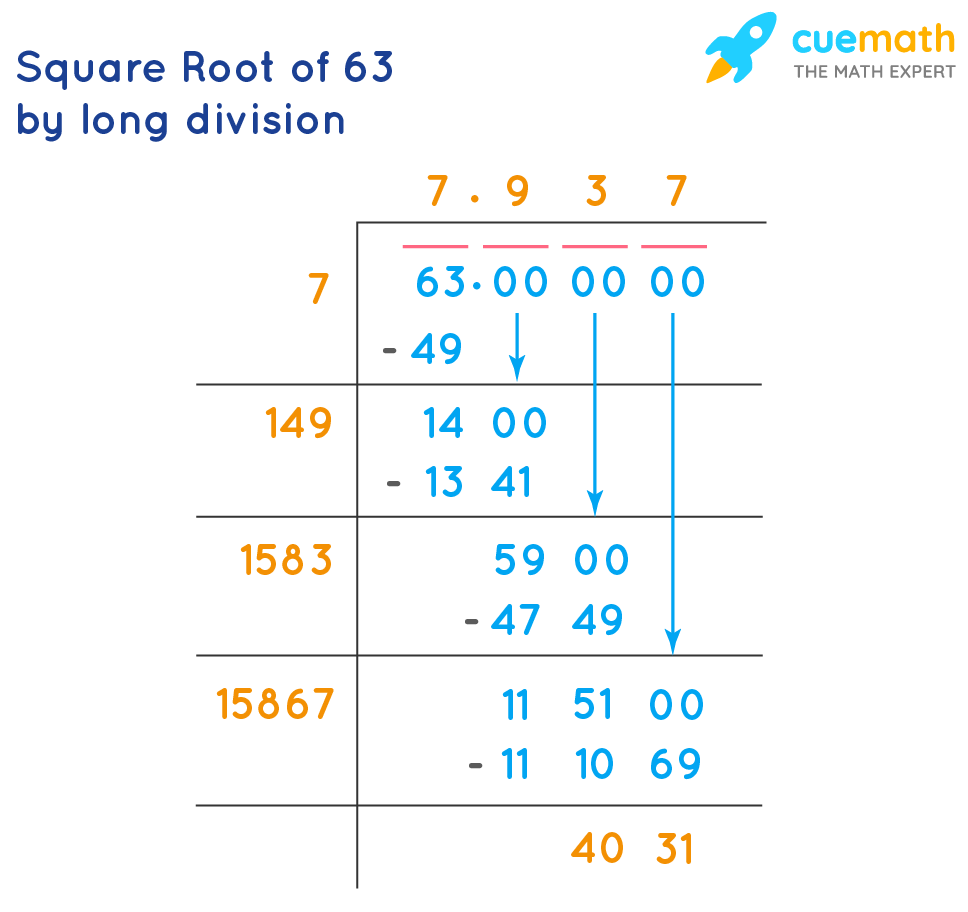
Approximating the Square Root of 42
Approximating the square root of 42 can be done using several methods, each providing a different level of precision. Here are the most common techniques used to approximate \( \sqrt{42} \):
- Using a Calculator:
- The simplest and most accurate way to approximate \( \sqrt{42} \) is to use a scientific calculator.
- Steps:
- Turn on the calculator.
- Enter the number 42.
- Press the square root (\( \sqrt{} \)) button.
- Read the result: \( \sqrt{42} \approx 6.48074069840786 \).
- Prime Factorization Method:
Although 42 is not a perfect square, breaking it down into its prime factors can help in understanding its roots:
- Factorize 42: \( 42 = 2 \times 3 \times 7 \).
- Since 42 is not a perfect square, we recognize that \( \sqrt{42} \) is an irrational number.
- This method shows the components of 42 but does not directly help in numerical approximation.
- Long Division Method:
This manual process provides a step-by-step approximation:
- Write 42 as 42.000000 to facilitate the long division process.
- Pair the digits starting from the decimal point: (42)(00)(00)(00).
- Find the largest number whose square is less than or equal to the first pair (42). This number is 6 because \(6^2 = 36\).
- Subtract 36 from 42 to get 6. Bring down the next pair of zeros to get 600.
- Double the current quotient (6) to get 12. Find a digit (X) such that 12X * X is less than or equal to 600. The digit is 4 because 124 * 4 = 496.
- Subtract 496 from 600 to get 104. Bring down the next pair of zeros to get 10400.
- Repeat the process until the desired precision is achieved.
- Approximation Method:
- This method involves using nearby perfect squares to estimate \( \sqrt{42} \).
- Steps:
- Identify two perfect squares between which 42 lies. These are 36 (\(6^2\)) and 49 (\(7^2\)).
- Since 42 is closer to 36 than 49, start with an initial guess of 6.5.
- Square 6.5 to get 42.25, which is close to 42.
- Refine the guess using the formula: \[ \text{New guess} = \frac{\text{Old guess} + \frac{42}{\text{Old guess}}}{2} \] For example, with an old guess of 6.5: \[ \text{New guess} = \frac{6.5 + \frac{42}{6.5}}{2} \approx 6.480769 \]
- Repeat the process until the guess stabilizes around 6.48.
Each method offers a different approach to approximating \( \sqrt{42} \). Using a calculator is the most straightforward and accurate, while manual methods provide deeper insights into the process and are useful for educational purposes.
Applications of Square Root in Real Life
The concept of square roots extends beyond pure mathematics and finds applications in various real-life scenarios. Here are some practical uses of square roots in different fields:
- Engineering and Physics:
- Structural Analysis: Engineers use square roots to determine the stress and strain on materials, ensuring buildings and bridges can withstand loads.
- Wave Equations: In physics, the square root function is essential in wave equations, describing how waves propagate through different media.
- Finance:
- Standard Deviation: Square roots are used in calculating standard deviation, a measure of the amount of variation or dispersion in a set of values.
- Compound Interest: Financial analysts use square roots to calculate the compound interest and growth rates over time.
- Medicine:
- Dosage Calculations: Medical professionals use square roots to determine the correct dosages of medications based on body surface area.
- Medical Imaging: In imaging techniques like MRI, square roots help in processing and interpreting the images.
- Computer Science:
- Algorithm Design: Square roots are used in various algorithms, including those for cryptography and data compression.
- Graphics and Simulations: Square roots help in rendering realistic graphics and simulations, particularly in calculating distances and lighting effects.
- Astronomy:
- Distance Calculations: Astronomers use square roots to calculate distances between celestial bodies, using the inverse square law of light.
- Orbital Mechanics: Square roots are essential in determining the orbits of planets and satellites.
- Everyday Life:
- Area Calculations: Square roots help in finding the dimensions of squares and rectangles, especially in home improvement projects.
- Cooking: Recipes sometimes require scaling, and square roots are useful in adjusting ingredient quantities proportionally.
The square root function is a powerful mathematical tool with a wide range of applications across different disciplines. Its ability to simplify complex calculations and provide accurate results makes it invaluable in both professional and everyday contexts.
Square Root of 42 in Decimal Form
The square root of 42 is an irrational number, meaning it cannot be expressed exactly as a simple fraction. Its decimal form is non-repeating and non-terminating. The approximate value of the square root of 42 up to several decimal places is:
\(\sqrt{42} \approx 6.48074069840786\)
For practical purposes, it is often rounded to a more manageable number of decimal places. Here are a few common approximations:
- Rounded to 2 decimal places: \( \sqrt{42} \approx 6.48 \)
- Rounded to 3 decimal places: \( \sqrt{42} \approx 6.481 \)
- Rounded to 4 decimal places: \( \sqrt{42} \approx 6.4807 \)
To understand the decimal form of the square root of 42 more deeply, let’s explore the steps to calculate it:
- Initial Estimate: Start with an initial estimate close to the square root of 42. Since \( \sqrt{36} = 6 \) and \( \sqrt{49} = 7 \), the square root of 42 is between 6 and 7.
- Refinement: Use a method such as the Newton-Raphson method to refine this estimate. The Newton-Raphson iteration formula for square roots is:
- \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{42}{x_n} \right) \)
Start with \( x_0 = 6.5 \) (a value between 6 and 7) and iterate:
- \( x_1 = \frac{1}{2} \left( 6.5 + \frac{42}{6.5} \right) \approx 6.47826087 \)
- \( x_2 = \frac{1}{2} \left( 6.47826087 + \frac{42}{6.47826087} \right) \approx 6.48074070 \)
- Convergence: Continue the iteration until the value converges to a stable number. The more iterations, the closer the approximation.
Using a calculator or a computational tool will give the value directly. However, understanding the process helps in comprehending the nature of square roots and their decimal representations.
Thus, the square root of 42 in decimal form is approximately \(6.48074069840786\), and for most practical applications, it can be rounded as needed to the desired precision.
Square Root of 42 in Radical Form
The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 42, its square root can be expressed in radical form.
To represent the square root of 42 in radical form, we look at its prime factorization. The prime factors of 42 are 2, 3, and 7. This means we can write 42 as:
\(42 = 2 \times 3 \times 7\)
Using this, we can express the square root of 42 in radical form as:
\[
\sqrt{42} = \sqrt{2 \times 3 \times 7}
\]
Since these factors are prime and cannot be simplified further, the simplest radical form of the square root of 42 is:
\[
\sqrt{42}
\]
To elaborate on the properties of this radical:
- It is already in its simplest form.
- It cannot be simplified into a product of smaller square roots.
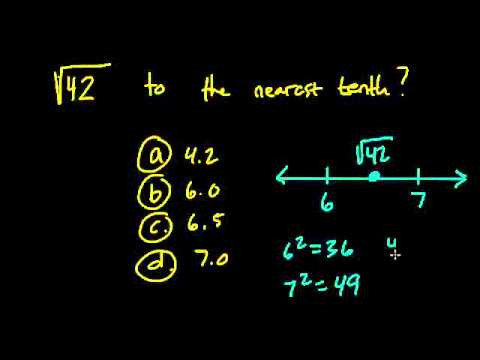
Square Root of 42 in Exponential Form
To understand the square root of 42 in exponential form, it's important to first grasp the concept of exponents and radicals.
In mathematics, the square root of a number can be expressed using an exponent. Specifically, the square root of a number \( n \) is written as \( n^{\frac{1}{2}} \). This is because taking the square root is the same as raising the number to the power of 1/2.
Thus, the square root of 42 in exponential form is:
\[
\sqrt{42} = 42^{\frac{1}{2}}
\]
Here's a step-by-step explanation:
- Identify the number you want to find the square root of. In this case, it is 42.
- Express the square root using the exponent 1/2. This follows from the property of exponents and radicals where the square root of \( n \) is \( n^{\frac{1}{2}} \).
- Write it in exponential form: \( 42^{\frac{1}{2}} \).
In summary, the square root of 42 can be conveniently written in exponential form as \( 42^{\frac{1}{2}} \), which is a useful representation in various mathematical contexts, such as calculus and algebra.
To see how this fits into different forms, consider:
- Radical Form: \( \sqrt{42} \)
- Exponential Form: \( 42^{\frac{1}{2}} \)
This exponential notation is particularly useful when applying certain mathematical operations and transformations, making it a versatile tool in both theoretical and applied mathematics.
Graphical Representation of the Square Root of 42
Graphically representing the square root of 42 helps in visualizing its value and understanding its placement on the number line. Here's how you can do it:
1. **Number Line Representation:**
- Draw a horizontal line and mark it with evenly spaced intervals. Label these intervals with integers, such as 0, 1, 2, 3, and so on.
- The square root of 42, approximately 6.48, falls between the integers 6 and 7. Mark this position on the number line.
Here is a simple representation:
\[
\begin{array}{ccccccc}
0 & 1 & 2 & 3 & 4 & 5 & 6 & \sqrt{42} & 7 & 8 \\
\end{array}
\]
2. **Graph of \( y = \sqrt{x} \):**
The function \( y = \sqrt{x} \) can be graphed to show the relationship between \( x \) and its square root. To plot the point where \( x = 42 \):
- On the x-axis, locate the value 42.
- On the y-axis, locate the approximate value 6.48, since \( \sqrt{42} \approx 6.48 \).
- Plot the point (42, 6.48) on the graph.
Below is a rough sketch of this graph:
\[
\begin{array}{c|c}
x & y = \sqrt{x} \\
\hline
0 & 0 \\
1 & 1 \\
4 & 2 \\
9 & 3 \\
16 & 4 \\
25 & 5 \\
36 & 6 \\
42 & \approx 6.48 \\
49 & 7 \\
\end{array}
\]
The curve of \( y = \sqrt{x} \) increases gradually, and the point (42, 6.48) lies on this curve, showing the square root of 42.
3. **Graphical Tools and Calculators:**
Using graphing calculators or software like Desmos can provide an accurate and detailed graph of the function \( y = \sqrt{x} \). These tools allow you to zoom in and see the exact placement of the square root of 42.
4. **Understanding Through Geometry:**
If we consider a right-angled triangle with legs of lengths \( a \) and \( b \), and the hypotenuse as \( c \), using the Pythagorean theorem \( a^2 + b^2 = c^2 \), setting \( c = \sqrt{42} \) provides a geometric interpretation. For example:
If \( a = 6 \) and \( b \approx 2.48 \), then:
\[
6^2 + 2.48^2 = 36 + 6.1504 \approx 42
\]
This geometric representation helps in visualizing \( \sqrt{42} \) as the hypotenuse of a right-angled triangle.
These graphical methods provide a comprehensive understanding of the square root of 42 and its applications in various mathematical contexts.
Common Mistakes in Finding the Square Root of 42
Finding the square root of 42 can sometimes lead to common mistakes. Understanding these mistakes helps in avoiding them and ensuring accurate calculations. Here are some of the typical errors:
- Incorrect Approximation:
One common mistake is inaccurately approximating the square root of 42. The square root of 42 is approximately 6.48, but it is often rounded improperly. Ensure that the approximation is done correctly, using more decimal places for greater accuracy when necessary.
- Misunderstanding Radicals and Exponents:
Another mistake is confusing the representation of the square root in radical and exponential forms. Remember that:
\[
\sqrt{42} = 42^{\frac{1}{2}}
\]Using the incorrect form or misunderstanding these representations can lead to errors.
- Arithmetic Errors:
Basic arithmetic mistakes can occur when calculating the square root manually or using a calculator. Double-check each step to ensure calculations are correct.
- Incorrect Use of the Calculator:
When using a calculator, input errors are common. Make sure to use the square root function properly. For example, entering the number and then pressing the square root button, or using the correct sequence if the calculator requires it:
\[
\text{Input: } 42 \rightarrow \sqrt{x} \text{ button}
\] - Confusing Square Roots with Other Roots:
Sometimes, there is confusion between the square root and other roots (such as cube roots). The notation for square root is distinct and should not be mixed up:
\[
\sqrt{42} \neq \sqrt[3]{42}
\] - Assuming Rational Results:
Expecting a simple rational number can be a mistake. The square root of 42 is an irrational number, meaning it cannot be expressed as a simple fraction. Accepting the irrational nature of the result is crucial:
\[
\sqrt{42} \approx 6.48074069840786 \ldots
\]
To avoid these common mistakes, it's important to practice and verify calculations, understand the mathematical concepts, and use reliable tools. Properly approaching the problem ensures accurate and reliable results.
Practice Problems Involving the Square Root of 42
To enhance your understanding of the square root of 42, here are several practice problems. These problems will help reinforce the concepts and methods involved in working with square roots.
-
Exact and Approximate Values
- Find the exact value of \( \sqrt{42} \) in simplest radical form.
- Calculate the approximate value of \( \sqrt{42} \) to two decimal places.
-
Square Root Equations
- Solve for \( x \) in the equation \( x^2 = 42 \).
- Solve for \( x \) in the equation \( 2x^2 - 3 = 81 \).
-
Simplifying Square Roots
- Simplify \( \sqrt{42 \times 6} \).
- Simplify \( \frac{\sqrt{42}}{2} \).
-
Applications
- A square has an area of 42 square units. Find the length of one side of the square.
- If a right triangle has one leg measuring \( \sqrt{42} \) units and the other leg measuring 6 units, find the length of the hypotenuse.
-
Complex Problems
- Find the value of \( x \) if \( 2\sqrt{x} = \sqrt{42} \).
- Simplify \( \sqrt{42} + \sqrt{18} \) and express the answer in simplest radical form.
These problems range from basic calculations to more complex applications, helping you to deepen your understanding of the square root of 42 and its uses in different mathematical contexts.
Advanced Topics Related to Square Roots
Square roots are a fundamental concept in mathematics, but there are advanced topics that extend beyond basic calculations. Below, we explore several advanced topics related to square roots, with a focus on deeper mathematical concepts and applications.
1. Irrational Numbers and Their Properties
The square root of 42, like many square roots, is an irrational number. This means it cannot be expressed as a simple fraction. Irrational numbers have several unique properties:
- Non-repeating, non-terminating decimal expansions
- Cannot be exactly represented as a ratio of two integers
- They are part of the real numbers but not the rational numbers
2. Simplifying Radical Expressions
While the square root of 42 cannot be simplified to a smaller radical, understanding the process of simplifying radicals is important. For example, simplifying involves breaking it down to .
3. Conjugates and Rationalizing the Denominator
In more advanced algebra, we often encounter expressions that require rationalizing the denominator. This involves multiplying by the conjugate. For example, to rationalize , multiply by to get .
4. Complex Numbers and Square Roots
Square roots are also fundamental in the study of complex numbers. The square root of a negative number involves imaginary numbers. For instance, the square root of -42 is represented as , where is the imaginary unit.
5. Quadratic Equations and the Square Root Method
The square root method is a technique used to solve quadratic equations of the form . For example, solving gives .
6. Numerical Methods for Approximating Square Roots
Various numerical methods can approximate square roots, such as:
- Newton's Method: Iterative method to find successively better approximations to the roots of a real-valued function.
- Bisection Method: A root-finding method that repeatedly divides an interval in half and selects the subinterval in which a root must lie.
7. Square Roots in Higher Dimensions
In linear algebra, the concept of square roots extends to matrices. A matrix has a square root if there exists a matrix such that . This topic explores eigenvalues, eigenvectors, and diagonalization.
8. Continued Fractions and Square Roots
Square roots of non-square integers can be represented as continued fractions. These fractions are periodic and provide insights into the nature of these roots. For example, the continued fraction representation of reveals its repetitive structure.
Understanding these advanced topics provides a deeper insight into the significance and applications of square roots in various fields of mathematics and science.
Conclusion
The exploration of the square root of 42 reveals a rich tapestry of mathematical concepts and practical applications. Understanding how to calculate and approximate square roots enhances our comprehension of numerical relationships and their relevance in various fields.
Key takeaways include:
- Definition: The square root of 42 is a number which, when multiplied by itself, equals 42.
- Calculation Methods: Several methods can be used to find the square root of 42, including the long division method, estimation, and the use of a calculator.
- Approximation: The square root of 42 is approximately 6.4807. This value is derived through iterative methods or calculator-based computations.
- Mathematical Properties: Square roots have unique properties such as being non-negative and involving rational and irrational numbers depending on the radicand.
- Forms: The square root of 42 can be expressed in different forms: decimal form (6.4807), radical form (\(\sqrt{42}\)), and exponential form (421/2).
- Graphical Representation: Graphing the function \(y = \sqrt{x}\) provides a visual understanding of how the square root of 42 fits within the larger context of square roots.
- Applications: Square roots are used in numerous real-life applications, including engineering, physics, statistics, and even art.
- Common Mistakes: Avoiding errors such as incorrect approximations and misunderstandings about the properties of square roots is crucial for accurate calculations.
In summary, the square root of 42, like other square roots, is more than just a number; it represents a fundamental concept that bridges various areas of mathematics and practical applications. By understanding and correctly applying these principles, we can solve complex problems and appreciate the elegance of mathematical relationships.
Video giới thiệu về căn bậc hai của 42, giải thích cách tính và các ứng dụng thực tế của nó trong cuộc sống.
Hiểu về Căn Bậc Hai của 42
READ MORE:
Video giới thiệu về căn bậc hai của 42, giải thích cách tính và các ứng dụng thực tế của nó trong cuộc sống hàng ngày.
Căn Bậc Hai của 42