Topic square root math definition: The square root of a number is a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. This concept is pivotal in various mathematical applications, including solving quadratic equations and simplifying expressions. Explore the basics, properties, and practical examples of square roots to enhance your mathematical understanding and problem-solving skills.
Table of Content
- Square Root Math Definition
- Introduction
- Definition of Square Root
- How to Calculate Square Roots
- Methods for Finding Square Roots
- Prime Factorization Method
- Long Division Method
- Approximating Square Roots
- Square Roots of Non-Perfect Squares
- Applications of Square Roots
- Square Roots in Real Life
- Square Roots and Quadratic Equations
- Common Mistakes and Misconceptions
- Summary
- Additional Resources
- YOUTUBE:
Square Root Math Definition
The square root of a number is a value that, when multiplied by itself, gives the original number. It is represented using the radical symbol "√". For example, the square root of 9 is 3 because \( 3 \times 3 = 9 \).
Definition
The square root of any number \( x \) is a number \( y \) such that \( y^2 = x \). In mathematical terms, this can be expressed as:
\[ y = \sqrt{x} \]
Properties of Square Roots
- If a number is a perfect square, it has an integer square root.
- The square root of a product is the product of the square roots: \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\).
- The square root of a quotient is the quotient of the square roots: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- Negative numbers do not have real square roots because a square is never negative.
Calculating Square Roots
There are several methods to calculate square roots, including:
- Prime Factorization
- Repeated Subtraction Method
- Long Division Method
- Estimation Method
Perfect Squares
Perfect squares are numbers that are squares of integers. Here is a list of perfect squares up to 15:
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
Examples
Let's consider some examples to illustrate the concept:
- The square root of 25 is 5 because \( 5 \times 5 = 25 \).
- The square root of 36 is 6 because \( 6 \times 6 = 36 \).
Square Roots of Decimal Numbers
The square root of decimal numbers can also be calculated. For example, the square root of 2.25 is 1.5 because \( 1.5 \times 1.5 = 2.25 \).
Square Roots of Negative Numbers
For negative numbers, the square root is not defined in the set of real numbers. However, in the set of complex numbers, the square root of a negative number is an imaginary number. For example, \( \sqrt{-1} = i \) where \( i \) is the imaginary unit.

READ MORE:
Introduction
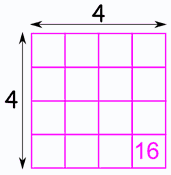
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because 4 x 4 = 16. The square root is denoted by the radical symbol (√). There are both positive and negative square roots for any given number, as both 3 x 3 and -3 x -3 equal 9, making the square roots of 9 both 3 and -3.
Perfect squares, such as 1, 4, 9, 16, and 25, have whole numbers as their square roots. Non-perfect squares, however, result in irrational numbers. For example, the square root of 2 is approximately 1.41421. Estimating square roots of non-perfect squares involves methods like the prime factorization or long division method.
Understanding square roots is fundamental in solving quadratic equations and simplifying radical expressions. This knowledge extends to recognizing patterns in numbers and applying various algorithms, such as the Bhaskara-Brouncker and Newton's iteration methods, to find approximate values for square roots.
Square roots are essential in various mathematical contexts, including geometry, algebra, and calculus. They are also used in practical applications such as physics, engineering, and computer science.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, yields the original number. For instance, the square root of 9 is 3, because \(3 \times 3 = 9\). This can be expressed as \( \sqrt{9} = 3 \). The concept of square roots is fundamental in mathematics, particularly in algebra and geometry.
Mathematically, if \( y \) is the square root of \( a \), it can be represented as \( y = \sqrt{a} \) or \( y^2 = a \). Here are some key points:
- The square root symbol is \( \sqrt{} \), also known as the radical symbol.
- The number under the radical symbol is called the radicand.
Examples:
- \( \sqrt{4} = 2 \), because \( 2 \times 2 = 4 \).
- \( \sqrt{9} = 3 \), because \( 3 \times 3 = 9 \).
- \( \sqrt{16} = 4 \), because \( 4 \times 4 = 16 \).
For non-perfect squares, the square root is not an integer but a decimal or a fraction. For example, \( \sqrt{2} \approx 1.414 \).
Square roots can also be negative. For example, the square roots of 25 are \( 5 \) and \( -5 \), because both \( 5 \times 5 = 25 \) and \( (-5) \times (-5) = 25 \).
Understanding square roots is crucial for solving quadratic equations, simplifying radicals, and performing various calculations in mathematics.
How to Calculate Square Roots
Calculating square roots can be approached using several methods. Here's a detailed step-by-step guide to some of the most common techniques:
- Prime Factorization Method
- Find the prime factors of the number.
- Pair the prime factors.
- Take one factor from each pair and multiply them together.
- If there are any factors that do not pair, place them inside the square root symbol.
- Prime factors: 2 × 2 × 3 × 3 × 7 × 7
- Pairs: (2 × 2), (3 × 3), (7 × 7)
- Square root: 2 × 3 × 7 = 42
- Therefore, √1764 = 42
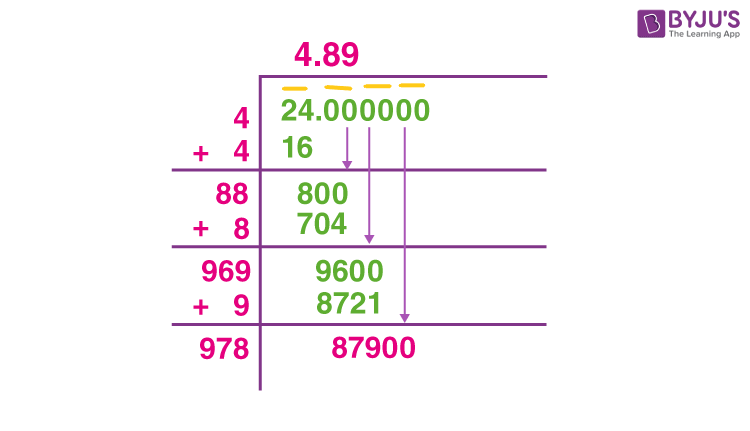
For example, to find the square root of 1764:
- Long Division Method
- Place a bar over every pair of digits, starting from the right.
- Divide the leftmost number by the largest number whose square is less than or equal to it.
- Bring down the next pair of digits and repeat the process.
- Place bars: 5|29
- Divide: 2 (since 2² = 4 ≤ 5)
- Bring down next pair: 43
- Multiply and subtract: 43 × 3 = 129 (remainder is 0)
- Therefore, √529 = 23
For example, to find the square root of 529:
- Approximation Method
- Identify two consecutive perfect squares between which the number lies.
- Estimate the square root as a value between these perfect squares.
- Use iterative methods to refine the approximation.
- Between 1² and 2² (1 and 4)
- Initial guess: 1.5
- Refinement: 1.4 (since 1.4² = 1.96 is closer to 2 than 1.5² = 2.25)
- Therefore, √2 ≈ 1.414
For example, to estimate √2:
Each method has its own applications and advantages, making it useful for different types of problems involving square roots.
Methods for Finding Square Roots
There are several methods to find the square root of a number:
- Prime Factorization Method: Decompose the number into prime factors and extract pairs of identical factors.
- Estimation Method: Approximate the square root using known perfect squares around the number.
- Long Division Method: Apply a long division-like process to systematically find the square root.
- Babylonian Method (or Heron's Method): Use an iterative algorithm that converges to the square root.
- Newton's Method: Apply calculus to iteratively refine an initial guess to the square root.
Prime Factorization Method
The prime factorization method for finding the square root involves the following steps:
- Step 1: Determine the prime factors of the number whose square root you want to find.
- Step 2: Pair up identical factors from the prime factorization.
- Step 3: Take one factor from each pair.
- Step 4: Multiply these selected factors together to get the square root of the original number.
Long Division Method
The long division method for finding the square root involves the following steps:
- Step 1: Group the digits of the number into pairs, starting from the decimal point and working left.
- Step 2: Find the largest number whose square is less than or equal to the leftmost pair of digits.
- Step 3: Divide the number formed by the leftmost pair of digits by this number. This gives the first digit of the square root.
- Step 4: Bring down the next pair of digits to the right of the remainder.
- Step 5: Double the current quotient and guess the next digit of the square root.
- Step 6: Repeat steps 3 to 5 until all pairs of digits have been used.
Approximating Square Roots
Approximating square roots can be achieved through various methods:
- Estimation: Use known perfect squares around the number to estimate its square root.
- Linear Approximation: Use the first-order Taylor series expansion around a known point to approximate the square root.
- Babylonian Method: Iteratively refine a guess by averaging it with the original number divided by the current guess.
- Newton's Method: Iteratively refine an initial guess using the function and its derivative.
Square Roots of Non-Perfect Squares
Finding the square root of non-perfect squares involves the following steps:
- Estimation: Use approximation methods such as the Babylonian method or Newton's method to find a close estimate.
- Decimal Approximation: Express the square root as a decimal using long division or a calculator for more precision.
- Continued Fractions: Represent the square root as a continued fraction to obtain a rational approximation.
- Exact Form: Leave the square root in radical form if exactness is required, without simplifying further.

Applications of Square Roots
Square roots find applications in various fields:
- Geometry: Calculating side lengths in geometric shapes such as squares, rectangles, and right triangles.
- Physics: Determining magnitudes of vectors, calculating distances, and solving problems involving velocity and acceleration.
- Engineering: Estimating forces, stresses, and designing structures based on calculations involving square roots.
- Finance: Analyzing interest rates, risk assessments, and calculating returns on investments using formulas that involve square roots.
- Statistics: Computing standard deviations, error margins, and variability in data sets.
Square Roots in Real Life
Square roots have practical applications in everyday situations:
- Measurement: Calculating the length of sides in squares, rectangles, and other shapes.
- Engineering: Determining the size and dimensions of structural elements in buildings and bridges.
- Finance: Assessing risk and volatility in financial markets through calculations involving square roots.
- Technology: Used in algorithms for image processing, signal processing, and cryptography.
- Natural Sciences: Calculating magnitudes in physics, such as electric field strengths and wave amplitudes.
Square Roots and Quadratic Equations
Square roots are closely related to quadratic equations:
- Quadratic Formula: The solutions to a quadratic equation \( ax^2 + bx + c = 0 \) can be found using the formula \( x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}} \), where \( \sqrt{{b^2 - 4ac}} \) involves the square root.
- Discriminant: The expression \( b^2 - 4ac \) under the square root in the quadratic formula determines the nature of the solutions:
- If \( b^2 - 4ac > 0 \), the equation has two distinct real roots.
- If \( b^2 - 4ac = 0 \), the equation has exactly one real root (a repeated root).
- If \( b^2 - 4ac < 0 \), the equation has two complex conjugate roots.
- Geometric Interpretation: The roots of a quadratic equation correspond to the x-intercepts of the parabola represented by the equation.
Common Mistakes and Misconceptions
There are several common mistakes and misconceptions related to square roots:
- Misconception: Thinking that the square root of a negative number is always undefined in real numbers.
- Mistake: Incorrectly simplifying square roots without considering the domain restrictions.
- Misconception: Believing that square roots of different numbers always result in integers or rational numbers.
- Mistake: Using incorrect methods to approximate or calculate square roots, leading to inaccurate results.
- Misconception: Assuming that square roots are only applicable to perfect squares.
- Mistake: Misinterpreting the role of square roots in quadratic equations, particularly the discriminant.

Summary
The concept of square roots is fundamental in mathematics, offering a way to understand the relationship between numbers and their roots. This summary highlights the key points discussed in this document.
- Introduction: Square roots are essential in various fields of mathematics and practical applications, providing insights into the relationships and properties of numbers.
- Definition of Square Root: A square root of a number is a value that, when multiplied by itself, gives the original number. The square root of \(x\) is denoted as \(\sqrt{x}\).
- Properties of Square Roots: Square roots have several properties, such as \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) and \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- How to Calculate Square Roots: Methods include prime factorization, long division, and approximation techniques.
- Methods for Finding Square Roots: Various methods are used to find square roots, each with its own steps and accuracy levels.
- Prime Factorization Method: This method involves breaking down a number into its prime factors and pairing them to find the square root.
- Long Division Method: A traditional method that provides a systematic way to find square roots by dividing and averaging.
- Approximating Square Roots: Techniques such as using a calculator or iterative methods like Newton's method help in approximating square roots.
- Square Roots of Non-Perfect Squares: Non-perfect squares have irrational square roots, which can be approximated but not expressed exactly as fractions.
- Applications of Square Roots: Square roots are used in various fields including geometry, physics, engineering, and statistics.
- Square Roots in Real Life: Practical examples include calculating areas, understanding scientific data, and solving quadratic equations.
- Square Roots and Quadratic Equations: Solving quadratic equations often involves finding the square roots of the discriminant.
- Common Mistakes and Misconceptions: Misunderstandings such as confusing square roots with square numbers, and errors in calculation, are addressed.
- Additional Resources: Further reading and tools for a deeper understanding of square roots.
In conclusion, understanding square roots involves recognizing their definitions, properties, and applications. The methods for calculating and approximating square roots are varied, each serving different needs. The practical applications highlight the importance of square roots in both academic and real-world contexts.
Additional Resources
Here are some additional resources for further exploration and understanding of square roots:
- - A comprehensive article covering the definition, properties, and historical background of square roots, including their applications in various mathematical contexts.
- - Detailed explanations on how to find square roots using different methods, properties of square roots, and solved examples.
- - An easy-to-understand guide that covers the basics of square roots, including examples and practice problems to reinforce learning.
- - Provides a deeper dive into the concept of square roots, including advanced topics and practice problems for those looking to challenge themselves.
- - A detailed resource on the mathematical properties and algorithms for calculating square roots, including historical methods and advanced concepts.
- - A useful reference for understanding the basic and advanced aspects of square roots, with examples and practical applications.
Định Nghĩa Căn Bậc Hai Toán Học | Video của Thầy J
READ MORE:
CĂN BẬC HAI 🚀 Căn Bậc Hai Là Gì? 👨🏻🚀 Toán Học Cho Trẻ Em