Topic square root curve calculator: Discover the power of the Square Root Curve Calculator, a versatile tool for plotting and analyzing the square root function. Whether you're a student, teacher, or professional, this calculator simplifies the visualization process, making it easier to understand and interpret mathematical concepts. Start exploring the fascinating world of square root curves today!
Table of Content
- Square Root Curve Calculator
- Introduction
- Understanding Square Root Functions
- Features of a Square Root Curve Calculator
- Plotting the Square Root Curve
- Interactive Graphing Tools
- Steps to Use the Calculator
- Customizing the Graph
- Analyzing the Square Root Function
- Mathematical Properties of the Square Root Curve
- Applications of Square Root Curves
- Examples and Use Cases
- Common Issues and Troubleshooting
- Additional Resources and References
- YOUTUBE: Video hướng dẫn cách vẽ đồ thị hàm căn bậc hai bằng cách sử dụng biến đổi để thu hút người xem và sửa chính tả.
Square Root Curve Calculator
A square root curve calculator helps in generating and plotting the curve of the square root function, which is represented mathematically as \( f(x) = \sqrt{x} \). This tool allows users to visualize the function and understand its properties, including its domain and range.
Features
- Function Plotting: Generates the graph of \( f(x) = \sqrt{x} \).
- Interactive Graph: Allows users to adjust the range of x-values to see how the curve changes.
- Coordinate Points: Displays key points on the curve, such as \( (0, 0) \) and \( (1, 1) \).
- Derivative and Tangent Lines: Optionally shows the derivative of the function and tangent lines at specific points.
Usage Instructions
- Enter the range of x-values you want to explore (e.g., from 0 to 10).
- Click the "Plot" button to generate the curve.
- Use the interactive features to zoom in or out and observe different sections of the curve.
- For a detailed analysis, view the tangent lines and derivative.
Mathematical Background
The square root function is defined as:
The domain of the square root function is \( x \geq 0 \), and the range is \( y \geq 0 \). The function increases at a decreasing rate as \( x \) increases.
Example Calculation
To calculate the square root of 4:
Visualization
The graph below illustrates the typical shape of the square root curve:
Applications
- Physics: Used in equations involving time and speed.
- Engineering: Helps in calculations related to waveforms and signals.
- Finance: Applied in models for growth rates and returns.
READ MORE:
Introduction
The Square Root Curve Calculator is an advanced tool designed to help users plot and analyze the square root function, \( f(x) = \sqrt{x} \). This function, which appears frequently in various mathematical and scientific contexts, produces a curve that starts at the origin and gradually rises, becoming less steep as x increases. Understanding this curve is essential for interpreting growth patterns, waveforms, and other phenomena in fields such as physics, engineering, and finance.
With the Square Root Curve Calculator, users can:
- Visualize the square root curve: Generate accurate graphs of the function over specified ranges.
- Explore function behavior: Adjust x-values and observe how the curve changes, enhancing comprehension of the function’s characteristics.
- Analyze key points: Identify important points on the curve, such as intercepts and regions where the function changes most rapidly.
- Access interactive features: Utilize tools for zooming and panning to examine different parts of the curve in detail.
This calculator is particularly useful for:
- Students seeking to grasp fundamental concepts in algebra and calculus.
- Teachers demonstrating the properties of square root functions in the classroom.
- Professionals applying mathematical models to real-world problems.
By simplifying the process of plotting and analyzing the square root function, the Square Root Curve Calculator makes it easier to engage with complex mathematical ideas and applications.
Understanding Square Root Functions
The square root function is a fundamental concept in mathematics, commonly represented as \( y = \sqrt{x} \). This function is characterized by its ability to map a given input \( x \) to its square root, producing the output \( y \). The graph of this function, known as the square root curve, exhibits unique properties that make it applicable in various fields, including geometry, physics, and finance.
Properties of the Square Root Function
- Domain: The domain of the square root function is \( x \geq 0 \), as the square root of a negative number is not defined in the set of real numbers.
- Range: The range of the square root function is \( y \geq 0 \), since the output of the square root function is always non-negative.
- Behavior: The function starts at the origin (0,0) and increases gradually, showing a decreasing rate of growth as \( x \) increases.
Graphical Representation
The square root curve is a visual representation of the square root function. It is characterized by a gentle upward slope that becomes less steep as the value of \( x \) increases. Each point on the curve represents a pair \((x, \sqrt{x})\).
Mathematical Notation and Calculation
The square root function can be expressed as:
\[ y = \sqrt{x} \]
Where:
- \( y \) is the output or the square root of \( x \)
- \( x \) is the input value
For example, if \( x = 9 \), then \( y = \sqrt{9} = 3 \).
Applications of the Square Root Function
The square root function is utilized in various disciplines:
- Geometry: It is used to determine the length of the hypotenuse in right-angled triangles, according to the Pythagorean theorem.
- Physics: The function helps in analyzing projectile motion and calculating time of flight, where the trajectory can be described using square root relationships.
- Finance: Financial analysts use the square root function to model risk and return relationships, as risk often increases at a non-linear rate relative to returns.
Visualizing the Square Root Curve
Using a square root curve calculator, one can easily plot and analyze the function. These calculators typically allow users to input values and visualize the resulting curve, facilitating a deeper understanding of the mathematical relationships.
Here is an example of how a square root curve might be plotted:
| x | \( \sqrt{x} \) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
This table highlights how the square root function translates input values \( x \) into their corresponding square roots \( \sqrt{x} \).
In conclusion, understanding the square root function and its graphical representation is crucial for various applications in mathematics and science. The square root curve calculator serves as an excellent tool for visualizing and analyzing these functions, providing valuable insights into their properties and applications.
Features of a Square Root Curve Calculator
A robust square root curve calculator offers a plethora of features to enhance user experience and facilitate mathematical exploration. Some key features include:
- Input Flexibility: Users can input single or multiple values for computation. This flexibility allows for both simple and complex calculations, accommodating a variety of user needs.
- Real-Time Visualization: The calculator provides instantaneous plotting of square root curve charts. This feature helps users to understand the relationship between input values and their square roots by visualizing the curve dynamically as values are entered.
- Customization Options: Users can adjust parameters to tweak the appearance and style of the curve. This includes changing colors, scales, and other graphical elements to tailor the visualization to specific preferences or presentation requirements.
- Export Functionality: The ability to export charts and data for further analysis or documentation purposes. This feature is particularly useful for students, educators, and professionals who need to include graphs in reports or presentations.
- Interactive Interface: A user-friendly design with intuitive controls for seamless navigation. The interactive interface ensures that users of all skill levels can efficiently utilize the calculator without a steep learning curve.
Overall, these features make the square root curve calculator a valuable tool for anyone looking to explore or demonstrate the properties of square root functions. Whether for educational purposes, data analysis, or professional presentations, the calculator provides comprehensive functionality to meet diverse needs.
Plotting the Square Root Curve
Plotting the square root curve involves understanding the function \( f(x) = \sqrt{x} \) and how it behaves on a graph. This section provides a step-by-step guide to plot the square root curve accurately using interactive graphing tools.
-
Understanding the Function:
The square root function is defined as \( f(x) = \sqrt{x} \), where \( x \geq 0 \). This means that the function is only defined for non-negative values of \( x \).
-
Setting Up the Axes:
- Label the x-axis as "Input (x)" and the y-axis as "Output (f(x))".
- Ensure the x-axis starts at 0 since the square root function is not defined for negative values.
-
Plotting Key Points:
- Start with key points such as (0,0), (1,1), (4,2), and (9,3).
- For each \( x \) value, calculate \( f(x) \) and plot the point \((x, f(x))\) on the graph.
x f(x) = √x 0 0 1 1 4 2 9 3 -
Drawing the Curve:
After plotting the key points, draw a smooth curve through these points to represent the function \( f(x) = \sqrt{x} \). The curve should start at the origin (0,0) and increase gradually, flattening out as \( x \) becomes larger.
-
Using Graphing Tools:
Interactive graphing tools can help visualize the square root curve more effectively:
- Enter the function \( f(x) = \sqrt{x} \) into the graphing tool.
- Adjust the viewing window to focus on the positive x-axis.
- Use zoom and pan features to explore different sections of the curve.
Interactive Graphing Tools
Interactive graphing tools are essential for visualizing and understanding the behavior of the square root function \( f(x) = \sqrt{x} \). These tools provide dynamic and user-friendly interfaces that allow for real-time manipulation of the graph. Here’s a detailed guide on how to use these tools effectively:
-
Selecting a Graphing Tool:
- Choose an online graphing calculator such as Desmos, GeoGebra, or Wolfram Alpha.
- Ensure the tool supports function plotting and offers interactive features like zooming and panning.
-
Entering the Function:
- Open the graphing tool and locate the input field for functions.
- Type in the square root function \( f(x) = \sqrt{x} \) or use the tool's function library to select the square root function.
-
Customizing the Graph:
- Adjust the viewing window to focus on the positive x-axis and y-axis since \( x \geq 0 \).
- Set appropriate ranges for x and y axes, for example, \( x \) from 0 to 10 and \( y \) from 0 to 3.5.
- Use the tool’s settings to modify the appearance of the graph, such as line color and thickness.
-
Exploring the Graph:
- Utilize zoom in and zoom out features to examine different parts of the curve in detail.
- Pan across the graph to move the viewable area without changing the zoom level.
- Hover over or click on points along the curve to see their exact coordinates.
-
Adding Annotations and Points:
- Mark key points on the graph such as \((0,0)\), \((1,1)\), \((4,2)\), and \((9,3)\).
- Add labels or notes to these points to highlight their significance.
-
Saving and Sharing the Graph:
- Save the graph as an image or export it in a suitable format offered by the tool.
- Share the graph via a link or embed it in a webpage or document for further analysis and discussion.
Steps to Use the Calculator
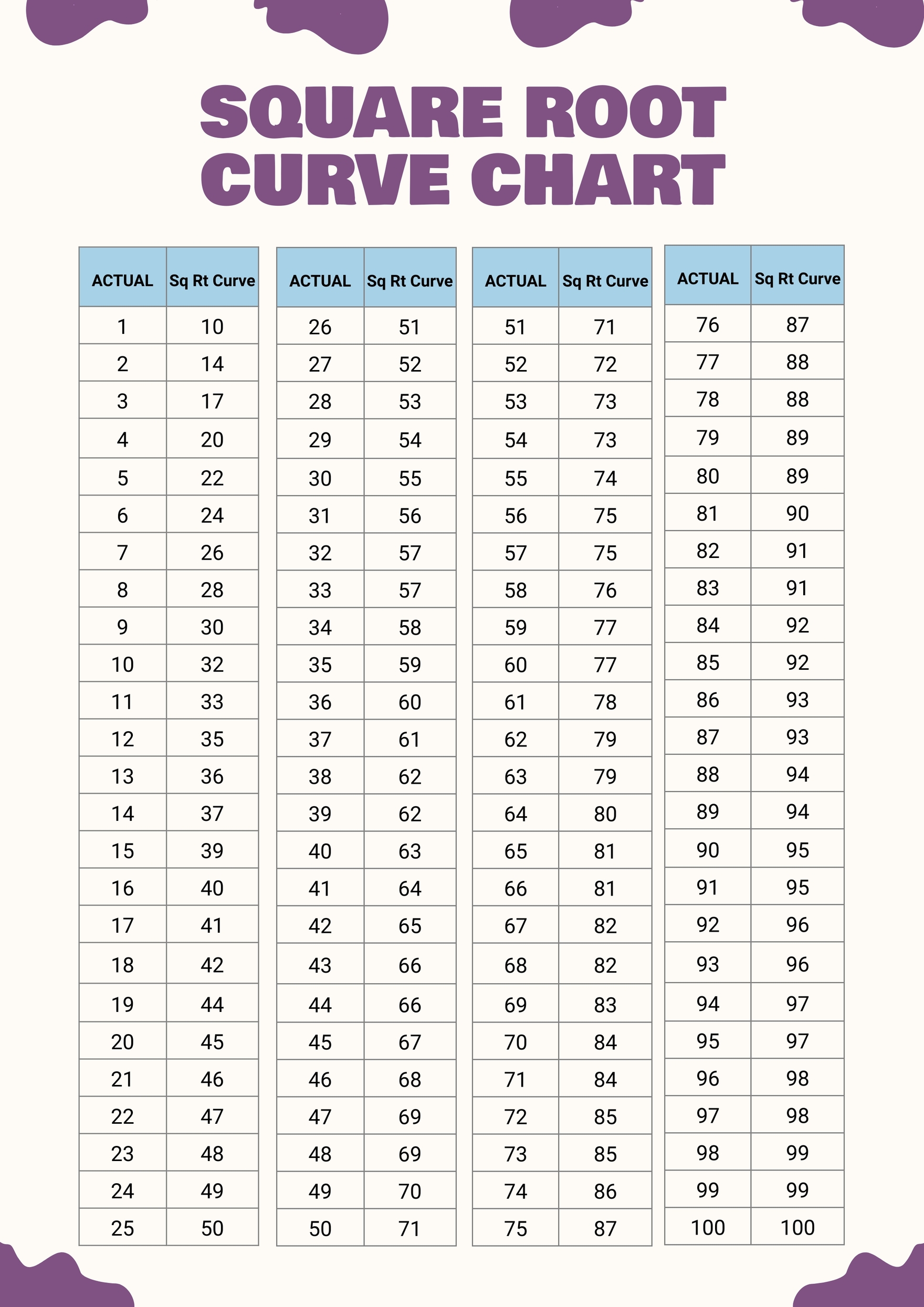
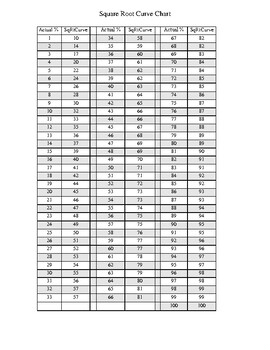
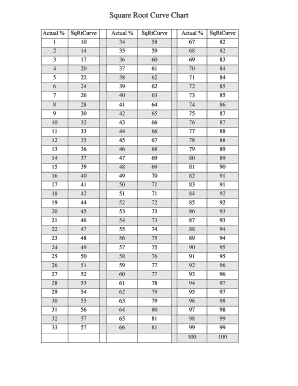
Using a Square Root Curve Calculator is straightforward. Here are the detailed steps to help you make the most of this tool:
-
Access the Calculator: Open the Square Root Curve Calculator on your preferred website.
-
Input the Percentage Grade: Enter the student's percentage grade into the input field provided. This value should be a decimal between 0 and 1 if using a normalized system, or a percentage value directly if the calculator allows for it.
-
Calculate the Square Root Curve Grade: Click the "Calculate" button to compute the square root curve grade. The calculator uses the formula:
\[ SRG = \sqrt{G} \times 10 \]
Where:
- \( SRG \) = Square Root Curve Grade
- \( G \) = Student's percentage grade
-
Review the Result: The calculator will display the square root curve grade. This result can be used to understand the adjusted grade after applying the square root curve.
-
Analyze the Outcome: Compare the original percentage grade with the square root curve grade to see how the adjustment has impacted the student's performance.
-
Utilize the Result: Use the adjusted grade for further academic assessments or grading purposes as needed.
By following these steps, you can easily use the Square Root Curve Calculator to adjust and analyze student grades efficiently.
Customizing the Graph
Customizing the graph in a square root curve calculator allows you to tailor the visual representation to better suit your analysis and presentation needs. Here are the detailed steps to customize the graph effectively:
-
Adjusting the Range of Input Values:
- Enter the desired range of input values in the provided fields. This helps in focusing on specific sections of the square root curve.
- For example, if you want to analyze the curve between 0 and 100, set the minimum value to 0 and the maximum value to 100.
-
Changing the Graph Scale:
- Select the appropriate scale for the x and y axes to ensure the graph is neither too compressed nor too stretched.
- You can choose between linear and logarithmic scales depending on the nature of your data and the details you wish to emphasize.
-
Customizing the Appearance:
- Modify the color, thickness, and style of the curve line to enhance clarity and visual appeal. This can be done using the graph settings menu.
- Common options include solid, dashed, or dotted lines, and a variety of color palettes to distinguish different data sets or curves.
-
Adding Labels and Annotations:
- Include labels for the x and y axes to clearly indicate what each axis represents. For example, label the x-axis as "Input Values" and the y-axis as "Square Root".
- Add annotations to highlight key points on the graph, such as the origin or significant intersections, which can provide additional context or emphasis.
-
Exporting the Customized Graph:
- Once satisfied with the customization, use the export feature to save the graph as an image file (PNG, JPEG, etc.) for use in reports or presentations.
- Ensure the resolution is appropriate for the intended use to maintain clarity and quality.
By following these steps, you can create a customized and informative graph that effectively communicates the properties and applications of the square root function.
Analyzing the Square Root Function
The square root function, denoted as \( f(x) = \sqrt{x} \), is a fundamental mathematical function with unique properties and diverse applications. Analyzing this function helps in understanding its behavior, characteristics, and the insights it provides in various fields.
Properties of the Square Root Function
- Domain and Range: The domain of the square root function is \( x \geq 0 \), as the square root of a negative number is not defined in the set of real numbers. The range of the function is also \( y \geq 0 \), because the square root of any non-negative number is non-negative.
- Graph: The graph of \( y = \sqrt{x} \) is a curve that starts at the origin (0,0) and increases gradually. The curve is concave down, meaning it gets flatter as \( x \) increases.
- Continuity and Differentiability: The square root function is continuous and differentiable for all \( x \geq 0 \). The derivative of \( \sqrt{x} \) is \( \frac{1}{2\sqrt{x}} \), indicating that the slope of the tangent to the curve decreases as \( x \) increases.
- Behavior at Specific Points: At \( x = 0 \), the function value is \( y = 0 \). As \( x \) approaches infinity, \( y \) also approaches infinity but at a decreasing rate.
Steps to Analyze the Function
- Identify the Domain: Determine the values of \( x \) for which the function is defined. For \( \sqrt{x} \), the domain is \( x \geq 0 \).
- Plot Key Points: Plot points like (0,0), (1,1), (4,2), and (9,3) to understand the shape of the graph. These points help visualize how the function behaves at specific values.
- Examine the End Behavior: Analyze how the function behaves as \( x \) approaches its boundaries. For \( \sqrt{x} \), as \( x \) approaches infinity, \( \sqrt{x} \) increases indefinitely.
- Calculate the Derivative: Find the derivative to understand the rate of change of the function. The derivative \( \frac{d}{dx} \sqrt{x} = \frac{1}{2\sqrt{x}} \) indicates the slope of the tangent at any point \( x \).
- Interpret Real-World Applications: Apply the understanding of the square root function in various contexts such as physics (e.g., projectile motion), finance (e.g., risk assessment), and geometry (e.g., distances in coordinate systems).
Applications of the Square Root Function
- Geometry: Used in calculating distances between points in a plane using the distance formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
- Physics: Appears in formulas involving acceleration and gravitational forces, such as in determining the time of flight of a projectile.
- Finance: Used in models that assess risk and return, where the relationship between risk and potential reward can be represented using a square root function.
Understanding and analyzing the square root function provides a deeper insight into mathematical concepts and their practical applications. This fundamental function is integral to various fields, making its study both important and fascinating.
Mathematical Properties of the Square Root Curve
The square root curve is a graphical representation of the square root function, \( f(x) = \sqrt{x} \). This function has several important mathematical properties that make it unique and useful in various applications.
Domain and Range
- Domain: The domain of the square root function is all non-negative real numbers, \( x \geq 0 \), since the square root of a negative number is not defined in the set of real numbers.
- Range: The range of the square root function is also all non-negative real numbers, \( y \geq 0 \), as the output of the square root function is never negative.
Intercepts
The square root curve has a single intercept:
- Y-intercept: The curve intersects the y-axis at \( (0,0) \).
- X-intercept: The curve intersects the x-axis at \( (0,0) \).
Behavior and Shape
- The square root function is monotonically increasing, meaning it continuously rises as \( x \) increases.
- The curve is concave down, as the rate of increase decreases with increasing \( x \).
Symmetry
The square root function is not symmetric. It does not exhibit symmetry with respect to either the y-axis or the origin.
Asymptotes
The square root curve does not have any asymptotes. As \( x \) approaches infinity, \( \sqrt{x} \) also approaches infinity, but it does so without approaching a fixed line.
Continuity and Differentiability
- The square root function is continuous for all \( x \geq 0 \).
- The function is differentiable for all \( x > 0 \). The derivative of the square root function is \( f'(x) = \frac{1}{2\sqrt{x}} \), which shows how the slope of the curve changes.
Graphical Representation
The graph of the square root function can be represented as:

Transformation
Transformations of the square root function include translations, reflections, and dilations:
- Vertical Translation: \( f(x) = \sqrt{x} + k \)
- Horizontal Translation: \( f(x) = \sqrt{x - h} \)
- Vertical Stretch/Compression: \( f(x) = a\sqrt{x} \)
- Reflection: Reflecting across the x-axis: \( f(x) = -\sqrt{x} \)
These transformations can shift, stretch, compress, or flip the graph of the square root function, allowing for a wide range of applications in different contexts.
Applications
- Geometry: Used in calculating distances, areas, and other geometric properties.
- Physics: Appears in formulas involving motion, such as the relationship between velocity, time, and distance.
- Economics: Used in modeling diminishing returns and other economic behaviors.
Applications of Square Root Curves
Square root curves are fundamental in various fields of science, engineering, and everyday life. Their unique properties make them useful in diverse applications, which include:
- Physics and Engineering: Square root functions describe the relationship between quantities in various physical laws. For example:
- In kinematics, the displacement of an object under uniform acceleration relates to the square root of time.
- In electrical engineering, the root mean square (RMS) value of an alternating current (AC) signal is derived using square root calculations.
- The intensity of sound and light waves often diminishes with the square root of the distance from the source.
- Economics: Square root functions model certain economic behaviors and relationships:
- The utility theory uses square root functions to represent the diminishing marginal utility of wealth.
- Production functions sometimes incorporate square root terms to reflect diminishing returns to scale.
- Biology: Growth patterns in biology can be represented using square root functions:
- The metabolic rate of organisms often scales with the square root of their mass.
- The diffusion of substances across cell membranes follows a square root relationship with respect to time.
- Statistics: Square root transformations stabilize variance and normalize distributions:
- In data analysis, transforming data using the square root can make skewed distributions more symmetric.
- Variance stabilizing transformations, such as the Anscombe transformation, utilize square root functions.
- Computer Graphics: Rendering algorithms and graphical representations use square root functions:
- Square root calculations are essential for distance computations in 2D and 3D graphics.
- Lighting models in graphics often use square root functions to simulate realistic shading effects.
The versatility of square root functions and their curves make them invaluable tools across these and many other domains, providing insights and solutions to complex problems.
Examples and Use Cases
Square root curves are not just mathematical abstractions; they have practical applications across various fields. Below are some examples and use cases that illustrate the utility of square root functions.
1. Geometry and Physics
Square root functions often appear in geometry and physics. Here are a couple of scenarios:
- Pythagorean Theorem: In a right-angled triangle, the length of the hypotenuse is determined using the square root of the sum of the squares of the other two sides. This is mathematically represented as \( c = \sqrt{a^2 + b^2} \), where \( a \) and \( b \) are the lengths of the legs of the triangle, and \( c \) is the hypotenuse.
- Projectile Motion: The time of flight or range of a projectile can be calculated using square root functions, helping to predict its trajectory accurately.
2. Finance
In finance, square root curves are used to model various phenomena:
- Risk Assessment: The relationship between risk and return is often non-linear. Square root functions help model how increasing risk affects potential returns, which is critical for making informed investment decisions.
- Compound Interest: When calculating compound interest, especially for fractional compounding periods, square root functions can simplify the computations and provide insights into interest accrual over time.
3. Engineering
Engineers utilize square root curves in several ways:
- Fluid Dynamics: The velocity of fluid flow in certain scenarios can be expressed as a square root function of pressure difference, aiding in the design and analysis of fluid systems.
- Signal Processing: In analyzing signals, especially when dealing with noise and distortions, the square root function helps in normalizing and interpreting data accurately.
4. Education and Grading Systems
Square root functions are sometimes used to adjust scores in educational settings:
- Grade Curving: A common use of the square root function is to curve student grades upward, making the distribution of grades more equitable. For example, if a raw score \( G \) is curved using the formula \( \text{Curved Grade} = \sqrt{G} \times 10 \), a raw score of 64 becomes 80 when curved.
5. Health and Medicine
In the health sector, square root functions find applications in various analyses:
- Drug Dosage Calculations: The effective dosage of certain medications may be determined using square root functions, especially when dealing with dosages that vary with body surface area or weight.
- Growth Patterns: Modeling biological growth patterns often involves square root functions to describe how growth rates change over time.
6. Software and Game Development
Square root functions are essential in programming and game development:
- Graphics and Animation: In computer graphics, square root functions help in calculating distances and rendering curves smoothly, providing more realistic animations.
- Physics Engines: Many physics engines use square root functions to simulate real-world phenomena like gravity and collision impacts, enhancing the realism of virtual environments.
Interactive Example
Use the interactive square root curve calculator below to visualize how different values of \( x \) produce corresponding \( y \) values on the square root curve:
Calculator Interface:
Example Calculations
| Input (x) | Output (√x) |
|---|---|
| 4 | 2 |
| 16 | 4 |
| 25 | 5 |
| 49 | 7 |
As shown in the table, the square root curve provides a straightforward way to find the square roots of perfect squares. For non-perfect squares, the calculator can quickly compute and plot these values, offering a clear visual understanding of the relationship between the variables.
Common Issues and Troubleshooting
Using a square root curve calculator can be straightforward, but users may encounter various issues. Below is a list of common problems and their solutions to ensure a smooth experience.
1. Incorrect Input Format
One of the most common issues is entering inputs in the wrong format. Square root functions typically expect non-negative numbers. If you enter negative values or non-numeric characters, the calculator may produce errors or unexpected results.
- Issue: Inputting negative values or non-numeric characters.
- Solution: Ensure that the input is a non-negative number. The square root function is only defined for non-negative real numbers. For negative numbers, consider using complex numbers if supported, where \( \sqrt{-x} = i\sqrt{x} \).
2. Out of Range Errors
Some calculators have specific input ranges. Inputting numbers outside this range can cause errors.
- Issue: Input values are too large or too small.
- Solution: Check the documentation of the calculator to understand the valid input range. Adjust your inputs to fall within these limits to avoid out-of-range errors.
3. Calculation Precision
Square root calculations can sometimes produce results with many decimal places, leading to precision errors in certain applications.
- Issue: Results have too many decimal places, leading to precision issues.
- Solution: Use the rounding feature if available, or manually round the results to the desired number of decimal places. This is especially useful in fields like finance or engineering where precision is crucial.
4. Graph Plotting Issues
When visualizing the square root curve, users might face issues with the graph display, such as a non-visible curve or incorrect scaling.
- Issue: The graph is not displaying correctly or the curve is not visible.
- Solution: Verify that the plotting range is appropriate for the input values. Adjust the x and y-axis limits to ensure that the square root curve is visible. For instance, if you're plotting \( y = \sqrt{x} \), ensure that the x-axis starts from zero or a positive value.
5. Incorrect Interpretation of Results
Misunderstanding how to interpret the results of square root calculations can lead to incorrect conclusions.
- Issue: Misinterpreting the square root values in practical applications.
- Solution: Remember that the square root function \( \sqrt{x} \) returns the principal (non-negative) square root. For applications requiring both positive and negative roots, consider both \( \sqrt{x} \) and \( -\sqrt{x} \).
6. Performance Issues with Large Inputs
Calculators may struggle with very large inputs, resulting in slow performance or crashes.
- Issue: Slow performance or application crash with large inputs.
- Solution: Break down the problem into smaller parts if possible, or use specialized software designed to handle large numbers efficiently. For instance, you can use a logarithmic transformation to simplify calculations involving very large numbers: \( \log(\sqrt{x}) = \frac{1}{2} \log(x) \).
7. Browser Compatibility
Some online calculators may not work well on all browsers or devices.
- Issue: The calculator does not display or function correctly on certain browsers or devices.
- Solution: Try accessing the calculator on a different browser or device. Ensure your browser is up to date. For best results, use modern browsers like Chrome, Firefox, or Safari.
8. Software Bugs
Occasionally, the calculator itself may have bugs or glitches that affect its functionality.
- Issue: Unexpected behavior or errors due to software bugs.
- Solution: Check if there are any updates available for the calculator software. Report the issue to the developer or support team. As a temporary fix, try using a different calculator or method to verify the results.
Additional Tips
To avoid these common issues, here are some general tips:
- Always double-check your inputs for accuracy.
- Understand the limitations and capabilities of your calculator.
- Familiarize yourself with the basic properties of square root functions to better interpret the results.
Additional Resources and References
To further your understanding of square root curves and their applications, the following resources offer comprehensive insights, interactive tools, and educational materials. These references will help you explore the mathematical principles behind square root functions, their graphical representations, and practical uses in various fields.
Online Calculators and Graphing Tools
- Desmos Graphing Calculator: An interactive tool that allows you to graph square root functions and explore their properties. Visit to create and analyze your own square root curves.
- Calculator.net Square Root Calculator: A straightforward calculator for computing square roots and visualizing their graphs. Access it at .
- Symbolab Square Root Function Calculator: This tool provides detailed steps for solving square root problems and plotting their curves. Explore it at .
Educational Articles and Tutorials
- Khan Academy: Offers a variety of lessons and practice problems on square root functions and their graphs. Learn more at .
- Math Is Fun: Provides clear explanations and visual aids to help you understand square root functions. Visit for more information.
- Paul's Online Math Notes: Comprehensive notes and examples on the properties and applications of square root functions. Access these resources at .
Research Papers and Advanced Topics
- Square Root Function Analysis: A detailed research paper on the mathematical properties of square root functions and their applications in different fields. Available at .
- Applications of Square Root Functions in Engineering: Explores how square root functions are used in engineering problems. Read more at .
Books and Publications
- Algebra and Trigonometry by Michael Sullivan: A textbook that covers square root functions in depth, with examples and exercises. Check it out at .
- Advanced Engineering Mathematics by Erwin Kreyszig: This book includes advanced discussions on the applications of square root functions in engineering. Find it on .
- Calculus by James Stewart: A comprehensive guide to calculus, including sections on the graphical analysis of functions like square roots. Available on .
Video Tutorials and Lectures
- MIT OpenCourseWare: Free course materials from MIT that include lectures on the mathematical analysis of square root functions. Access these resources at .
- Coursera - Calculus: Single Variable: A course that covers fundamental concepts including square root functions, with video lectures and interactive exercises. Enroll at .
- Numberphile on YouTube: Engaging videos that explain mathematical concepts, including square roots, in an accessible way. Watch their videos at .
Software and Apps
- WolframAlpha: An online computational engine that solves mathematical problems and plots graphs of functions, including square roots. Use it at .
- GeoGebra: A dynamic mathematics software that supports interactive graphing and exploration of square root functions. Download it from .
- Desmos App: The Desmos graphing calculator app offers functionality similar to its online version, ideal for mobile use. Get the app from the .
These resources will provide you with a deeper understanding of square root functions and their graphical representations. Whether you're a student, educator, or professional, these tools and references will enhance your knowledge and application of mathematical concepts.
Video hướng dẫn cách vẽ đồ thị hàm căn bậc hai bằng cách sử dụng biến đổi để thu hút người xem và sửa chính tả.
Vẽ Đồ Thị Hàm Căn Bậc Hai Bằng Cách Sử Dụng Biến Đổi
READ MORE:
Video hướng dẫn cách vẽ đồ thị hàm số căn bậc hai bằng cách sử dụng biến đổi và vẽ điểm để thu hút người xem và sửa chính tả.
Vẽ Đồ Thị Hàm Số Căn Bậc Hai Bằng Cách Sử Dụng Biến Đổi & Vẽ Điểm