Understanding the Square Root of 60: A Comprehensive Guide

The square root of 60 is a number which, when multiplied by itself, equals 60. It is an irrational number, meaning it cannot be expressed as a simple fraction.

Exact and Decimal Form

• Exact Form: \( \sqrt{60} = 2\sqrt{15} \)
• Decimal Form: \( \sqrt{60} \approx 7.7459666924 \)

Simplification Steps

1. Factor 60 into its prime factors: \( 60 = 2^2 \times 3 \times 5 \)
2. Apply the square root to the factorization: \( \sqrt{60} = \sqrt{2^2 \times 15} = 2\sqrt{15} \)

Calculation Examples

Applications

The square root of 60 can be applied in various mathematical contexts, such as geometry and algebra.

FAQs on the Square Root of 60

• What is the value of \( \sqrt{60} \)?
  The value is approximately 7.7459666924.
• Why is \( \sqrt{60} \) irrational?
  Because it cannot be expressed as a ratio of two integers.
• How can \( \sqrt{60} \) be simplified?
  It can be simplified to \( 2\sqrt{15} \).

For more detailed explanations and calculations, you can explore various educational resources online.

The square root of 60 is an important and frequently encountered mathematical value. It is an irrational number, meaning it cannot be expressed as a simple fraction. This irrational nature arises because 60 is not a perfect square, and its prime factors include 3 and 5, which do not form pairs.

The square root of 60 can be expressed in both decimal and radical forms. In decimal form, it is approximately 7.745966692. This value is obtained through methods like long division, which provide a detailed step-by-step approach to finding the square root of a non-perfect square.

In its simplest radical form, the square root of 60 is expressed as \(2\sqrt{15}\). This simplification comes from factoring 60 into \(4 \times 15\) and then taking the square root of each factor. This process involves applying the product rule for radicals: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).

Understanding the square root of 60 is not only critical for solving various mathematical problems but also has practical applications in fields like engineering, physics, and geometry. For instance, it can be used to calculate dimensions in construction projects or determine distances in coordinate geometry.

Overall, the square root of 60, with its unique properties and applications, represents a key concept in both theoretical and applied mathematics.

The square root of 60 can be simplified and expressed in different forms. Here, we will look at both the decimal and radical forms, as well as the method to simplify it.

In its decimal form, the square root of 60 is approximately 7.746. This value is useful for practical calculations where an approximate value is sufficient.

To express the square root of 60 in its simplest radical form, we use the factorization method. The number 60 can be factored into its prime components:

• 60 = 2 × 2 × 3 × 5

Using the property of square roots, where \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\), we can break this down:

• \(\sqrt{60} = \sqrt{2^2 \times 15} = \sqrt{2^2} \times \sqrt{15} = 2\sqrt{15}\)

Thus, the simplest radical form of the square root of 60 is \(2\sqrt{15}\).

The square root of 60 is an irrational number, meaning it cannot be expressed as a simple fraction. This is because 15, one of the factors, is not a perfect square.

To summarize:

• Decimal form: 7.746
• Simplified radical form: \(2\sqrt{15}\)

These forms are used in various mathematical applications, including geometry and algebra, where precise or simplified values are needed.

There are several methods to calculate the square root of 60. Below are the most common methods:

• Prime Factorization Method
  1. First, factorize 60 into its prime factors: \( 60 = 2^2 \times 3 \times 5 \).
  2. Group the prime factors into pairs: \( \sqrt{60} = \sqrt{2^2 \times 3 \times 5} \).
  3. Extract the pairs out of the square root: \( \sqrt{60} = 2\sqrt{15} \).
  4. Thus, the simplified radical form is \( 2\sqrt{15} \).
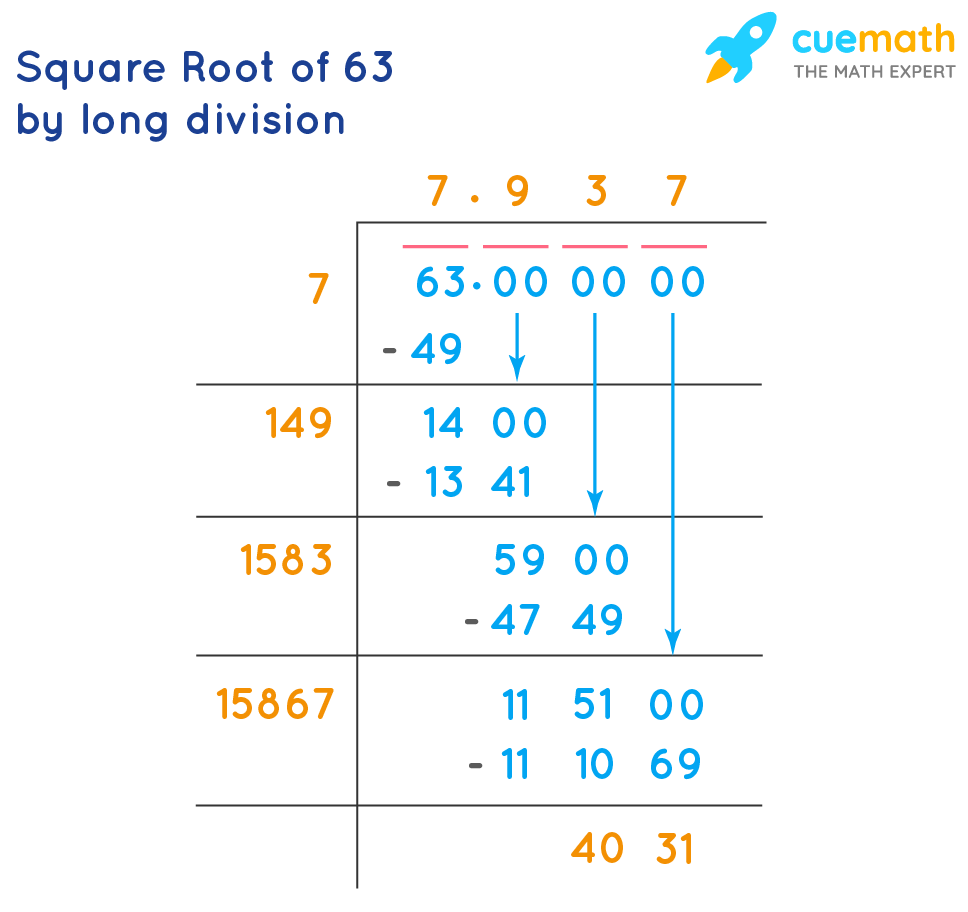
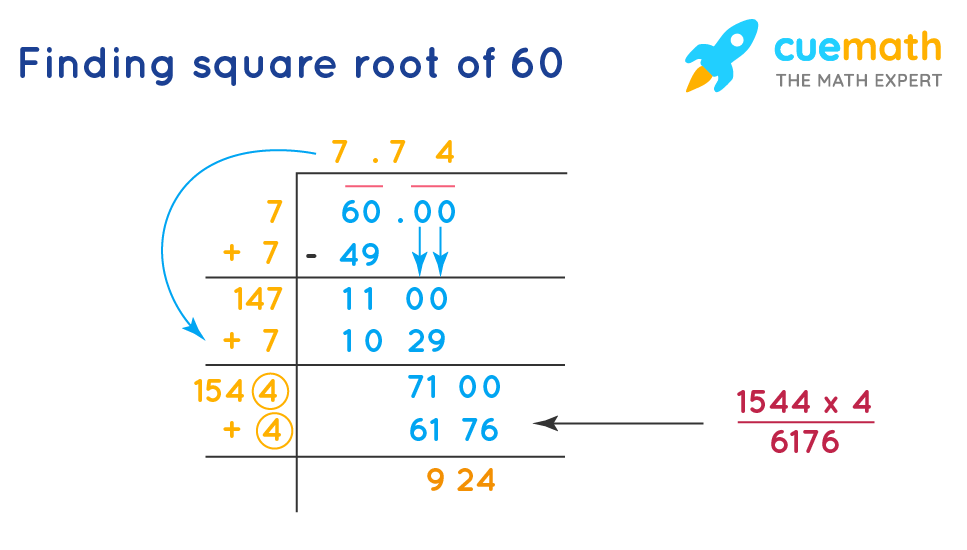
• Long Division Method
  1. Start by grouping the digits in pairs from right to left. For 60, consider 60.00 for more precision.
  2. Find the largest number whose square is less than or equal to 60. In this case, it’s 7 because \( 7^2 = 49 \).
  3. Subtract 49 from 60 to get the remainder 11. Bring down two zeros to get 1100.
  4. Double the divisor (7), making it 14. Find a digit (X) such that \( 14X \times X \leq 1100 \). This gives us 7 because \( 147 \times 7 = 1029 \).
  5. Repeat this process to get a more accurate value, continuing with 7100 and so on. The approximate value up to two decimal places is 7.74.
• Using a Calculator

  The simplest method is to use a scientific calculator:

  • Enter 60 and press the square root (√) button.
  • The display shows approximately 7.745966692, which is the decimal form of the square root of 60.

The square root of 60 is not just a mathematical concept; it has numerous practical applications across various fields. Here are some detailed examples:

Geometry and Architecture

In geometry, the square root of 60 is used to calculate the length of the diagonal of a rectangle or the sides of right-angled triangles. For instance, in architectural design, determining the diagonal of a rectangular floor plan involves calculating the square root of the sum of the squares of its sides. This helps architects and engineers in designing and verifying structures.

Physics and Engineering

In physics, square roots are often used to calculate quantities like velocity, acceleration, and force. For example, the speed of an object in free fall can be derived using the square root of the height from which it falls multiplied by the gravitational constant. In engineering, square roots are used in determining the natural frequency of a structure, which is crucial in ensuring that buildings and bridges can withstand dynamic loads such as wind or traffic.

Statistics and Finance

In statistics, the square root of a number is used to calculate standard deviation, which measures the amount of variation or dispersion in a set of values. This is vital for data analysis and interpreting research results. In finance, the square root of the variance is used to calculate the standard deviation of investment returns, helping investors assess risk and volatility.

Computer Science and Cryptography

Square roots play a significant role in computer science, particularly in algorithms for encryption and security. For instance, cryptographic algorithms often involve calculating large prime numbers and their square roots to create secure keys for encrypting data. This ensures safe transmission of sensitive information over networks.

Everyday Applications

• Navigation: Pilots and sailors use the square root to calculate distances between points on a map, ensuring accurate travel routes.
• Cooking: Adjusting recipes involves scaling ingredients up or down, often using square roots to maintain the correct proportions.
• Photography: In camera settings, the f-number, which controls the aperture size, is related to the square root of the aperture area, influencing the depth of field and exposure.

Overall, the square root of 60 is a versatile number with a wide range of applications that demonstrate the intersection of mathematics with real-world problems and industries.

Here are some frequently asked questions about the square root of 60:

• Why is the square root of 60 considered an irrational number?

The square root of 60 is an irrational number because it cannot be expressed as a fraction of two integers. Its decimal form is non-terminating and non-repeating, approximately equal to 7.745966692.

• What is the simplest radical form of the square root of 60?

The simplest radical form of the square root of 60 is \(2\sqrt{15}\). This is derived from the prime factorization of 60, which is \(2^2 \times 3 \times 5\), allowing us to simplify the square root.

• How can you calculate the square root of 60 using the long division method?

The long division method involves dividing the number into pairs of digits from the decimal point and finding the largest number whose square is less than or equal to the number. This process is repeated for precision. For example, using this method, you approximate the square root of 60 to get closer to 7.745966692.

• Is 60 a perfect square?

No, 60 is not a perfect square because its square root (7.745966692) is not an integer. Perfect squares are numbers like 1, 4, 9, 16, etc., whose square roots are whole numbers.

• What are some real-life applications of the square root of 60?

Real-life applications of the square root of 60 include calculations in geometry, such as finding the diagonal of a rectangle with sides of certain lengths, or in physics, such as determining the magnitude of vectors or in various engineering problems where precise measurements are necessary.

• Can the square root of 60 be simplified further?

The square root of 60 is already in its simplest radical form as \(2\sqrt{15}\). It cannot be simplified further since 15 is not a perfect square.

Understanding the square root of 60 involves several related mathematical concepts that are fundamental to grasping the broader implications of square roots and radicals. Here are some key concepts:

• Irrational Numbers: The square root of 60 is an example of an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal representation is non-repeating and non-terminating.
• Simplifying Radicals: Simplifying radicals involves expressing a square root in its simplest form. For instance, the square root of 60 can be simplified to \(2\sqrt{15}\) by factoring out the largest perfect square factor.
• Properties of Square Roots: Key properties include:
  • \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
  • \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
  • \((\sqrt{a})^2 = a\)
• Radical Equations: These are equations in which the variable appears under a square root. Solving them typically involves isolating the radical on one side and then squaring both sides to eliminate the radical.
• Exponentiation: The square root operation can be seen as raising a number to the power of \( \frac{1}{2} \). For example, \( \sqrt{60} = 60^{\frac{1}{2}} \).
• Perfect Squares: A perfect square is a number that is the square of an integer. Understanding perfect squares helps in simplifying and estimating square roots.
• Complex Numbers: If dealing with negative numbers under a square root, the result is a complex number. For example, \( \sqrt{-60} = i\sqrt{60} \), where \(i\) is the imaginary unit.

Here are some tools and resources related to the square root of 60:

• : Offers a simple online calculator to find the square root of any number, including 60.
• : Provides not only the square root calculation but also shows step-by-step solutions and alternative forms.
• : A straightforward tool for calculating square roots with additional options for precision and rounding.
• : Offers a user-friendly interface with explanations on how square roots are computed.

Exploring the square root of 60 reveals its significance across various disciplines. From its decimal approximation of approximately 7.745966692 to its simplified radical form as 2√15, understanding this value is crucial in mathematics and its applications.

Whether used in calculating areas, distances, or other measurements, the square root of 60 remains a fundamental component in both theoretical studies and practical scenarios. Its presence underscores the pervasive nature of mathematical constants in everyday life.

Further exploration into related concepts such as irrational numbers and radical simplification enhances the appreciation of the square root of 60's role in mathematical frameworks. Online resources and calculators readily facilitate deeper comprehension and application of this essential mathematical value.