Topic square root meaning in math: Square roots are fundamental in mathematics, offering a way to find a number that, when multiplied by itself, yields the original number. This comprehensive guide explores the meaning of square roots, their properties, methods to find them, and their applications in various mathematical contexts, making it an essential resource for students and enthusiasts.
Table of Content
- Understanding the Square Root in Mathematics
- Introduction to Square Roots
- Definition of Square Roots
- Square Root Symbol
- Square Root Formula
- Methods to Find Square Roots
- Prime Factorization Method
- Repeated Subtraction Method
- Long Division Method
- Estimation Method
- Square Roots of Perfect Squares
- Square Root Table
- Square Roots of Decimals
- Square Roots of Negative Numbers
- Square Roots of Complex Numbers
- Square Root Equations
- List of Square Roots
- Solved Problems
- Worksheets
- YOUTUBE: Khám phá khái niệm căn bậc hai với Thầy J. Video này giúp bạn hiểu rõ hơn về căn bậc hai trong toán học và cách áp dụng nó.
Understanding the Square Root in Mathematics
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol √. For example, the square root of 16 is 4, because 4 × 4 = 16. Similarly, -4 is also a square root of 16 since (-4) × (-4) = 16. However, when we use the symbol √, we generally refer to the positive root.
Mathematical Notation
If z is the square root of x, this can be expressed as:
Thus, because 5 × 5 = 25.
Properties of Square Roots
- Every positive number has two square roots: one positive and one negative.
- The square root of 0 is 0.
- The square roots of negative numbers are not real numbers; they are complex numbers.
Calculating Square Roots
Finding the square root of a perfect square is straightforward. For non-perfect squares, the calculation involves estimation or a calculator. For example, the square root of 10 is approximately 3.162, as it lies between 3 × 3 = 9 and 4 × 4 = 16.
Examples
Consider the square root of 9:
and since both 3 × 3 and -3 × -3 equal 9.
Perfect Squares
The first few perfect squares are:
| 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
Square Root Symbol and Usage
The square root symbol (√) is known as the radical. When using this symbol, it refers to the principal (positive) square root.
For example, , because 6 × 6 = 36.
Square Roots of Non-Perfect Squares
To find the square root of a non-perfect square, such as 2, we estimate that it is between 1 and 2. A more precise value is approximately 1.414, which is an irrational number.
Calculators are commonly used to find square roots quickly. For example, the square root button on a calculator will provide the square root of any given number efficiently.
Applications of Square Roots
Square roots are used in various mathematical contexts, including solving quadratic equations and in geometry to find the sides of a right triangle.
For more in-depth information and interactive examples, you can explore resources such as MathIsFun, Byju's, Math.net, and Wolfram MathWorld.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because 4 × 4 = 16. The square root symbol is √, and it typically refers to the positive square root. For instance, √36 = 6. Square roots are fundamental in various mathematical applications, including solving quadratic equations and understanding geometric properties.
In mathematical terms, if x is the square root of y, it can be represented as x = √y, or equivalently, x² = y. This relationship means that finding the square root is essentially the inverse operation of squaring a number.
Square roots can be categorized into perfect and imperfect squares. A perfect square, like 9, has an integer as its square root (√9 = 3). Conversely, an imperfect square, like 7, does not have an integer square root and is often approximated or expressed in a simplified radical form.
Additionally, square roots extend beyond real numbers. The square root of a negative number involves imaginary numbers, denoted by i, where i² = -1. Thus, the square root of -4 is 2i. This concept is crucial in complex number theory.
Understanding square roots is essential for various real-world applications, including engineering, physics, and computer science, where they are used to model and solve problems involving areas, volumes, and rates of change.
Definition of Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. For a given number \( x \), the square root is denoted as \( \sqrt{x} \). Mathematically, if \( z \) is the square root of \( x \), then \( z^2 = x \). This means both \( z \) and \( -z \) are square roots of \( x \) because both satisfy the equation \( z^2 = x \).
The principal square root is the non-negative value of the square root. For instance, the principal square root of 9 is 3, even though -3 is also a square root of 9. In notation, we usually refer to the principal square root when using the radical symbol \( \sqrt{} \).
Square roots have several important properties:
- Non-negative numbers: For any non-negative number \( x \), \( \sqrt{x} \) is also a non-negative number.
- Product property: The square root of a product is the product of the square roots, i.e., \( \sqrt{xy} = \sqrt{x} \cdot \sqrt{y} \) for \( x \geq 0 \) and \( y \geq 0 \).
- Quotient property: The square root of a quotient is the quotient of the square roots, i.e., \( \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} \) for \( x \geq 0 \) and \( y > 0 \).
When dealing with complex numbers, the definition extends such that the square root of a complex number involves both real and imaginary parts, given by the formula:
\[ \sqrt{z} = \sqrt{x + yi} = \pm \left( \sqrt{\frac{|z| + x}{2}} + i \frac{y}{|y|} \sqrt{\frac{|z| - x}{2}} \right) \]
where \( z = x + yi \) and \( |z| \) is the magnitude of \( z \).
Square Root Symbol
The square root symbol, denoted as √, is a fundamental mathematical symbol used to represent the square root of a number. This symbol, also known as the radical symbol, indicates the operation of finding a number which, when multiplied by itself, yields the original number. For instance, the square root of 16 is written as √16, which equals 4, since 4 × 4 = 16.
In mathematical notation, the expression √x is used to denote the square root of x. The number inside the radical symbol is called the radicand. The square root symbol always represents the positive root, also known as the principal square root.
Here are some examples of the square root symbol in use:
- √4 = 2, because 2 × 2 = 4
- √9 = 3, because 3 × 3 = 9
- √25 = 5, because 5 × 5 = 25
In addition to the square root, the radical symbol can be used to represent other roots by placing a small number, called the index, above the symbol. For example, the cube root of 8 is written as and equals 2, as 2 × 2 × 2 = 8.
For digital and web content, the square root symbol can be represented in various formats:
- HTML Code: √
- Unicode: U+221A
- TeX: \sqrt{}
The square root symbol is an essential part of mathematical notation, used in various fields such as algebra, geometry, and calculus to simplify expressions and solve equations.
Square Root Formula
The square root formula is fundamental in mathematics, allowing us to find the square root of a number. The basic formula is:
This formula indicates that the square root of \( x \) is the number that, when squared, equals \( x \). Here are the steps to use this formula:
- Identify the number for which you need to find the square root.
- Express the number as a product of its prime factors, if possible.
- Apply the formula \( \sqrt{x} = x^{\frac{1}{2}} \).
For example, to find the square root of 256:
- Recognize that 256 is a perfect square (16 * 16).
- Apply the formula: \( \sqrt{256} = (16^2)^{\frac{1}{2}} = 16 \).
The square root formula is also applicable in solving various mathematical problems, such as finding the side length of a square when its area is known. For instance:
Given a square carpet with an area of 196 square meters, the side length is found by:
Thus, the perimeter of the carpet would be:
This formula is essential in fields such as geometry, algebra, and beyond, providing a straightforward method to calculate square roots and solve related problems.

Methods to Find Square Roots
There are several methods to find the square roots of numbers. Here, we will discuss four main methods: Prime Factorization Method, Repeated Subtraction Method, Long Division Method, and Estimation Method.
1. Prime Factorization Method
This method involves breaking down a number into its prime factors and then pairing the factors to find the square root.
- Resolve the given number into prime factors.
- Make pairs of similar factors.
- Take the product of one factor from each pair to get the square root.
Example: Find the square root of 81.
81 = 3 × 3 × 3 × 3
√81 = √(3 × 3 × 3 × 3) = 3 × 3 = 9
2. Repeated Subtraction Method
This method uses the sum of the first n odd natural numbers to find the square root.
- Subtract consecutive odd numbers from the given number until you reach zero.
- The number of steps taken to reach zero is the square root.
Example: Find the square root of 121.
121 - 1 = 120
120 - 3 = 117
117 - 5 = 112
112 - 7 = 105
105 - 9 = 96
96 - 11 = 85
85 - 13 = 72
72 - 15 = 57
57 - 17 = 40
40 - 19 = 21
21 - 21 = 0
Steps taken: 11, so √121 = 11
3. Long Division Method
This method involves dividing the number in a manner similar to long division to find the square root.
- Pair the digits of the number from right to left.
- Find the largest number whose square is less than or equal to the leftmost pair.
- Subtract the square of this number from the pair and bring down the next pair.
- Double the quotient and find a new digit for the divisor and quotient that works with the next dividend.
- Repeat until all pairs have been used.
Example: Find the square root of 104976.
10, 49, 76 - Using long division steps, we find √104976 = 324.
4. Estimation Method
This method involves making an educated guess and refining it through trial and error.
- Guess a number and square it.
- If the result is greater than the original number, try a smaller number.
- If the result is less, try a larger number.
- Continue until the exact square root is found.
Example: To find √50, start with 7 (since 7² = 49). Adjust up or down to find the precise value.
Prime Factorization Method
The prime factorization method is a straightforward approach to finding the square root of a number by expressing it as a product of prime factors. This method is particularly useful for perfect squares.
- Start by expressing the number as a product of its prime factors. For example, consider the number 3600:
- \(3600 = 2 \times 2 \times 3 \times 3 \times 10 \times 10\)
- Group the prime factors into pairs of equal factors:
- \(\sqrt{3600} = \sqrt{(2 \times 2) \times (3 \times 3) \times (10 \times 10)}\)
- Take one factor from each pair and multiply them together:
- \(\sqrt{3600} = 2 \times 3 \times 10 = 60\)
- Thus, the square root of 3600 is 60.
Let's consider another example with the number 484:
- Prime factorize 484:
- \(484 = 2 \times 2 \times 11 \times 11\)
- Group the prime factors into pairs:
- \(\sqrt{484} = \sqrt{(2 \times 2) \times (11 \times 11)}\)
- Take one factor from each pair and multiply them together:
- \(\sqrt{484} = 2 \times 11 = 22\)
- Thus, the square root of 484 is 22.
The prime factorization method helps simplify the process of finding square roots, making it easier to handle large numbers systematically.
Repeated Subtraction Method
The repeated subtraction method is a straightforward technique to find the square root of a number by continuously subtracting consecutive odd numbers from the original number until the remainder becomes zero. Here are the detailed steps to understand this method:
- Start with the given number (e.g., 144).
- Subtract the first odd number (1) from the given number (144 - 1 = 143).
- Subtract the next odd number (3) from the result (143 - 3 = 140).
- Continue subtracting the next odd numbers sequentially (5, 7, 9, etc.) from the result of each previous subtraction.
- Repeat the process until the remainder is zero.
- The number of subtractions performed is the square root of the original number.
Example:
To find the square root of 144:
- 144 - 1 = 143
- 143 - 3 = 140
- 140 - 5 = 135
- 135 - 7 = 128
- 128 - 9 = 119
- 119 - 11 = 108
- 108 - 13 = 95
- 95 - 15 = 80
- 80 - 17 = 63
- 63 - 19 = 44
- 44 - 21 = 23
- 23 - 23 = 0
Since we performed 12 subtractions, the square root of 144 is 12. Therefore, \( \sqrt{144} = 12 \).
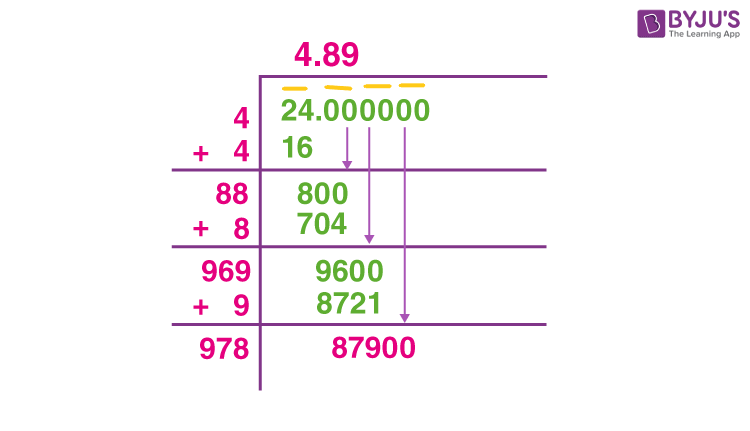
Long Division Method
The Long Division Method is a systematic way to find the square root of a number. Follow these steps to find the square root using this method:
- Pair the Digits: Start from the decimal point (or rightmost digit if there is no decimal). Separate the digits into pairs by placing a bar over each pair. Each pair is called a period.
- Initial Division: Find the largest number whose square is less than or equal to the first period. Write this number as the divisor and the quotient. Subtract the square of this number from the first period and bring down the next period to the right of the remainder.
- Double the Quotient: Double the quotient and write it as the new divisor with a blank space next to it.
- Find the Next Digit: Find a digit to fill the blank in the new divisor such that when multiplied by the same digit, the product is less than or equal to the current dividend. Write this digit in the blank and next to the current quotient. Subtract the product from the current dividend and bring down the next period.
- Repeat: Repeat the process of doubling the quotient, finding the next digit, and subtracting the product until all periods have been brought down.
Example: Finding the square root of 784 using the Long Division Method:
- Pair the Digits: 7|84
- Initial Division: The largest square less than or equal to 7 is 4 (since 2*2=4). Subtract 4 from 7 to get a remainder of 3 and bring down 84.
- Double the Quotient: The quotient is 2, so double it to get 4. Write 4 with a blank: 4_.
- Find the Next Digit: Find a digit to complete 4_ such that the product is ≤ 384. The suitable digit is 6 (since 46*6=276). Subtract 276 from 384 to get a remainder of 108.
- Repeat: Continue the process to get the next digits of the quotient. The quotient obtained is 28, so the square root of 784 is 28.

Estimation Method
The estimation method for finding square roots involves approximating the square root of a number by finding two perfect squares between which the number lies. This method is useful for getting a rough idea of the square root, especially when a calculator is not available. Below are the steps to estimate the square root of a number:
-
Identify the perfect squares: Find the two perfect squares between which the number lies. For example, to estimate the square root of 20, identify that 16 (42) and 25 (52) are the perfect squares between which 20 lies.
-
Estimate the value: Since 20 is closer to 16 than to 25, the square root of 20 will be closer to 4 than to 5. A good initial estimate might be 4.5.
-
Refine the estimate: To refine the estimate, calculate the square of your estimate and see how close it is to the original number. If the estimate squared is too high, lower the estimate; if it is too low, raise the estimate.
- Initial estimate: 4.5
- Square of 4.5: \(4.5^2 = 20.25\) (slightly higher than 20)
- Refine estimate: Try 4.4
- Square of 4.4: \(4.4^2 = 19.36\) (slightly lower than 20)
-
Iterate as needed: Continue refining your estimate by testing values between your previous estimates until you achieve the desired level of accuracy. For example, between 4.4 and 4.5, you might try 4.45:
- Estimate: 4.45
- Square of 4.45: \(4.45^2 = 19.8025\) (still slightly lower than 20)
- Try 4.46: \(4.46^2 = 19.8916\)
- Try 4.47: \(4.47^2 = 19.9809\) (very close to 20)
-
Conclude the estimation: Once the squared value is close enough to the original number, you can conclude your estimation. For example, since \(4.47^2\) is very close to 20, you can estimate that \(\sqrt{20} \approx 4.47\).
The estimation method is a practical technique for approximating square roots, especially useful when perfect accuracy is not required, or when tools like calculators are not available.
Square Roots of Perfect Squares
Perfect squares are numbers that are the product of an integer multiplied by itself. The square root of a perfect square is always an integer. Here are some examples of perfect squares and their square roots:
- 1 is a perfect square, and its square root is \( \sqrt{1} = 1 \).
- 4 is a perfect square, and its square root is \( \sqrt{4} = 2 \).
- 9 is a perfect square, and its square root is \( \sqrt{9} = 3 \).
- 16 is a perfect square, and its square root is \( \sqrt{16} = 4 \).
- 25 is a perfect square, and its square root is \( \sqrt{25} = 5 \).
- 36 is a perfect square, and its square root is \( \sqrt{36} = 6 \).
- 49 is a perfect square, and its square root is \( \sqrt{49} = 7 \).
- 64 is a perfect square, and its square root is \( \sqrt{64} = 8 \).
- 81 is a perfect square, and its square root is \( \sqrt{81} = 9 \).
- 100 is a perfect square, and its square root is \( \sqrt{100} = 10 \).
The pattern continues indefinitely. Recognizing these patterns is useful in various mathematical computations, including solving quadratic equations and simplifying radical expressions.
Here is a table of perfect squares from 1 to 15:
| Number | Perfect Square | Square Root |
|---|---|---|
| 1 | 1 | \( \sqrt{1} = 1 \) |
| 2 | 4 | \( \sqrt{4} = 2 \) |
| 3 | 9 | \( \sqrt{9} = 3 \) |
| 4 | 16 | \( \sqrt{16} = 4 \) |
| 5 | 25 | \( \sqrt{25} = 5 \) |
| 6 | 36 | \( \sqrt{36} = 6 \) |
| 7 | 49 | \( \sqrt{49} = 7 \) |
| 8 | 64 | \( \sqrt{64} = 8 \) |
| 9 | 81 | \( \sqrt{81} = 9 \) |
| 10 | 100 | \( \sqrt{100} = 10 \) |
| 11 | 121 | \( \sqrt{121} = 11 \) |
| 12 | 144 | \( \sqrt{144} = 12 \) |
| 13 | 169 | \( \sqrt{169} = 13 \) |
| 14 | 196 | \( \sqrt{196} = 14 \) |
| 15 | 225 | \( \sqrt{225} = 15 \) |
Understanding perfect squares helps in various mathematical contexts and provides a foundation for more advanced topics such as algebra and calculus.
Square Root Table
A square root table is a handy reference for finding the square roots of perfect squares and other numbers. Below is a table that lists the square roots of numbers from 1 to 20 and some additional commonly used numbers.
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| 6 | \(\sqrt{6} \approx 2.449\) |
| 7 | \(\sqrt{7} \approx 2.646\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 9 | \(\sqrt{9} = 3\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
| 11 | \(\sqrt{11} \approx 3.317\) |
| 12 | \(\sqrt{12} \approx 3.464\) |
| 13 | \(\sqrt{13} \approx 3.606\) |
| 14 | \(\sqrt{14} \approx 3.742\) |
| 15 | \(\sqrt{15} \approx 3.873\) |
| 16 | \(\sqrt{16} = 4\) |
| 17 | \(\sqrt{17} \approx 4.123\) |
| 18 | \(\sqrt{18} \approx 4.243\) |
| 19 | \(\sqrt{19} \approx 4.359\) |
| 20 | \(\sqrt{20} \approx 4.472\) |
| 25 | \(\sqrt{25} = 5\) |
| 36 | \(\sqrt{36} = 6\) |
| 49 | \(\sqrt{49} = 7\) |
| 64 | \(\sqrt{64} = 8\) |
| 81 | \(\sqrt{81} = 9\) |
| 100 | \(\sqrt{100} = 10\) |
This table provides a quick reference to help you find the square roots of numbers, especially useful for students and professionals dealing with mathematics regularly.
Square Roots of Decimals
Finding the square root of a decimal number involves a process similar to finding the square root of a whole number, but it can be more complex due to the presence of decimal points. Here, we will go through a step-by-step method to estimate and calculate the square root of decimal numbers.
Step-by-Step Estimation Method
- Identify Perfect Squares:
First, identify the perfect squares that are closest to the given decimal. For example, for a decimal like 0.64, the closest perfect squares are 0.25 (since 0.52 = 0.25) and 1 (since 12 = 1).
- Initial Approximation:
Find an initial approximation of the square root by determining where the decimal falls between the perfect squares. For instance, since 0.64 is between 0.25 and 1, its square root should be between 0.5 and 1.
- Refine the Approximation:
Use a method such as averaging or iterative guessing to refine the approximation. For example, if we start with a guess of 0.8 (since 0.82 = 0.64), we find that the square root of 0.64 is 0.8.
Long Division Method
The long division method is another systematic approach to finding the square root of decimals. Here's how it works:
- Pair the Digits:
Starting from the decimal point, pair the digits of the number. For instance, for 0.64, pair it as 0.64.
- Find the Largest Square:
Find the largest square less than or equal to the first pair (0 in this case), and write it as the first digit of the quotient. The square root of 0 is 0.
- Double the Quotient:
Double the quotient (0), and use it as the new divisor.
- Bring Down Pairs:
Bring down the next pair of digits (64), and repeat the division process with the new divisor (0).
- Calculate the Quotient:
The quotient obtained will be the square root. For 0.64, the final quotient is 0.8, hence the square root of 0.64 is 0.8.
Example Calculation
Consider finding the square root of 0.25:
- Identify the closest perfect squares: 0 and 1 (0.52 = 0.25).
- Initial approximation: 0.5 (since 0.52 = 0.25).
- Refinement: Since the square root of 0.25 is exactly 0.5, no further refinement is needed.
Properties of Square Roots of Decimals
- Square roots of decimals can be either terminating or repeating decimals.
- The square root of a number less than 1 is always greater than the number itself but less than 1.
- Precision can be increased by using more decimal places in the approximation process.

Square Roots of Negative Numbers
In mathematics, the concept of square roots extends beyond positive numbers and includes negative numbers as well. However, the square roots of negative numbers are not real numbers; instead, they belong to the set of complex numbers.
The square root of a negative number can be expressed using the imaginary unit \(i\), which is defined as the square root of -1. This leads to the following general formula:
\[ \sqrt{-a} = \sqrt{a} \cdot i \]
where \(a\) is a positive real number. Here are some steps to understand and compute the square roots of negative numbers:
- Identify the negative number for which you need to find the square root. Let's say the number is \(-a\).
- Write the negative number in terms of \(i\). For example, \(\sqrt{-9}\) can be written as \(\sqrt{9 \cdot -1}\).
- Simplify the expression using the property of square roots:
\[ \sqrt{-9} = \sqrt{9 \cdot -1} = \sqrt{9} \cdot \sqrt{-1} = 3i \]
Here are some examples of square roots of negative numbers:
- \(\sqrt{-1} = i\)
- \(\sqrt{-4} = 2i\)
- \(\sqrt{-16} = 4i\)
In general, for any positive real number \(a\), the square root of \(-a\) will be \( \sqrt{a} \cdot i \).
This concept is crucial in the study of complex numbers, which are used in various fields such as engineering, physics, and mathematics to solve equations that do not have real solutions.
Square Roots of Complex Numbers
Square roots of complex numbers extend the concept of square roots to the complex plane. A complex number is expressed in the form \( z = a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit (\( i^2 = -1 \)). The square root of a complex number can be found using algebraic methods.
To find the square root of a complex number \( z = a + bi \), follow these steps:
- Express the complex number in polar form: \[ z = re^{i\theta} \] where \( r = \sqrt{a^2 + b^2} \) is the magnitude and \( \theta = \tan^{-1} \left(\frac{b}{a}\right) \) is the argument of the complex number.
- Use the polar form to find the square roots: \[ \sqrt{z} = \sqrt{r} e^{i\frac{\theta}{2}} \] This will give two values, as the square root function in the complex plane has two values: \[ \sqrt{z} = \sqrt{r} \left( \cos\left(\frac{\theta}{2}\right) + i \sin\left(\frac{\theta}{2}\right) \right) \] and \[ -\sqrt{r} \left( \cos\left(\frac{\theta}{2}\right) + i \sin\left(\frac{\theta}{2}\right) \right) \]
Here is a step-by-step example to illustrate:
Let's find the square roots of the complex number \( z = 3 + 4i \).
- Calculate the magnitude \( r \): \[ r = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Determine the argument \( \theta \): \[ \theta = \tan^{-1} \left(\frac{4}{3}\right) \] For simplicity, let's approximate \( \theta \approx 0.93 \) radians.
- Find the square root in polar form: \[ \sqrt{z} = \sqrt{5} e^{i \frac{0.93}{2}} = \sqrt{5} \left( \cos\left(0.465\right) + i \sin\left(0.465\right) \right) \] Using approximate values: \[ \sqrt{z} = \sqrt{5} \left( 0.894 + i \cdot 0.447 \right) \approx 2.236 \left( 0.894 + i \cdot 0.447 \right) \] \[ \sqrt{z} \approx 2 + i \] The other root is: \[ -\sqrt{5} \left( 0.894 + i \cdot 0.447 \right) \approx -2 - i \] Hence, the square roots of \( 3 + 4i \) are approximately \( 2 + i \) and \( -2 - i \).
Square Root Equations
Square root equations are equations that involve the square root of a variable. Solving these equations often requires isolating the square root term and then squaring both sides of the equation to eliminate the square root. Here is a detailed step-by-step process to solve square root equations:
-
Isolate the Square Root: Ensure that the square root term is by itself on one side of the equation.
Example: \( \sqrt{x + 3} = 5 \)
-
Square Both Sides: Eliminate the square root by squaring both sides of the equation.
Example: \( (\sqrt{x + 3})^2 = 5^2 \)
This simplifies to: \( x + 3 = 25 \)
-
Solve the Resulting Equation: Solve the equation obtained after squaring both sides.
Example: \( x + 3 = 25 \)
Solve for \( x \): \( x = 25 - 3 \)
Therefore, \( x = 22 \)
-
Check for Extraneous Solutions: Substitute the solution back into the original equation to verify it.
Example: Substitute \( x = 22 \) back into the original equation: \( \sqrt{22 + 3} = 5 \)
Since \( \sqrt{25} = 5 \), the solution \( x = 22 \) is correct.
In general, solving square root equations involves these core steps, but additional complexities can arise if there are multiple square root terms or other operations involved. Below are some more examples:
Example 1:
Solve \( \sqrt{2x + 3} = 7 \)
- Isolate the square root: \( \sqrt{2x + 3} = 7 \)
- Square both sides: \( (\sqrt{2x + 3})^2 = 7^2 \)
- Simplify: \( 2x + 3 = 49 \)
- Solve for \( x \): \( 2x = 46 \) ⟹ \( x = 23 \)
- Check the solution: \( \sqrt{2(23) + 3} = \sqrt{46 + 3} = \sqrt{49} = 7 \)
Example 2:
Solve \( \sqrt{x - 1} + 2 = 6 \)
- Isolate the square root: \( \sqrt{x - 1} = 6 - 2 \) ⟹ \( \sqrt{x - 1} = 4 \)
- Square both sides: \( (\sqrt{x - 1})^2 = 4^2 \)
- Simplify: \( x - 1 = 16 \)
- Solve for \( x \): \( x = 17 \)
- Check the solution: \( \sqrt{17 - 1} + 2 = \sqrt{16} + 2 = 4 + 2 = 6 \)
These steps can be used to solve a variety of square root equations. It's essential to remember to check for extraneous solutions, as squaring both sides can sometimes introduce solutions that do not satisfy the original equation.
List of Square Roots
Square roots are values that, when multiplied by themselves, yield the original number. Here is a list of square roots for perfect squares from 1 to 15:
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| 6 | \(\sqrt{6} \approx 2.449\) |
| 7 | \(\sqrt{7} \approx 2.646\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 9 | \(\sqrt{9} = 3\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
| 11 | \(\sqrt{11} \approx 3.317\) |
| 12 | \(\sqrt{12} \approx 3.464\) |
| 13 | \(\sqrt{13} \approx 3.606\) |
| 14 | \(\sqrt{14} \approx 3.742\) |
| 15 | \(\sqrt{15} \approx 3.873\) |
Square roots of perfect squares are integers, while those of non-perfect squares are irrational numbers, often approximated to a few decimal places.

Solved Problems
In this section, we will explore some solved problems related to square roots. Each problem is followed by a step-by-step solution to help you understand the process.
Problem 1: Finding the Square Root of a Perfect Square
Find the square root of 144.
- Recognize that 144 is a perfect square.
- Write 144 as a product of its prime factors: \( 144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3 \).
- Pair the prime factors: \( (2 \times 2) \times (2 \times 2) \times (3 \times 3) \).
- Select one number from each pair: \( 2 \times 2 \times 3 = 12 \).
- Thus, \( \sqrt{144} = 12 \).
Problem 2: Solving an Equation with Square Roots
Solve the equation \( \sqrt{2x + 3} = 10 \).
- Square both sides of the equation to remove the square root: \( (\sqrt{2x + 3})^2 = 10^2 \).
- This simplifies to \( 2x + 3 = 100 \).
- Subtract 3 from both sides: \( 2x = 97 \).
- Divide both sides by 2: \( x = \frac{97}{2} = 48.5 \).
Problem 3: Square Root of a Fraction
Find the square root of \( \frac{9}{16} \).
- Recognize that \( \frac{9}{16} \) is a fraction where both numerator and denominator are perfect squares.
- Write the square root of the fraction as the fraction of the square roots: \( \sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} \).
- Simplify the square roots: \( \sqrt{9} = 3 \) and \( \sqrt{16} = 4 \).
- Thus, \( \sqrt{\frac{9}{16}} = \frac{3}{4} \).
Problem 4: Solving a Quadratic Equation by Taking Square Roots
Solve the equation \( x^2 = 49 \).
- Take the square root of both sides: \( \sqrt{x^2} = \sqrt{49} \).
- This simplifies to \( x = \pm 7 \).
- Thus, the solutions are \( x = 7 \) and \( x = -7 \).
Problem 5: Simplifying a Square Root Expression
Simplify \( \sqrt{50} \).
- Write 50 as a product of its prime factors: \( 50 = 2 \times 5 \times 5 \).
- Recognize that \( 5 \times 5 \) is a perfect square: \( \sqrt{50} = \sqrt{2 \times 25} \).
- Separate the square root: \( \sqrt{50} = \sqrt{2} \times \sqrt{25} \).
- Simplify the square roots: \( \sqrt{25} = 5 \).
- Thus, \( \sqrt{50} = 5\sqrt{2} \).
Worksheets
Here are some engaging and educational worksheets to help students practice and master the concept of square roots:
- Finding Square Roots of Perfect Squares
-
These worksheets focus on finding the square roots of perfect squares, which are integers whose square roots are also integers. This helps in building a strong foundation for more complex problems.
-
- Square Roots of Non-Perfect Squares
-
Worksheets designed to practice finding square roots of non-perfect squares. These problems often require simplification to the simplest radical form.
-
- Simplifying Square Roots
-
These exercises help students learn to simplify square roots, including those involving negative numbers and imaginary numbers.
-
- Square Root Tables
-
Printable square root tables provide a handy reference for students to quickly find the square roots of common numbers.
-
- Square Root Equations
-
Worksheets that involve solving equations that include square roots, helping students apply their knowledge in more complex scenarios.
-
These worksheets are designed to cater to students from 6th grade to 8th grade, covering a range of difficulty levels to suit different learning needs. They are excellent for classroom practice, homework assignments, or additional practice at home.
Khám phá khái niệm căn bậc hai với Thầy J. Video này giúp bạn hiểu rõ hơn về căn bậc hai trong toán học và cách áp dụng nó.
Căn Bậc Hai Là Gì? | Toán Học Với Thầy J
READ MORE:
Khám phá khái niệm căn bậc hai với video hấp dẫn dành cho trẻ em. Hiểu rõ hơn về ý nghĩa của căn bậc hai trong toán học.
CĂN BẬC HAI 🚀 Căn Bậc Hai Là Gì? 👨🏻🚀 Toán Học Cho Trẻ Em