Topic square root math: Square root math is a fundamental concept in mathematics, offering critical insights into various mathematical operations and real-life applications. This comprehensive guide covers everything from basic definitions and properties to advanced techniques and historical context, ensuring a thorough understanding of square roots for learners of all levels.
Table of Content
- Understanding Square Roots
- Introduction to Square Roots
- Definition and Basic Concepts
- Square Roots of Perfect Squares
- Calculating Square Roots
- Methods for Finding Square Roots
- Prime Factorization Method
- Long Division Method
- Estimation and Approximation Techniques
- Using a Calculator to Find Square Roots
- Square Roots in Algebra
- Square Roots and Exponents
- Graphing Square Root Functions
- Square Roots in Geometry
- Applications of Square Roots in Real Life
- Common Mistakes and Misconceptions
- Advanced Topics in Square Roots
- Historical Background of Square Roots
- Famous Mathematicians and Their Contributions
- YOUTUBE: Video 'Căn Bậc Hai Là Gì?' của thầy J giải thích khái niệm căn bậc hai và cách tính toán đơn giản để giúp học sinh nắm vững kiến thức.
Understanding Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. The square root is denoted by the radical symbol √. For example, the square root of 16 is 4, because 4 × 4 = 16.
Definition
The square root of a number x is written as √x. Mathematically, if z is the square root of x, then:
Properties of Square Roots
- Every positive number has two square roots: one positive and one negative. For instance, the square roots of 9 are 3 and -3.
- Square roots of negative numbers involve imaginary numbers. For example, the square root of -1 is denoted as i, where i2 = -1.
Examples of Simplifying Square Roots
- Simplify √27:
√27 = √(9 × 3) = √9 × √3 = 3√3
- Simplify √8:
√8 = √(4 × 2) = √4 × √2 = 2√2
- Simplify √144:
√144 = √(12 × 12) = 12
Square Roots of Non-Perfect Squares
Calculating the square root of non-perfect squares often results in irrational numbers. For instance, the square root of 2 is approximately 1.41421. These numbers cannot be expressed as a simple fraction and have infinite non-repeating decimal parts.
Solving Equations Involving Square Roots
To solve equations involving square roots, you can square both sides of the equation to eliminate the square root. For example:
Solve √(2x + 3) = 10:
Square both sides:
2x + 3 = 102
2x + 3 = 100
2x = 97
x = 48.5
Table of Squares and Square Roots
| Number | Square | Square Root |
|---|---|---|
| 4 | 16 | 2 |
| 9 | 81 | 3 |
| 16 | 256 | 4 |
| 25 | 625 | 5 |
Algorithms for Finding Square Roots
There are several algorithms for approximating square roots, such as Newton's iteration:
Conclusion
Understanding square roots is fundamental in mathematics, providing a basis for solving equations and simplifying expressions. Recognizing perfect squares and applying the properties of square roots can simplify many mathematical problems.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, crucial for understanding various mathematical operations and applications. A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). In other words, it is a value that, when multiplied by itself, gives the original number. The symbol for square root is \( \sqrt{} \).
For example:
- The square root of 16 is 4, because \( 4 \times 4 = 16 \).
- The square root of 25 is 5, because \( 5 \times 5 = 25 \).
Square roots can be both positive and negative since both \( 3^2 \) and \( (-3)^2 \) equal 9. Thus, \( \sqrt{9} = \pm3 \).
Here are some key properties of square roots:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), for \( b \neq 0 \)
- \( (\sqrt{a})^2 = a \)
- \( \sqrt{a^2} = |a| \)
Square roots are used extensively in various fields such as geometry, algebra, and calculus. For example, in geometry, the Pythagorean theorem uses square roots to determine the length of the sides of a right triangle.
| Number | Square Root | Calculation |
| 4 | 2 | \( \sqrt{4} = 2 \) |
| 9 | 3 | \( \sqrt{9} = 3 \) |
| 16 | 4 | \( \sqrt{16} = 4 \) |
Understanding square roots is essential for solving quadratic equations, working with exponents, and analyzing functions in advanced mathematics. This guide will explore these topics in detail, providing you with a thorough understanding of square roots and their applications.
Definition and Basic Concepts
The square root of a number is a value that, when multiplied by itself, produces the original number. If \( x \) is the original number, then its square root is denoted as \( \sqrt{x} \), and it satisfies the equation \( (\sqrt{x})^2 = x \).
For example:
- \( \sqrt{9} = 3 \) because \( 3^2 = 9 \)
- \( \sqrt{25} = 5 \) because \( 5^2 = 25 \)
Key points to understand about square roots include:
- Positive and Negative Roots: Each positive number \( x \) has two square roots: a positive root \( \sqrt{x} \) and a negative root \( -\sqrt{x} \).
- Zero: The square root of 0 is 0, i.e., \( \sqrt{0} = 0 \).
- Non-Negative Numbers: Square roots are defined for non-negative numbers in the set of real numbers.
Some important properties of square roots are:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), for \( b \neq 0 \)
- \( (\sqrt{a})^2 = a \)
- \( \sqrt{a^2} = |a| \)
Below is a table of some common numbers and their square roots:
| Number | Square Root | Calculation |
| 1 | 1 | \( \sqrt{1} = 1 \) |
| 4 | 2 | \( \sqrt{4} = 2 \) |
| 9 | 3 | \( \sqrt{9} = 3 \) |
| 16 | 4 | \( \sqrt{16} = 4 \) |
Square roots are foundational in various mathematical areas, including algebra, geometry, and calculus. Understanding these basic concepts is essential for further exploration of mathematical principles and applications.
Square Roots of Perfect Squares
A perfect square is a number that is the square of an integer. For example, 1, 4, 9, 16, 25, 36, and so on are perfect squares because they can be written as \(1^2\), \(2^2\), \(3^2\), \(4^2\), \(5^2\), \(6^2\), etc.
The square root of a perfect square is always an integer. For instance, the square root of 25 is 5 because \(5^2 = 25\). Similarly, the square root of 36 is 6 because \(6^2 = 36\).
Here is a table showing some perfect squares and their square roots:
| Perfect Square | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Notice the pattern that emerges: if \( n \) is an integer, then \( n^2 \) is a perfect square and the square root of \( n^2 \) is \( n \).
Understanding perfect squares and their square roots is essential in solving many mathematical problems, including those involving quadratic equations and simplifying radicals.
Here are some key properties of square roots of perfect squares:
- The square root of a perfect square is always a whole number.
- If \( n \) is a positive integer, then the principal (positive) square root of \( n^2 \) is \( n \).
- Square roots are inverse operations to squaring a number.
In summary, recognizing and calculating the square roots of perfect squares are fundamental skills in mathematics, aiding in various computational and algebraic tasks.
Calculating Square Roots
Calculating square roots can be approached in various ways, from simple estimation techniques to precise methods using algorithms. Here are several methods for calculating square roots:
1. Estimation Method
This method involves finding two perfect squares between which the number lies and estimating the square root.
- Identify two perfect squares between which the number falls.
- Estimate the square root as a value between these two numbers.
- Refine the estimate by averaging and checking the square of the estimate.
2. Prime Factorization Method
This method is useful for finding the square roots of perfect squares.
- Factorize the number into its prime factors.
- Group the prime factors into pairs.
- Take one factor from each pair and multiply them to get the square root.
For example, to find the square root of 144:
- 144 = 2 × 2 × 2 × 2 × 3 × 3
- Group into pairs: (2 × 2), (2 × 2), (3 × 3)
- Take one from each pair: 2, 2, and 3
- Multiply them: 2 × 2 × 3 = 12
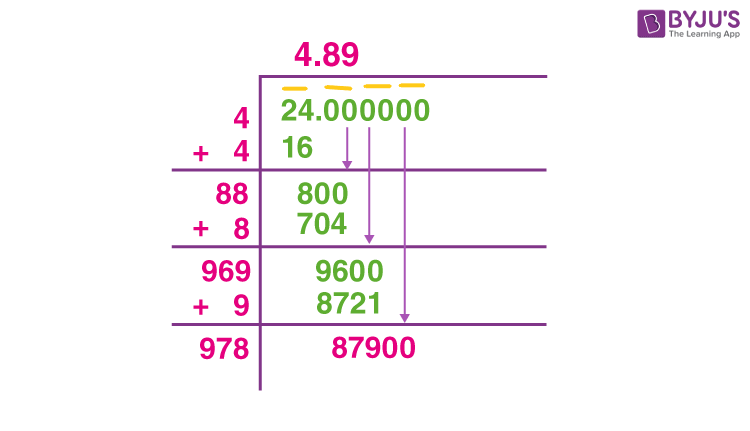
3. Long Division Method
This method is similar to the long division process used for arithmetic and provides an exact value for the square root.
- Separate the number into pairs of digits starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair or single digit.
- Subtract the square of this number from the first pair and bring down the next pair.
- Double the number found so far and find a new digit to append, such that the product of the new number and this digit is less than or equal to the current remainder.
- Repeat the process until all pairs are processed.
4. Using a Calculator
Modern calculators provide a quick and accurate way to find square roots.
- Turn on the calculator.
- Enter the number for which you need to find the square root.
- Press the square root button (√).
- Read the displayed result.
Example Calculation
Let's calculate the square root of 50 using estimation:
- 49 < 50 < 64 (since 7² = 49 and 8² = 64)
- Estimate: 7.5 (between 7 and 8)
- Refinement: (7.5 + 7.1) / 2 = 7.3 (if the initial estimate was closer to 7.1)
- Continue refining until a satisfactory level of precision is achieved.

Methods for Finding Square Roots
There are several methods for finding the square root of a number. Below are some commonly used techniques:
- Estimation Method: Approximate the square root by finding a number whose square is close to the given number.
- Prime Factorization Method: Factorize the number into prime factors and take the square roots of the factors.
- Long Division Method: Similar to long division, this method involves a step-by-step process to find the square root.
- Babylonian Method: An iterative method that repeatedly averages an initial guess with the original number divided by the guess.
- Newton's Method: Uses calculus to approximate the square root based on a function's tangent line.
- Using a Calculator: Modern calculators provide a quick and accurate way to find square roots.
Each method has its advantages depending on the context and required precision.
Prime Factorization Method
The prime factorization method involves breaking down a number into its prime factors to find its square root.
- Step 1: Write the number as a product of prime factors.
- Step 2: Pair up the factors into square roots.
- Step 3: Take one factor from each pair.
Long Division Method
The long division method is a systematic approach to find the square root of a number through repeated subtraction.
- Step 1: Group the number into pairs of digits, starting from the decimal point if necessary.
- Step 2: Find the largest integer whose square is less than or equal to the first group of digits.
- Step 3: Subtract the square of this integer from the group and bring down the next pair of digits.
- Step 4: Double the quotient obtained so far, and guess the next digit.
- Step 5: Repeat steps 3 and 4 until the desired precision is reached.
Estimation and Approximation Techniques
Estimating and approximating square roots involves methods to find a close value without exact calculation.
- Method of Averages: Take two numbers, one slightly less and one slightly more than the square root, and average them.
- Linear Interpolation: Use the slope of the function near the desired square root to estimate its value.
- Geometric Mean: For numbers near perfect squares, use the geometric mean of the endpoints.
- Using Tables: Refer to precomputed tables of square roots for quick reference and estimation.
- Iterative Techniques: Apply iterative methods like Newton's method to improve the approximation iteratively.

Using a Calculator to Find Square Roots
Modern calculators provide a quick and accurate method to find square roots using built-in functions.
- Step 1: Enter the number whose square root you want to find using the numeric keypad.
- Step 2: Locate the square root function on the calculator, often denoted by √ or "sqrt".
- Step 3: Press the square root function key. The calculator will display the square root of the entered number.
- Step 4: Verify the result by squaring the displayed value to ensure accuracy.
- Step 5: Some calculators offer additional features like storing results or performing calculations with the square root directly.
Square Roots in Algebra
Square roots play a crucial role in algebra, particularly in solving quadratic equations and understanding their properties. Here’s a detailed exploration:
- Quadratic Equations: A quadratic equation in the standard form \( ax^2 + bx + c = 0 \) often involves square roots when solving for \( x \). The solutions \( x \) can be found using the quadratic formula:
- Discriminant: The expression \( \Delta = b^2 - 4ac \) within the quadratic formula determines the nature of the roots:
- If \( \Delta > 0 \), the equation has two distinct real roots.
- If \( \Delta = 0 \), the equation has one real root (a repeated root).
- If \( \Delta < 0 \), the equation has two complex roots.
- Completing the Square: This method, used to solve quadratic equations, often involves taking square roots. By manipulating the equation to a form where a perfect square is on one side, one can solve for \( x \).
- Vertex Form: Expressing a quadratic equation in vertex form \( y = a(x-h)^2 + k \) also involves square roots, as the vertex coordinates \( (h, k) \) are derived from \( h = -\frac{b}{2a} \) and \( k = \frac{b^2 - 4ac}{4a} \).
- Imaginary Numbers: When the discriminant is negative, the roots involve imaginary numbers, represented as \( \sqrt{-1} = i \). Thus, solutions may include terms like \( \sqrt{-\Delta} = \sqrt{-(b^2 - 4ac)} = \sqrt{4ac - b^2} \cdot i \).
\[ x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}} \]
Square Roots and Exponents
Understanding the relationship between square roots and exponents is essential in mathematics, especially when dealing with expressions involving radicals. Here are the key points:
- Square Root as Fractional Exponent: The square root of a number \( \sqrt{a} \) can be expressed as an exponent: \( \sqrt{a} = a^{1/2} \).
- Exponentiation and Square Roots: For any non-negative number \( a \), \( \sqrt{a^2} = |a| \), which shows the relationship between squaring and taking square roots.
- Radical Properties: Understanding that \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \) for non-negative numbers \( a \) and \( b \), and \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) when \( b \neq 0 \).
- Exponent Rules: Applying exponent rules, \( (a^m)^n = a^{mn} \), helps simplify expressions involving square roots and exponents.
- Example Problem: Simplify \( \sqrt{x^4} \):
- Express as an exponent: \( \sqrt{x^4} = (x^4)^{1/2} \).
- Apply exponent rule: \( (x^4)^{1/2} = x^{4 \cdot 1/2} \).
- Simplify exponent: \( x^{4 \cdot 1/2} = x^2 \).
- Conclusion: \( \sqrt{x^4} = x^2 \).
Graphing Square Root Functions
Graphing square root functions involves understanding their basic shape and transformations. Here’s how you can graph a square root function:
- Basic Function: The basic square root function is \( y = \sqrt{x} \), which starts from the point \( (0,0) \) and extends to the right, showing only the non-negative values of \( x \).
- Key Points: Plot points like \( (1, 1), (4, 2), (9, 3) \) to understand the pattern of the function.
- Domain and Range: The domain of \( y = \sqrt{x} \) is \( x \geq 0 \) and the range is \( y \geq 0 \).
- Transformations: Apply transformations such as shifts, stretches, and reflections to the basic function. For example, \( y = \sqrt{x - 2} \) shifts the graph 2 units to the right.
- Graphing Steps:
- Plot the basic points of \( y = \sqrt{x} \).
- Apply any transformations by adjusting the \( x \) values accordingly.
- Draw the graph smoothly connecting the points and reflecting any transformations.
- Example Graph: Graph the function \( y = \sqrt{x + 3} - 2 \):
- Shift 3 units left due to \( x + 3 \).
- Shift 2 units down due to \( -2 \).
- Start graphing from \( (-3, -2) \) and plot additional points to depict the transformed function.

Square Roots in Geometry
In geometry, square roots are often used to calculate distances, areas, and other measurements involving squares and rectangles. Here’s how square roots are applied:
- Distance Formula: The distance between two points \( (x_1, y_1) \) and \( (x_2, y_2) \) in a coordinate plane is given by \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). This formula derives from the Pythagorean theorem.
- Area of a Square: The side length \( s \) of a square with area \( A \) is calculated as \( s = \sqrt{A} \).
- Diagonal of a Square: The diagonal \( d \) of a square with side length \( s \) is \( d = s\sqrt{2} \).
- Rectangle Properties: For a rectangle with length \( l \) and width \( w \):
- Diagonal \( d = \sqrt{l^2 + w^2} \).
- Area \( A = lw \).
- Perimeter \( P = 2(l + w) \).
- Applications: Square roots are crucial in practical geometric applications such as construction, architecture, and engineering to ensure accurate measurements and calculations.
- Example Problem: Calculate the diagonal of a rectangle with length \( 5 \) units and width \( 12 \) units:
- Apply the formula: \( d = \sqrt{5^2 + 12^2} \).
- Calculate: \( d = \sqrt{25 + 144} = \sqrt{169} = 13 \) units.
- Conclusion: The diagonal of the rectangle is \( 13 \) units.
Applications of Square Roots in Real Life
Square roots have numerous practical applications in everyday life and various fields. Here are some notable examples:
- Engineering and Construction: Square roots are used to calculate dimensions, distances, and forces in structures, ensuring stability and safety.
- Finance and Economics: In financial modeling, square roots are employed in formulas such as the standard deviation to measure risk and volatility.
- Physics: Square roots appear in formulas related to energy, wave propagation, and signal processing, aiding in understanding natural phenomena.
- Medicine: Medical imaging techniques like MRI and CT scans use square roots in algorithms to enhance image clarity and accuracy.
- Navigation: GPS systems utilize square roots to determine distances between locations and optimize routes for travel.
- Statistics: Square roots are integral in statistical analysis, particularly in calculating means, deviations, and correlations.
- Computer Graphics: Algorithms for rendering and displaying images often involve square roots to determine pixel intensities and positions.
- Education: Square roots are taught in schools as fundamental mathematical concepts, helping students understand numbers and relationships.
- Environmental Science: Square roots are used in environmental studies to analyze data such as pollution levels and population growth rates.
- Home Improvement: DIY projects often require calculations involving square roots for measurements and material estimations.
Common Mistakes and Misconceptions
While working with square roots, several common mistakes and misconceptions can arise. Here’s a detailed look at some of them:
- Forgetting the ± Sign: When solving equations involving square roots, remember to consider both the positive and negative roots unless otherwise specified.
- Incorrect Simplifications: Simplifying expressions like \( \sqrt{a^2} \) as \( a \) without considering the absolute value can lead to errors, as \( \sqrt{a^2} = |a| \).
- Confusion with \( \sqrt{ab} \): Incorrectly assuming \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \) holds for negative numbers or complex numbers can lead to mistakes due to the domain restrictions.
- Misinterpreting Domain: Forgetting that the square root function is only defined for non-negative numbers can lead to erroneous solutions.
- Applying Properties Incorrectly: Incorrectly applying properties such as \( \sqrt{a^2 + b^2} \neq a + b \) without recognizing it as the distance formula derived from the Pythagorean theorem.
- Confusing Square Root with Exponent: Misunderstanding that \( \sqrt{a^2} = a \) only applies when \( a \geq 0 \); for negative \( a \), it is \( \sqrt{a^2} = |a| \).
- Overlooking Restrictions: Failing to account for domain restrictions when simplifying or solving equations involving square roots, which can lead to invalid solutions.
- Skipping Verification: Not verifying solutions obtained from equations involving square roots against the original equation to ensure they are correct and valid.
Advanced Topics in Square Roots
Exploring advanced topics in square roots provides deeper insights into their applications and mathematical properties. Here’s an overview:
- Complex Square Roots: Understanding square roots of negative numbers and their representation using imaginary numbers, such as \( \sqrt{-1} = i \).
- Higher Order Roots: Exploring roots beyond square roots, such as cube roots \( \sqrt[3]{x} \) and higher, involving more complex algebraic manipulations.
- Radicals and Exponents: Delving into radical expressions involving fractional exponents and their relationships with powers and roots.
- Equations with Radical Expressions: Solving equations where variables are under radicals or involve higher order roots, requiring careful manipulation and consideration of domains.
- Geometry and Square Roots: Advanced geometric applications involving square roots, such as the derivation of geometric means and applications in trigonometry.
- Matrices and Determinants: Applications of square roots in linear algebra, particularly in the context of matrices, eigenvalues, and determinants.
- Complex Functions and Analytic Geometry: Analyzing functions involving square roots in complex planes and their implications in analytic geometry.
- History and Development: Tracing the historical development of square root concepts from ancient civilizations to modern mathematical theories and applications.
- Numerical Methods: Algorithms and computational methods for approximating square roots, including iterative methods and their convergence properties.
- Applications in Physics and Engineering: Advanced applications in fields like mechanics, quantum physics, and signal processing, where square roots are fundamental in modeling physical phenomena.

Historical Background of Square Roots
The concept of square roots has a rich historical background dating back to ancient civilizations. Here’s a detailed look at its historical development:
- Ancient Mesopotamia: Babylonian mathematicians around 2000 BC used clay tablets to perform calculations involving square roots.
- Ancient Egypt: Egyptian scribes around 1650 BC documented methods for solving problems related to square roots, though not in the abstract algebraic sense.
- Ancient Greece: Greek mathematicians, including Pythagoras and Euclid, formalized geometric concepts related to squares and square roots, laying the foundation for later developments.
- Indian Mathematics: Scholars in ancient India, particularly during the Vedic period and later in the Gupta Empire (300 BC - 500 AD), developed sophisticated methods for calculating square roots using iterative algorithms.
- Islamic Mathematics: Scholars during the Islamic Golden Age, such as Al-Khwarizmi and Omar Khayyam, made significant contributions to algebra, including the systematic treatment of square roots as part of solving quadratic equations.
- Renaissance Europe: During the Renaissance, European mathematicians like Fibonacci and Cardano further refined algebraic methods for calculating square roots and understanding their properties.
- Modern Mathematics: In the 17th and 18th centuries, mathematicians like Descartes, Newton, and Leibniz incorporated square roots into calculus and the development of analytical geometry, expanding their application in various branches of mathematics and science.
- Contemporary Era: Square roots continue to be fundamental in modern mathematics, with applications ranging from pure mathematics to physics, engineering, computer science, and beyond.
Famous Mathematicians and Their Contributions
Throughout history, numerous mathematicians have made significant contributions to the field of mathematics. Below are some of the most notable mathematicians and their key contributions:
-
Pythagoras (c. 570 – c. 495 BC)
Pythagoras is best known for the Pythagorean theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides: \( a^2 + b^2 = c^2 \).
-
Euclid (c. 300 BC)
Often referred to as the "Father of Geometry," Euclid wrote "Elements," a comprehensive compilation of the knowledge of geometry of his time. This work laid the foundation for modern geometry.
-
Archimedes (c. 287 – c. 212 BC)
Archimedes made significant contributions to geometry, calculus, and mechanics. He is famous for the Archimedean principle, which explains buoyancy, and his method of exhaustion, a precursor to integral calculus.
-
Isaac Newton (1643 – 1727)
Newton co-developed calculus and made groundbreaking contributions to physics, including the laws of motion and universal gravitation. His work "Mathematical Principles of Natural Philosophy" remains a cornerstone in physics.
-
Carl Friedrich Gauss (1777 – 1855)
Known as the "Prince of Mathematicians," Gauss made profound contributions to number theory, statistics, and many other fields. His work on the fundamental theorem of algebra and Gaussian distribution are particularly noteworthy.
-
Leonhard Euler (1707 – 1783)
Euler made significant contributions across various fields, including introducing modern mathematical notation such as \( f(x) \), and working extensively on functions, calculus, and graph theory. Euler's formula \( e^{i\pi} + 1 = 0 \) is famous in complex analysis.
-
Srinivasa Ramanujan (1887 – 1920)
Ramanujan made substantial contributions to mathematical analysis, number theory, infinite series, and continued fractions. Despite having no formal training in pure mathematics, he produced nearly 3900 results, many of which were groundbreaking.
-
Emmy Noether (1882 – 1935)
Noether's theorem, which explains the connection between symmetries and conservation laws in physics, is a cornerstone in theoretical physics. She also made significant contributions to abstract algebra and theoretical physics.
-
Alan Turing (1912 – 1954)
Turing is considered the father of computer science. His work on the Turing machine laid the foundation for modern computing, and he played a crucial role in breaking the Enigma code during World War II.
Video 'Căn Bậc Hai Là Gì?' của thầy J giải thích khái niệm căn bậc hai và cách tính toán đơn giản để giúp học sinh nắm vững kiến thức.
Căn Bậc Hai Là Gì? | Toán Học Với Thầy J
READ MORE:
Video 'CĂN BẬC HAI' giải thích căn bậc hai là gì và giúp trẻ em hiểu khái niệm này qua các bài học thú vị và dễ hiểu.
CĂN BẬC HAI 🚀 Căn Bậc Hai Là Gì? 👨🏻🚀 Toán Học Cho Trẻ Em