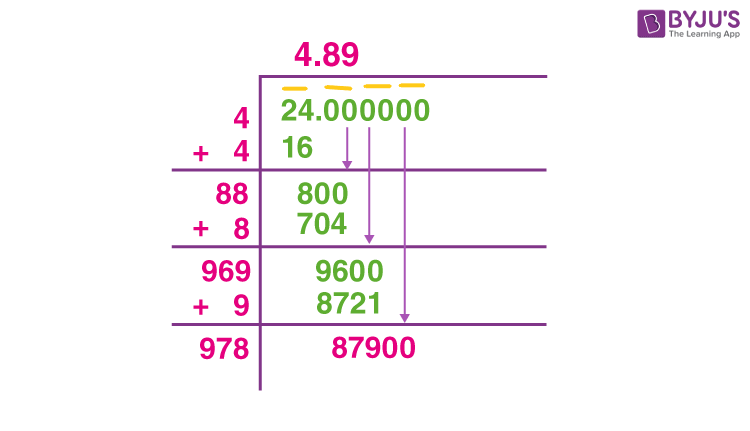
Topic square root property calculator: Discover the power of the Square Root Property Calculator, a versatile tool designed to simplify and solve quadratic equations. Whether you're a student tackling algebra or a professional needing quick calculations, this article will guide you through its features, uses, and benefits.
Table of Content
- Square Root Property Calculator
- Introduction to Square Root Property
- How to Use the Square Root Property Calculator
- Benefits of Using a Square Root Property Calculator
- Mathematical Principles Behind the Square Root Property
- Step-by-Step Guide to Simplifying Square Roots
- Examples of Simplifying Square Roots
- Understanding Perfect Squares
- Properties of Square Roots
- Solving Quadratic Equations Using Square Root Property
- Applications in Algebra
- Square Root Calculation for Fractions
- Online Tools and Resources for Square Root Calculations
- YOUTUBE: Video hướng dẫn cách xấp xỉ căn bậc hai của một số. Học cách tính toán căn bậc hai một cách dễ dàng và nhanh chóng.
Square Root Property Calculator
A square root property calculator is a useful tool for solving quadratic equations using the square root property. This method is particularly effective when dealing with equations that can be simplified to the form \(x^2 = c\), where \(c\) is a constant. The solutions are then found by taking the square root of both sides of the equation.
How It Works
- Isolate the quadratic term: Move all other terms to the opposite side of the equation.
- Take the square root of both sides: Apply the square root to both sides of the equation, remembering to consider both the positive and negative roots.
- Solve for the variable: Simplify the resulting equations to find the solutions for the variable.
Example
Consider the equation \(x^2 = 25\). Using the square root property, we can solve this as follows:
- Isolate the quadratic term: \(x^2 = 25\).
- Take the square root of both sides: \(\sqrt{x^2} = \pm\sqrt{25}\).
- Simplify: \(x = \pm 5\).
Thus, the solutions are \(x = 5\) and \(x = -5\).
Features
- Calculates both positive and negative roots.
- Supports fractional and decimal inputs.
- Provides step-by-step solutions.
- Graphs the equation on the Cartesian plane.
Applications
The square root property calculator is widely used in various fields such as:
- Mathematics: Solving quadratic equations and simplifying expressions.
- Physics: Calculating distances and physical properties involving quadratic relationships.
- Engineering: Analyzing stress and strain in materials.
- Statistics: Determining standard deviations and variances.
Using the Calculator
To use the square root property calculator:
- Enter the quadratic equation in the form \(x^2 = c\).
- Press the "Solve" button.
- View the step-by-step solution and graph, if available.
Mathematical Background
The square root property is based on the principle that every nonnegative real number \(a\) has a unique nonnegative square root, denoted by \(\sqrt{a}\). This property is crucial for solving quadratic equations of the form \(x^2 = c\).
Commonly Used Formulas
| Expression | Result |
|---|---|
| \(\sqrt{x^2}\) | \(|x|\) |
| \(\sqrt{a \times b}\) | \(\sqrt{a} \times \sqrt{b}\) |
| \(\sqrt{\frac{a}{b}}\) | \(\frac{\sqrt{a}}{\sqrt{b}}\) |
Advantages of Using an Online Calculator
- Instant and accurate results.
- Eliminates manual calculation errors.
- Accessible from anywhere with an internet connection.
- Helpful for students and professionals alike.
Conclusion
The square root property calculator is an invaluable tool for solving quadratic equations efficiently and accurately. Whether you are a student, educator, or professional, understanding and utilizing this calculator can greatly enhance your problem-solving skills in various mathematical and scientific contexts.

READ MORE:
Introduction to Square Root Property
The square root property is a fundamental concept in algebra that allows us to solve equations involving squared terms. It states that if \( a^2 = b \), then \( a = \pm\sqrt{b} \). This property is essential for solving quadratic equations, simplifying expressions, and understanding the behavior of various mathematical functions.
The square root property can be expressed mathematically as:
\[
\text{If } x^2 = k, \text{ then } x = \pm\sqrt{k}
\]
Where \( k \) is a non-negative real number. This principle relies on the fact that squaring a number and then taking the square root will return the original number, but it also accounts for both the positive and negative roots.
Here are some key points to understand about the square root property:
- Non-negative Requirement: The number under the square root, \( k \), must be non-negative because the square root of a negative number is not a real number.
- Two Solutions: For any non-zero \( k \), there are always two solutions: \( \sqrt{k} \) and \( -\sqrt{k} \).
- Zero Case: If \( k = 0 \), then the only solution is \( x = 0 \).
- Simplification: The property helps in simplifying expressions and solving quadratic equations efficiently.
Let's consider an example to illustrate the square root property:
Example:
\[
\begin{align*}
x^2 &= 25 \\
x &= \pm\sqrt{25} \\
x &= \pm5
\end{align*}
\]
Therefore, the solutions to the equation \( x^2 = 25 \) are \( x = 5 \) and \( x = -5 \).
The square root property is widely used in various fields of mathematics, including algebra, geometry, and calculus. It also forms the basis for more advanced topics such as complex numbers and differential equations.
Understanding and applying the square root property is crucial for students and professionals dealing with mathematical problems and calculations. By mastering this property, one can solve a variety of equations and simplify complex expressions with confidence and accuracy.
How to Use the Square Root Property Calculator
A square root property calculator is a useful tool designed to simplify the process of solving equations involving square roots. Here's a detailed, step-by-step guide on how to use such a calculator effectively:
-
Input the Equation: Begin by entering the equation you wish to solve into the calculator. The equation should be in the form \( x^2 = k \), where \( k \) is a constant. Ensure that the equation is properly formatted for accurate results.
-
Select the Solve Option: Once the equation is inputted, select the option to solve for \( x \). The calculator will automatically apply the square root property to determine the solutions.
-
View the Results: The calculator will display the solutions for \( x \). According to the square root property, the solutions will be \( x = \pm\sqrt{k} \). For example, if the input equation is \( x^2 = 25 \), the results will be \( x = 5 \) and \( x = -5 \).
-
Interpret the Solutions: Interpret the results provided by the calculator. Remember that the solutions represent the positive and negative square roots of the constant \( k \). This is important for understanding the complete set of solutions to the equation.
-
Check for Extraneous Solutions: Verify the solutions by substituting them back into the original equation. This step ensures that the solutions are correct and that no extraneous solutions were introduced during the calculation.
-
Use Additional Features: Many square root property calculators offer additional features such as graphing, detailed solution steps, and the ability to handle more complex equations. Explore these features to enhance your understanding and problem-solving skills.
By following these steps, you can effectively use a square root property calculator to solve equations and gain a deeper understanding of the mathematical principles involved. This tool simplifies the process and provides accurate solutions, making it an invaluable resource for students, educators, and professionals alike.
Benefits of Using a Square Root Property Calculator
A Square Root Property Calculator offers numerous advantages for students, educators, and anyone dealing with quadratic equations. Here are some key benefits:
- Time Efficiency: Calculating square roots manually can be time-consuming and prone to errors. A calculator provides quick and accurate results, saving valuable time.
- Accuracy: These calculators minimize the risk of human error, ensuring precise solutions to complex equations involving square roots.
- Ease of Use: With a user-friendly interface, square root property calculators are accessible to users of all skill levels, making the process straightforward and understandable.
- Step-by-Step Solutions: Many calculators not only provide the answer but also show the steps involved in reaching the solution, which is educational and helpful for learning purposes.
- Graphical Representation: Some advanced calculators offer graphical solutions, helping users visualize the roots and better understand the behavior of quadratic equations on a Cartesian plane.
- Versatility: These tools are not limited to simple calculations; they can handle a variety of equations, including those with fractions and complex numbers.
- Accessibility: Online calculators can be accessed from any device with an internet connection, making them a convenient resource for on-the-go calculations.
- Free Resources: Many square root property calculators are available for free, making them an economical choice for students and educators.
Using a Square Root Property Calculator can significantly enhance one's understanding and efficiency in solving quadratic equations, making it an invaluable tool in both academic and professional settings.
Mathematical Principles Behind the Square Root Property
The square root property is a fundamental mathematical principle used to solve equations that involve squared terms. This property is especially useful in solving quadratic equations. Here's a detailed look at the mathematical principles behind this property:
-
Definition:
The square root property states that if \( x^2 = m \), where \( m \) is a non-negative real number, then the solutions for \( x \) are given by \( x = \sqrt{m} \) and \( x = -\sqrt{m} \).
Formally, if \( x^2 = m \), then:
\[
x = \pm\sqrt{m}
\] -
Perfect Squares:
A perfect square is an integer that is the square of another integer. For example, \( 1, 4, 9, 16, \) and \( 25 \) are perfect squares because they can be expressed as \( 1^2, 2^2, 3^2, 4^2, \) and \( 5^2 \) respectively. In equations, perfect squares often appear as \( x^2 \) terms.
-
Application to Quadratic Equations:
The square root property is particularly useful in solving quadratic equations of the form \( ax^2 + c = 0 \). By isolating the \( x^2 \) term, we can apply the square root property to find the solutions.
For example, consider the equation:
\[
3x^2 - 12 = 0
\]First, isolate the \( x^2 \) term:
\[
3x^2 = 12
\]Then, divide both sides by 3:
\[
x^2 = 4
\]Finally, apply the square root property:
\[
x = \pm\sqrt{4}
\]Thus, the solutions are \( x = 2 \) and \( x = -2 \).
-
Properties of Roots:
-
Multiplicative Property:
The square root of a product is equal to the product of the square roots of the factors. For any non-negative numbers \( a \) and \( b \), this can be expressed as:
\[
\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}
\] -
Quotient Property:
The square root of a quotient is equal to the quotient of the square roots. For any non-negative numbers \( a \) and \( b \) (with \( b \neq 0 \)), this can be expressed as:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\] -
Equality Property:
If two numbers are equal, their square roots are also equal. For any non-negative numbers \( a \) and \( b \), if \( a = b \), then:
\[
\sqrt{a} = \sqrt{b}
\]
-
Multiplicative Property:
-
Solving Quadratic Equations:
The square root property is a powerful tool for solving quadratic equations that do not have a linear term (i.e., \( b = 0 \)). By isolating the squared term and taking the square root of both sides, we can easily find the solutions to these equations.
For example, to solve \( x^2 - 9 = 0 \), we isolate the \( x^2 \) term:
\[
x^2 = 9
\]Then apply the square root property:
\[
x = \pm\sqrt{9}
\]Thus, the solutions are \( x = 3 \) and \( x = -3 \).

Step-by-Step Guide to Simplifying Square Roots
Simplifying square roots can seem challenging, but by following a systematic approach, it becomes more manageable. Here is a step-by-step guide to help you simplify square roots:
-
Identify Perfect Squares:
Look for factors of the number under the square root (the radicand) that are perfect squares. Perfect squares are numbers like 1, 4, 9, 16, 25, etc.
-
Factor the Radicand:
Write the radicand as a product of two numbers, where one is the largest perfect square factor.
For example, to simplify \( \sqrt{72} \), note that 36 is a perfect square and a factor of 72:
\[
\sqrt{72} = \sqrt{36 \times 2}
\] -
Apply the Product Property:
Use the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
Using the example above:
\[
\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2}
\] -
Simplify the Square Root:
Simplify the square root of the perfect square factor.
\[
\sqrt{36} = 6
\]So,
\[
\sqrt{72} = 6 \sqrt{2}
\] -
Combine the Results:
Write the simplified form by combining the simplified square root with any remaining factors.
The simplified form of \( \sqrt{72} \) is \( 6\sqrt{2} \).
Let's go through another example to reinforce the steps:
- Example: Simplify \( \sqrt{50} \).
- Identify perfect square factors of 50. Here, 25 is a perfect square and a factor of 50.
-
Write 50 as a product of 25 and 2:
\[
\sqrt{50} = \sqrt{25 \times 2}
\] -
Apply the product property:
\[
\sqrt{50} = \sqrt{25} \times \sqrt{2}
\] -
Simplify the square root of 25:
\[
\sqrt{25} = 5
\]So,
\[
\sqrt{50} = 5 \sqrt{2}
\]
By following these steps, you can simplify any square root expression effectively. Remember to practice with different numbers to become more comfortable with the process.
Examples of Simplifying Square Roots
Simplifying square roots involves expressing a square root in its simplest radical form. Here are a few examples demonstrating different methods for simplifying square roots:
Example 1: Simplifying √50
- Factor the number under the square root into its prime factors: \(50 = 2 \times 5^2\).
- Rewrite the square root using these factors: \(\sqrt{50} = \sqrt{2 \times 5^2}\).
- Separate the square root into individual square roots: \(\sqrt{50} = \sqrt{2} \times \sqrt{5^2}\).
- Simplify the square root of the perfect square: \(\sqrt{5^2} = 5\).
- Combine the results: \(\sqrt{50} = 5\sqrt{2}\).
Example 2: Simplifying √72
- Factor the number under the square root into its prime factors: \(72 = 2^3 \times 3^2\).
- Rewrite the square root using these factors: \(\sqrt{72} = \sqrt{2^3 \times 3^2}\).
- Separate the square root into individual square roots: \(\sqrt{72} = \sqrt{2^3} \times \sqrt{3^2}\).
- Simplify the square root of the perfect square: \(\sqrt{3^2} = 3\).
- Rewrite the remaining square root: \(\sqrt{2^3} = \sqrt{2^2 \times 2} = 2\sqrt{2}\).
- Combine the results: \(\sqrt{72} = 3 \times 2\sqrt{2} = 6\sqrt{2}\).
Example 3: Simplifying √18
- Factor the number under the square root into its prime factors: \(18 = 2 \times 3^2\).
- Rewrite the square root using these factors: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Separate the square root into individual square roots: \(\sqrt{18} = \sqrt{2} \times \sqrt{3^2}\).
- Simplify the square root of the perfect square: \(\sqrt{3^2} = 3\).
- Combine the results: \(\sqrt{18} = 3\sqrt{2}\).
Example 4: Simplifying √8
- Factor the number under the square root into its prime factors: \(8 = 2^3\).
- Rewrite the square root using these factors: \(\sqrt{8} = \sqrt{2^3}\).
- Separate the square root into individual square roots: \(\sqrt{8} = \sqrt{2^2 \times 2}\).
- Simplify the square root of the perfect square: \(\sqrt{2^2} = 2\).
- Combine the results: \(\sqrt{8} = 2\sqrt{2}\).
These examples demonstrate the process of breaking down the number under the square root into its prime factors and simplifying the square root of any perfect squares found within the factors. Practicing these steps will help in mastering the simplification of square roots.
Understanding Perfect Squares
Perfect squares are integers that are the square of another integer. In other words, a number is a perfect square if it can be expressed as the product of an integer with itself. For example, 1, 4, 9, 16, 25, and 36 are all perfect squares because:
- 1 = 1 × 1
- 4 = 2 × 2
- 9 = 3 × 3
- 16 = 4 × 4
- 25 = 5 × 5
- 36 = 6 × 6
Understanding perfect squares is crucial in simplifying square roots, solving quadratic equations, and various other mathematical operations.
Properties of Perfect Squares
- The square root of a perfect square is always an integer.
- Perfect squares are always non-negative.
- The difference between successive perfect squares is an odd number.
- Numbers ending in 2, 3, 7, or 8 are never perfect squares.
Examples of Perfect Squares
Let's look at some examples of perfect squares:
| Number | Square | Square Root |
|---|---|---|
| 1 | 1 | 1 |
| 4 | 16 | 2 |
| 9 | 81 | 3 |
| 16 | 256 | 4 |
| 25 | 625 | 5 |
Importance of Perfect Squares in Algebra
Perfect squares play a significant role in algebra, especially in solving quadratic equations. When an equation can be factored into the form (x-a)² = b, recognizing perfect squares simplifies the solving process. For instance:
Solve the equation (x-3)² = 9:
- Take the square root of both sides: x - 3 = ±3
- Solve for x: x = 3 + 3 or x = 3 - 3
- Thus, x = 6 or x = 0
Perfect squares also help in understanding the geometry of squares and the distribution of area. The area of a square is the side length squared, which directly correlates to the concept of perfect squares.
By mastering perfect squares, one can enhance their mathematical problem-solving skills, making calculations and algebraic manipulations more efficient.
Properties of Square Roots
The properties of square roots are fundamental to understanding how to manipulate and simplify expressions involving square roots. Here are some key properties:
- Product Property: The square root of a product is equal to the product of the square roots of each factor.
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Example: \(\sqrt{36 \cdot 25} = \sqrt{36} \cdot \sqrt{25} = 6 \cdot 5 = 30\)
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator.
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Example: \(\sqrt{\frac{49}{16}} = \frac{\sqrt{49}}{\sqrt{16}} = \frac{7}{4}\)
- Power Property: The square root of a power can be expressed as the base raised to half the exponent.
- \(\sqrt{a^n} = a^{\frac{n}{2}}\)
- Example: \(\sqrt{16^2} = 16^{\frac{2}{2}} = 16^1 = 16\)
- Non-negative Property: The square root of any non-negative number is also non-negative.
- \(\sqrt{a} \geq 0 \text{ for } a \geq 0\)
- Example: \(\sqrt{9} = 3\), \(\sqrt{0} = 0\)
- Addition and Subtraction: Square roots cannot be added or subtracted unless they have the same radicand (the number under the square root).
- \(\sqrt{a} + \sqrt{b} \neq \sqrt{a+b}\)
- Example: \(\sqrt{4} + \sqrt{9} \neq \sqrt{13}\) (since \(\sqrt{4} + \sqrt{9} = 2 + 3 = 5\))
- Simplification: Simplifying square roots involves factoring out perfect squares from under the root.
- Example: \(\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}\)
These properties are crucial for solving equations, simplifying expressions, and understanding the behavior of functions involving square roots.

Solving Quadratic Equations Using Square Root Property
The square root property is a useful method for solving quadratic equations of the form \( ax^2 + bx + c = 0 \). This technique is particularly effective when the equation can be rearranged to \( x^2 = k \), where \( k \) is a constant. The steps below outline how to solve quadratic equations using the square root property:
- Isolate the Quadratic Term:
First, rearrange the equation so that the quadratic term is isolated on one side of the equation. For example, given the equation \( x^2 - 16 = 0 \), isolate \( x^2 \) by adding 16 to both sides:
\( x^2 = 16 \)
- Apply the Square Root Property:
Take the square root of both sides of the equation. Remember to consider both the positive and negative square roots. For \( x^2 = 16 \):
\( x = \pm \sqrt{16} \)
\( x = \pm 4 \)
- Solve for the Variable:
Write down the solutions obtained from taking the square root. For the example above, the solutions are:
\( x = 4 \) and \( x = -4 \)
- Check the Solutions:
Substitute the solutions back into the original equation to verify their correctness. For \( x = 4 \) and \( x = -4 \) in \( x^2 - 16 = 0 \):
\( 4^2 - 16 = 0 \)
\( 16 - 16 = 0 \) (True)
\( (-4)^2 - 16 = 0 \)
\( 16 - 16 = 0 \) (True)
Let's consider another example for clarity:
- Example: Solve \( x^2 - 9 = 0 \).
- Isolate the quadratic term: \( x^2 = 9 \).
- Apply the square root property: \( x = \pm \sqrt{9} \).
- Solve for the variable: \( x = 3 \) and \( x = -3 \).
- Check the solutions:
- For \( x = 3 \): \( 3^2 - 9 = 0 \rightarrow 9 - 9 = 0 \) (True).
- For \( x = -3 \): \( (-3)^2 - 9 = 0 \rightarrow 9 - 9 = 0 \) (True).
By following these steps, you can effectively use the square root property to solve quadratic equations. This method simplifies the process and provides a straightforward approach to finding the roots of the equation.
Applications in Algebra
The square root property is a fundamental tool in algebra, particularly useful in solving quadratic equations. It provides a method for finding the roots of an equation of the form x^2 = k by applying the principle that if x^2 = k, then x = ±√k.
Here are some specific applications of the square root property in algebra:
-
Solving Quadratic Equations:
To solve an equation like
x^2 = a, you can take the square root of both sides. This gives two solutions:- If
x^2 = 25, thenx = ±√25, which simplifies tox = ±5. - If
x^2 = 20, thenx = ±√20, which simplifies tox = ±2√5.
- If
-
Solving Quadratic Equations with Complex Terms:
For equations of the form
(x - h)^2 = k, isolate the quadratic term and then apply the square root property. For example:- If
(x + 3)^2 = 49, take the square root of both sides to getx + 3 = ±7, then solve forxto getx = 4orx = -10.
- If
-
Applications in Geometry:
The square root property is used in geometric problems involving areas and distances. For instance, if you know the area of a square, you can find the side length by taking the square root of the area.
- If the area of a square is 36 square units, the side length is
√36 = 6units.
- If the area of a square is 36 square units, the side length is
-
Quadratic Form Equations:
Some equations can be rewritten in a quadratic form, such as
ax^2 + bx + c = 0, which can be solved using the square root property after completing the square.- For example, solve
2x^2 + 8 = 0by first isolating the quadratic term:2x^2 = -8, thenx^2 = -4. Since there is no real number solution for the square root of a negative number, this indicates complex solutions.
- For example, solve
-
Solving Equations with Rational Expressions:
The square root property also applies to equations involving fractions. To solve these, first clear the fraction and then apply the square root property.
- For example, to solve
(3x/2)^2 = 25, first clear the fraction by multiplying both sides by 4:9x^2 = 100, then apply the square root property:3x = ±10, solving forxgivesx = ±10/3.
- For example, to solve
The square root property is a versatile and powerful method in algebra, making it easier to handle various types of equations. Its applications extend beyond simple quadratic equations to more complex algebraic structures, enhancing problem-solving techniques in mathematics.
Square Root Calculation for Fractions
The square root of a fraction can be calculated by separately finding the square root of the numerator and the denominator. This process simplifies the computation and ensures accurate results. Here's a step-by-step guide:
- Identify the fraction: Ensure the fraction is in the form x/y, where x is the numerator and y is the denominator.
- Find the square root of the numerator: Calculate the square root of x. Represent this as √x.
- Find the square root of the denominator: Calculate the square root of y. Represent this as √y.
- Combine the results: The square root of the fraction x/y is √x/√y, which simplifies to √(x/y).
- Simplify the result: If possible, simplify the resulting fraction.
For instance, let's consider the fraction 4/16:
- The numerator is 4, and the denominator is 16.
- Calculate the square root of 4: √4 = 2.
- Calculate the square root of 16: √16 = 4.
- Combine the results: √(4/16) = 2/4.
- Simplify the fraction: 2/4 = 1/2.
Therefore, the square root of 4/16 is 1/2.
Here are some additional examples:
- √(20/29) = √20 / √29 ≈ 0.83
- √(16/49) = √16 / √49 = 4/7 ≈ 0.57
- √(81/24) = √81 / √24 ≈ 1.84
By following these steps, you can accurately find the square root of any fraction.
Online Tools and Resources for Square Root Calculations
Utilizing online tools and resources can significantly simplify the process of calculating square roots. Here are some of the best tools available:
-
Mathway:
Mathway offers a comprehensive square root calculator that allows users to enter a radical expression and get the square root in exact and decimal form. It's particularly useful for algebra students and can be accessed .
-
Good Calculators:
Good Calculators provides a user-friendly square root calculator that reduces any square root to its simplest radical form. The tool is available and also offers other mathematical calculators.
-
Calculator.iO:
Calculator.iO features a square root calculator that returns both the principal and negative square roots of a number. It indicates whether the input is a perfect square and can be found .
-
Omni Calculator:
Omni Calculator is another excellent tool that not only calculates square roots but also simplifies them step-by-step. You can access it .
-
MathWarehouse:
MathWarehouse offers a versatile square root calculator that handles both real and imaginary square roots, reducing them to their simplest forms. Explore this tool .
These tools are invaluable for students, educators, and anyone needing quick and accurate square root calculations. Many of these calculators provide step-by-step solutions, which can help users understand the underlying mathematical principles.

Video hướng dẫn cách xấp xỉ căn bậc hai của một số. Học cách tính toán căn bậc hai một cách dễ dàng và nhanh chóng.
Cách Xấp Xỉ Căn Bậc Hai Của Một Số
READ MORE:
Video giải thích về tính chất căn bậc hai và cách áp dụng chúng trong các bài toán.
Tính Chất Căn Bậc Hai