Topic square root definition math: The concept of the square root is fundamental in mathematics, offering a gateway to various applications in algebra, geometry, physics, and more. This article explores the definition, properties, and significance of square roots, providing clear examples and practical insights to deepen your understanding of this essential mathematical operation.
Table of Content
- Square Root Definition in Mathematics
- Introduction to Square Roots
- Mathematical Definition and Notation
- Examples of Square Roots
- Calculating Square Roots
- Square Roots of Positive Numbers
- Square Roots of Zero
- Square Roots of Negative Numbers
- Square Roots in Complex Numbers
- Square Roots in Geometry
- Square Roots in Algebra
- Square Roots in Physics
- Square Roots in Statistics
- Historical Context of Square Roots
- Common Misconceptions about Square Roots
- Advanced Topics on Square Roots
- Conclusion
- YOUTUBE: Khám phá khái niệm căn bậc hai qua video này với Thầy J. Được giải thích một cách dễ hiểu và thu hút, giúp bạn nắm vững kiến thức toán học cơ bản.
Square Root Definition in Mathematics
In mathematics, the square root of a number is a value that, when multiplied by itself, gives the original number. The square root of a number x is denoted as \(\sqrt{x}\).
Mathematical Representation
The square root of a number x can be represented mathematically as:
\[ \sqrt{x} = y \iff y^2 = x \]
Here, \(y\) is the square root of \(x\).
Properties of Square Roots
- For any non-negative number x, \(\sqrt{x}\) is always non-negative.
- The square root of 0 is 0: \(\sqrt{0} = 0\).
- The square root of 1 is 1: \(\sqrt{1} = 1\).
- \(\sqrt{x^2} = |x|\), where \(|x|\) denotes the absolute value of x.
- Square root function is the inverse of the square function: \( \sqrt{(y^2)} = |y| \).
Examples
Here are a few examples of square roots:
- \(\sqrt{4} = 2\) because \(2^2 = 4\).
- \(\sqrt{9} = 3\) because \(3^2 = 9\).
- \(\sqrt{16} = 4\) because \(4^2 = 16\).
- \(\sqrt{25} = 5\) because \(5^2 = 25\).
Square Root of Negative Numbers
In the context of real numbers, the square root of a negative number is not defined. However, in the context of complex numbers, the square root of a negative number can be defined using the imaginary unit \(i\), where \(i = \sqrt{-1}\). For example:
\(\sqrt{-4} = 2i\) because \((2i)^2 = -4\).
Applications of Square Roots
- Solving quadratic equations.
- Geometry, for finding the lengths of sides in right triangles (Pythagorean theorem).
- Physics, for calculating distances, speeds, and other quantities.
- Statistics, for standard deviation and variance calculations.

READ MORE:
Introduction to Square Roots
The concept of the square root is a fundamental aspect of mathematics, essential for understanding various mathematical operations and applications. The square root of a number is a value that, when multiplied by itself, results in the original number. It is denoted by the radical symbol \(\sqrt{}\) and has important properties and uses in many fields of mathematics and science.
Mathematically, the square root of a number \(x\) is written as \(\sqrt{x}\) and defined as follows:
\[ \sqrt{x} = y \iff y^2 = x \]
Here, \(y\) is the square root of \(x\), meaning that \(y\) multiplied by itself equals \(x\).
Key properties of square roots include:
- Non-negative Result: For any non-negative number \(x\), \(\sqrt{x}\) is always non-negative.
- Square Root of Zero: The square root of 0 is 0: \(\sqrt{0} = 0\).
- Square Root of One: The square root of 1 is 1: \(\sqrt{1} = 1\).
- Absolute Value: \(\sqrt{x^2} = |x|\), where \(|x|\) denotes the absolute value of \(x\).
Examples of square roots help illustrate these properties:
- \(\sqrt{4} = 2\) because \(2^2 = 4\).
- \(\sqrt{9} = 3\) because \(3^2 = 9\).
- \(\sqrt{16} = 4\) because \(4^2 = 16\).
- \(\sqrt{25} = 5\) because \(5^2 = 25\).
In addition to positive numbers, the concept of square roots can be extended to negative numbers using imaginary numbers. The imaginary unit \(i\) is defined as \(\sqrt{-1}\), allowing for the square roots of negative numbers to be expressed. For example:
\(\sqrt{-4} = 2i\) because \((2i)^2 = -4\).
Understanding square roots is crucial for solving equations, particularly quadratic equations, and for various applications in geometry, such as determining the lengths of sides in right triangles through the Pythagorean theorem. Additionally, square roots are used in physics to calculate distances and speeds, and in statistics to compute standard deviation and variance.
Mathematical Definition and Notation
The square root of a number is a mathematical operation that identifies a value which, when multiplied by itself, equals the original number. The square root is represented by the radical symbol \(\sqrt{}\). For a given number \(x\), the square root is written as \(\sqrt{x}\).
Formally, the square root of a number \(x\) is defined as follows:
\[ \sqrt{x} = y \iff y^2 = x \]
In this equation, \(y\) is the square root of \(x\), indicating that \(y\) multiplied by itself results in \(x\). This can be expressed in a step-by-step manner:
- Identify the original number \(x\).
- Find a number \(y\) such that \(y \times y = x\).
- Write \(y\) as \(\sqrt{x}\).
The square root function has several important properties:
- Non-Negative Result: For any non-negative number \(x\), the square root \(\sqrt{x}\) is also non-negative.
- Zero Property: The square root of zero is zero: \(\sqrt{0} = 0\).
- Identity Property: The square root of one is one: \(\sqrt{1} = 1\).
- Absolute Value: For any real number \(x\), \(\sqrt{x^2} = |x|\), where \(|x|\) denotes the absolute value of \(x\).
Examples to illustrate these properties include:
- \(\sqrt{4} = 2\) because \(2^2 = 4\).
- \(\sqrt{9} = 3\) because \(3^2 = 9\).
- \(\sqrt{16} = 4\) because \(4^2 = 16\).
- \(\sqrt{25} = 5\) because \(5^2 = 25\).
Square roots can also be applied to negative numbers by using imaginary numbers. The imaginary unit \(i\) is defined as \(\sqrt{-1}\), enabling the calculation of square roots of negative numbers. For instance:
\(\sqrt{-4} = 2i\) because \((2i)^2 = -4\).
Understanding the mathematical definition and notation of square roots is essential for solving various mathematical problems and for applications in fields such as algebra, geometry, physics, and statistics.
Examples of Square Roots
Here are some examples of square roots:
- The square root of 4 is \( \sqrt{4} = 2 \).
- The square root of 9 is \( \sqrt{9} = 3 \).
- The square root of 16 is \( \sqrt{16} = 4 \).
- The square root of 25 is \( \sqrt{25} = 5 \).
- The square root of 36 is \( \sqrt{36} = 6 \).
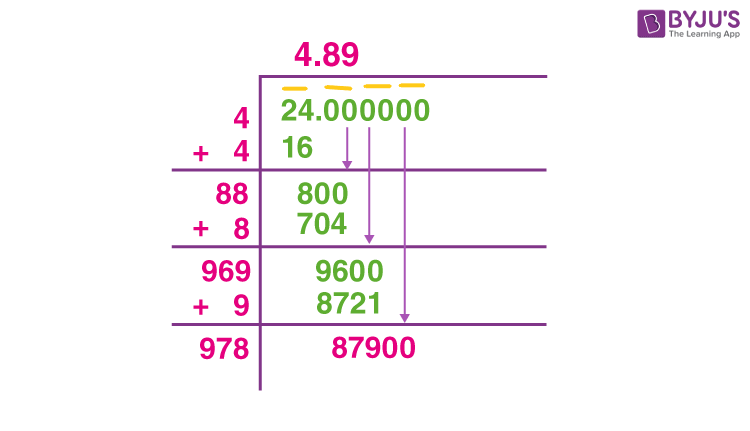
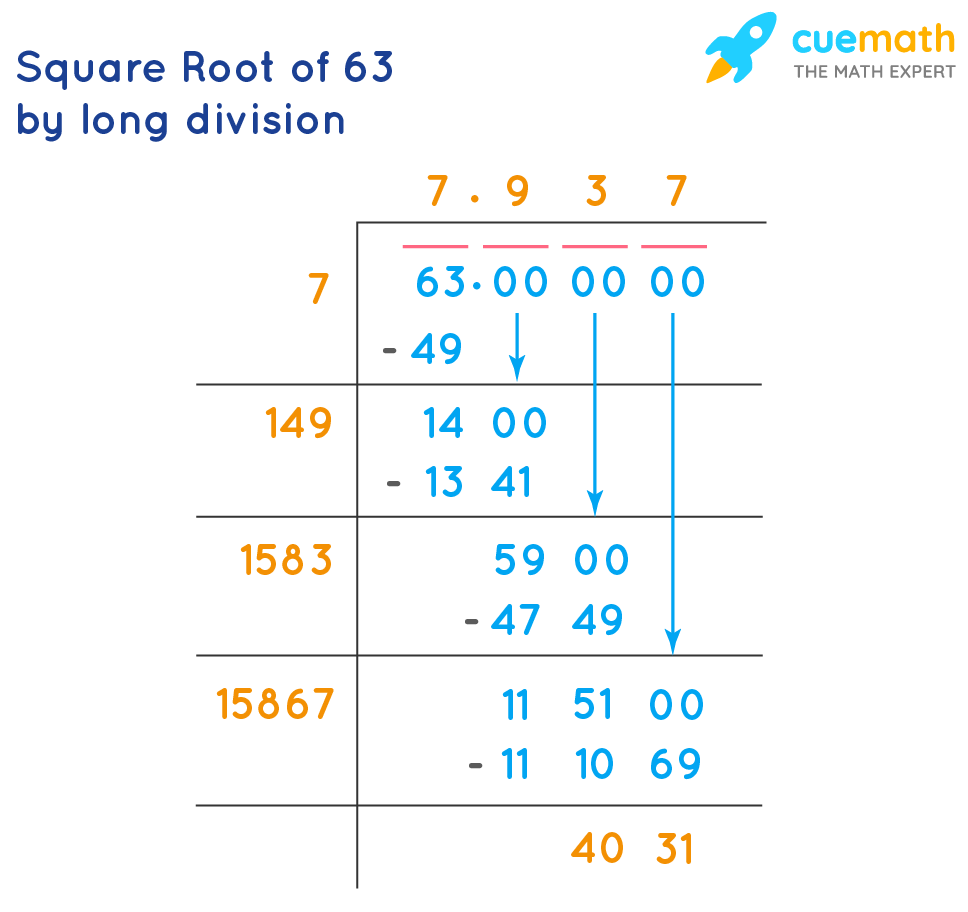
Calculating Square Roots
Here's a step-by-step method for calculating square roots:
- Estimate: Start by estimating the square root. Find the closest perfect square below the number.
- Divide and Average: Divide the number by the estimate. Take the average of the result and the estimate.
- Repeat: Refine your estimate by repeating the division and averaging process until you reach the desired level of accuracy.
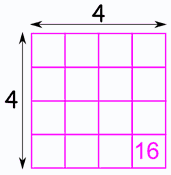
Square Roots of Positive Numbers
For positive real numbers:
- The square root of a positive number \( x \), denoted as \( \sqrt{x} \), is a non-negative number such that \( (\sqrt{x})^2 = x \).
- Examples include \( \sqrt{4} = 2 \), \( \sqrt{9} = 3 \), and \( \sqrt{16} = 4 \).
- Square roots of positive numbers are always positive. For instance, \( \sqrt{25} = 5 \).
Square Roots of Zero
Regarding square roots of zero:
- The principal square root of 0 is \( \sqrt{0} = 0 \).
- Zero is the only non-negative real number whose square root is itself.
- Mathematically, \( (\sqrt{0})^2 = 0 \).
Square Roots of Negative Numbers
When dealing with square roots of negative numbers:
- In real number arithmetic, the square root of a negative number is not a real number but is defined in the realm of complex numbers.
- The principal square root of -1 is denoted as \( \sqrt{-1} = i \), where \( i \) is the imaginary unit.
- For any negative real number \( x \), \( \sqrt{x} \) is not defined in the set of real numbers, but \( \sqrt{x} = i\sqrt{|x|} \) in the complex number system.
Square Roots in Complex Numbers
When discussing square roots in complex numbers:
- A complex number \( z \) can be expressed in the form \( z = a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit.
- The square root of a complex number \( z = a + bi \) can have two possible values, \( \sqrt{z} = \pm \sqrt{r} \left( \cos\left( \frac{\theta}{2} \right) + i \sin\left( \frac{\theta}{2} \right) \right) \), where \( r = \sqrt{a^2 + b^2} \) and \( \theta = \tan^{-1}\left(\frac{b}{a}\right) \).
- This formula utilizes the polar form of complex numbers to compute square roots.

Square Roots in Geometry
In geometry, square roots are used in various contexts:
- Calculating Side Lengths: Square roots are used to find the lengths of sides of squares and rectangles, given their areas.
- Pythagorean Theorem: The Pythagorean theorem involves square roots to determine the length of the hypotenuse of a right triangle.
- Circle and Radius: In a circle, the radius is related to the area and vice versa using square roots.
- Distance Formula: The distance between two points in a coordinate plane is computed using square roots derived from the Pythagorean theorem.
Square Roots in Algebra
Square roots play a significant role in algebra, particularly in solving equations and simplifying expressions. Understanding how to work with square roots is essential for mastering various algebraic concepts.
Definition and Basic Properties
The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). The square root is denoted by the radical symbol \( \sqrt{} \). For example, \( \sqrt{25} = 5 \) because \( 5^2 = 25 \).
Key properties of square roots include:
- Principal Square Root: The non-negative square root of \( x \), denoted \( \sqrt{x} \), is called the principal square root.
- Negative Square Root: The negative counterpart of the principal square root, denoted \( -\sqrt{x} \).
- Product Property: \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \), valid for non-negative \( a \) and \( b \).
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), valid for non-negative \( a \) and positive \( b \).
Solving Quadratic Equations
Square roots are often used to solve quadratic equations of the form \( x^2 = a \). These equations have two solutions: the principal square root and its negative counterpart.
Example:
Solve \( x^2 = 16 \).
The solutions are \( x = \sqrt{16} \) and \( x = -\sqrt{16} \). Therefore, \( x = 4 \) and \( x = -4 \).
Simplifying Square Roots
Square roots can often be simplified by factoring out perfect squares.
Example:
Simplify \( \sqrt{72} \).
First, factor 72 into its prime factors: \( 72 = 2^3 \cdot 3^2 \). Then, apply the product property:
\[
\sqrt{72} = \sqrt{2^3 \cdot 3^2} = \sqrt{2^2 \cdot 2 \cdot 3^2} = \sqrt{(2 \cdot 3)^2 \cdot 2} = 6\sqrt{2}
\]
Algebraic Applications
Square roots are used in various algebraic applications, including solving quadratic equations, simplifying radical expressions, and working with functions.
Example:
Solve the equation \( 2x^2 - 8 = 0 \).
First, isolate the quadratic term:
\[
2x^2 = 8 \implies x^2 = 4
\]
Then, take the square root of both sides:
\[
x = \pm\sqrt{4} \implies x = \pm2
\]
Graphing Square Root Functions
The square root function \( f(x) = \sqrt{x} \) is a common algebraic function. Its graph is a curve that starts at the origin (0,0) and increases slowly. This function is defined only for non-negative \( x \) because the square root of a negative number is not a real number.
Example:
Graph the function \( f(x) = \sqrt{x} \).
Plot several points where \( x \) is a perfect square (e.g., \( x = 0, 1, 4, 9, 16 \)). The corresponding \( y \)-values will be \( 0, 1, 2, 3, 4 \). Connect these points with a smooth curve starting at the origin.
Understanding and applying these concepts will enhance your ability to work with square roots in algebra and solve a variety of mathematical problems.
Square Roots in Physics
The concept of square roots plays a vital role in various areas of physics, from mechanics to electromagnetism and beyond. Here are some key applications of square roots in physics:
1. Kinematics and Motion
In kinematics, the square root is often used to determine quantities like speed and velocity. For instance, the magnitude of the velocity \( v \) in uniformly accelerated motion can be found using the equation:
\[ v = \sqrt{v_0^2 + 2a s} \]
where \( v_0 \) is the initial velocity, \( a \) is the acceleration, and \( s \) is the displacement.
2. Wave Mechanics
Square roots appear frequently in the study of waves. For example, the speed \( v \) of a wave on a string is given by:
\[ v = \sqrt{\frac{T}{\mu}} \]
where \( T \) is the tension in the string and \( \mu \) is the mass per unit length of the string.
3. Energy and Power
In the context of energy, the square root is used to relate the kinetic energy \( K \) of an object to its velocity \( v \):
\[ K = \frac{1}{2}mv^2 \quad \Rightarrow \quad v = \sqrt{\frac{2K}{m}} \]
where \( m \) is the mass of the object.
4. Electromagnetism
In electromagnetism, the magnitude of the electric field \( E \) due to a point charge is given by Coulomb's law:
\[ E = k_e \frac{Q}{r^2} \quad \Rightarrow \quad r = \sqrt{\frac{k_e Q}{E}} \]
where \( k_e \) is Coulomb's constant, \( Q \) is the charge, and \( r \) is the distance from the charge.
5. Relativity
In the theory of relativity, time dilation is an important concept that involves square roots. The time dilation formula is:
\[ t' = \frac{t}{\sqrt{1 - \frac{v^2}{c^2}}} \]
where \( t' \) is the dilated time, \( t \) is the proper time, \( v \) is the relative velocity, and \( c \) is the speed of light.
6. Quantum Mechanics
In quantum mechanics, the wave function \( \psi \) often involves square roots when normalizing the probability densities. The normalization condition is:
\[ \int_{-\infty}^{\infty} |\psi(x)|^2 \, dx = 1 \]
where the probability density \( |\psi(x)|^2 \) is sometimes expressed with square roots to ensure proper normalization.
Overall, square roots are fundamental to expressing and solving a wide range of physical equations and concepts. Understanding their use helps in the analysis and interpretation of various physical phenomena.
Square Roots in Statistics
Square roots are widely used in statistics, particularly in measures of variability and spread. One of the primary uses of square roots in statistics is in the calculation of the standard deviation, which is a measure of the dispersion of a set of values.
Standard Deviation
The standard deviation is derived from the variance, which measures the average squared deviation of each number from the mean of the data set. The formula for the variance \( \sigma^2 \) of a population is:
\[
\sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2
\]
where \( N \) is the population size, \( x_i \) is each individual value, and \( \mu \) is the population mean.
To find the standard deviation \( \sigma \), take the square root of the variance:
\[
\sigma = \sqrt{\sigma^2}
\]
Sample Variance and Standard Deviation
For a sample rather than a population, the variance \( s^2 \) is calculated slightly differently to account for the smaller sample size:
\[
s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2
\]
where \( n \) is the sample size and \( \bar{x} \) is the sample mean. The standard deviation \( s \) for a sample is then:
\[
s = \sqrt{s^2}
\]
Example Calculation
Consider a sample with the following weights (in lbs): 127, 134, 155, 171, 202. To calculate the sample variance and standard deviation:
- Calculate the sample mean \( \bar{x} \):
\[
\bar{x} = \frac{127 + 134 + 155 + 171 + 202}{5} = 157.8
\] - Calculate the sum of squares (SS):
\[
SS = (127 - 157.8)^2 + (134 - 157.8)^2 + (155 - 157.8)^2 + (171 - 157.8)^2 + (202 - 157.8)^2 = 3650.8
\] - Calculate the sample variance \( s^2 \):
\[
s^2 = \frac{3650.8}{5-1} = 912.7
\] - Calculate the sample standard deviation \( s \):
\[
s = \sqrt{912.7} \approx 30.2
\]
Applications in Hypothesis Testing
In hypothesis testing, the standard deviation is crucial for determining the spread of the sampling distribution. For example, in the calculation of z-scores and t-scores, which standardize different types of data and allow for comparisons across different units of measurement:
\[
z = \frac{(x - \mu)}{\sigma}
\]
Confidence Intervals
Square roots are also used in the computation of confidence intervals. The standard error of the mean, which is the standard deviation of the sampling distribution of the sample mean, is given by:
\[
SE = \frac{s}{\sqrt{n}}
\]
where \( s \) is the sample standard deviation and \( n \) is the sample size. This helps in constructing confidence intervals around the sample mean.

Historical Context of Square Roots
The concept of the square root has a rich history that spans several millennia, with contributions from various cultures and civilizations. Here, we explore the development of the square root concept through different periods and notable mathematicians.
Ancient Civilizations
- Babylonians: Around 1800 BCE, the Babylonians developed an early method for approximating square roots using a form of iterative calculation known as the Babylonian method or Heron's method.
- Egyptians: The Rhind Mathematical Papyrus, dating to around 1650 BCE, contains evidence that ancient Egyptians had techniques for estimating square roots.
Classical Greece
In ancient Greece, mathematicians made significant advancements in understanding square roots:
- Pythagoreans: The Pythagorean school studied properties of numbers and geometry, contributing to the concept of irrational numbers, including irrational square roots.
- Euclid: Euclid's "Elements" provided a systematic treatment of mathematics, including methods for finding square roots geometrically.
Indian Mathematics
Indian mathematicians made notable contributions to the concept of square roots:
- Āryabhaṭa: In the 5th century CE, Āryabhaṭa included algorithms for extracting square roots in his work "Āryabhaṭīya."
- Brahmagupta: In the 7th century CE, Brahmagupta extended methods for calculating square roots and dealing with negative numbers.
Islamic Golden Age
During the Islamic Golden Age, mathematicians preserved and expanded upon earlier works:
- Al-Khwarizmi: Known as the father of algebra, Al-Khwarizmi's works included methods for solving quadratic equations, which inherently involve square roots.
- Omar Khayyam: In the 11th century, Khayyam provided geometric solutions to cubic equations, laying groundwork for further studies involving square roots.
European Renaissance
In the Renaissance, European scholars translated and built upon earlier works:
- Leonardo of Pisa (Fibonacci): In the 13th century, Fibonacci introduced European readers to the Hindu-Arabic numeral system and methods for calculating square roots in his "Liber Abaci."
- René Descartes: In the 17th century, Descartes' development of the Cartesian coordinate system facilitated algebraic solutions involving square roots.
Modern Era
In modern mathematics, the concept of square roots has been rigorously formalized:
- Numerical Methods: Modern numerical methods, including Newton's method, have refined techniques for computing square roots efficiently and accurately.
- Computational Advances: With the advent of computers, algorithms for calculating square roots have become integral to various fields of science and engineering.
The historical development of square roots is a testament to the collective efforts of mathematicians across cultures and eras, illustrating the enduring quest to understand and compute this fundamental mathematical concept.
Common Misconceptions about Square Roots
Understanding square roots is crucial in mathematics, yet several common misconceptions persist among students. Below, we address these misunderstandings and provide clarifications:
-
Misconception: \( \sqrt{a} \times \sqrt{b} = \sqrt{ab} \) always holds true
This identity is only valid when both \(a\) and \(b\) are non-negative. If \(a\) and \(b\) are both negative, the equation does not hold. For instance, \(\sqrt{-1} \times \sqrt{-1} = i \times i = -1\), but \(\sqrt{(-1) \times (-1)} = \sqrt{1} = 1\).
-
Misconception: \( \sqrt{x + y} = \sqrt{x} + \sqrt{y} \)
This is incorrect. The square root of a sum is not equal to the sum of the square roots. For example, \(\sqrt{4 + 9} = \sqrt{13}\), whereas \(\sqrt{4} + \sqrt{9} = 2 + 3 = 5\).
-
Misconception: Negative numbers do not have square roots
In the real number system, negative numbers do not have real square roots. However, in the complex number system, they do. For example, the square root of -4 is \(2i\), where \(i\) is the imaginary unit.
-
Misconception: \( (\sqrt{a})^2 = a \) for all values of \(a\)
This is true for non-negative values of \(a\). For negative \(a\), \((\sqrt{a})^2\) would involve imaginary numbers, which are not always intuitive.
-
Misconception: Squaring both sides of an equation is always valid
While squaring both sides of an equation can be a useful technique, it must be done carefully because it can introduce extraneous solutions. For example, \(x = -2\) becomes \(x^2 = 4\), which also includes \(x = 2\) as a solution.
By understanding these common misconceptions, students can develop a more accurate and comprehensive grasp of square roots, enhancing their overall mathematical proficiency.
Advanced Topics on Square Roots
Square roots play a crucial role in various advanced mathematical concepts and applications. In this section, we will explore several advanced topics related to square roots, including their properties, algorithms for calculation, and their use in higher mathematics.
Properties of Square Roots
- Rational and Irrational Roots: The square root of a perfect square is a rational number, while the square root of a non-perfect square is irrational.
- Product and Quotient Rules: For any non-negative numbers \(a\) and \(b\), \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \quad \text{and} \quad \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}. \]
Algorithms for Calculating Square Roots
Several algorithms can be used to compute square roots, each with its own applications and efficiency:
- Newton's Method: Also known as the Heron method, it is an iterative numerical method used to approximate square roots. Starting with an initial guess \(x_0\), the formula \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{a}{x_n} \right) \] is used repeatedly to get closer to the actual square root of \(a\).
- Continued Fractions: Square roots of non-square integers can be represented as periodic continued fractions, which provide an efficient way to approximate them.
- Binary Search Method: This method involves narrowing down the interval in which the square root lies by repeatedly dividing the interval in half.
Square Roots in Higher Mathematics
Square roots are fundamental in various branches of higher mathematics, including:
- Complex Numbers: The square root of a negative number is defined in terms of complex numbers. For instance, \(\sqrt{-1}\) is denoted as \(i\), the imaginary unit.
- Eigenvalues and Eigenvectors: In linear algebra, the square root of a matrix involves finding a matrix \(B\) such that \(B^2 = A\). This concept is important in the study of matrix functions.
- Quadratic Forms: In advanced algebra, quadratic forms and their properties are analyzed using square roots, particularly when diagonalizing matrices.
Applications in Other Fields
Beyond pure mathematics, square roots are extensively used in various applied fields:
- Physics: In physics, square roots appear in equations describing wave speeds, quantum mechanics, and general relativity. For example, the period of a pendulum is proportional to the square root of its length.
- Engineering: In engineering, square roots are used in signal processing, control theory, and electrical circuit analysis.
- Computer Science: Algorithms involving square roots are crucial in graphics rendering, computational geometry, and optimization problems.
Understanding these advanced topics and their applications highlights the profound importance of square roots in both theoretical and applied mathematics.
Conclusion
The study of square roots is fundamental in mathematics, offering insights into various fields such as algebra, geometry, physics, and statistics. Understanding the definition, properties, and applications of square roots helps build a strong mathematical foundation. The square root function not only aids in solving equations and understanding quadratic relationships but also plays a crucial role in more advanced topics such as complex numbers and calculus.
Throughout history, the concept of the square root has evolved, leading to significant advancements in mathematical theory and application. From ancient civilizations to modern-day mathematics, the square root remains an essential element in both theoretical and applied mathematics.
By mastering square roots, students and professionals can enhance their problem-solving skills and mathematical comprehension. Whether in academic settings or practical applications, the knowledge of square roots is invaluable.
As we continue to explore advanced topics and applications, the importance of a solid understanding of square roots becomes increasingly evident. Embracing this knowledge paves the way for further mathematical discoveries and innovations.
In conclusion, square roots are more than just a mathematical concept; they are a gateway to a deeper understanding of the world around us. By appreciating their significance and applications, we can better appreciate the beauty and utility of mathematics in our daily lives and in the broader scope of scientific inquiry.

Khám phá khái niệm căn bậc hai qua video này với Thầy J. Được giải thích một cách dễ hiểu và thu hút, giúp bạn nắm vững kiến thức toán học cơ bản.
Khái Niệm Căn Bậc Hai Là Gì? | Toán Học với Thầy J
READ MORE:
Tìm hiểu về căn bậc hai qua video này từ Khan Academy. Nội dung rõ ràng và dễ hiểu, phù hợp cho học sinh lớp 8 và giúp bạn nắm vững khái niệm toán học cơ bản.
Giới Thiệu Về Căn Bậc Hai | Số Học và Phép Toán | Lớp 8 | Khan Academy