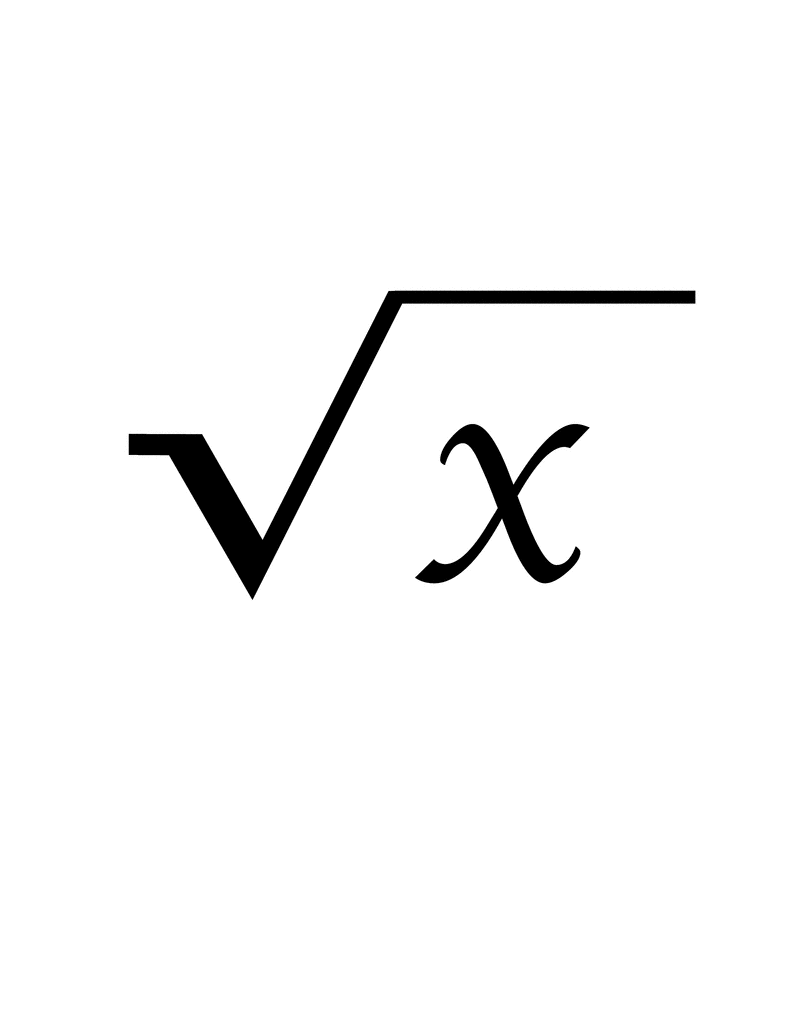Topic square root 1/2: The square root of 1/2 is a fascinating mathematical concept that is both simple and profound. Understanding how to simplify and calculate this value can enhance your grasp of algebra and number theory. In this article, we explore the steps and significance of finding the square root of 1/2 in various mathematical contexts.
Table of Content
- Square Root of 1/2
- Introduction to Square Roots
- Definition and Properties of Square Roots
- Calculating the Square Root of 1/2
- Step-by-Step Simplification
- Mathematical Rules and Rationalization
- Square Root in Decimal Form
- Applications and Examples
- Historical Context and Development
- Square Roots in Different Mathematical Contexts
- Conclusion and Further Reading
- YOUTUBE: Xem video thú vị về câu hỏi: Căn bậc hai của 1/2 có bằng tất cả những con số này không? Tìm câu trả lời và khám phá thêm về căn bậc hai của 1/2.
Square Root of 1/2
The square root of 1/2 can be expressed and simplified in various ways. This involves both exact and decimal forms.
Mathematical Expression
To find the square root of \( \frac{1}{2} \), we can use the property of radicals:
\[ \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} \]
Rationalizing the denominator, we multiply by \( \frac{\sqrt{2}}{\sqrt{2}} \):
\[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
Thus, the simplified form is:
\[ \frac{\sqrt{2}}{2} \]
In decimal form, this is approximately:
\[ \frac{\sqrt{2}}{2} \approx 0.7071 \]
Steps to Simplify
- Rewrite the expression: \(\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}}\)
- Rationalize the denominator: \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
Square and Square Root Relationship
The square root is the inverse operation of squaring a number. For example:
- If \( x^2 = y \), then \( x = \sqrt{y} \).
- If \( y = \frac{1}{2} \), then \( \sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2} \).
Historical Context
The concept of square roots has been studied since ancient times, with significant contributions from various cultures:
- Babylonians approximated square roots using base 60.
- Ancient Greeks identified the irrational nature of square roots for non-perfect squares.
- Indian mathematicians developed methods for finding square roots and their approximations.
| Aspect | Square | Square Root |
|---|---|---|
| Definition | The product of a number multiplied by itself | The number which when multiplied by itself gives the original number |
| Example | 72 = 49 | \(\sqrt{49} = 7\) |
| Symbol | Exponent (^) | Square root (√) |
| Result | Always positive | Can be positive or negative |
| Inverse | Square root | Square |
Understanding these relationships and properties helps in solving equations and various mathematical problems involving square roots.

READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics that represent a value which, when multiplied by itself, gives the original number. The symbol for the square root is √, known as the radical sign. For example, the square root of 9 is 3 because 3 multiplied by itself equals 9.
The square root of a number \( x \) is written as \( \sqrt{x} \). It is important to note that every positive number has two square roots: one positive (principal square root) and one negative. For instance, both 5 and -5 are square roots of 25 because \( 5^2 = 25 \) and \( (-5)^2 = 25 \).
When dealing with fractions under the square root sign, such as \( \frac{1}{2} \), the expression can be simplified by separating the numerator and the denominator:
\[ \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} \]
To rationalize the denominator, multiply both the numerator and the denominator by \( \sqrt{2} \):
\[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \approx 0.707 \]
Understanding the properties of square roots helps in solving quadratic equations and in simplifying radical expressions. For example, solving the equation \( x^2 - 9 = 0 \) involves finding the square roots of 9:
\[ x^2 - 9 = 0 \implies x^2 = 9 \implies x = \pm 3 \]
Square roots also extend to algebraic expressions, such as \( \sqrt{xy} = \sqrt{x} \times \sqrt{y} \), provided \( x \) and \( y \) are non-negative. This property is useful in breaking down more complex expressions into simpler forms.
Definition and Properties of Square Roots
The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). This means that when \( y \) is multiplied by itself, the result is \( x \). The principal square root of \( x \) is denoted as \( \sqrt{x} \) and is always non-negative.
Here are some key properties and rules related to square roots:
- Non-negative Result: The square root of any non-negative number is also non-negative. For example, \( \sqrt{9} = 3 \).
- Principal Square Root: Every non-negative number \( x \) has a unique non-negative square root, known as the principal square root, denoted as \( \sqrt{x} \). For example, the principal square root of 4 is 2.
- Negative Square Roots: While the principal square root is non-negative, every positive number actually has two square roots: one positive and one negative. These can be represented as \( \pm \sqrt{x} \). For instance, the square roots of 16 are \( \pm 4 \).
- Square Root of a Fraction: The square root of a fraction can be found by taking the square root of the numerator and the denominator separately. For example, \( \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \).
- Product Rule: The square root of a product is the product of the square roots: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). For example, \( \sqrt{4 \cdot 9} = \sqrt{36} = 6 \) and \( \sqrt{4} \cdot \sqrt{9} = 2 \cdot 3 = 6 \).
- Quotient Rule: The square root of a quotient is the quotient of the square roots: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{16}{4}} = \sqrt{4} = 2 \) and \( \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2 \).
Square roots have numerous applications in various fields including geometry, physics, and engineering. Understanding these basic properties can help simplify complex mathematical problems and calculations.
Calculating the Square Root of 1/2
The process of calculating the square root of
Initial Expression: Begin with the square root of the fraction
\frac{1}{2} .Apply the Radical Rule: Use the property of radicals to separate the numerator and the denominator:
\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} Simplify the Numerator: The square root of 1 is 1:
\frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} Rationalize the Denominator: To remove the radical from the denominator, multiply the numerator and the denominator by
\sqrt{2} :\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} Final Simplified Form: The simplified form of the square root of
\frac{1}{2} is\frac{\sqrt{2}}{2} , which is approximately 0.7071 in decimal form.
This detailed step-by-step approach helps in understanding the process of calculating and simplifying the square root of a fraction.
Step-by-Step Simplification
The process of simplifying the square root of
-
Rewrite the square root expression using the rule for radicals:
\(\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}}\) -
Simplify the numerator and the denominator:
\(\frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}}\) -
Rationalize the denominator to remove the square root:
Multiply both the numerator and the denominator by
\(\sqrt{2}\) :\(\frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}\) -
Express the final simplified form:
\(\sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2}\) In decimal form, this is approximately
0.7071 .
By following these steps, you can easily simplify the square root of

Mathematical Rules and Rationalization
When dealing with the square root of \( \frac{1}{2} \), mathematical rules and rationalization techniques come into play to simplify and understand its properties:
- Definition: The square root of a number \( x \), denoted as \( \sqrt{x} \), is a value \( y \) such that \( y^2 = x \). For \( \sqrt{\frac{1}{2}} \), this means finding a number \( y \) such that \( y^2 = \frac{1}{2} \).
- Rationalization: To rationalize \( \sqrt{\frac{1}{2}} \), we often multiply the numerator and the denominator by \( \sqrt{2} \) to eliminate the square root in the denominator, resulting in \( \sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2} \).
- Properties:
- The square root of \( \frac{1}{2} \) is an irrational number because \( \sqrt{2} \) is irrational, thus \( \frac{\sqrt{2}}{2} \) is also irrational.
- The decimal representation of \( \sqrt{\frac{1}{2}} \) is approximately 0.70710678.
- Applications: Understanding square roots and rationalization is crucial in various fields such as engineering, physics, and computer science where precise calculations are required.
Square Root in Decimal Form
Exploring the decimal representation of \( \sqrt{\frac{1}{2}} \), we find:
- The exact value of \( \sqrt{\frac{1}{2}} \) in decimal form is approximately 0.70710678.
- This value can be calculated using various computational methods including iterative algorithms or mathematical constants.
- Understanding the decimal form helps in practical applications where precise numerical values are required, such as in measurements and scientific calculations.
Applications and Examples
The square root of \( \frac{1}{2} \) finds practical applications in various fields:
- Engineering: It is used in calculations involving electrical power transmission, where impedance and voltage ratios are crucial.
- Physics: In quantum mechanics, \( \sqrt{\frac{1}{2}} \) appears in the normalization of wavefunctions, ensuring probabilities sum to one.
- Statistics: It plays a role in calculating standard deviations and uncertainties, influencing data analysis and modeling.
- Computer Science: Algorithms for numerical methods, cryptography, and signal processing utilize the square root of \( \frac{1}{2} \) for efficient calculations.
Historical Context and Development
The historical context and development of understanding \( \sqrt{\frac{1}{2}} \) reveal:
- Ancient Roots: Early civilizations approximated square roots geometrically, such as the Babylonians and Egyptians.
- Mathematical Formulation: The concept of irrational numbers, including \( \sqrt{2} \), was developed by Greek mathematicians like Pythagoras and Euclid.
- Renaissance and Modern Era: Advancements in algebra and calculus during the Renaissance and Enlightenment periods refined the understanding of square roots and their applications.
- Symbolic Representation: The adoption of symbols like \( \sqrt{} \) and \( \frac{1}{2} \) in mathematical notation facilitated precise communication and calculation.
- Contemporary Significance: Today, the square root of \( \frac{1}{2} \) continues to be a fundamental concept in mathematics, indispensable in fields ranging from engineering to theoretical physics.
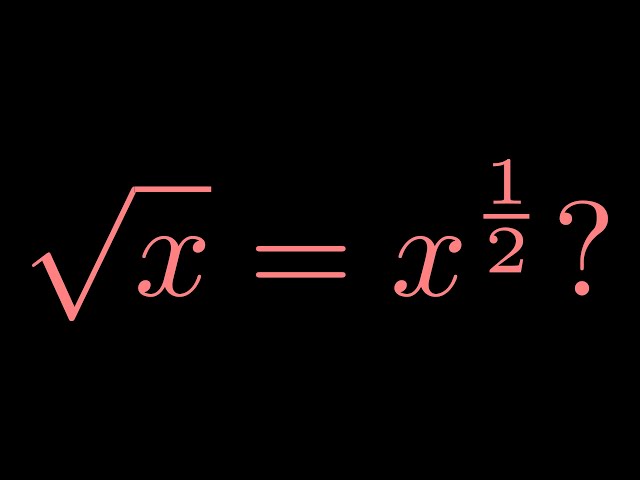
Square Roots in Different Mathematical Contexts
The square root of \( \frac{1}{2} \) manifests in diverse mathematical contexts:
- Geometry: It appears in geometric constructions involving right triangles and the Pythagorean theorem.
- Algebra: Solving quadratic equations often requires considering square roots, including fractions like \( \sqrt{\frac{1}{2}} \).
- Number Theory: The study of irrational numbers, such as \( \sqrt{2} \), is integral to number theory, influencing prime factorization and divisibility.
- Analysis: In calculus, square roots play a role in defining continuous functions and studying limits and derivatives.
- Probability: Statistical distributions involve square roots in calculating standard deviations and probabilities.
Conclusion and Further Reading
In conclusion, exploring \( \sqrt{\frac{1}{2}} \) reveals its significance across various disciplines and historical contexts. Its applications in mathematics, science, and technology underscore its fundamental role in modern society.
Further reading on this topic can delve deeper into:
- Theoretical implications of irrational numbers and their impact on mathematical reasoning.
- Practical applications in fields such as engineering, physics, and computer science.
- Historical developments and the evolution of mathematical notation and concepts related to square roots.
- Advanced mathematical analyses involving square roots and their implications in higher mathematics.
Xem video thú vị về câu hỏi: Căn bậc hai của 1/2 có bằng tất cả những con số này không? Tìm câu trả lời và khám phá thêm về căn bậc hai của 1/2.
Căn bậc hai của 1/2 bằng tất cả các số này! #shorts
READ MORE:
Tại sao 'x mũ một nửa' có nghĩa là căn bậc hai?
Video: Tại sao 'x mũ một nửa' có nghĩa là căn bậc hai?