Topic 9 2 squared: The phrase "9 2 squared" might seem straightforward, but it offers intriguing insights into mathematical principles. Dive into this article to explore how different interpretations can lead to varying results. Whether you're a student, teacher, or math enthusiast, uncover the fascinating world of exponents and multiplication.
Table of Content
- Understanding the Expression \( 9 \times 2^2 \)
- Introduction to "9 2 Squared"
- Understanding Exponents in Mathematics
- Order of Operations: PEMDAS/BODMAS Explained
- Interpreting "9 2 Squared": Multiple Perspectives
- Detailed Calculation for \( 9 \times 2^2 \)
- Detailed Calculation for \( (9 \times 2)^2 \)
- Common Misinterpretations and Clarifications
- Practical Applications of Exponentiation
- Exploring More Complex Mathematical Expressions
- Conclusion: Clear Interpretation in Mathematical Expressions
- YOUTUBE: Video giải thích biểu đồ dư, hệ số tương quan r và r bình phương trong phân tích dữ liệu, giúp bạn hiểu rõ hơn về cách sử dụng chúng trong thống kê.
Understanding the Expression \( 9 \times 2^2 \)
When we come across the expression "9 2 squared", it can be interpreted in different ways. The ambiguity lies in the placement of the parentheses and the order of operations. Let's explore the possibilities and their outcomes.
Possible Interpretations
- Interpretation 1: \( 9 \times 2^2 \)
- Interpretation 2: \( (9 \times 2)^2 \)
Detailed Calculations
-
Calculation for \( 9 \times 2^2 \)
According to the order of operations (PEMDAS/BODMAS), we calculate the exponent first and then multiply:
- Step 1: Calculate \( 2^2 \)
\[ 2^2 = 4 \]
- Step 2: Multiply the result by 9
\[ 9 \times 4 = 36 \]
Thus, \( 9 \times 2^2 = 36 \).
- Step 1: Calculate \( 2^2 \)
-
Calculation for \( (9 \times 2)^2 \)
Here, we first multiply 9 by 2 and then square the result:
- Step 1: Multiply \( 9 \times 2 \)
\[ 9 \times 2 = 18 \]
- Step 2: Square the result
\[ 18^2 = 324 \]
Thus, \( (9 \times 2)^2 = 324 \).
- Step 1: Multiply \( 9 \times 2 \)
Conclusion
The expression "9 2 squared" can lead to different results depending on how it's interpreted:
- Using \( 9 \times 2^2 \), the result is \( 36 \).
- Using \( (9 \times 2)^2 \), the result is \( 324 \).
It's important to clarify the intended interpretation to avoid confusion.
READ MORE:
Introduction to "9 2 Squared"
The expression "9 2 squared" is an interesting mathematical term that often leads to different interpretations. Understanding it requires a solid grasp of mathematical principles, especially the order of operations. Here, we'll explore what "9 2 squared" means and how to solve it step by step.
The phrase can be approached in two primary ways:
- Interpretation 1: Multiplying 9 by the square of 2.
- Interpretation 2: Squaring the product of 9 and 2.
Let's delve into each interpretation:
-
Multiplying 9 by the square of 2:
First, we calculate the square of 2 and then multiply the result by 9.
- Step 1: Compute \( 2^2 \)
\[ 2^2 = 4 \]
- Step 2: Multiply 9 by 4
\[ 9 \times 4 = 36 \]
So, \( 9 \times 2^2 = 36 \).
- Step 1: Compute \( 2^2 \)
-
Squaring the product of 9 and 2:
Here, we first multiply 9 by 2 and then square the result.
- Step 1: Compute \( 9 \times 2 \)
\[ 9 \times 2 = 18 \]
- Step 2: Square the result
\[ 18^2 = 324 \]
So, \( (9 \times 2)^2 = 324 \).
- Step 1: Compute \( 9 \times 2 \)
Understanding these different interpretations helps in solving and clarifying mathematical expressions accurately. Each approach yields a unique result, emphasizing the importance of clear communication in mathematics.
Understanding Exponents in Mathematics
Exponents are a fundamental concept in mathematics, representing repeated multiplication of a number by itself. Understanding exponents is crucial for interpreting expressions like "9 2 squared". Here, we’ll break down the concept of exponents and demonstrate how they are used in various mathematical contexts.
An exponent is written as a small number above and to the right of a base number, indicating how many times the base number is multiplied by itself. For example, in the expression \( 2^3 \), 2 is the base and 3 is the exponent.
Key Concepts of Exponents
- Base: The number that is multiplied by itself. In \( a^n \), \( a \) is the base.
- Exponent: The number that indicates how many times the base is multiplied by itself. In \( a^n \), \( n \) is the exponent.
- Power: The result of the base raised to the exponent. For example, \( 2^3 \) equals 8.
Examples of Exponents
Here are a few examples to illustrate how exponents work:
- Square (Exponent of 2):
When the exponent is 2, it is called "squared." For example:
- \[ 3^2 = 3 \times 3 = 9 \]
- \[ 4^2 = 4 \times 4 = 16 \]
- Cube (Exponent of 3):
When the exponent is 3, it is called "cubed." For example:
- \[ 2^3 = 2 \times 2 \times 2 = 8 \]
- \[ 5^3 = 5 \times 5 \times 5 = 125 \]
- Higher Powers:
Exponents can be any positive integer. For example:
- \[ 2^4 = 2 \times 2 \times 2 \times 2 = 16 \]
- \[ 10^5 = 10 \times 10 \times 10 \times 10 \times 10 = 100,000 \]
Special Cases of Exponents
- Exponent of 1: Any number raised to the power of 1 is itself. For example:
- \[ 7^1 = 7 \]
- \[ 12^1 = 12 \]
- Exponent of 0: Any number raised to the power of 0 is 1. For example:
- \[ 5^0 = 1 \]
- \[ 123^0 = 1 \]
Application of Exponents in "9 2 Squared"
In the expression "9 2 squared", understanding exponents is crucial. The term "squared" indicates an exponent of 2, meaning the number is multiplied by itself. When interpreting \( 2^2 \), we perform the calculation as follows:
- \[ 2^2 = 2 \times 2 = 4 \]
This calculation forms the basis for interpreting "9 2 squared" in different ways, as seen in the earlier section.
By mastering exponents, you can simplify complex mathematical problems and clearly interpret expressions like "9 2 squared."
Order of Operations: PEMDAS/BODMAS Explained
To correctly evaluate mathematical expressions like "9 2 squared", understanding the order of operations is essential. The order of operations, often remembered by the acronyms PEMDAS or BODMAS, helps ensure that expressions are solved consistently and correctly. Let's break down these acronyms and see how they guide us in solving complex expressions.
What Do PEMDAS and BODMAS Stand For?
Both acronyms serve the same purpose but are used in different parts of the world. Here's what they represent:
| Acronym | Meaning |
|---|---|
| PEMDAS |
|
| BODMAS |
|
In both PEMDAS and BODMAS, the sequence indicates the order in which different parts of a mathematical expression should be solved:
- Parentheses/Brackets: Solve expressions inside parentheses or brackets first.
- Exponents/Orders: Next, solve any exponents or powers.
- Multiplication and Division: Perform these operations from left to right as they appear in the expression.
- Addition and Subtraction: Finally, perform these operations from left to right.
Applying PEMDAS/BODMAS to "9 2 Squared"
Let's apply these rules to the expression "9 2 squared". This can be interpreted as \( 9 \times 2^2 \). Using PEMDAS/BODMAS:
- Exponents/Orders: Calculate the exponent first:
\[ 2^2 = 4 \]
- Multiplication: Then, multiply the result by 9:
\[ 9 \times 4 = 36 \]
Therefore, using the order of operations, \( 9 \times 2^2 = 36 \).
Common Pitfalls and Tips
- Misinterpreting Parentheses: Ensure all operations within parentheses are completed first, regardless of their complexity.
- Order Matters: Multiplication and division, as well as addition and subtraction, are performed from left to right. Do not assume multiplication always comes before division.
- Double-Check Exponents: Be careful with the placement of exponents to avoid miscalculation.
By following PEMDAS/BODMAS, you can approach and solve mathematical expressions like "9 2 squared" with confidence and accuracy. These rules simplify the process, ensuring you arrive at the correct result every time.
Interpreting "9 2 Squared": Multiple Perspectives
The expression "9 2 squared" can be interpreted in various ways, leading to different results depending on the mathematical approach used. Understanding these perspectives is crucial for accurately solving such expressions. Let's explore the primary interpretations of "9 2 squared" and see how they differ.
Primary Interpretations
-
Interpretation 1: \( 9 \times 2^2 \)
In this interpretation, the exponentiation is performed first, followed by the multiplication. Using the order of operations (PEMDAS/BODMAS), we solve the exponent before multiplication:
- Step 1: Calculate \( 2^2 \)
\[ 2^2 = 4 \]
- Step 2: Multiply the result by 9
\[ 9 \times 4 = 36 \]
Therefore, \( 9 \times 2^2 = 36 \).
- Step 1: Calculate \( 2^2 \)
-
Interpretation 2: \( (9 \times 2)^2 \)
In this interpretation, the multiplication is performed first, followed by squaring the result. This approach considers the entire product inside parentheses before applying the exponent:
- Step 1: Multiply 9 by 2
\[ 9 \times 2 = 18 \]
- Step 2: Square the result
\[ 18^2 = 324 \]
Thus, \( (9 \times 2)^2 = 324 \).
- Step 1: Multiply 9 by 2
Visualizing the Differences
To better understand how these interpretations differ, consider the following comparisons:
| Expression | Steps | Result |
|---|---|---|
| \( 9 \times 2^2 \) |
|
36 |
| \( (9 \times 2)^2 \) |
|
324 |
Choosing the Correct Interpretation
The correct interpretation depends on the context in which the expression is used or how it is presented. Without parentheses, the conventional approach following PEMDAS/BODMAS rules would prioritize the exponentiation first (as in \( 9 \times 2^2 \)). However, if parentheses are explicitly provided, they dictate the sequence of operations.
Implications in Mathematics
Recognizing and correctly interpreting expressions like "9 2 squared" is essential for solving mathematical problems accurately. This understanding not only helps in academic settings but also in practical applications where precise calculations are required.
By appreciating these multiple perspectives, we gain a deeper insight into how mathematical expressions can be flexibly interpreted and solved.
Detailed Calculation for \( 9 \times 2^2 \)
The expression \( 9 \times 2^2 \) involves both multiplication and exponentiation. To solve it accurately, we follow the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction).
Let's break down the steps to calculate \( 9 \times 2^2 \) in detail:
-
Step 1: Identify the operations.
In the expression \( 9 \times 2^2 \), we have multiplication (\( \times \)) and exponentiation (\(^2\)). According to PEMDAS, we perform the exponentiation before multiplication.
-
Step 2: Calculate the exponent \( 2^2 \).
Exponentiation means multiplying the base (2) by itself as many times as indicated by the exponent (2).
- \[ 2^2 = 2 \times 2 = 4 \]
So, \( 2^2 \) equals 4.
-
Step 3: Multiply the result by 9.
Now that we have evaluated \( 2^2 \) as 4, we can proceed with the multiplication:
- \[ 9 \times 4 = 36 \]
Therefore, \( 9 \times 2^2 \) equals 36.
Summarizing the calculation:
| Step | Operation | Result |
|---|---|---|
| 1 | Identify operations (Exponentiation and Multiplication) | N/A |
| 2 | Calculate \( 2^2 \) | 4 |
| 3 | Multiply by 9 | 36 |
Thus, the detailed calculation for \( 9 \times 2^2 \) is straightforward once we follow the order of operations, leading us to the final result of 36.
Understanding and applying these steps ensures clarity and accuracy in solving mathematical expressions involving exponents and multiplication.
Detailed Calculation for \( (9 \times 2)^2 \)
The expression \( (9 \times 2)^2 \) involves both multiplication and exponentiation, but it is enclosed in parentheses. This means we must solve the operation inside the parentheses first before applying the exponent. Let’s break down the steps in detail:
-
Step 1: Evaluate the expression inside the parentheses.
First, we perform the multiplication within the parentheses:
- \[ 9 \times 2 = 18 \]
So, \( 9 \times 2 \) equals 18.
-
Step 2: Apply the exponent to the result.
Next, we need to square the result from Step 1. Squaring means multiplying the number by itself:
- \[ 18^2 = 18 \times 18 = 324 \]
Therefore, \( 18^2 \) equals 324.
Summarizing the calculation:
| Step | Operation | Result |
|---|---|---|
| 1 | Multiply 9 by 2 | 18 |
| 2 | Square the result | 324 |
Thus, the detailed calculation for \( (9 \times 2)^2 \) follows these steps to arrive at the final result of 324.
Understanding the importance of parentheses and the order of operations ensures that we solve expressions accurately, especially when they involve both multiplication and exponentiation.
Common Misinterpretations and Clarifications
The expression "9 2 squared" can be interpreted in various ways, leading to common misunderstandings. To avoid confusion, it's important to clarify the correct approach to evaluating such expressions and understand the typical mistakes that can occur. Here, we discuss these misinterpretations and provide detailed clarifications.
Misinterpretation 1: Misplacing the Exponent
One common mistake is misunderstanding where the exponent applies. For example, in the expression \( 9 \times 2^2 \), some might mistakenly believe the exponent applies to both 9 and 2. Let's break this down:
-
Incorrect Interpretation: \( (9 \times 2)^2 \)
This assumes that both 9 and 2 are multiplied first, then squared:
- \[ 9 \times 2 = 18 \]
- \[ 18^2 = 324 \]
While this calculation is mathematically correct for the expression \( (9 \times 2)^2 \), it does not apply to \( 9 \times 2^2 \). The proper order should follow PEMDAS/BODMAS rules.
-
Correct Interpretation: \( 9 \times (2^2) \)
Here, we follow the correct order of operations:
- First, evaluate the exponent:
- \[ 2^2 = 4 \]
- Then, multiply by 9:
- \[ 9 \times 4 = 36 \]
Misinterpretation 2: Ignoring Parentheses
Another frequent error is ignoring parentheses, which can drastically change the outcome of the calculation. Consider the difference between \( 9 \times 2^2 \) and \( (9 \times 2)^2 \):
-
Without Parentheses: \( 9 \times 2^2 \)
This should be evaluated as:
- First, compute the exponent:
- \[ 2^2 = 4 \]
- Then, multiply by 9:
- \[ 9 \times 4 = 36 \]
-
With Parentheses: \( (9 \times 2)^2 \)
This changes the sequence of operations:
- First, perform the multiplication inside the parentheses:
- \[ 9 \times 2 = 18 \]
- Then, apply the exponent:
- \[ 18^2 = 324 \]
Misinterpretation 3: Multiplication Order
Sometimes, the order of multiplication and exponentiation is misunderstood. It is crucial to recognize that exponentiation takes precedence over multiplication unless parentheses indicate otherwise:
-
Incorrectly Prioritizing Multiplication:
Assuming multiplication should be done first can lead to errors:
- If evaluated as \( (9 \times 2)^2 \), we first multiply then square:
- \[ 9 \times 2 = 18 \]
- \[ 18^2 = 324 \]
-
Correctly Following Order of Operations:
Exponentiation should be done before multiplication:
- First, compute \( 2^2 \):
- \[ 2^2 = 4 \]
- Then, multiply by 9:
- \[ 9 \times 4 = 36 \]
Summary of Clarifications
To avoid common misinterpretations, remember these key points:
- Always follow the order of operations (PEMDAS/BODMAS).
- Parentheses determine the sequence of operations, overriding the standard order.
- Exponentiation is performed before multiplication unless parentheses indicate otherwise.
- Carefully apply exponents only to the numbers they directly follow.
By adhering to these rules, you can accurately interpret and solve expressions like "9 2 squared" without confusion.
Practical Applications of Exponentiation
Exponentiation is a fundamental mathematical operation that has numerous practical applications in various fields. Below, we explore some of the key areas where exponentiation is applied:
-
Science and Engineering:
In science and engineering, exponentiation is used to model exponential growth and decay processes. For example, radioactive decay, population growth, and compound interest calculations all utilize exponential functions.
Example: The decay of a radioactive substance can be described by the formula \( N(t) = N_0 e^{-\lambda t} \), where \( N_0 \) is the initial quantity, \( \lambda \) is the decay constant, and \( t \) is time.
-
Finance:
Exponentiation is crucial in finance for calculating compound interest and analyzing investments. The compound interest formula is given by:
\[ A = P \left(1 + \frac{r}{n}\right)^{nt} \]
Where \( A \) is the amount of money accumulated after \( n \) years, including interest, \( P \) is the principal amount, \( r \) is the annual interest rate, \( n \) is the number of times interest is compounded per year, and \( t \) is the time in years.
-
Computer Science:
In computer science, exponentiation is used in algorithms, cryptography, and data structures. For example, the efficiency of algorithms is often expressed using Big O notation, which can involve exponential terms.
Example: Exponential growth is evident in binary trees, where the number of nodes at depth \( d \) is \( 2^d \).
-
Physics:
Exponentiation appears in various physical laws and formulas. One common example is the inverse-square law, which states that a specified physical quantity is inversely proportional to the square of the distance from the source.
Example: The intensity of light or radiation from a point source follows the inverse-square law, \( I \propto \frac{1}{r^2} \), where \( I \) is the intensity and \( r \) is the distance from the source.
-
Biology:
Exponentiation helps model biological processes such as population dynamics, enzyme reactions, and the spread of diseases. The logistic growth model, for instance, is a common application in ecology.
Example: The population growth can be described using the logistic equation: \( P(t) = \frac{K}{1 + \frac{K - P_0}{P_0}e^{-rt}} \), where \( P(t) \) is the population at time \( t \), \( K \) is the carrying capacity, \( P_0 \) is the initial population, and \( r \) is the growth rate.
As demonstrated, exponentiation is a versatile mathematical tool that is indispensable across a wide range of disciplines. Understanding its applications helps in grasping complex concepts and solving real-world problems efficiently.
Exploring More Complex Mathematical Expressions
Building on the understanding of basic exponentiation, we can explore more complex mathematical expressions involving exponents. This section will delve into various scenarios and provide detailed explanations using MathJax to enhance comprehension.
-
Expression involving multiple exponents:
Consider the expression \( (2^3)^2 \). Here, we apply the power of a power rule, which states that \((a^m)^n = a^{m \cdot n}\). Thus,
\[
(2^3)^2 = 2^{3 \cdot 2} = 2^6 = 64
\] -
Expressions with different bases:
When we have an expression like \( 3^2 \cdot 4^2 \), we can use the property of exponents that states \((a \cdot b)^n = a^n \cdot b^n\). Here,
\[
3^2 \cdot 4^2 = (3 \cdot 4)^2 = 12^2 = 144
\] -
Using parentheses to clarify operations:
Consider \( (2 \cdot 3)^2 \) versus \( 2 \cdot 3^2 \). These two expressions yield different results:
-
\((2 \cdot 3)^2\) means we first multiply 2 and 3, then square the result:
\[
(2 \cdot 3)^2 = 6^2 = 36
\] -
\(2 \cdot 3^2\) means we first square 3, then multiply by 2:
\[
2 \cdot 3^2 = 2 \cdot 9 = 18
\]
-
-
Expressions with negative bases:
For negative bases, the placement of parentheses is crucial. For instance, \((-2)^3\) and \(-2^3\) yield different results:
-
\((-2)^3\) means we cube -2:
\[
(-2)^3 = -2 \cdot -2 \cdot -2 = -8
\] -
\(-2^3\) means we first cube 2, then apply the negative sign:
\[
-2^3 = -(2^3) = -8
\]
-
-
Combining exponents and roots:
When combining exponents and roots, such as \( \sqrt{(3^2)} \), we simplify inside the root first:
\[
\sqrt{(3^2)} = \sqrt{9} = 3
\]Alternatively, \( ( \sqrt{3} )^2 \) simplifies as:
\[
( \sqrt{3} )^2 = 3
\] -
Exponents with fractional powers:
Fractional exponents denote roots. For example, \( 8^{1/3} \) represents the cube root of 8:
\[
8^{1/3} = \sqrt[3]{8} = 2
\]Another example is \( 16^{3/4} \), which involves both a root and an exponentiation:
\[
16^{3/4} = (\sqrt[4]{16})^3 = 2^3 = 8
\]
By exploring these examples, we gain a deeper understanding of how exponents can be manipulated and combined in more complex mathematical expressions.
Conclusion: Clear Interpretation in Mathematical Expressions
Interpreting mathematical expressions accurately is crucial for ensuring precise calculations and avoiding misunderstandings. The expression \(9 \times 2^2\) serves as an excellent example of the importance of clarity in mathematical notation and the application of the order of operations.
Here are some key takeaways to ensure clear interpretation in mathematical expressions:
- Use Parentheses for Clarity: Always use parentheses to clearly indicate which operations should be performed first. For instance, \( (9 \times 2)^2 \) is different from \( 9 \times 2^2 \).
- Follow the Order of Operations: Remember PEMDAS/BODMAS rules (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) to perform calculations in the correct order.
- Consistency in Notation: Use consistent notation to avoid confusion. For example, write exponents clearly and use parentheses to group terms appropriately.
- Check Your Work: Double-check calculations and interpretations, especially in complex expressions, to ensure accuracy.
By adhering to these principles, mathematical expressions can be interpreted and solved correctly, ensuring clear communication and precise results in both academic and practical applications.
Video giải thích biểu đồ dư, hệ số tương quan r và r bình phương trong phân tích dữ liệu, giúp bạn hiểu rõ hơn về cách sử dụng chúng trong thống kê.
9 2 Giải thích biểu đồ dư, r và r bình phương
READ MORE:
Video giải thích các số bình phương và lập phương trong nhóm 2, giúp bạn hiểu rõ hơn về khái niệm này trong toán học.
Câu hỏi 9 MM: Nhóm 2 - các số bình phương và lập phương








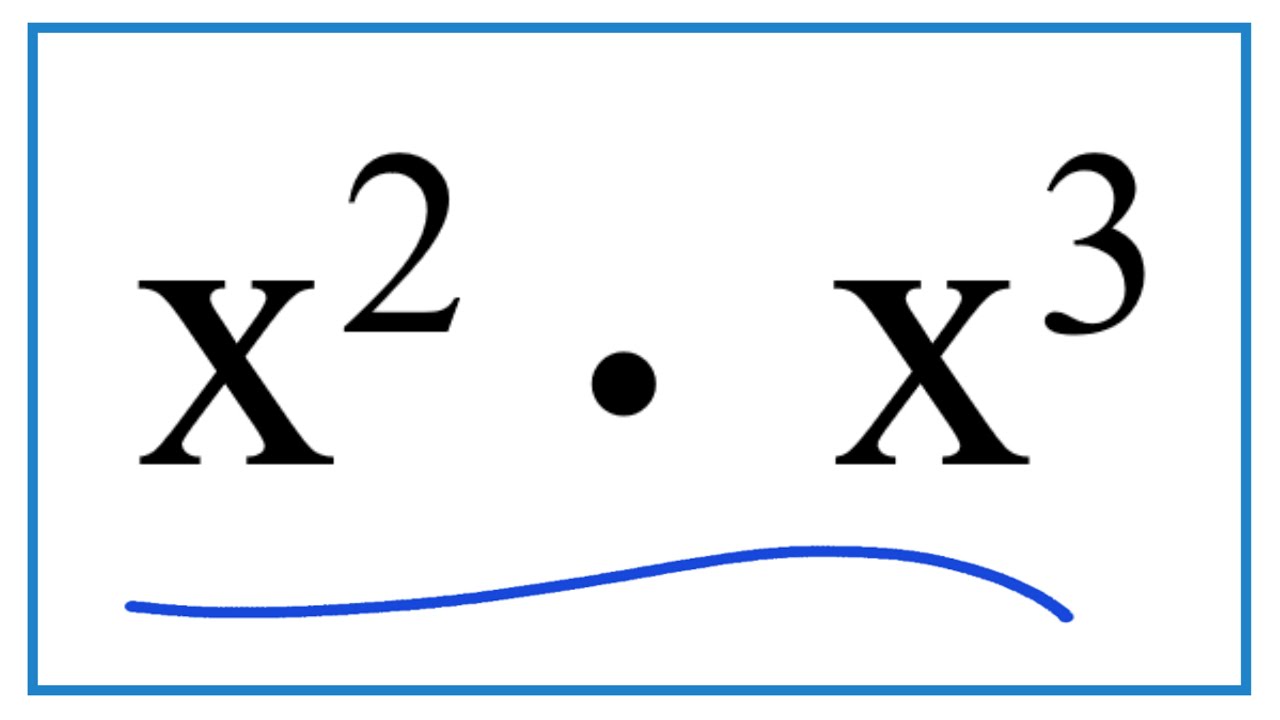



x-1=sec(squared)x.jpg)
