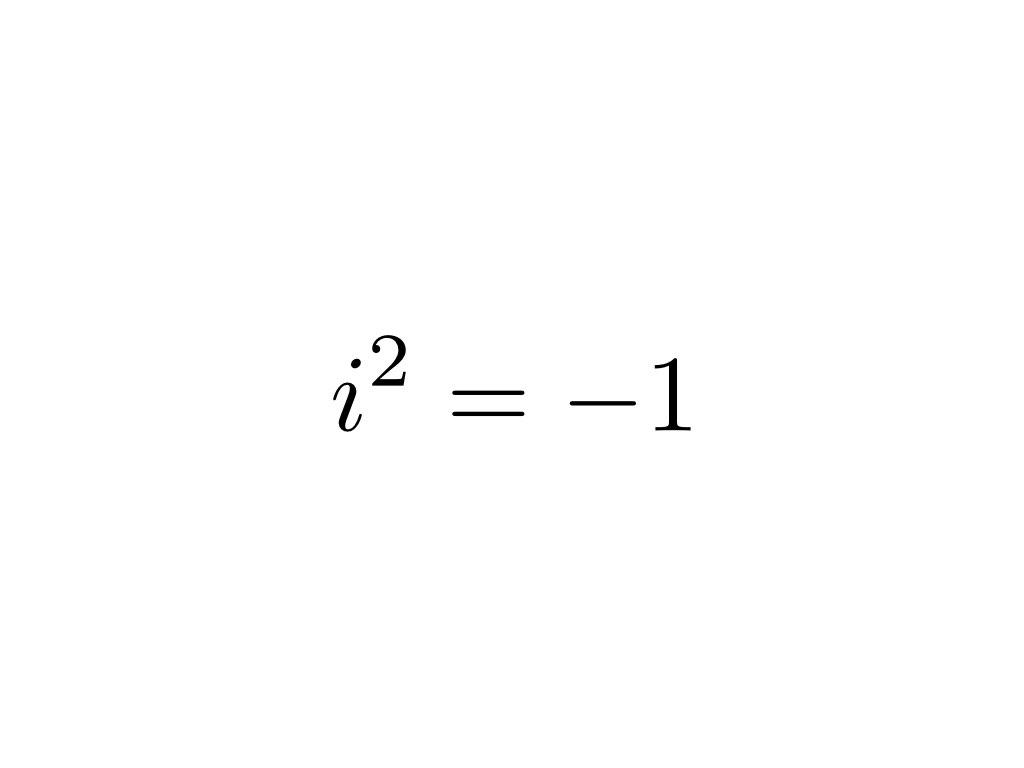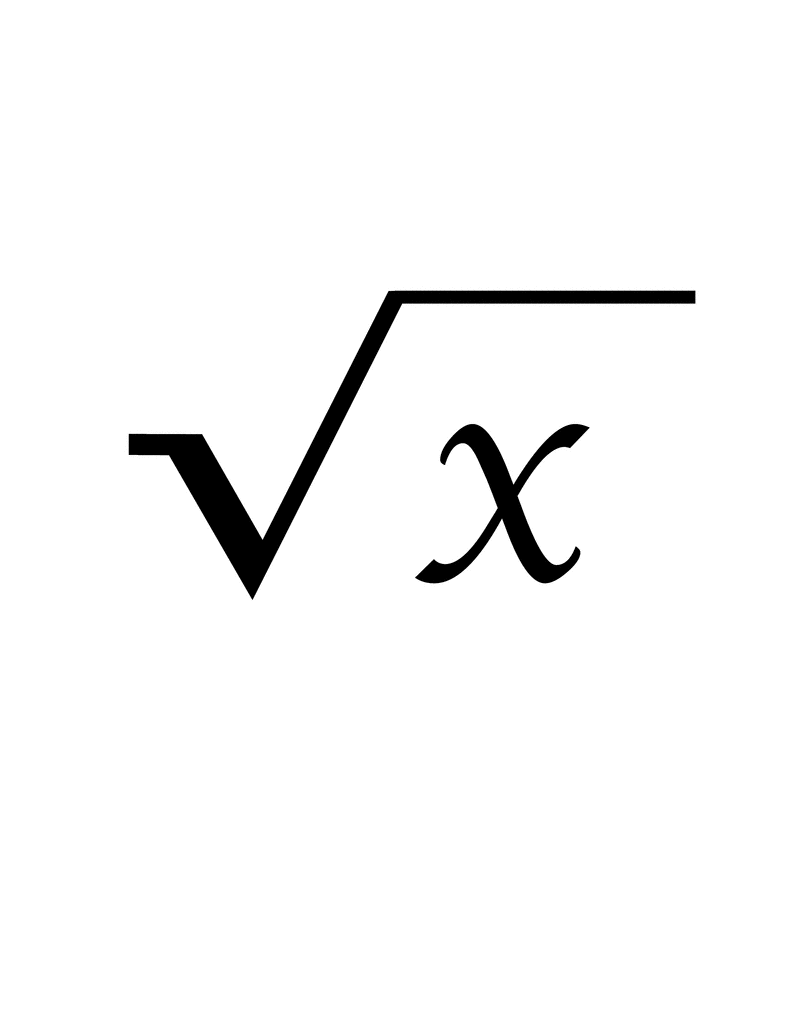1 Square Root 2 - Ultimate Guide to Understanding and Applications

The square root of 2, often written as \( \sqrt{2} \), is a number that, when multiplied by itself, equals 2. This value is approximately 1.414213562, and it is an irrational number, meaning it cannot be expressed exactly as a simple fraction.

Calculation Methods

There are various methods to calculate the square root of 2, including iterative algorithms and the use of calculators.

• Iterative Methods

  The Babylonian method, also known as Heron's method, is a classic iterative approach to finding square roots:

  1. Start with an initial guess \( y_1 = 1 \).
  2. Use the formula \( y_{n+1} = \frac{x/y_n + y_n}{2} \) to find better approximations.
  3. Continue the iterations until the desired accuracy is achieved.

  For example:

  Iteration 1:	\( y_1 = \frac{2 + 1}{2} = 1.5 \)
  Iteration 2:	\( y_2 = \frac{4/3 + 3/2}{2} = 1.4166 \)
  Iteration 3:	\( y_3 = \frac{24/17 + 17/12}{2} = 1.414215 \)

• Using Calculators

  Many online calculators can quickly compute the square root of 2. For instance:

Applications and Examples

The square root of 2 appears in various mathematical contexts and real-world applications:

• Geometry

  In geometry, the diagonal of a square with side length 1 unit is \( \sqrt{2} \) units. This follows from the Pythagorean theorem.

  Example: The length of the diagonal of a square with side 2 units is \( 2\sqrt{2} \approx 2.828 \) units.

• Algebra

  The square root of 2 is often used in algebraic equations and expressions involving radicals.

Interesting Facts

• The square root of 2 is the first known irrational number, discovered by the ancient Greeks.
• The precise decimal representation of \( \sqrt{2} \) extends infinitely without repeating.

Related Resources

The concept of 1 square root 2 encompasses a variety of mathematical principles and applications. It refers specifically to the square root of 2, often denoted as \( \sqrt{2} \), which is an irrational number approximately equal to 1.414213562. This guide aims to provide a comprehensive understanding of \( \sqrt{2} \) through a detailed exploration of its properties, calculations, and uses in different areas of mathematics and beyond.

In this guide, you will learn about:

• The definition and properties of square roots
• Methods for calculating \( \sqrt{2} \)
• Applications of \( \sqrt{2} \) in geometry and algebra
• Iterative methods for approximating square roots
• Using online calculators and tools for square root calculations
• The importance of perfect squares and higher-order roots
• Interactive learning tools and practice resources

We will start with the fundamental concepts, gradually advancing to more complex applications and calculations, ensuring a thorough grasp of the subject matter. Whether you are a student, educator, or math enthusiast, this guide will enhance your understanding and appreciation of the significance of \( \sqrt{2} \) in mathematics.

The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). Mathematically, this is expressed as:

\[
\sqrt{x} = y \quad \text{if and only if} \quad y^2 = x
\]

The square root of 2, denoted as \( \sqrt{2} \), is an important irrational number in mathematics. It cannot be expressed as a simple fraction and has an approximate decimal value of 1.414213562. This number is significant in various fields, including geometry, algebra, and number theory.

Key properties of \( \sqrt{2} \) include:

• Irrationality: \( \sqrt{2} \) cannot be exactly represented as a fraction of two integers. It has an infinite, non-repeating decimal expansion.
• Non-terminating Decimal: The decimal representation of \( \sqrt{2} \) is non-terminating and non-repeating, which is a characteristic of all irrational numbers.
• Relationship to Pythagorean Theorem: In a right-angled triangle with both legs of length 1, the hypotenuse is \( \sqrt{2} \). This follows from the Pythagorean theorem: \[ a^2 + b^2 = c^2 \quad \Rightarrow \quad 1^2 + 1^2 = c^2 \quad \Rightarrow \quad c = \sqrt{2} \]

To calculate \( \sqrt{2} \), several methods can be used:

1. Manual Calculation: Methods such as the Babylonian method (or Heron's method) allow iterative approximation of square roots. For \( \sqrt{2} \), start with an initial guess (e.g., 1.5) and refine it using the formula: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{2}{x_n} \right) \]
2. Calculator: Modern calculators can compute \( \sqrt{2} \) directly with high precision.

Understanding \( \sqrt{2} \) provides a foundation for more advanced mathematical topics and practical applications in various scientific fields.

The square root of 2, denoted as √2, is an irrational number approximately equal to 1.414. Here are methods to calculate it:

1. Manual Calculation:

   To manually find √2, iterative methods like the Babylonian method or digit-by-digit calculation can be employed. For instance:

   Step 1:	Start with an initial guess, e.g., 1.4.
   Step 2:	Iterate using the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{2}{x_n} \right) \).
   Step 3:	Repeat until desired precision is achieved.

2. Calculator Method:

   Most scientific calculators include a square root function. Simply input 2 and press the √x button to obtain the result, typically 1.414213562.

3. Numerical Methods:

   Computational methods like Newton-Raphson iteration can also be used to approximate √2 to a high degree of accuracy.

Understanding these methods provides insights into both the theoretical and practical aspects of calculating the square root of 2.

The square root of 2 (√2 ≈ 1.414) plays a significant role in various geometric applications:

• Diagonal of a Square:

  In a square with side length 1 unit, the length of the diagonal can be calculated using the formula \( \text{diagonal} = s \sqrt{2} \), where \( s \) is the side length. For example, a square with sides of length 1 unit has a diagonal length of approximately 1.414 units.

• Rectangle Diagonals:

  In rectangles, especially those with sides in a ratio of 1:√2, the diagonal length can be found using the Pythagorean theorem, highlighting the relationship between side lengths and diagonals.

• Geometric Constructions:

  Using √2 allows for geometric constructions that involve creating angles or shapes with specific proportional relationships, enhancing precision and accuracy in architectural and engineering drawings.

These applications illustrate how the square root of 2 is fundamental in solving geometric problems and designing structures with optimal proportions.

Iterative methods are crucial for approximating the square root of 2 (√2 ≈ 1.414) with increasing accuracy:

1. Babylonian Method:

   Also known as Heron's method, it involves repeatedly averaging a number with its reciprocal until convergence. The iterative formula is:

   Step 1:	Start with an initial guess \( x_0 \).
   Step 2:	Iterate using the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{2}{x_n} \right) \).
   Step 3:	Repeat until the desired precision is achieved.

2. Newton-Raphson Method:

   This method uses the derivative of a function to iteratively converge on the square root. For \( f(x) = x^2 - 2 \), the iterative formula is:

   Step 1:	Start with an initial guess \( x_0 \).
   Step 2:	Iterate using the formula: \( x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \), where \( f'(x) \) is the derivative of \( f(x) \).
   Step 3:	Continue until convergence to √2.

These iterative approaches provide systematic ways to compute the square root of 2, demonstrating the importance of numerical methods in mathematics and engineering.

The square root of 2 (√2 ≈ 1.414) appears frequently in algebraic equations, particularly in quadratic equations and expressions involving the plus-minus symbol:

• Quadratic Equations:

  Quadratic equations of the form \( ax^2 + bx + c = 0 \) often involve square roots, such as solutions \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \). When \( b^2 - 4ac = 0 \), the solutions are rational and may include √2.

• Complex Numbers:

  Involving square roots in algebra can lead to complex numbers, where √2 is a fundamental component in defining their magnitude and phase.

• Symbolic Representation:

  The symbol √2 represents the principal (positive) square root of 2 in algebraic expressions. It signifies both the mathematical concept and the numerical value that arises in various computations.

Understanding the role of √2 in algebra enriches comprehension of equations, especially those involving quadratic forms and complex numbers.

Various online tools and calculators are available for accurate and efficient calculations involving the square root of 2 (√2 ≈ 1.414):

• Basic Calculators:

  Standard online calculators provide simple square root functionality. Users can input 2 and obtain the square root directly.

• Scientific Calculators:

  Advanced calculators, including scientific and graphing calculators, offer precise √x functions suitable for complex mathematical operations.

• Mobile Apps:

  Many mobile applications provide square root calculations on the go, offering convenience for students, professionals, and enthusiasts.

• Website Plugins:

  Plugins embedded in educational websites or forums facilitate square root calculations, often integrated into learning modules and interactive tools.

These tools enhance accessibility and accuracy in computing the square root of 2, catering to diverse user needs across different platforms.

Perfect squares are numbers that can be expressed as the square of an integer. For example, the numbers 1, 4, 9, 16, and 25 are perfect squares because they can be written as \(1^2\), \(2^2\), \(3^2\), \(4^2\), and \(5^2\), respectively.

To identify and simplify perfect squares:

1. Identify if the number is a perfect square by finding its integer square root. For instance, 36 is a perfect square because \(\sqrt{36} = 6\).
2. If the number is not a perfect square, simplify it by expressing it as a product of its prime factors and then pairing the factors. For example, \(\sqrt{72} = \sqrt{2^3 \cdot 3^2} = 6\sqrt{2}\).

Higher order roots extend the concept of square roots to cubes, fourth roots, and beyond. Here are some key points and methods for calculating higher order roots:

• Cubic Roots: The cube root of a number \(a\) is a number \(b\) such that \(b^3 = a\). For example, \(\sqrt[3]{27} = 3\) because \(3^3 = 27\).
• Fourth Roots: The fourth root of a number \(a\) is a number \(b\) such that \(b^4 = a\). For instance, \(\sqrt[4]{16} = 2\) because \(2^4 = 16\).

The general formula for the \(n\)th root of a number \(a\) is given by:

\[\sqrt[n]{a} = a^{\frac{1}{n}}\]

To find higher order roots:

1. Use a calculator with root functions or an online tool that supports \(n\)th roots.
2. For manual calculations, factor the number and then apply the root to each factor. For example, to find the fourth root of 81, we recognize that \(81 = 3^4\), so \(\sqrt[4]{81} = 3\).

When dealing with perfect squares and higher order roots, it's useful to understand their applications in various mathematical contexts:

• Geometry: Calculating areas and volumes where roots are involved, such as determining the side length of a square with a given area.
• Algebra: Solving polynomial equations where roots are used to find solutions, such as in quadratic and cubic equations.
• Engineering: Understanding tolerances and precision measurements where square and cube roots are commonly used.

Interactive tools and practice problems can greatly enhance the understanding of perfect squares and higher order roots. Here are some resources:

• Online calculators that provide step-by-step solutions for finding roots.
• Educational apps and websites offering interactive exercises and quizzes.
• Math games and puzzles that incorporate root calculations to make learning fun and engaging.

Interactive learning tools and games are an effective way to practice and master the concept of square roots. Here are some recommended activities and resources to enhance your understanding and skills:

• Square Root Concentration Game: This game allows you to practice matching square roots with their corresponding numbers. As you pair them correctly, the cards disappear, making it a fun and engaging way to reinforce your knowledge of square roots.
• Pyramid Math 2: In this game, players calculate the square root and pick the correct marble to drop into a jar. It helps improve the speed and accuracy of square root calculations while engaging multiple cognitive skills.
• MathPup Hook Square Root: This game challenges players to guide a ball to hit the correct answer bubble for displayed square root questions. It combines motor skills with mathematical practice.
• Simplifying Square Roots: This game focuses on simplifying square roots, including irrational square roots, which helps in understanding complex expressions.
• Mathmammoth Square Root Game: This customizable game allows you to set the number of questions and time per question, offering a flexible practice environment for square root calculations.
• Square Roots Spin the Wheel Game: Players spin a wheel and answer square root questions to accumulate points. This game provides an exciting way to practice square roots with a game show format.

Additionally, platforms like Khan Academy offer structured practice problems and instructional videos on square roots and related concepts. You can find a variety of practice exercises and resources to help solidify your understanding.

Engaging with these interactive tools and games will not only make learning more enjoyable but also enhance your proficiency in calculating and understanding square roots.

Here are some common questions related to square roots, particularly focusing on the square root of 2 (√2).

• What is a perfect square number?

  A perfect square number is a number that is the square of an integer. For example, 4, 9, 16, and 25 are perfect square numbers because they can be written as 2², 3², 4², and 5², respectively.

• What is the square root symbol?

  The square root symbol is denoted as '√', also known as the radical symbol. For instance, the square root of 16 is written as √16 = 4.

• Why is the square root of 2 considered irrational?

  The square root of 2 is considered irrational because it cannot be expressed as a fraction of two integers. Its decimal representation is non-terminating and non-repeating, approximately equal to 1.41421356237...

• How can I calculate the square root of 2 manually?

  You can calculate the square root of 2 using the long division method or iterative methods such as the Newton-Raphson method. Here’s a brief outline of the long division method:
  

  
  
  1. Group the digits in pairs, starting from the decimal point.
  
  
  2. Find the largest number whose square is less than or equal to the first pair. This number is the first digit of the root.
  
  
  3. Subtract the square of this number from the first pair and bring down the next pair.
  
  
  4. Double the current root and determine the next digit by trial and error.
  
  
  5. Repeat the process for the desired number of decimal places.
  
  
  
  


• What are the practical applications of √2?

  The square root of 2 is widely used in geometry, particularly in calculating the diagonal of a square. It also appears in various mathematical and scientific contexts, including physics and engineering problems where precise measurements and calculations are essential.

• What are some interactive tools for practicing square root calculations?

  Many online calculators and educational platforms provide tools for practicing square root calculations. Websites like Symbolab, Mathway, and educational resources such as BYJU'S offer interactive calculators and tutorials to help you understand and practice square roots.

• How is the value of √2 approximated?

  Approximations of √2 can be achieved through various methods, including:
  

  
  
  • Using the decimal approximation (1.414) for quick calculations.
  
  
  • Applying iterative methods like the Newton-Raphson method to get a more precise value.
  
  
  • Using continued fractions for very accurate approximations.