Topic x squared times x cubed: Understanding the multiplication of powers is fundamental in algebra. When we multiply \( x^2 \) (x squared) and \( x^3 \) (x cubed), we use the rule of adding exponents, resulting in \( x^5 \). This principle simplifies complex expressions and is essential in higher-level math. Explore how this works and why it matters in mathematical problem-solving.
Table of Content
- Simplifying Exponents
- Introduction
- What Does "X Squared Times X Cubed" Mean?
- Breaking Down the Expression
- Examples and Applications
- Basic Concept of Exponents
- Multiplication of Powers with the Same Base
- Calculating x Squared Times x Cubed
- Applications in Mathematics
- Visual Representation of x^5
- Common Mistakes and Misconceptions
- Advanced Exponent Rules
- Examples and Practice Problems
- Conclusion
- YOUTUBE: Mô tả các thuật ngữ chính liên quan đến x, x bình phương và x lập phương trong toán học.
Simplifying Exponents
The product of x squared and x cubed can be simplified using the rules of exponents. The general rule for multiplying powers with the same base is to add their exponents.
Mathematical Explanation
Given:
Using the rule of exponents \( x^a \times x^b = x^{a+b} \):
- \( x^2 \times x^3 = x^{2+3} = x^5 \)
Steps to Simplify
- Identify the base and the exponents: \( x^2 \) and \( x^3 \).
- Add the exponents: \( 2 + 3 = 5 \).
- Combine the terms: \( x^2 \times x^3 = x^5 \).
Examples
| Expression | Result |
|---|---|
| \( x^2 \times x^3 \) | \( x^5 \) |
| \( a^4 \times a^2 \) | \( a^6 \) |
| \( b^3 \times b^5 \) | \( b^8 \) |
Visual Representation
The following graph shows the behavior of the function \( y = x^5 \) which results from the multiplication of \( x^2 \) and \( x^3 \):

Understanding how to simplify exponents is crucial in algebra and higher-level mathematics, making it easier to solve complex equations and understand polynomial expressions.
READ MORE:
Introduction
Understanding exponents is fundamental in algebra and higher mathematics. When dealing with expressions like "x squared times x cubed," it's essential to comprehend the rules of exponents to simplify and solve these equations accurately. This article will delve into the mathematical principles behind this expression and provide step-by-step explanations.
What Does "X Squared Times X Cubed" Mean?
In algebra, "x squared times x cubed" is represented as \(x^2 \times x^3\). According to the laws of exponents, when multiplying two powers that have the same base, you add the exponents. Thus, \(x^2 \times x^3 = x^{2+3} = x^5\).
Breaking Down the Expression
- Understanding Exponents: An exponent denotes how many times a number, known as the base, is multiplied by itself. For instance, \(x^2 = x \times x\) and \(x^3 = x \times x \times x\).
- Multiplying Exponents: When multiplying exponents with the same base, you add the exponents. Therefore, \(x^2 \times x^3\) becomes \(x^{2+3} = x^5\).
Examples and Applications
| Expression | Calculation | Result |
| \(x^2 \times x^3\) | \(x^{2+3}\) | \(x^5\) |
| \(2^2 \times 2^3\) | \(2^{2+3}\) | \(2^5 = 32\) |
| \(a^4 \times a^2\) | \(a^{4+2}\) | \(a^6\) |
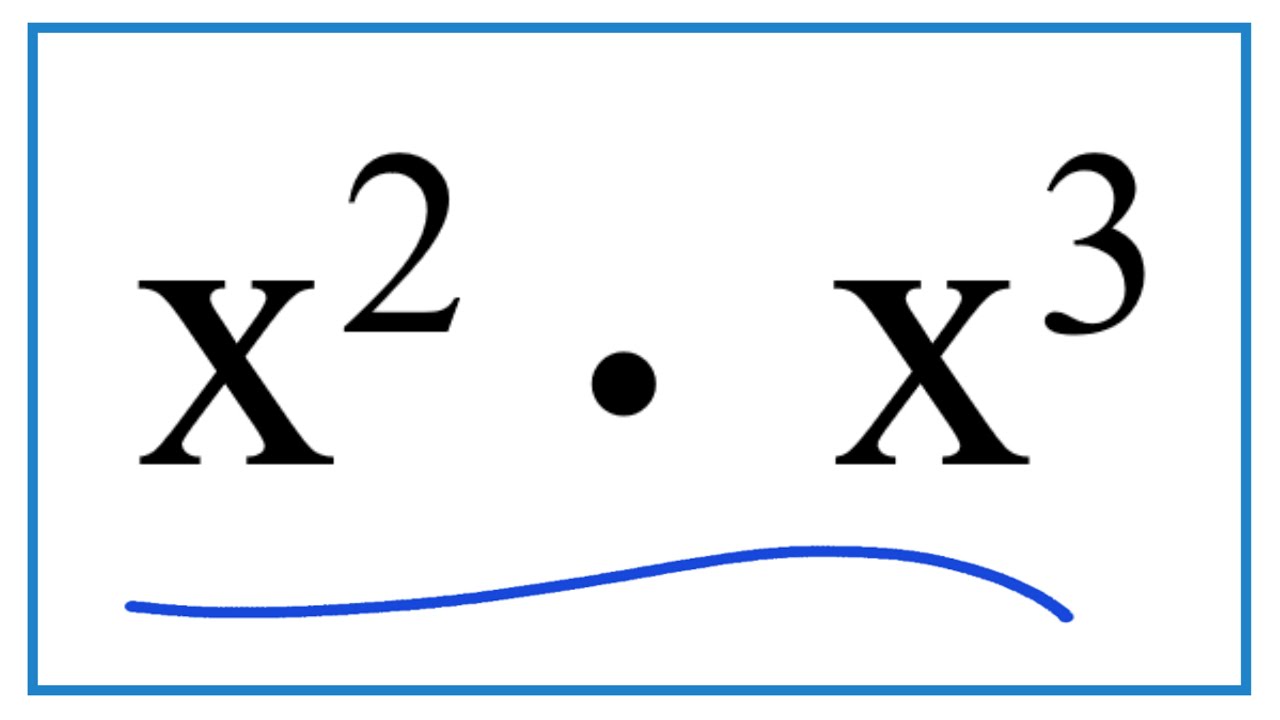
Basic Concept of Exponents
Exponents are a fundamental concept in mathematics, allowing us to express repeated multiplication in a compact form. An exponent indicates how many times a number, known as the base, is multiplied by itself. The notation \( x^n \) means that the base \( x \) is multiplied by itself \( n \) times. Here are some key points to understand the basic concept of exponents:
- When the exponent is 1, the value is the base itself: \( x^1 = x \).
- When the exponent is 0, the value is always 1 (provided the base is not zero): \( x^0 = 1 \).
- Negative exponents represent the reciprocal of the base raised to the absolute value of the exponent: \( x^{-n} = \frac{1}{x^n} \).
To perform operations with exponents, certain rules apply:
- Product of Powers: When multiplying two expressions with the same base, add the exponents: \( x^m \cdot x^n = x^{m+n} \).
- Quotient of Powers: When dividing two expressions with the same base, subtract the exponents: \( \frac{x^m}{x^n} = x^{m-n} \).
- Power of a Power: When raising an exponent to another exponent, multiply the exponents: \( (x^m)^n = x^{m \cdot n} \).
- Power of a Product: When raising a product to an exponent, apply the exponent to each factor: \( (xy)^n = x^n \cdot y^n \).
- Power of a Quotient: When raising a quotient to an exponent, apply the exponent to both the numerator and the denominator: \( \left(\frac{x}{y}\right)^n = \frac{x^n}{y^n} \).
Understanding these basic properties and rules of exponents helps simplify and solve various mathematical problems, making calculations more efficient.
Multiplication of Powers with the Same Base
When multiplying powers with the same base, you can simplify the expression by adding the exponents. This fundamental rule of exponents helps streamline complex algebraic expressions.
For example, consider the expression \( x^2 \times x^3 \). Here’s a step-by-step breakdown:
- Identify the base: Both terms have the base \( x \).
- Add the exponents: \( 2 + 3 = 5 \).
- Combine the terms: \( x^2 \times x^3 = x^{2+3} = x^5 \).
This method applies universally to any base with exponents. If you have more terms, such as \( x^a \times x^b \times x^c \), simply add all the exponents: \( x^{a+b+c} \).
Here are more examples to illustrate this rule:
- \( y^4 \times y^6 = y^{4+6} = y^{10} \)
- \( a^7 \times a^3 = a^{7+3} = a^{10} \)
- \( z^2 \times z^5 \times z^3 = z^{2+5+3} = z^{10} \)
Understanding this principle simplifies working with polynomial expressions and equations, making it easier to solve and manipulate them effectively.
Calculating x Squared Times x Cubed
To calculate \( x^2 \times x^3 \), you need to understand the rules of exponents. When multiplying powers with the same base, you simply add the exponents. Here's a step-by-step guide:
- Identify the base and the exponents. In this case, the base is \( x \), the first exponent is 2, and the second exponent is 3.
- Apply the rule for multiplying exponents with the same base: \( x^a \times x^b = x^{a+b} \).
- Add the exponents: \( 2 + 3 = 5 \).
- Combine the base with the new exponent: \( x^{2+3} = x^5 \).
Therefore, \( x^2 \times x^3 \) simplifies to \( x^5 \). This rule of adding exponents is fundamental in algebra and helps simplify expressions involving powers of the same base.
Applications in Mathematics
The expression \( x^2 \times x^3 \) is fundamental in various mathematical applications. By understanding how to handle exponents, we can delve into more complex polynomial functions and their uses in different fields.
- Physics and Engineering: In physics, the combination of quadratic and cubic terms is crucial for modeling phenomena such as projectile motion and other non-linear effects. Engineering applications often involve polynomial functions to solve problems related to structural dynamics and control systems.
- Economics: Polynomial equations, including terms like \( x^2 \) and \( x^3 \), are used to represent growth trends and economic behaviors. These equations can model accelerating growth rates and other complex economic scenarios, making them essential in economic forecasting and analysis.
- Environmental Science: Polynomial functions help in predicting changes in climate conditions, population dynamics, and the spread of pollutants. By incorporating quadratic and cubic terms, environmental models can more accurately reflect real-world conditions and phenomena.
Understanding the principles behind \( x^2 \times x^3 \) enables the application of these concepts across various disciplines, enhancing problem-solving capabilities and providing deeper insights into complex systems.
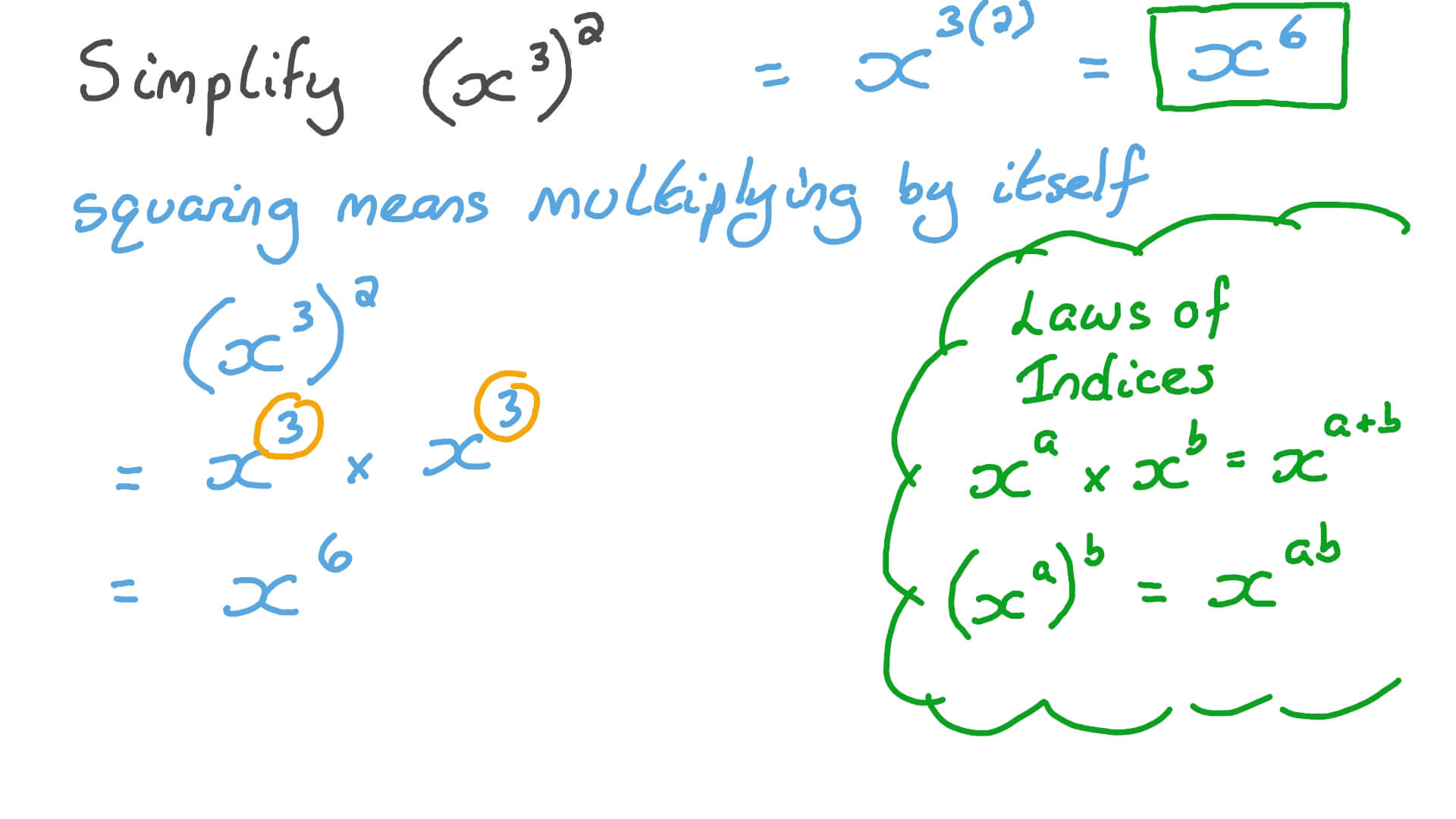
Visual Representation of x^5
Understanding the visual representation of \( x^5 \) can greatly enhance comprehension of the concept of exponents. Here are a few ways to visualize \( x^5 \) step by step:
Number Line Representation: On a number line, each multiplication by \( x \) can be seen as stretching the number line. For \( x^5 \), this means extending the line five times the unit distance.
Area Model: This method uses geometric shapes to represent multiplication. For \( x^5 \), imagine a square with side length \( x^2 \). Multiplying by \( x \) three more times extends this square into a five-dimensional space, which is more abstract but can be broken down into three-dimensional and two-dimensional projections.
Tree Diagram: In a tree diagram, each branch represents multiplication by \( x \). Starting with \( x \) at the root, each level of the tree splits into branches, representing another multiplication. The fifth level of branches gives us \( x^5 \).
Graphical Representation: On a Cartesian plane, plotting \( y = x^5 \) shows a steep curve that becomes increasingly steep as \( x \) moves away from zero. This visualizes the rapid growth rate of exponential functions.
Using these visual methods can help solidify the understanding of exponents and their applications in various mathematical contexts.
Common Mistakes and Misconceptions
When dealing with the multiplication of exponents, such as
-
Incorrect Addition of Exponents: A frequent mistake is to add the exponents incorrectly. For example, instead of correctly calculating
x^2 \times x^3 = x^{2+3} = x^5 , one might incorrectly add the bases or misinterpret the exponent addition. -
Multiplying Exponents Instead of Adding: Another common error is to multiply the exponents instead of adding them. For instance, some might mistakenly compute
x^2 \times x^3 asx^{2 \times 3} = x^6 , which is incorrect. -
Misunderstanding the Same Base Rule: It's essential to remember that the rule
a^m \times a^n = a^{m+n} only applies when the bases are the same. A common mistake is to apply this rule to different bases, such asx^2 \times y^3 , which does not simplify using exponent addition. -
Ignoring Coefficients: When coefficients are involved, like in
3x^2 \times 4x^3 , a common misconception is to ignore the coefficients and only combine the exponents. The correct approach is to multiply the coefficients and add the exponents:3 \times 4 \times x^{2+3} = 12x^5 . -
Forgetting Zero Exponents: A zero exponent means the value is 1, not 0. Misinterpreting
x^0 as 0 is a frequent mistake. The correct interpretation isx^0 = 1 . -
Handling Negative Exponents: Negative exponents indicate reciprocal values, not negative values. For example,
x^{-3} = \frac{1}{x^3} . Misinterpreting this can lead to incorrect results.
By recognizing these common mistakes and misconceptions, one can avoid errors and correctly apply exponent rules in mathematical calculations.
Advanced Exponent Rules
Understanding advanced exponent rules is essential for solving complex mathematical problems efficiently. Here are some of the key rules explained in detail:
The Power of a Power Rule
This rule states that when raising an exponent to another exponent, you multiply the exponents. Symbolically, it is expressed as:
\[
(x^m)^n = x^{m \cdot n}
\]
Example:
\[
(x^2)^3 = x^{2 \cdot 3} = x^6
\]
The Power of a Product Rule
This rule applies when raising a product to a power. The exponent is distributed to each factor within the parentheses. It is represented as:
\[
(xy)^n = x^n \cdot y^n
\]
Example:
\[
(2x^3y^2)^4 = 2^4 \cdot (x^3)^4 \cdot (y^2)^4 = 16x^{12}y^8
\]
The Power of a Quotient Rule
This rule states that when raising a quotient to a power, the exponent applies to both the numerator and the denominator:
\[
\left(\frac{x}{y}\right)^n = \frac{x^n}{y^n}
\]
Example:
\[
\left(\frac{x^2}{y^3}\right)^2 = \frac{x^{2 \cdot 2}}{y^{3 \cdot 2}} = \frac{x^4}{y^6}
\]
The Negative Exponent Rule
Negative exponents indicate reciprocals. An expression with a negative exponent can be rewritten as a fraction:
\[
x^{-n} = \frac{1}{x^n}
\]
Example:
\[
5^{-3} = \frac{1}{5^3} = \frac{1}{125}
\]
The Zero Exponent Rule
This rule states that any nonzero base raised to the power of zero equals one:
\[
x^0 = 1
\]
Example:
\[
7^0 = 1
\]
Fractional Exponents
Fractional exponents represent roots. The numerator of the fraction is the power, and the denominator is the root:
\[
x^{\frac{m}{n}} = \sqrt[n]{x^m}
\]
Example:
\[
8^{\frac{2}{3}} = \sqrt[3]{8^2} = \sqrt[3]{64} = 4
\]
Combining Rules
Often, problems require the use of multiple exponent rules. For example:
\[
\left(\frac{2x^2}{y^{-3}}\right)^4 = \frac{2^4 \cdot (x^2)^4}{(y^{-3})^4} = \frac{16x^8}{y^{-12}} = 16x^8y^{12}
\]
Mastering these rules allows for the simplification and solution of complex exponent expressions.
Examples and Practice Problems
Understanding the multiplication of exponents is crucial in many areas of mathematics. Here we will explore several examples and provide practice problems to solidify the concepts.
Examples
-
Example 1: Simplify \(x^2 \times x^3\)
Using the rule of exponents that states \(a^m \times a^n = a^{m+n}\), we get:
\[
x^2 \times x^3 = x^{2+3} = x^5
\] -
Example 2: Simplify \((2x^3) \times (3x^4)\)
First, multiply the coefficients (2 and 3), then apply the exponent rule:
\[
(2x^3) \times (3x^4) = (2 \times 3) \times (x^3 \times x^4) = 6x^{3+4} = 6x^7
\] -
Example 3: Simplify \((5x^2y^3) \times (2x^4y)\)
First, multiply the coefficients (5 and 2), then apply the exponent rule separately for \(x\) and \(y\):
\[
(5x^2y^3) \times (2x^4y) = (5 \times 2) \times (x^2 \times x^4) \times (y^3 \times y) = 10x^{2+4}y^{3+1} = 10x^6y^4
\]
Practice Problems
-
Problem 1: Simplify \(x^4 \times x^6\)
Answer: \(x^{10}\)
-
Problem 2: Simplify \((3x^5) \times (4x^2)\)
Answer: \(12x^7\)
-
Problem 3: Simplify \((7a^3b^2) \times (2a^4b^3)\)
Answer: \(14a^7b^5\)
-
Problem 4: Simplify \((6m^2n^3) \times (3m^4n^2)\)
Answer: \(18m^6n^5\)
-
Problem 5: Simplify \( (x^2y^3) \times (xy^4)\)
Answer: \(x^{2+1}y^{3+4} = x^3y^7\)
Challenge Problems
Try solving these more complex problems to test your understanding:
-
Problem 6: Simplify \((4a^2b) \times (2a^3b^4) \times (3a^2b^3)\)
Answer: \(24a^{2+3+2}b^{1+4+3} = 24a^7b^8\)
-
Problem 7: Simplify \((x^2 + x) \times (x^3 - x^2)\)
Answer: \(x^5 - x^4 + x^3 - x^2\)
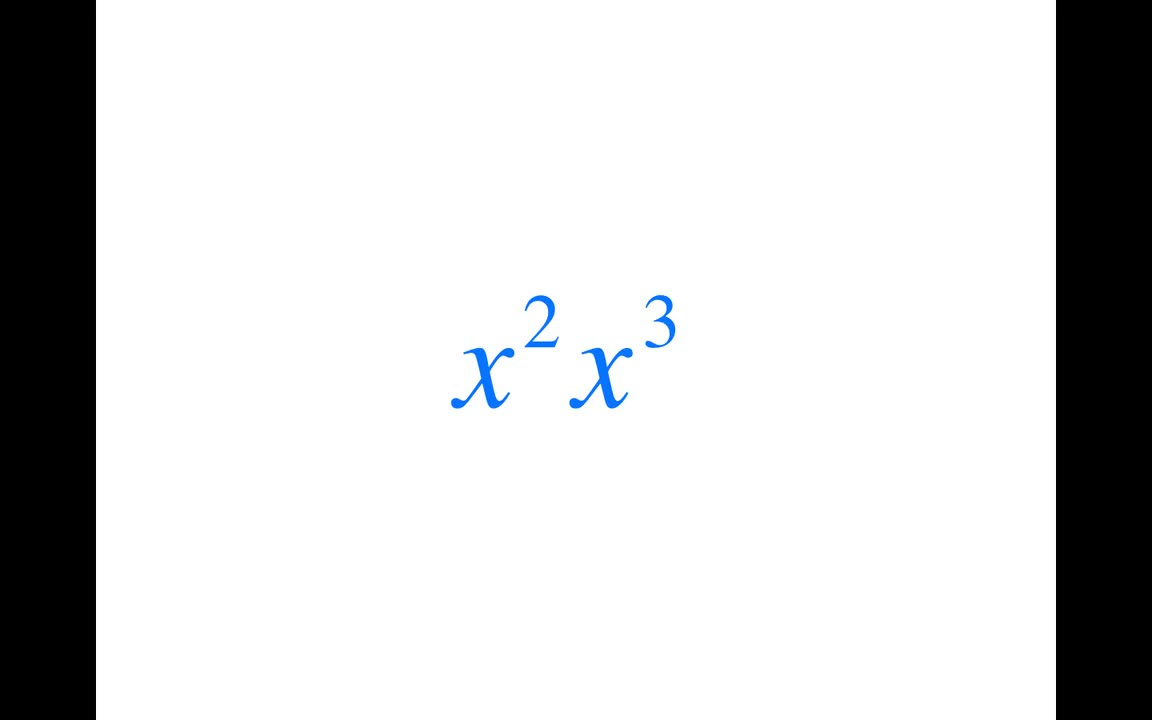
Conclusion
Understanding the multiplication of powers with the same base, such as \( x^2 \times x^3 \), is crucial in mathematics. By applying the exponent rules, we know that \( x^2 \times x^3 = x^{2+3} = x^5 \). This shows how exponents combine when multiplying like bases.
Applications of this concept are vast, from algebraic simplifications to real-world problems involving repeated multiplication. It forms a fundamental part of understanding how variables interact and grow in mathematical contexts.
Common mistakes often involve misapplying the rules of exponents or forgetting to combine like terms correctly. By practicing examples and understanding these rules thoroughly, one can avoid these pitfalls.
In conclusion, mastering the rules of exponents, including multiplication of powers with the same base, opens the door to more advanced mathematical concepts and problem-solving techniques.
Mô tả các thuật ngữ chính liên quan đến x, x bình phương và x lập phương trong toán học.
Thuật ngữ chính: Xác định ý nghĩa của x, x bình phương và x lập phương
READ MORE:
Mô tả phép tính nhân giữa x^2 và x^3 trong toán học.
Phép nhân x^2 lần x^3 (x^2 ⋅ x^3)










x-1=sec(squared)x.jpg)
