Topic simplifying non perfect square roots: Understanding how to simplify non perfect square roots is essential for tackling more complex math problems. This guide will help you master the basics by breaking down the process into easy-to-follow steps, ensuring you can confidently simplify any non perfect square root you encounter.
Table of Content
- Simplifying Non-Perfect Square Roots
- Introduction
- Table of Contents
- Definition and Basic Concepts
- Perfect Squares vs. Non-Perfect Squares
- Methods to Simplify Non-Perfect Square Roots
- Step-by-Step Simplification Process
- Examples and Practice Problems
- Common Mistakes to Avoid
- Additional Resources
- YOUTUBE: Hướng dẫn chi tiết về cách rút gọn căn bậc hai của một số không phải là số chính phương. Xem video để hiểu rõ hơn về kỹ thuật này.
Simplifying Non-Perfect Square Roots
Learning to simplify non-perfect square roots can seem challenging at first, but with practice and understanding of a few key concepts, it becomes much easier. Here's a step-by-step guide to help you through the process:
Steps to Simplify Non-Perfect Square Roots
-
Identify the Factors
First, list all factors of the number inside the square root. For example, for \( \sqrt{72} \), list the factors of 72:
- Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
-
Find the Largest Perfect Square Factor
Next, determine which of these factors are perfect squares. The largest perfect square factor of 72 is 36 (since \( 36 = 6^2 \)).
Thus, we can express 72 as the product of 36 and 2: \( 72 = 36 \times 2 \).
-
Rewrite and Simplify
Rewrite the original square root using the factors:
$$ \sqrt{72} = \sqrt{36 \times 2} $$
Apply the property of square roots, which allows us to separate the product inside the square root:
$$ \sqrt{72} = \sqrt{36} \times \sqrt{2} $$
Since \( \sqrt{36} = 6 \), we can simplify further:
$$ \sqrt{72} = 6 \sqrt{2} $$
Thus, the simplified form of \( \sqrt{72} \) is \( 6\sqrt{2} \).
Example Problems
| Expression | Steps | Result |
|---|---|---|
| \(\sqrt{48}\) |
|
\( 4\sqrt{3} \) |
| \(\sqrt{18}\) |
|
\( 3\sqrt{2} \) |
Additional Tips
- Always look for the largest perfect square factor to simplify your work.
- If there are no perfect square factors other than 1, the square root is already in its simplest form.
- Practice with different numbers to get comfortable with the process.
By following these steps and practicing regularly, simplifying non-perfect square roots will become a straightforward task.

READ MORE:
Introduction
Simplifying non-perfect square roots is an essential skill in mathematics that allows for easier manipulation and understanding of expressions involving square roots. This process involves breaking down the number inside the square root into its prime factors and identifying any perfect squares. Here, we will discuss step-by-step methods, common rules, and provide examples to illustrate how to simplify non-perfect square roots effectively.
- Identify Factors
- Prime Factorization
- Apply the Square Root Property
- Simplify
Example 1: Simplify \(\sqrt{72}\)
- Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
- Largest perfect square factor: 36
- \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)
Example 2: Simplify \(\sqrt{128}\)
- Factors of 128: 1, 2, 4, 8, 16, 32, 64, 128
- Largest perfect square factor: 64
- \(\sqrt{128} = \sqrt{64 \times 2} = \sqrt{64} \times \sqrt{2} = 8\sqrt{2}\)
Begin by listing all factors of the number under the square root. Identify which of these factors are perfect squares.
Decompose the number into its prime factors, separating out any perfect square factors.
Utilize the property \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\) to split the radical into simpler components.
Simplify the square root of the perfect square factor and multiply it by the remaining radical.
Examples
Table of Contents
Introduction
Understanding Square Roots
The Concept of Non-Perfect Square Roots
Methods to Simplify Non-Perfect Square Roots
- Identifying Perfect Square Factors
- Prime Factorization Technique
- Step-by-Step Simplification Process
Examples and Practice Problems
- Example 1: Simplifying √50
- Example 2: Simplifying √72
- Example 3: Simplifying √48
Common Mistakes to Avoid
Applications of Simplified Radicals in Real Life
Conclusion
Definition and Basic Concepts
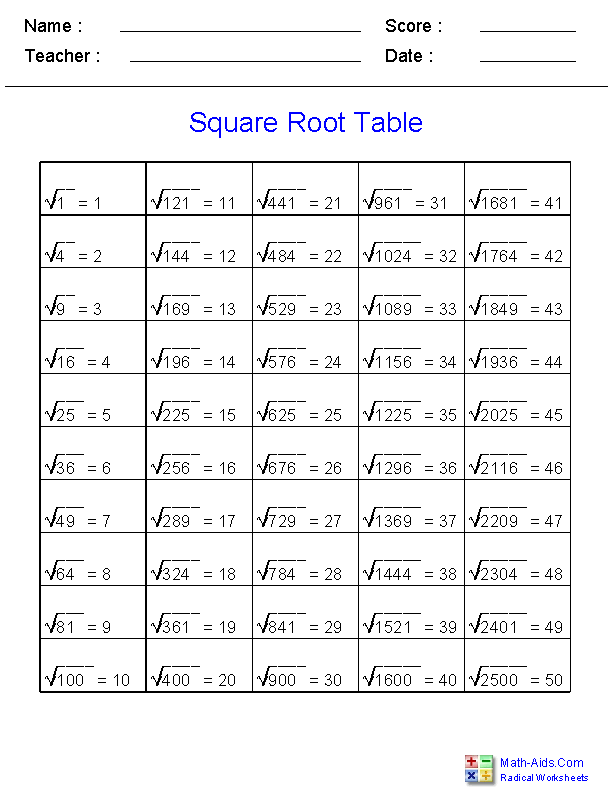
In mathematics, a square root of a number x is a number y such that y2 = x. The principal square root is the non-negative root and is denoted as √x. For example, √9 = 3 because 32 = 9.
A perfect square is an integer that is the square of another integer. Examples of perfect squares include 1, 4, 9, 16, and 25. For these numbers, their square roots are whole numbers: √1 = 1, √4 = 2, √9 = 3, and so on.
Non-perfect squares are numbers that are not the square of any integer. For example, 2, 3, 5, 7, and 10 are non-perfect squares. The square roots of these numbers are irrational numbers, which cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions. For instance, √2 ≈ 1.414, √3 ≈ 1.732.
To understand how to simplify non-perfect square roots, it's essential to know a few key concepts and rules:
-
Prime Factorization:
This method involves breaking down the number inside the square root into its prime factors. For example, 18 can be factored into 2 × 3 × 3. This helps in identifying pairs of factors that can be simplified.
-
Product Rule for Radicals:
The product rule states that the square root of a product is equal to the product of the square roots of the factors. Mathematically, √(a × b) = √a × √b. This rule is useful in separating and simplifying radicals.
-
Quotient Rule for Radicals:
The quotient rule states that the square root of a quotient is equal to the quotient of the square roots of the numerator and denominator. In mathematical terms, √(a / b) = √a / √b, where b ≠ 0. This rule helps in simplifying fractions under the square root.
These concepts form the foundation for simplifying non-perfect square roots. By applying these methods, one can break down complex radicals into simpler forms, making calculations easier and more manageable.
Perfect Squares vs. Non-Perfect Squares
Perfect squares are numbers that result from multiplying an integer by itself. They have integer square roots, meaning when you take the square root of a perfect square, you get a whole number. Examples of perfect squares include 1, 4, 9, 16, and so on.
On the other hand, non-perfect squares are numbers that are not the squares of integers. When you take the square root of a non-perfect square, you get an irrational number, which cannot be expressed as a fraction or a decimal that terminates or repeats. Examples of non-perfect squares include 2, 3, 5, and so forth.
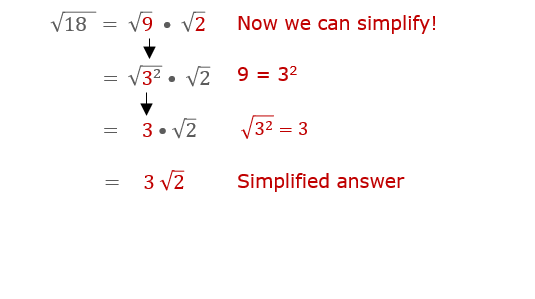
Methods to Simplify Non-Perfect Square Roots
When dealing with non-perfect square roots, there are several methods you can employ to simplify them effectively:
- Prime Factorization: Break down the number inside the square root into its prime factors and then pair the factors to simplify the expression.
- Product Rule for Radicals: Apply the product rule, which states that the square root of a product is equal to the product of the square roots of each factor.
- Quotient Rule for Radicals: Utilize the quotient rule, similar to the product rule, where the square root of a quotient is equal to the quotient of the square roots of the numerator and denominator.
Step-by-Step Simplification Process
Follow these steps to simplify non-perfect square roots:
- Identifying Perfect Square Factors: Look for perfect square factors within the number inside the square root.
- Writing as a Product of Radicals: Rewrite the radical as a product of two radicals, separating the perfect square factor from the remaining factor.
- Simplifying the Expression: Simplify the expression by taking the square root of the perfect square factor and multiplying it by the remaining radical.
Examples and Practice Problems
Here are some examples and practice problems to help you master the art of simplifying non-perfect square roots:
- Simplifying Numerical Radicals: Example: Simplify √72 by identifying 36 as the largest perfect square factor.
- Simplifying Algebraic Radicals: Example: Simplify √162a5b4 by separating perfect squares.
- Using the Product Rule: Example: Simplify √12 * √3 by combining them into √36.
- Using the Quotient Rule: Example: Simplify √(50x / 2x) by separating the numerator and denominator.
Common Mistakes to Avoid
When simplifying non-perfect square roots, it's crucial to be mindful of certain common errors that can lead to inaccuracies in your calculations. Here are some mistakes to watch out for:
- Forgetting to simplify all factors: One common mistake is neglecting to simplify every factor within the expression. Each perfect square factor should be identified and extracted to simplify the radical fully.
- Misidentifying perfect square factors: It's essential to accurately identify perfect square factors within the number under the square root. Misidentifying these factors can lead to incorrect simplifications and final results.

Additional Resources
- : This website provides comprehensive explanations and interactive examples to help deepen your understanding of square roots, including how to simplify non-perfect square roots.
- : Khan Academy offers a series of instructional videos and practice exercises on rational exponents and radicals, which are essential for mastering the simplification of non-perfect square roots.
- : This video tutorial walks you through various techniques for simplifying square roots, including methods for dealing with non-perfect square roots.
Hướng dẫn chi tiết về cách rút gọn căn bậc hai của một số không phải là số chính phương. Xem video để hiểu rõ hơn về kỹ thuật này.
Hướng dẫn Cách Rút Gọn Căn Bậc Hai của Một Số Không Phải Là Số Chính Phương
READ MORE:
Hướng dẫn đơn giản hóa căn bậc hai của số không phải số chính phương. Video giúp bạn nắm vững cách thức xử lý các số không phải số chính phương trong toán học.
Cách Đơn Giản Hóa Căn Bậc Hai Của Số Không Phải Số Chính Phương