Topic simplifying negative square roots: Understanding how to simplify negative square roots is essential for mastering complex numbers in mathematics. This guide will walk you through the step-by-step process of simplifying negative square roots, providing clear examples and helpful tips to enhance your learning experience.
Table of Content
- Simplifying Negative Square Roots
- Introduction to Square Roots
- Understanding Negative Square Roots
- The Concept of Imaginary Numbers
- Step-by-Step Simplification Process
- Examples and Practice Problems
- Special Cases and Complex Solutions
- Using Technology to Simplify Radicals
- Common Mistakes to Avoid
- Additional Resources for Practice
- YOUTUBE: Video này hướng dẫn cách đơn giản hóa căn bậc hai âm bằng cách sử dụng số tưởng tượng i. Phù hợp cho những ai muốn hiểu rõ hơn về số học phức.
Simplifying Negative Square Roots
Understanding how to simplify the square root of a negative number involves a fundamental concept in algebra: imaginary numbers. Here, we will break down the steps and provide some examples to help you grasp the process.
Step-by-Step Process
- Identify the negative square root to simplify, such as \( \sqrt{-a} \).
- Express the negative square root in terms of \( i \) (the imaginary unit), where \( i = \sqrt{-1} \).
- Simplify the remaining square root, if possible.
Examples
Here are a few examples to illustrate the process:
| Expression | Simplified Form |
|---|---|
| \(\sqrt{-7}\) | \(i\sqrt{7}\) |
| \(\sqrt{-9}\) | \(3i\) |
| \(\sqrt{-12}\) | \(2i\sqrt{3}\) |
Practice Problems
- Simplify \( \sqrt{-5} \)
Solution: \( i\sqrt{5} \)
- Simplify \( \sqrt{-36} \)
Solution: \( 6i \)
- Simplify \( \sqrt{-48} \)
Solution: \( 4i\sqrt{3} \)
- Simplify \( \sqrt{-50} \)
Solution: \( 5i\sqrt{2} \)
General Formula
The general formula for simplifying the square root of a negative number is:
\[
\sqrt{-a} = i\sqrt{a}
\]
Additional Notes
When working with fractions under a square root, use the quotient property of square roots:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
For example:
- \(\sqrt{\frac{21}{64}} = \frac{\sqrt{21}}{\sqrt{64}} = \frac{\sqrt{21}}{8}\)
- \(\sqrt{\frac{28}{81}} = \frac{2\sqrt{7}}{9}\)

READ MORE:
Introduction to Square Roots
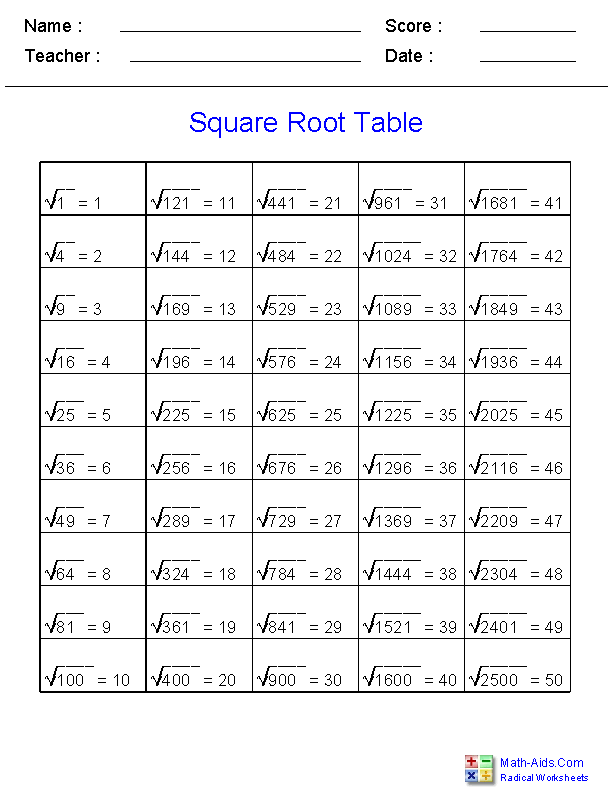
The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). This is represented mathematically as \( \sqrt{x} \). For example, the square root of 9 is 3 because \( 3 \times 3 = 9 \).
Square roots have several important properties and rules:
- Non-negative roots: The square root of a non-negative number is always non-negative. For instance, \( \sqrt{16} = 4 \) and not -4, as we conventionally take the positive root.
- Product Property: The square root of a product is the product of the square roots. Mathematically, \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). For example, \( \sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3} \).
- Quotient Property: The square root of a quotient is the quotient of the square roots. This can be written as \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3} \).
When simplifying square roots, the goal is to make the number inside the square root as small as possible. This process often involves factoring the number into its prime factors and then applying the properties of square roots.
Examples of Simplifying Square Roots
- Simplifying \( \sqrt{18} \):
- Factor 18 into \( 9 \times 2 \).
- Apply the product property: \( \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \cdot \sqrt{2} \).
- Simplify: \( \sqrt{9} = 3 \), so \( \sqrt{18} = 3\sqrt{2} \).
- Simplifying \( \sqrt{50} \):
- Factor 50 into \( 25 \times 2 \).
- Apply the product property: \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \cdot \sqrt{2} \).
- Simplify: \( \sqrt{25} = 5 \), so \( \sqrt{50} = 5\sqrt{2} \).
Understanding these foundational properties and methods of simplification is crucial for tackling more complex mathematical problems, including those involving negative square roots and imaginary numbers.
Understanding Negative Square Roots
When dealing with negative square roots, we venture into the realm of imaginary numbers. Unlike positive square roots, the square root of a negative number does not yield a real number. Instead, it introduces the concept of the imaginary unit, denoted as \( i \), where \( i \) is defined as \( \sqrt{-1} \).
The process of simplifying negative square roots can be broken down into a few steps:
-
Extract the imaginary unit: Rewrite the negative square root as a product of \( \sqrt{-1} \) and the square root of a positive number. For instance:
\[
\sqrt{-a} = \sqrt{-1 \cdot a} = \sqrt{-1} \cdot \sqrt{a} = i\sqrt{a}
\] -
Simplify the positive square root: Simplify the square root of the positive part as you normally would. For example:
\[
\sqrt{-36} = \sqrt{-1 \cdot 36} = \sqrt{-1} \cdot \sqrt{36} = i \cdot 6 = 6i
\]
Let's look at some examples to illustrate this process:
-
Simplify \( \sqrt{-9} \):
\[
\sqrt{-9} = \sqrt{-1 \cdot 9} = \sqrt{-1} \cdot \sqrt{9} = i \cdot 3 = 3i
\] -
Simplify \( \sqrt{-12} \):
\[
\sqrt{-12} = \sqrt{-1 \cdot 12} = \sqrt{-1} \cdot \sqrt{12} = i \cdot \sqrt{4 \cdot 3} = i \cdot 2 \cdot \sqrt{3} = 2i \sqrt{3}
\] -
Simplify \( \sqrt{-50} \):
\[
\sqrt{-50} = \sqrt{-1 \cdot 50} = \sqrt{-1} \cdot \sqrt{50} = i \cdot \sqrt{25 \cdot 2} = i \cdot 5 \cdot \sqrt{2} = 5i \sqrt{2}
\]
These examples demonstrate that simplifying negative square roots primarily involves isolating the imaginary unit and then simplifying the resulting positive square root. Mastering this technique is crucial for solving more complex mathematical problems that involve imaginary numbers.
The Concept of Imaginary Numbers
Imaginary numbers are a class of numbers that extend the real number system. They are defined by the property that the square of an imaginary number is negative. The unit imaginary number is denoted as i, where i is defined as the square root of -1.
In mathematical notation:
This property leads to several important concepts and applications:
- Basic Operations: Imaginary numbers can be added, subtracted, multiplied, and divided just like real numbers, but with special rules for multiplication and division involving i.
- Complex Numbers: Combining real and imaginary numbers forms complex numbers, which are expressed in the form a + bi, where a and b are real numbers.
- Applications: Imaginary and complex numbers are used in various fields such as engineering, physics, and applied mathematics, particularly in the study of oscillations, waves, and electrical circuits.
Here are some basic properties and operations involving imaginary numbers:
| Operation | Result |
|---|---|
Definition of i |
|
i cubed is -i |
|
i to the fourth power is 1 |
When dealing with negative square roots, we use imaginary numbers to express the results. For instance, the square root of -4 can be simplified as follows:
Understanding imaginary numbers allows us to work with and simplify expressions involving negative square roots, making it possible to solve a wider range of mathematical problems.
Step-by-Step Simplification Process
Simplifying negative square roots involves understanding the role of imaginary numbers, particularly the imaginary unit \(i\), which is defined as \(i = \sqrt{-1}\). Here is a detailed step-by-step process:
-
Identify the Negative Square Root:
Recognize that you are dealing with the square root of a negative number, which can be expressed in terms of the imaginary unit \(i\). For example, consider \(\sqrt{-a}\).
-
Factor Out the Negative Sign:
Rewrite the expression by factoring out \(-1\) from the radicand (the number inside the square root). For example:
\[\sqrt{-a} = \sqrt{-1 \cdot a}\]
-
Use the Definition of \(i\):
Substitute \(\sqrt{-1}\) with \(i\). This gives:
\[\sqrt{-a} = \sqrt{-1} \cdot \sqrt{a} = i \cdot \sqrt{a}\]
-
Simplify the Square Root (if possible):
Simplify the remaining square root if \(a\) is a perfect square or can be factored further. Here are a few examples:
-
Example 1: \(\sqrt{-9}\)
\[\sqrt{-9} = \sqrt{-1 \cdot 9} = \sqrt{-1} \cdot \sqrt{9} = i \cdot 3 = 3i\]
-
Example 2: \(\sqrt{-12}\)
\[\sqrt{-12} = \sqrt{-1 \cdot 4 \cdot 3} = \sqrt{-1} \cdot \sqrt{4} \cdot \sqrt{3} = i \cdot 2 \cdot \sqrt{3} = 2i \sqrt{3}\]
-
Example 3: \(\sqrt{-50}\)
\[\sqrt{-50} = \sqrt{-1 \cdot 25 \cdot 2} = \sqrt{-1} \cdot \sqrt{25} \cdot \sqrt{2} = i \cdot 5 \cdot \sqrt{2} = 5i \sqrt{2}\]
-
-
Final Answer:
Combine the simplified terms to get the final result. The final answer should be in the form \(bi\sqrt{c}\), where \(b\) and \(c\) are simplified as much as possible.
This step-by-step process helps ensure that negative square roots are simplified correctly by incorporating the imaginary unit \(i\).
Examples and Practice Problems
Understanding and simplifying negative square roots involves using imaginary numbers. Below are examples and practice problems to help you master this concept.
Example 1
Simplify the square root of -16.
Step-by-Step Solution:
- Identify the negative square root: \( \sqrt{-16} \).
- Rewrite the square root of the negative number using \( i \) (the imaginary unit): \( \sqrt{-16} = \sqrt{16} \cdot \sqrt{-1} \).
- Simplify the square root of 16: \( \sqrt{16} = 4 \).
- Combine the results: \( 4 \cdot \sqrt{-1} = 4i \).
- Thus, \( \sqrt{-16} = 4i \).
Example 2
Simplify the square root of -25.
Step-by-Step Solution:
- Identify the negative square root: \( \sqrt{-25} \).
- Rewrite the square root of the negative number using \( i \): \( \sqrt{-25} = \sqrt{25} \cdot \sqrt{-1} \).
- Simplify the square root of 25: \( \sqrt{25} = 5 \).
- Combine the results: \( 5 \cdot \sqrt{-1} = 5i \).
- Thus, \( \sqrt{-25} = 5i \).
Practice Problems
Try simplifying the following negative square roots:
- \( \sqrt{-9} \)
- \( \sqrt{-36} \)
- \( \sqrt{-49} \)
- \( \sqrt{-64} \)
- \( \sqrt{-81} \)
Solutions to Practice Problems
| Problem | Solution |
|---|---|
| \( \sqrt{-9} \) | \( 3i \) |
| \( \sqrt{-36} \) | \( 6i \) |
| \( \sqrt{-49} \) | \( 7i \) |
| \( \sqrt{-64} \) | \( 8i \) |
| \( \sqrt{-81} \) | \( 9i \) |
With practice, simplifying negative square roots will become an easy task. Remember to always express the negative square root in terms of \( i \) and simplify the positive square root separately.
Special Cases and Complex Solutions
When dealing with negative square roots, special cases and complex solutions often arise. Here, we will explore how to handle these cases and simplify expressions involving imaginary and complex numbers.
Special Cases: Simplifying Negative Square Roots
To simplify the square root of a negative number, we use the imaginary unit \(i\), where \(i = \sqrt{-1}\). Let's look at a few examples:
- Example 1: \(\sqrt{-4}\)
Solution:
\[\sqrt{-4} = \sqrt{-1 \cdot 4} = \sqrt{-1} \cdot \sqrt{4} = i \cdot 2 = 2i\]
- Example 2: \(\sqrt{-18}\)
Solution:
\[\sqrt{-18} = \sqrt{-1 \cdot 18} = \sqrt{-1} \cdot \sqrt{18} = i \cdot \sqrt{18} = i \cdot \sqrt{9 \cdot 2} = 3i\sqrt{2}\]
- Example 3: \(\sqrt{-50}\)
Solution:
\[\sqrt{-50} = \sqrt{-1 \cdot 50} = \sqrt{-1} \cdot \sqrt{50} = i \cdot \sqrt{50} = i \cdot \sqrt{25 \cdot 2} = 5i\sqrt{2}\]
Complex Solutions to Quadratic Equations
When solving quadratic equations, we may encounter complex solutions. A quadratic equation of the form \(ax^2 + bx + c = 0\) can have complex solutions if the discriminant (\(b^2 - 4ac\)) is negative.
- Example 4: Solve \(x^2 + 4x + 5 = 0\)
Solution:
- Calculate the discriminant: \(b^2 - 4ac = 4^2 - 4 \cdot 1 \cdot 5 = 16 - 20 = -4\)
- Since the discriminant is negative, the solutions are complex:
- \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-4 \pm \sqrt{-4}}{2 \cdot 1} = \frac{-4 \pm 2i}{2} = -2 \pm i\]
- Example 5: Solve \(x^2 - 6x + 13 = 0\)
Solution:
- Calculate the discriminant: \(b^2 - 4ac = (-6)^2 - 4 \cdot 1 \cdot 13 = 36 - 52 = -16\)
- Since the discriminant is negative, the solutions are complex:
- \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-(-6) \pm \sqrt{-16}}{2 \cdot 1} = \frac{6 \pm 4i}{2} = 3 \pm 2i\]
Properties of Complex Numbers
A complex number is expressed as \(a + bi\), where \(a\) is the real part and \(b\) is the imaginary part.
- Addition: To add two complex numbers, add their real parts and their imaginary parts separately.
\[(3 + 4i) + (1 + 2i) = (3 + 1) + (4i + 2i) = 4 + 6i\]
- Subtraction: To subtract two complex numbers, subtract their real parts and their imaginary parts separately.
\[(3 + 4i) - (1 + 2i) = (3 - 1) + (4i - 2i) = 2 + 2i\]
- Multiplication: To multiply two complex numbers, use the distributive property and remember that \(i^2 = -1\).
\[(3 + 4i)(1 + 2i) = 3 \cdot 1 + 3 \cdot 2i + 4i \cdot 1 + 4i \cdot 2i = 3 + 6i + 4i + 8i^2 = 3 + 10i + 8(-1) = -5 + 10i\]
Using Technology to Simplify Radicals
Technology can significantly simplify the process of working with radicals, including negative square roots. Several tools and software are available that can help you perform these calculations quickly and accurately. Below are some methods and step-by-step instructions on how to use these technologies:
-
Graphing Calculators:
Modern graphing calculators, such as the TI-84 or Casio models, have functions specifically designed for simplifying radicals.
- Turn on the calculator and access the math functions menu.
- Enter the radical expression using the square root function (usually labeled as
√orsqrt()). - For negative square roots, ensure you use the imaginary unit
iwhere necessary (e.g.,sqrt(-4) = 2i). - Press enter to see the simplified result.
-
Online Calculators:
Many websites offer free tools to simplify radicals. These are particularly useful for quick calculations and checking work.
- Open a web browser and navigate to a trusted online calculator, such as WolframAlpha or Symbolab.
- Input the radical expression directly into the search or calculation bar.
- Include the imaginary unit
ifor negative square roots (e.g.,sqrt(-9)). - Press the calculate button to get the simplified result instantly.
-
Math Software:
Software such as Mathematica, MATLAB, and Maple offer advanced features for working with radicals and complex numbers.
- Install and open the software on your computer.
- Use the built-in functions for square roots and imaginary numbers (e.g., in MATLAB, use
sqrt(-x)). - Input your expression and execute the command to receive the simplified form.
-
Mobile Apps:
Many educational apps available for smartphones and tablets can simplify radicals. Apps like Photomath and Microsoft Math Solver are popular choices.
- Download and install the app from your device's app store.
- Open the app and select the appropriate function for simplifying radicals.
- Use the camera feature to scan the expression or manually input it.
- The app will process the expression and provide the simplified result.
By leveraging these technological tools, you can streamline the process of simplifying radicals, making your work more efficient and accurate.
Common Mistakes to Avoid
When simplifying negative square roots and working with complex numbers, it's essential to avoid common mistakes that can lead to incorrect results. Below are some frequent errors and tips on how to avoid them:
- Ignoring the Imaginary Unit \(i\):
When dealing with the square root of a negative number, always include the imaginary unit \(i\). For example, \(\sqrt{-4} = 2i\), not just 2 or \(-2\).
- Incorrect Application of Square Root Properties:
The property \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) holds only if both \(a\) and \(b\) are nonnegative. For example, \(\sqrt{-4 \cdot -9} \neq \sqrt{-4} \cdot \sqrt{-9}\). Instead, \(\sqrt{36} = 6\).
- Misunderstanding Principal and Negative Roots:
Remember that \(\sqrt{a^2} = |a|\). For instance, \(\sqrt{(-5)^2} = 5\), not \(-5\). This ensures that you always take the principal (nonnegative) root.
- Incorrectly Simplifying Complex Expressions:
When simplifying expressions like \(\sqrt{-a \cdot -b}\), break them down properly: \(\sqrt{-a \cdot -b} = \sqrt{a \cdot b} \cdot i^2 = \sqrt{a \cdot b} \cdot (-1)\).
- Forgetting to Simplify Radicals Fully:
Always simplify radicals as much as possible. For example, simplify \(\sqrt{50}\) to \(5\sqrt{2}\), and \(\sqrt{-50}\) to \(5i\sqrt{2}\).
- Incorrectly Factoring Expressions:
Ensure correct factoring before applying square root properties. For instance, \(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\) and not \(\sqrt{25 + 2}\).
- Misinterpreting Square Root Operations:
Be cautious with operations involving square roots. For example, \(\sqrt{a^2 + b^2} \neq a + b\). Simplify within the radical first.
- Not Using Absolute Values When Necessary:
For expressions involving variables, use absolute values to ensure nonnegative results. For example, \(\sqrt{x^2} = |x|\).
By being aware of these common mistakes and applying the correct methods, you can avoid errors and ensure accurate simplification of negative square roots and complex numbers.

Additional Resources for Practice
Practicing the simplification of negative square roots is essential for mastering the concept. Below are some useful resources that provide detailed explanations, practice problems, and interactive tools:
-
This resource includes instructional videos and practice problems to help you understand and simplify square roots involving negative numbers. The interactive format allows you to test your understanding and get immediate feedback.
-
This comprehensive guide covers the basics of square roots, including the principal square root and the square roots of negative numbers. It includes worked examples and exercises to reinforce your learning.
-
Study.com provides a series of lessons and quizzes on simplifying square roots. The platform's structured approach helps you grasp the fundamental concepts and apply them to various problems.
-
Quizlet offers flashcards and practice sets that cover the simplification of square roots, including those with negative radicands. This resource is great for quick revision and self-testing.
-
Symbolab's online calculator helps you simplify square roots step-by-step. It is a useful tool for checking your work and understanding the process of simplification in detail.
These resources offer a variety of approaches and tools to help you practice and master the simplification of negative square roots. Utilize them to reinforce your learning and gain confidence in handling complex mathematical problems.
Video này hướng dẫn cách đơn giản hóa căn bậc hai âm bằng cách sử dụng số tưởng tượng i. Phù hợp cho những ai muốn hiểu rõ hơn về số học phức.
Đơn Giản Hóa Căn Bậc Hai Âm Sử Dụng Số Tưởng Tượng i
READ MORE:
Video này hướng dẫn cách đơn giản hóa các căn bậc hai âm. Phù hợp cho những ai muốn hiểu rõ hơn về việc đơn giản hóa căn bậc hai âm.
Đơn Giản Hóa Căn Bậc Hai Âm