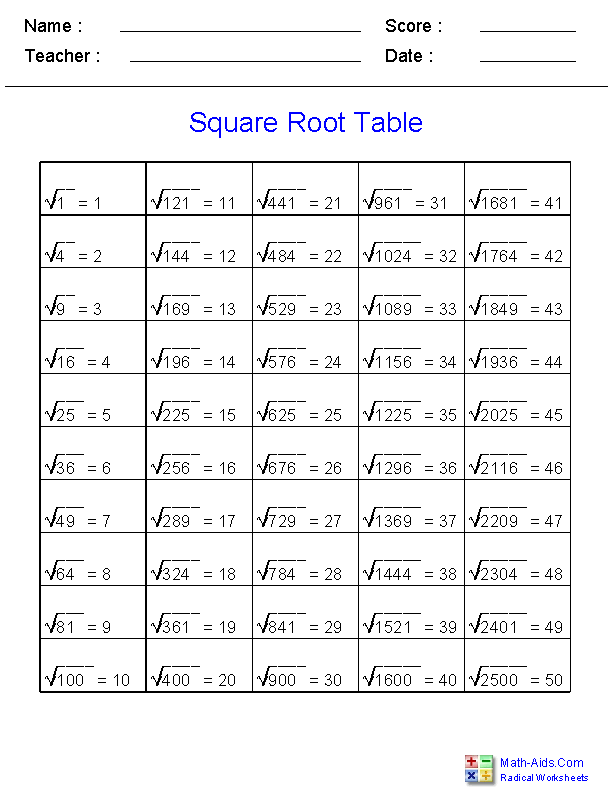
Topic how to solve square roots without a calculator: Discover effective and easy methods to solve square roots without using a calculator. This guide will provide you with step-by-step techniques and helpful tips to master square roots, enabling you to tackle math problems with confidence and ease. Enhance your mathematical skills and learn to solve square roots effortlessly.
Table of Content
- How to Solve Square Roots Without a Calculator
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Basic Properties of Square Roots
- Methods to Simplify Square Roots
- Prime Factorization Method
- Using the Estimation Method
- Long Division Method for Square Roots
- Solving Square Roots of Perfect Squares
- Handling Non-Perfect Squares
- Square Roots in Mathematical Expressions
- Common Mistakes to Avoid
- Practice Problems and Solutions
- Conclusion and Tips for Mastery
- YOUTUBE:
How to Solve Square Roots Without a Calculator
Finding square roots without a calculator can be accomplished using several methods. This guide will provide step-by-step instructions on prime factorization, the long division method, and estimation strategies.
1. Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5, because 5 x 5 = 25. The symbol for square root is '√', and the number under the square root symbol is called the radicand.
2. Prime Factorization Method
This method involves breaking down the number into its prime factors and then pairing them.
- Find the prime factors of the number.
- Pair up identical factors.
- Take one factor from each pair and multiply them.
For example, to find the square root of 400:
- Prime factors: 400 = 2 x 2 x 2 x 2 x 5 x 5
- Pairing the factors: (2 x 2), (2 x 2), (5 x 5)
- Taking one factor from each pair: 2 x 2 x 5 = 20
- Therefore, √400 = 20
3. Long Division Method
This method is especially useful for larger numbers and provides a systematic way to find the square root.
- Start by grouping the digits of the number in pairs from right to left.
- Estimate the largest number whose square is less than or equal to the first group.
- Subtract the square of this number from the first group and bring down the next pair of digits.
- Double the quotient and determine the next digit of the root through estimation and division.
- Repeat the process until all pairs have been used.
4. Estimation Strategy
Estimation helps to quickly find an approximate square root.
- Identify two perfect squares between which the number lies.
- Estimate a value between these two numbers.
- For example, for √40, since 36 (6²) and 49 (7²) are the closest perfect squares, the square root of 40 is between 6 and 7.
- Refine the estimate by averaging and adjusting based on the distance from the perfect squares.
For √40:
- Estimate: (49 - 40) / (2 x 6) = 9 / 12 ≈ 0.75
- Approximate root: 6 + 0.75 = 6.75
5. Tips and Tricks
- Practice simplifying square roots using prime factorization for quick mental calculations.
- For large numbers, use the long division method to get accurate results.
- Estimation is useful for quick approximations and is often sufficient for practical purposes.
6. Practice Exercises
Try finding the square roots of the following numbers without using a calculator:
- √81
- √144
- √225
- √361
Check your answers using the methods described above.
Conclusion
Mastering the art of finding square roots without a calculator not only enhances your mathematical skills but also boosts your confidence in tackling various numerical problems. Embrace these methods and enjoy the process of learning and applying mathematical concepts in everyday life.

READ MORE:
Introduction to Square Roots
Square roots are mathematical functions that return a number which, when multiplied by itself, gives the original number. Understanding square roots is essential for solving various mathematical problems. This section will provide an overview of square roots, including their properties and basic concepts.
Here are some key points to understand about square roots:
- The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \).
- Square roots are often denoted using the radical symbol \( \sqrt{} \).
- Every positive number has two square roots: a positive root and a negative root. For example, \( \sqrt{9} = 3 \) and \( \sqrt{9} = -3 \).
- The square root of zero is zero: \( \sqrt{0} = 0 \).
- Negative numbers do not have real square roots, but they have complex square roots.
To better understand square roots, consider the following table of perfect squares and their square roots:
| Number | Square | Square Root |
|---|---|---|
| 1 | 1 | 1 |
| 4 | 16 | 2 |
| 9 | 81 | 3 |
| 16 | 256 | 4 |
| 25 | 625 | 5 |
Understanding these basic principles will help you tackle more complex problems involving square roots. In the following sections, we will explore different methods to solve square roots without using a calculator, ensuring you have a strong foundation in this fundamental mathematical concept.
Understanding the Concept of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. This fundamental mathematical concept is crucial for solving various types of problems. To understand square roots better, let's delve into their properties, notation, and examples.
Here are some key points to consider:
- The square root of a number \( x \) is denoted as \( \sqrt{x} \).
- Square roots can be positive or negative because both \( 3^2 = 9 \) and \( (-3)^2 = 9 \). Hence, \( \sqrt{9} = 3 \) and \( \sqrt{9} = -3 \).
- For any non-negative number \( x \), \( \sqrt{x} \) represents the principal (non-negative) square root.
- Negative numbers do not have real square roots since no real number squared equals a negative number. They have complex square roots instead.
To illustrate, consider the following steps and examples:
- Identify the number: Determine the number for which you want to find the square root. For example, let's find the square root of 25.
- Perfect squares: Check if the number is a perfect square (a number that is the square of an integer). Here, 25 is a perfect square since \( 5 \times 5 = 25 \). Therefore, \( \sqrt{25} = 5 \).
- Non-perfect squares: For numbers that are not perfect squares, estimate between which two perfect squares the number lies. For example, for \( \sqrt{20} \), since \( 16 < 20 < 25 \), \( \sqrt{20} \) is between 4 and 5.
- Refine the estimate: Use methods like prime factorization, long division, or approximation to get a more accurate value.
Let's summarize the relationship between some numbers and their square roots:
| Number | Square Root |
|---|---|
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
Understanding these basics of square roots is vital for solving more complex mathematical problems without a calculator. The upcoming sections will guide you through different methods to solve square roots manually, enhancing your mathematical proficiency.
Basic Properties of Square Roots
Understanding the basic properties of square roots is essential for solving them without a calculator. These properties help simplify expressions and solve equations involving square roots. Here are the fundamental properties you need to know:
- Non-negativity: The square root of a non-negative number is always non-negative. For any \( x \geq 0 \), \( \sqrt{x} \geq 0 \).
- Product Property: The square root of a product is the product of the square roots of the factors. Mathematically, \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \) for any non-negative numbers \( a \) and \( b \).
- Quotient Property: The square root of a quotient is the quotient of the square roots. For any non-negative numbers \( a \) and \( b \) (where \( b \neq 0 \)), \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Power Property: The square root can be expressed as a power. For any non-negative number \( x \), \( \sqrt{x} = x^{1/2} \).
- Square of a Square Root: The square of the square root of a number returns the original number. \( (\sqrt{x})^2 = x \) for any \( x \geq 0 \).
- Addition and Subtraction: The square root of a sum or difference is not the sum or difference of the square roots. That is, \( \sqrt{a+b} \neq \sqrt{a} + \sqrt{b} \) and \( \sqrt{a-b} \neq \sqrt{a} - \sqrt{b} \).
Here are some examples to illustrate these properties:
| Property | Example | Explanation |
|---|---|---|
| Product Property | \( \sqrt{36 \times 25} = \sqrt{36} \times \sqrt{25} = 6 \times 5 = 30 \) | Square root of product equals product of square roots |
| Quotient Property | \( \sqrt{\frac{49}{9}} = \frac{\sqrt{49}}{\sqrt{9}} = \frac{7}{3} \) | Square root of quotient equals quotient of square roots |
| Power Property | \( \sqrt{16} = 16^{1/2} = 4 \) | Square root expressed as a power |
| Square of a Square Root | \( (\sqrt{25})^2 = 25 \) | Square of square root returns original number |
These basic properties form the foundation for solving square roots without a calculator. By applying these principles, you can simplify complex expressions and solve square root problems more efficiently.
Methods to Simplify Square Roots
Simplifying square roots involves reducing the expression under the square root to its simplest form. There are several methods to achieve this, each useful in different scenarios. Below are the most effective methods to simplify square roots step by step:
1. Prime Factorization Method
This method involves breaking down the number into its prime factors and then simplifying.
- Factorize the number: Write the number as a product of its prime factors.
- Group the factors: Pair the prime factors.
- Simplify: Take one number from each pair out of the square root.
Example:
- \(\sqrt{72}\)
- Prime factorization of 72: \(72 = 2^3 \times 3^2\)
- Grouping factors: \(\sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 3^2) \times 2} = \sqrt{(2 \times 3)^2 \times 2}\)
- Simplify: \(6\sqrt{2}\)
2. Simplifying Fractions
This method involves simplifying square roots within a fraction.
- Simplify the fraction: Reduce the fraction to its simplest form.
- Apply the square root: Take the square root of the numerator and the denominator separately.
Example:
- \(\sqrt{\frac{50}{8}}\)
- Simplify the fraction: \(\frac{50}{8} = \frac{25}{4}\)
- Apply the square root: \(\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2}\)
3. Using the Product Property
This method uses the property \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\) to simplify the square root.
- Identify factors: Find factors of the number that are perfect squares.
- Separate the factors: Write the square root as the product of two square roots.
- Simplify: Simplify the square roots individually.
Example:
- \(\sqrt{48}\)
- Identify factors: \(48 = 16 \times 3\)
- Separate the factors: \(\sqrt{48} = \sqrt{16 \times 3} = \sqrt{16} \times \sqrt{3}\)
- Simplify: \(4\sqrt{3}\)
4. Estimation Method
This method is useful when an exact simplification isn't possible, and an approximate value is acceptable.
- Identify nearby perfect squares: Determine the perfect squares between which the number lies.
- Estimate the value: Use the values of the perfect squares to estimate the square root.
Example:
- \(\sqrt{50}\)
- Identify nearby perfect squares: \(49 < 50 < 64\)
- Estimate the value: \(7 < \sqrt{50} < 8\). Since 50 is closer to 49, \(\sqrt{50} \approx 7.1\)
These methods provide a structured approach to simplify square roots without a calculator. By mastering these techniques, you can tackle a wide range of square root problems effectively.

Prime Factorization Method
The Prime Factorization Method is an effective way to simplify square roots by breaking down the number into its prime factors. This method works particularly well for simplifying square roots of larger numbers. Follow these steps to use the Prime Factorization Method:
- Factorize the number: Begin by expressing the number as a product of its prime factors.
- Group the factors: Pair the prime factors to form squares.
- Simplify the square root: Take one number from each pair out of the square root.
Let's look at a detailed example to illustrate this method:
- Example: Simplify \( \sqrt{72} \)
- Step 1: Factorize the number: Find the prime factors of 72.
- 72 can be divided by 2: \( 72 = 2 \times 36 \)
- 36 can be divided by 2: \( 36 = 2 \times 18 \)
- 18 can be divided by 2: \( 18 = 2 \times 9 \)
- 9 can be divided by 3: \( 9 = 3 \times 3 \)
- So, \( 72 = 2^3 \times 3^2 \)
- Step 2: Group the factors: Pair the prime factors.
- \( 72 = 2^3 \times 3^2 \)
- Group into pairs: \( 2^3 = 2 \times 2 \times 2 \) and \( 3^2 = 3 \times 3 \)
- So, \( 72 = (2^2 \times 3^2) \times 2 = (2 \times 3)^2 \times 2 \)
- Step 3: Simplify the square root: Take one number from each pair out of the square root.
- \( \sqrt{72} = \sqrt{(2 \times 3)^2 \times 2} \)
- Take the square root of the perfect square: \( (2 \times 3) \)
- \( \sqrt{72} = 6\sqrt{2} \)
Another example:
- Example: Simplify \( \sqrt{180} \)
- Step 1: Factorize the number: Find the prime factors of 180.
- 180 can be divided by 2: \( 180 = 2 \times 90 \)
- 90 can be divided by 2: \( 90 = 2 \times 45 \)
- 45 can be divided by 3: \( 45 = 3 \times 15 \)
- 15 can be divided by 3: \( 15 = 3 \times 5 \)
- So, \( 180 = 2^2 \times 3^2 \times 5 \)
- Step 2: Group the factors: Pair the prime factors.
- \( 180 = 2^2 \times 3^2 \times 5 \)
- Group into pairs: \( 2^2 = 2 \times 2 \) and \( 3^2 = 3 \times 3 \)
- So, \( 180 = (2^2 \times 3^2) \times 5 = (2 \times 3)^2 \times 5 \)
- Step 3: Simplify the square root: Take one number from each pair out of the square root.
- \( \sqrt{180} = \sqrt{(2 \times 3)^2 \times 5} \)
- Take the square root of the perfect square: \( (2 \times 3) \)
- \( \sqrt{180} = 6\sqrt{5} \)
By following these steps, you can simplify square roots using the Prime Factorization Method effectively.
Using the Estimation Method
The Estimation Method is a useful technique to approximate the square root of a number without a calculator. This method involves identifying the nearest perfect squares and refining your estimate based on their proximity to the target number. Follow these steps to use the Estimation Method:
- Identify the perfect squares: Find the perfect squares that are closest to the given number.
- Determine the range: Establish the range within which the square root lies, based on the perfect squares.
- Estimate the square root: Refine the estimate by considering the proximity of the given number to the nearest perfect squares.
Let's look at detailed examples to illustrate this method:
- Example: Estimate \( \sqrt{50} \)
- Step 1: Identify the perfect squares:
- The nearest perfect squares to 50 are 49 and 64.
- Step 2: Determine the range:
- \( \sqrt{49} = 7 \) and \( \sqrt{64} = 8 \)
- So, \( 7 < \sqrt{50} < 8 \)
- Step 3: Estimate the square root:
- Since 50 is closer to 49 than to 64, \( \sqrt{50} \) is slightly more than 7.
- We can approximate: \( \sqrt{50} \approx 7.1 \)
Another example:
- Example: Estimate \( \sqrt{75} \)
- Step 1: Identify the perfect squares:
- The nearest perfect squares to 75 are 64 and 81.
- Step 2: Determine the range:
- \( \sqrt{64} = 8 \) and \( \sqrt{81} = 9 \)
- So, \( 8 < \sqrt{75} < 9 \)
- Step 3: Estimate the square root:
- Since 75 is closer to 81 than to 64, \( \sqrt{75} \) is slightly less than 9.
- We can approximate: \( \sqrt{75} \approx 8.7 \)
These examples show how the Estimation Method can provide a close approximation of square roots. With practice, this method allows you to quickly estimate square roots mentally or on paper.
Long Division Method for Square Roots
The Long Division Method is a systematic technique to find the square root of a number without a calculator. This method involves dividing the number into pairs of digits and estimating the square root step by step. Here is a detailed guide on how to use the Long Division Method:
- Set up the number: Divide the number into pairs of digits, starting from the decimal point. If the number has an odd number of digits, the first digit will be a single digit.
- Find the largest square: Determine the largest square less than or equal to the first pair or single digit. Write this number as the first digit of the square root.
- Subtract and bring down: Subtract the square from the first pair or single digit and bring down the next pair of digits.
- Double and estimate: Double the current result of the square root and write it as a divisor. Estimate how many times the divisor can fit into the new dividend.
- Repeat: Subtract the product of the divisor and the estimate from the current dividend, bring down the next pair of digits, and repeat the process until you reach the desired precision.
Let's look at an example to illustrate this method:
- Example: Find the square root of 529
- Step 1: Set up the number:
- 529 is divided into pairs: 5 | 29
- Step 2: Find the largest square:
- The largest square less than or equal to 5 is 2 (since \(2^2 = 4\)).
- Write 2 as the first digit of the square root.
- Step 3: Subtract and bring down:
- Subtract \(4\) from \(5\): \(5 - 4 = 1\).
- Bring down the next pair (29), making the new dividend 129.
- Step 4: Double and estimate:
- Double the current result (2): \(2 \times 2 = 4\).
- Estimate how many times 40 can fit into 129. The answer is 3 (since \(43 \times 3 = 129\)).
- Write 3 as the next digit of the square root.
- Step 5: Repeat:
- Subtract \(129\) from \(129\): \(129 - 129 = 0\).
- There are no more digits to bring down, so the process is complete.
The square root of 529 is 23.
Another example:
- Example: Find the square root of 2.25
- Step 1: Set up the number:
- 2.25 is divided into pairs: 2 | 25
- Step 2: Find the largest square:
- The largest square less than or equal to 2 is 1 (since \(1^2 = 1\)).
- Write 1 as the first digit of the square root.
- Step 3: Subtract and bring down:
- Subtract \(1\) from \(2\): \(2 - 1 = 1\).
- Bring down the next pair (25), making the new dividend 125.
- Step 4: Double and estimate:
- Double the current result (1): \(1 \times 2 = 2\).
- Estimate how many times 20 can fit into 125. The answer is 6 (since \(26 \times 6 = 156\), but we use 5 since \(25 \times 5 = 125\)).
- Write 5 as the next digit of the square root.
- Step 5: Repeat:
- Subtract \(125\) from \(125\): \(125 - 125 = 0\).
- There are no more digits to bring down, so the process is complete.
The square root of 2.25 is 1.5.
By following these steps, you can accurately find the square root of any number using the Long Division Method.
Solving Square Roots of Perfect Squares
Solving the square roots of perfect squares is straightforward and involves recognizing the number that, when multiplied by itself, gives the original number. Here are the steps to solve the square roots of perfect squares:
- Identify the perfect square: Check if the number is a perfect square by finding its factors and verifying if one factor is repeated twice.
- Find the square root: Determine the number that, when multiplied by itself, equals the perfect square.
Let's look at detailed examples to illustrate this method:
- Example: Find the square root of 144
- Step 1: Identify the perfect square:
- 144 can be factorized as \( 12 \times 12 \).
- Since \( 12 \times 12 = 144 \), 144 is a perfect square.
- Step 2: Find the square root:
- The square root of 144 is 12.
Another example:
- Example: Find the square root of 81
- Step 1: Identify the perfect square:
- 81 can be factorized as \( 9 \times 9 \).
- Since \( 9 \times 9 = 81 \), 81 is a perfect square.
- Step 2: Find the square root:
- The square root of 81 is 9.
Another example:
- Example: Find the square root of 225
- Step 1: Identify the perfect square:
- 225 can be factorized as \( 15 \times 15 \).
- Since \( 15 \times 15 = 225 \), 225 is a perfect square.
- Step 2: Find the square root:
- The square root of 225 is 15.
By following these simple steps, you can easily solve the square roots of perfect squares.

Handling Non-Perfect Squares
Finding the square root of non-perfect squares can be more challenging, but there are several methods that can help you approximate or simplify these roots. Here are some effective techniques:
Estimation Method
The estimation method involves finding two perfect squares between which your number lies and then estimating the square root. Follow these steps:
- Identify the perfect squares closest to the number. For example, for \( \sqrt{20} \), the closest perfect squares are 16 (\(4^2\)) and 25 (\(5^2\)).
- Estimate the square root as a value between these two numbers. For \( \sqrt{20} \), it lies between 4 and 5.
- Refine the estimate by choosing a number between 4 and 5 and squaring it. For example, \(4.5^2 = 20.25\), which is close to 20.
- Adjust your estimate up or down based on the result. Here, you might try a number slightly lower than 4.5, such as 4.47, to get a closer approximation.
Prime Factorization Method
Another approach is to use prime factorization to simplify the square root:
- Factorize the number into its prime factors. For example, 45 can be factorized into \( 45 = 3 \times 3 \times 5 \).
- Pair the prime factors. Each pair of the same number can be taken out of the square root. For \( \sqrt{45} = \sqrt{3 \times 3 \times 5} = 3\sqrt{5} \).
Long Division Method
The long division method is a more precise way to find square roots without a calculator. Here’s how it works:
- Group the digits of the number in pairs starting from the decimal point. For example, for 20, it becomes (20.00).
- Find the largest number whose square is less than or equal to the first group. Subtract its square from the first group and bring down the next pair of digits. For example, 4 is the largest number whose square (16) is less than 20, so write down 4 and subtract 16 from 20 to get 4.
- Double the quotient (4) and write it down with a blank next to it (8_). Find a digit to fill in the blank such that when the number formed is multiplied by the same digit, the product is less than or equal to the current dividend (400). In this case, 8 fits, as \(48 \times 8 = 384\). Subtract to get 16.
- Repeat the process with the next pair of digits (1600), doubling the quotient (48) to 96_. Find the next digit, which is 1, to get \(961 \times 1 = 961\). Subtract to get 639.
- Continue this process to find more decimal places of the square root as needed.
Example Calculation
Let's calculate \( \sqrt{20} \) using the long division method:
| Step | Operation | Result |
| 1 | Find largest square less than 20 | 4 (since \( 4^2 = 16 \)) |
| 2 | Subtract 16 from 20 | 4 |
| 3 | Bring down next pair (00) | 400 |
| 4 | Double quotient (4 to 8_) | 8_ |
| 5 | Find suitable digit (8 to form 88) | 48 \times 8 = 384 |
| 6 | Subtract 384 from 400 | 16 |
| 7 | Bring down next pair (00) | 1600 |
| 8 | Double quotient (48 to 96_) | 96_ |
| 9 | Find suitable digit (1 to form 961) | 961 \times 1 = 961 |
Conclusion
By using these methods, you can effectively find the square root of non-perfect squares. Practice these techniques to become more comfortable with handling non-perfect squares without a calculator.
Square Roots in Mathematical Expressions
Square roots frequently appear in various mathematical expressions, and understanding how to manipulate these expressions is crucial. This section will guide you through different scenarios where square roots are involved and how to handle them.
1. Adding and Subtracting Square Roots
When adding or subtracting square roots, the key is to simplify them as much as possible first. Only like square roots can be combined.
- \(\sqrt{a} + \sqrt{b}\) cannot be simplified unless \(a = b\).
- \(\sqrt{a} + \sqrt{a} = 2\sqrt{a}\).
For example:
2. Multiplying Square Roots
Multiplying square roots is straightforward: multiply the numbers inside the radicals and then simplify if possible.
For example:
3. Dividing Square Roots
Dividing square roots involves placing them under a single radical and then simplifying.
For example:
4. Rationalizing Denominators
When a square root appears in the denominator of a fraction, rationalize the denominator by multiplying both the numerator and the denominator by the square root in the denominator.
For example:
5. Solving Equations with Square Roots
To solve equations involving square roots, isolate the square root on one side and then square both sides of the equation to eliminate the square root. Ensure to check for extraneous solutions.
For example:
Check the solution:
Understanding how to manipulate square roots in mathematical expressions is essential for solving complex problems. Practice these techniques regularly to gain proficiency.
Common Mistakes to Avoid
When solving square roots without a calculator, it's easy to make errors that can lead to incorrect results. Here are some common mistakes to watch out for and tips on how to avoid them:
- Forgetting to Simplify: Always simplify the square root as much as possible. For instance, \( \sqrt{50} \) can be simplified to \( 5\sqrt{2} \) by recognizing that \( 50 = 25 \times 2 \) and \( \sqrt{25} = 5 \).
- Ignoring Negative Roots: Remember that every positive number has both a positive and negative square root. While \( \sqrt{16} \) is 4, it is also -4.
- Mistakes in Prime Factorization: Ensure that all factors are correctly paired. For example, when breaking down \( \sqrt{72} \):
- Prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Paired factors: \( (2 \times 2) \times (3 \times 3) \)
- Simplified: \( 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \)
- Errors in Estimation: When estimating square roots, ensure you are using the correct reference points. For example, to estimate \( \sqrt{45} \):
- Identify closest perfect squares: 36 (\(6^2\)) and 49 (\(7^2\))
- Since 45 is closer to 49, estimate \( \sqrt{45} \approx 6.7 \)
- Misapplication of Methods: Each method (estimation, prime factorization, long division) has its place. Use prime factorization for simpler, smaller numbers and long division for larger, more complex numbers.
- Inaccurate Division in Long Division Method: Ensure that each step of the long division is precise:
- Separate the number into pairs from the decimal point.
- Find the largest number whose square is less than or equal to the first pair.
- Subtract and bring down the next pair, continuing the process accurately.
By being mindful of these common mistakes and following systematic methods, you can accurately find square roots without a calculator.
Practice Problems and Solutions
Here are some practice problems with detailed solutions to help you master finding square roots without a calculator:
-
Find the square root of 144
- Recognize that 144 is a perfect square.
- Find the prime factorization: \( 144 = 2^4 \times 3^2 \).
- Pair the factors: \( \sqrt{144} = \sqrt{(2^2)^2 \times 3^2} \).
- Simplify by taking one number from each pair: \( \sqrt{144} = 2^2 \times 3 = 12 \).
So, \( \sqrt{144} = 12 \).
-
Find the square root of 50 using prime factorization
- Find the prime factors: \( 50 = 2 \times 5^2 \).
- Pair the factors: \( \sqrt{50} = \sqrt{2 \times 5^2} \).
- Simplify: \( \sqrt{50} = 5\sqrt{2} \).
So, \( \sqrt{50} = 5\sqrt{2} \).
-
Estimate the square root of 45 using the approximation method
- Identify the closest perfect squares: \( 36 \) (which is \( 6^2 \)) and \( 49 \) (which is \( 7^2 \)).
- Since 45 is closer to 49, estimate between 6 and 7.
- Use average: \( 6.5^2 = 42.25 \) (too low) and \( 6.6^2 = 43.56 \) (still low).
- Try \( 6.7^2 = 44.89 \) (very close).
So, \( \sqrt{45} \approx 6.7 \).
-
Find the square root of 20 using the long division method
- Pair digits from the decimal point: \( 20.00 \).
- Find the largest number whose square is less than or equal to 20: \( 4^2 = 16 \).
- Subtract: \( 20 - 16 = 4 \). Bring down 00: \( 400 \).
- Double the quotient (4) and find the next digit: \( 8 \times 5 = 40 \), so 45 is the divisor.
- Divide: \( 400 \div 45 \approx 8 \).
So, \( \sqrt{20} \approx 4.47 \).

Conclusion and Tips for Mastery
Mastering the skill of solving square roots without a calculator is a valuable mathematical endeavor. Not only does it enhance your numerical agility, but it also builds confidence in handling complex problems. Here are some key takeaways and tips for mastery:
- Understand the Basics: Begin with a clear understanding of what a square root is. The square root of a number \(x\) is a value \(y\) such that \(y^2 = x\).
- Learn Different Methods: Familiarize yourself with various methods such as prime factorization, the long division method, and estimation techniques.
- Practice Regularly: Consistent practice is crucial. Work on a variety of problems, both perfect squares and non-perfect squares, to build proficiency.
- Double-Check Your Work: Always verify your results by squaring your answer to see if it matches the original number.
- Use Estimation for Quick Checks: Develop the skill of estimating square roots for quicker approximations, especially useful for non-perfect squares.
- Break Down Complex Problems: For large numbers, break them down into smaller factors and handle them step by step using the methods you’ve learned.
- Avoid Common Mistakes: Be aware of common errors such as misplacing decimal points or incorrect factor pairing. Ensure each step is carefully executed.
By following these tips and continuously challenging yourself with new problems, you can achieve mastery in calculating square roots manually. This not only strengthens your mathematical foundation but also enhances your problem-solving skills across various applications.
Xấp Xỉ Căn Bậc Hai Mà Không Cần Máy Tính
READ MORE:
Tìm Căn Bậc Hai Bằng Tay Mà Không Cần Máy Tính