Topic how to simplifying square roots: Learn how to simplify square roots with our comprehensive guide! Simplifying square roots can be straightforward and fun when you understand the process. Whether you're a student or just looking to brush up on your math skills, our step-by-step instructions and examples will help you master this essential mathematical technique with ease.
Table of Content
- How to Simplify Square Roots
- Introduction to Simplifying Square Roots
- Understanding Square Roots
- Basic Concepts of Simplifying Square Roots
- Prime Factorization Method
- Step-by-Step Guide to Simplifying Square Roots
- Examples of Simplifying Square Roots
- Common Mistakes and How to Avoid Them
- Practice Problems for Simplifying Square Roots
- Advanced Techniques for Simplifying Square Roots
- Applications of Simplified Square Roots in Real Life
- Additional Resources and Practice Worksheets
- Conclusion and Summary
- YOUTUBE: Hướng dẫn Cách Đơn Giản Hóa Căn Bậc Hai
How to Simplify Square Roots
Simplifying square roots involves reducing the expression to its simplest form. Here, we outline a step-by-step method to simplify square roots, which is helpful for students learning basic algebra.
Step-by-Step Method
- Find the prime factors of the number under the square root.
- Pair the prime factors.
- Move each pair of prime factors outside the square root.
- Multiply the numbers outside the square root together.
- Multiply the remaining numbers inside the square root together.
Example
Simplify \( \sqrt{72} \):
- Prime factorization of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Pair the prime factors: \( (2 \times 2), (3 \times 3) \)
- Move pairs outside the square root: \( 2 \times 3 \)
- Remaining inside the square root: \( \sqrt{2} \)
- Simplified form: \( 6\sqrt{2} \)
Practice Problems
- Simplify \( \sqrt{50} \)
- Simplify \( \sqrt{98} \)
- Simplify \( \sqrt{200} \)
Mathjax Formulas
To write the above simplification using Mathjax, use the following codes:
- Prime factorization: \( 72 = 2^3 \times 3^2 \)
- Pairs: \( 2^2 \times 3^2 \times \sqrt{2} \)
- Simplified: \( 6\sqrt{2} \)
Additional Tips
- Always check for the largest square factor to simplify more efficiently.
- Practice regularly to get comfortable with the process.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental skill in mathematics that allows us to express roots in their simplest form. By understanding the process, you can handle more complex equations and enhance your overall math skills. Here, we provide a detailed introduction to simplifying square roots, explaining the concept and steps involved.
A square root is a value that, when multiplied by itself, gives the original number. For example, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \). Simplifying square roots involves expressing this root in the most reduced form possible.
To simplify a square root, follow these steps:
- Identify the number under the square root (the radicand).
- Perform prime factorization on the radicand to find its prime factors.
- Group the prime factors into pairs.
- Move each pair of prime factors outside the square root as a single factor.
- Multiply the factors outside the square root together.
- Keep any remaining factors inside the square root.
Let's illustrate this with an example:
- Consider the square root of 72: \( \sqrt{72} \).
- Prime factorize 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Group the prime factors into pairs: \( (2 \times 2) \) and \( (3 \times 3) \).
- Move the pairs outside the square root: \( 2 \) and \( 3 \).
- Multiply the factors outside: \( 2 \times 3 = 6 \).
- The simplified form is \( 6\sqrt{2} \), with 2 remaining inside the square root.
Understanding these steps will make simplifying square roots a straightforward task. Practice with different numbers to become proficient in this essential mathematical technique.
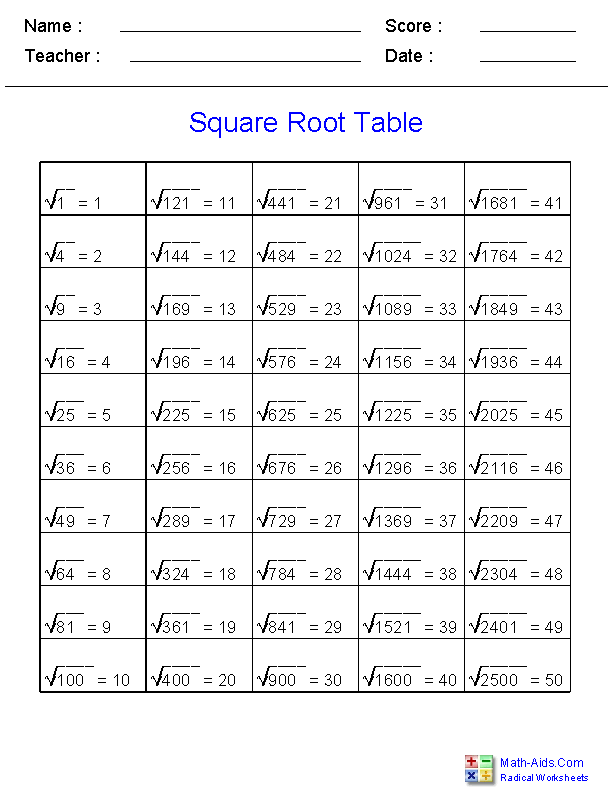
Understanding Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. The square root is denoted by the radical symbol √. For example, the square root of 16 is 4 because 4 × 4 = 16.
Here are some key concepts to understand square roots better:
- Perfect Squares: These are numbers that have integer square roots. Examples include 1, 4, 9, 16, 25, etc.
- Non-Perfect Squares: These numbers do not have integer square roots and result in irrational numbers when square rooted. Examples include 2, 3, 5, 7, 8, etc.
- Principal Square Root: The non-negative square root of a number. For example, the principal square root of 9 is 3, even though -3 is also a square root of 9.
To represent square roots mathematically, we use the radical symbol. Below is a simple representation:
\[ \sqrt{n} \]
Where \( n \) is the number for which we are finding the square root. Let's look at a few examples:
| Number (n) | Square Root (√n) |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
For non-perfect squares, the square roots are often represented in their simplified radical form. For instance:
- \( \sqrt{2} \approx 1.414 \)
- \( \sqrt{3} \approx 1.732 \)
- \( \sqrt{5} \approx 2.236 \)
Understanding the properties and representation of square roots is fundamental to simplifying square roots and performing more complex mathematical operations involving radicals.
Basic Concepts of Simplifying Square Roots
Simplifying square roots involves reducing the square root to its simplest form. Here are the basic steps to understand and simplify square roots:
Steps to Simplify Square Roots
- Factor the number under the square root:
Break down the number inside the square root (radicand) into its prime factors.
- Example: \(\sqrt{72}\) can be factored as \(\sqrt{2 \times 2 \times 2 \times 3 \times 3}\).
- Pair the prime factors:
Group the prime factors into pairs of identical numbers.
- Example: \(\sqrt{2 \times 2 \times 2 \times 3 \times 3}\) can be grouped as \((2 \times 2) \times 2 \times (3 \times 3)\).
- Move pairs outside the square root:
For every pair of identical numbers, move one number outside the square root.
- Example: \(\sqrt{(2 \times 2) \times 2 \times (3 \times 3)} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
Examples of Simplifying Square Roots
- \(\sqrt{18}\):
Factor 18 into \(2 \times 3 \times 3\).
Group as \(\sqrt{(3 \times 3) \times 2}\).
Simplify to \(3\sqrt{2}\).
- \(\sqrt{50}\):
Factor 50 into \(2 \times 5 \times 5\).
Group as \(\sqrt{(5 \times 5) \times 2}\).
Simplify to \(5\sqrt{2}\).
- \(\sqrt{72}\):
Factor 72 into \(2 \times 2 \times 2 \times 3 \times 3\).
Group as \(\sqrt{(2 \times 2) \times 2 \times (3 \times 3)}\).
Simplify to \(6\sqrt{2}\).
Simplifying Square Roots of Fractions
When dealing with fractions under a square root, apply the following rule:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Example: \(\sqrt{\frac{16}{9}} = \frac{\sqrt{16}}{\sqrt{9}} = \frac{4}{3}\).
Common Mistakes to Avoid
- Not fully factoring the radicand before simplifying.
- Incorrectly grouping factors or missing pairs.
- Leaving a square root in the denominator of a fraction without rationalizing it.
Practice Problems
- Simplify \(\sqrt{32}\)
- Simplify \(\sqrt{200}\)
- Simplify \(\sqrt{\frac{45}{81}}\)
Prime Factorization Method
The prime factorization method is a systematic way to simplify square roots by breaking down the number into its prime factors. Here are the steps to follow:
-
Factorize the Number into Prime Factors:
Start by dividing the number by the smallest prime number (usually 2) that can exactly divide it without leaving a remainder. Continue this process with the quotient until you reach a prime number.
Example:
To factorize 72:
- 72 ÷ 2 = 36
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
The prime factors of 72 are: \(2^3 \times 3^2\).
-
Organize the Prime Factors into Pairs:
Arrange the prime factors and pair identical factors. If a factor does not have a pair, it remains single.
Example:
From the prime factors \(2^3 \times 3^2\):
- Pairs: (2, 2), (2), (3, 3)
-
Multiply One Element from Each Pair:
Select one prime from each pair and multiply them. If a prime remains unpaired, it stays under the square root.
Example:
Pairs: (2, 2), (3, 3)
Multiplication result: \(2 \times 3 = 6\)
Since the prime factor 2 is unpaired, it remains under the square root: \(6 \sqrt{2}\).
-
Calculate the Square Root:
Multiply the results of the previous step together, and multiply this product by the square root of any leftover unpaired primes.
Example:
The square root of 72 is \(6 \sqrt{2}\).
Examples
Example 1: Square Root of 144
- Prime Factorization: \(144 = 2^4 \times 3^2\)
- Pairs: (2, 2), (2, 2), (3, 3)
- Multiplication result: \(2 \times 2 \times 3 = 12\)
- Square Root: \(\sqrt{144} = 12\)
Example 2: Square Root of 200
- Prime Factorization: \(200 = 2^3 \times 5^2\)
- Pairs: (2, 2), (5, 5)
- Multiplication result: \(2 \times 5 = 10\)
- Square Root: \(\sqrt{200} = 10 \sqrt{2}\)
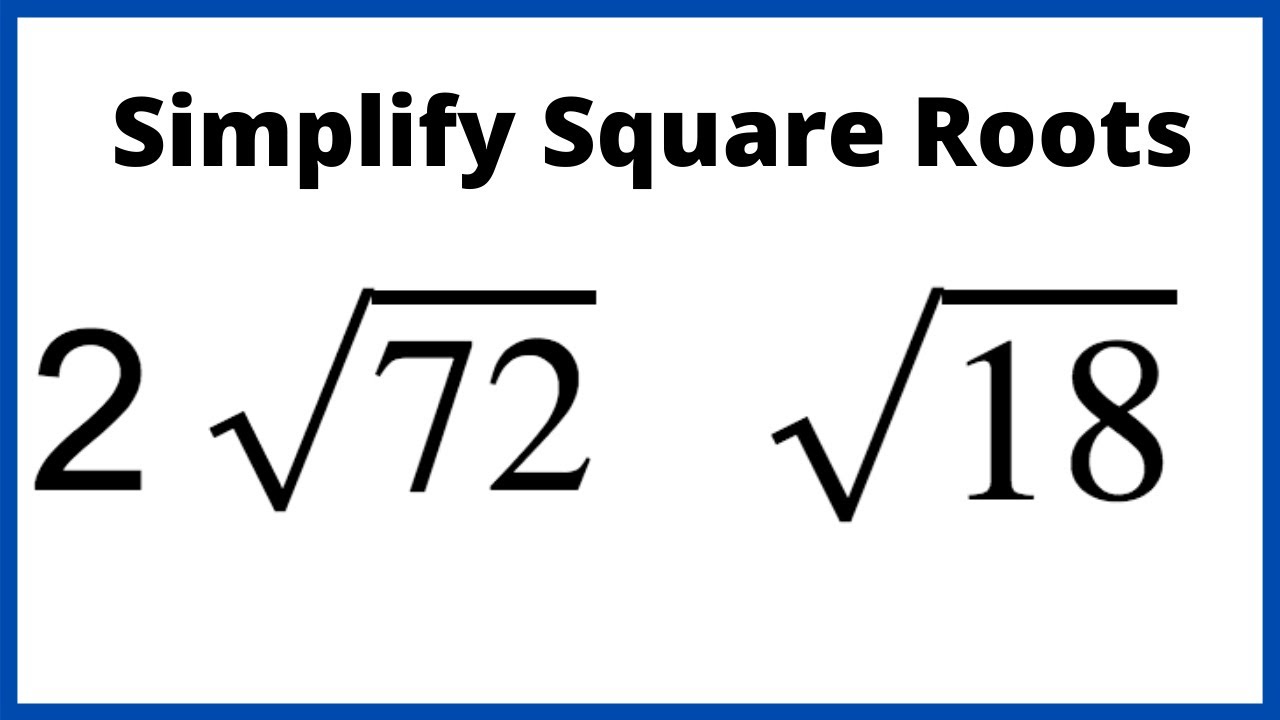
Step-by-Step Guide to Simplifying Square Roots
Simplifying square roots can be made easy by following a series of steps. Here is a detailed guide to help you through the process:
-
Identify Perfect Squares:
Find the largest perfect square factor of the number inside the square root. Perfect squares are numbers like 1, 4, 9, 16, 25, etc.
- Example: To simplify \(\sqrt{50}\), recognize that 50 can be factored into 25 and 2, where 25 is a perfect square.
-
Rewrite the Square Root:
Express the square root as the product of the square roots of its factors.
- Example: \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2}\)
-
Simplify the Square Roots:
Simplify the square root of the perfect square factor.
- Example: \(\sqrt{25} \times \sqrt{2} = 5 \sqrt{2}\)
This means \(\sqrt{50}\) simplifies to \(5\sqrt{2}\).
Examples
Let's go through a few more examples:
-
Simplify \(\sqrt{18}\):
- Identify perfect square factors: \(18 = 9 \times 2\)
- Rewrite the square root: \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2}\)
- Simplify: \(\sqrt{9} \times \sqrt{2} = 3 \sqrt{2}\)
Thus, \(\sqrt{18}\) simplifies to \(3\sqrt{2}\).
-
Simplify \(\sqrt{72}\):
- Identify perfect square factors: \(72 = 36 \times 2\)
- Rewrite the square root: \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2}\)
- Simplify: \(\sqrt{36} \times \sqrt{2} = 6 \sqrt{2}\)
Thus, \(\sqrt{72}\) simplifies to \(6\sqrt{2}\).
Fractions Involving Square Roots
Simplifying square roots in fractions follows a similar process using the quotient property of square roots:
\(\sqrt{\dfrac{a}{b}} = \dfrac{\sqrt{a}}{\sqrt{b}}\)
Example: Simplify \(\sqrt{\dfrac{50}{2}}\):
- Simplify the fraction inside the square root: \(\dfrac{50}{2} = 25\)
- Take the square root of the numerator and denominator separately: \(\sqrt{25} = 5\)
Thus, \(\sqrt{\dfrac{50}{2}} = 5\).
By following these steps, you can simplify square roots accurately and efficiently.
Examples of Simplifying Square Roots
Understanding how to simplify square roots through examples can make the concept clearer. Here are several step-by-step examples:
Example 1: Simplifying \(\sqrt{72}\)
- First, find the prime factors of 72:
- \(72 = 2 \times 2 \times 2 \times 3 \times 3\)
- Group the prime factors into pairs:
- \((2 \times 2) \times (3 \times 3) \times 2\)
- Take one number from each pair out of the square root:
- \(\sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Example 2: Simplifying \(\sqrt{200}\)
- Find the prime factors of 200:
- \(200 = 2 \times 2 \times 2 \times 5 \times 5\)
- Group the prime factors into pairs:
- \((2 \times 2) \times (5 \times 5) \times 2\)
- Take one number from each pair out of the square root:
- \(\sqrt{200} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2}\)
Example 3: Simplifying \(\sqrt{48}\)
- Find the prime factors of 48:
- \(48 = 2 \times 2 \times 2 \times 2 \times 3\)
- Group the prime factors into pairs:
- \((2 \times 2) \times (2 \times 2) \times 3\)
- Take one number from each pair out of the square root:
- \(\sqrt{48} = 2 \times 2 \times \sqrt{3} = 4\sqrt{3}\)
Example 4: Simplifying \(\sqrt{180}\)
- Find the prime factors of 180:
- \(180 = 2 \times 2 \times 3 \times 3 \times 5\)
- Group the prime factors into pairs:
- \((2 \times 2) \times (3 \times 3) \times 5\)
- Take one number from each pair out of the square root:
- \(\sqrt{180} = 2 \times 3 \times \sqrt{5} = 6\sqrt{5}\)
Common Mistakes and How to Avoid Them
Simplifying square roots can be straightforward, but several common mistakes can lead to errors. Here are some of these mistakes and how to avoid them:
- Overlooking Perfect Squares: One frequent mistake is not recognizing perfect squares within the radicand. For example, in \(\sqrt{18}\), the number 9 is a perfect square. Correct simplification: \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\).
- Misapplying Properties: Incorrectly using the properties of square roots, such as assuming \(\sqrt{a} + \sqrt{b} = \sqrt{a + b}\), is incorrect. The properties of square roots apply to multiplication and division, not addition and subtraction.
- Ignoring Variables: When simplifying expressions with variables, it's important to simplify them just as with numerical coefficients. For instance, \(\sqrt{x^4} = x^2\) since \(x^4\) is a perfect square.
- Simplification Errors: Errors in factorization or arithmetic operations can lead to incorrect results. Always double-check each step of your work.
- Forgetting to Rationalize the Denominator: Leaving a square root in the denominator is often considered an incomplete simplification. For example, \(\frac{1}{\sqrt{2}}\) should be rationalized to \(\frac{\sqrt{2}}{2}\).
To avoid these mistakes:
- Always look for perfect squares within the radicand.
- Review and apply the properties of square roots correctly.
- Ensure to simplify variables along with numerical coefficients.
- Double-check your arithmetic and factorization steps.
- Rationalize the denominator when necessary.
By being mindful of these common errors and following these tips, you can improve your accuracy in simplifying square roots and enhance your overall mathematical skills.
Practice Problems for Simplifying Square Roots
Practicing simplification of square roots helps solidify understanding and improve skills. Here are several problems to work on:
- Simplify \(\sqrt{50}\).
- Simplify \(\sqrt{72}\).
- Simplify \(\sqrt{200}\).
- Simplify \(\sqrt{98}\).
- Simplify \(\sqrt{32}\).
- Simplify \(\sqrt{128}\).
- Simplify \(\sqrt{450}\).
- Simplify \(\sqrt{108}\).
Answers:
- \(\sqrt{50} = 5\sqrt{2}\)
- \(\sqrt{72} = 6\sqrt{2}\)
- \(\sqrt{200} = 10\sqrt{2}\)
- \(\sqrt{98} = 7\sqrt{2}\)
- \(\sqrt{32} = 4\sqrt{2}\)
- \(\sqrt{128} = 8\sqrt{2}\)
- \(\sqrt{450} = 15\sqrt{2}\)
- \(\sqrt{108} = 6\sqrt{3}\)
More practice problems:
- \(\sqrt{75}\)
- \(\sqrt{150}\)
- \(\sqrt{245}\)
- \(\sqrt{180}\)
- \(\sqrt{288}\)
Keep practicing to master the skill of simplifying square roots!

Advanced Techniques for Simplifying Square Roots
While basic techniques for simplifying square roots involve prime factorization, advanced techniques often include methods such as rationalizing the denominator, using properties of exponents, and manipulating complex numbers. Below, we outline some of these advanced methods step-by-step.
Rationalizing the Denominator
Rationalizing the denominator involves removing a square root from the denominator of a fraction. Here's how to do it:
Identify the radical in the denominator: For example, in the fraction \( \frac{1}{\sqrt{2}} \), the denominator is \( \sqrt{2} \).
Multiply the numerator and denominator by the same radical: Multiply both the numerator and denominator by \( \sqrt{2} \) to get \( \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} \).
Simplify: This results in \( \frac{\sqrt{2}}{2} \) because \( \sqrt{2} \cdot \sqrt{2} = 2 \).
Using Properties of Exponents
Square roots can also be simplified using exponent rules. Here’s an example:
Express the square root as an exponent: For \( \sqrt{x^4} \), rewrite it as \( x^{4/2} \).
Simplify the exponent: \( x^{4/2} = x^2 \).
Manipulating Complex Numbers
When dealing with negative numbers under the square root, you need to use complex numbers:
Express the square root of a negative number using \( i \): For example, \( \sqrt{-4} \) can be written as \( 2i \), since \( \sqrt{4} = 2 \) and \( \sqrt{-1} = i \).
Simplify: Combine the coefficients with the imaginary unit, \( i \).
Examples
Simplify \( \sqrt{50} \):
- Prime factorize \( 50 = 2 \times 5^2 \).
- Separate the perfect square: \( \sqrt{50} = \sqrt{2 \times 25} = 5\sqrt{2} \).
Simplify \( \frac{3}{\sqrt{5}} \):
- Multiply by \( \sqrt{5} \) over \( \sqrt{5} \): \( \frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5} \).
Simplify \( \sqrt{-9} \):
- Express as a complex number: \( \sqrt{-9} = 3i \).
Practice Problems
- Simplify \( \sqrt{200} \).
- Simplify \( \frac{5}{\sqrt{7}} \).
- Simplify \( \sqrt{-16} \).
Applications of Simplified Square Roots in Real Life
Simplified square roots have numerous practical applications across various fields. Understanding these applications can help illustrate the importance and utility of square roots in real-world scenarios.
Finance
In finance, square roots are used to calculate stock market volatility, a measure of how much a stock's price varies over time. The variance of stock returns is square-rooted to determine the standard deviation, which investors use to assess the risk of an investment.
Architecture and Engineering
Square roots play a crucial role in architecture and engineering. For example, they are used to calculate the natural frequency of structures, such as bridges and buildings, to predict how they will respond to different loads like wind or traffic.
Science
Various scientific calculations involve square roots, such as determining the velocity of moving objects, the amount of radiation absorbed by materials, and the intensity of sound waves. These calculations help scientists understand natural phenomena and develop new technologies.
Statistics
In statistics, square roots are essential for calculating standard deviation, a measure of how spread out data points are from the mean. The standard deviation is the square root of the variance, helping statisticians analyze data sets and make informed decisions.
Geometry
Geometry frequently uses square roots to compute the area and perimeter of shapes and solve problems involving right triangles, such as using the Pythagorean theorem to find the length of a triangle's sides.
Computer Science and Cryptography
In computer science, square roots are used in algorithms for encryption, image processing, and game physics. Cryptography employs square roots in digital signatures, key exchange systems, and secure communication channels to ensure data security.
Navigation
Square roots are applied in navigation to compute distances between points on a map and to estimate directions. Pilots and sailors use these calculations to determine the best routes and distances for travel.
Electrical Engineering
In electrical engineering, square roots are used to calculate power, voltage, and current in circuits. These calculations are crucial for designing and developing electrical systems like power grids and communication networks.
Cooking
Recipes often require adjustments in ingredient quantities when scaling up. The square root of the scaling factor helps maintain the correct proportions of ingredients, ensuring the dish retains its intended flavor.
Photography
The aperture of a camera lens, which controls the amount of light entering the camera, is expressed as an f-number. The area of the aperture is proportional to the square of the f-number, affecting the light exposure in photography.
Computer Graphics
In 2D and 3D graphics, square roots are used to calculate distances between points and the length of vectors, essential for rendering accurate images and animations.
Telecommunication
In telecommunications, the signal strength decreases as the distance from the transmitter increases, following the inverse square law. This principle is critical for designing effective communication systems.
Overall, square roots are integral to many disciplines, providing essential tools for calculations and problem-solving in various real-life applications.
Additional Resources and Practice Worksheets
Here are some valuable resources and practice worksheets to help you master the skill of simplifying square roots:
-
Interactive Tutorials and Videos
- - This resource offers a detailed explanation and examples of how to simplify square roots using the prime factorization method, along with interactive elements to aid understanding.
- - Provides video lessons and step-by-step instructions on simplifying square roots by factoring out perfect squares and using the product rule.
- - Includes examples and exercises on using the product and quotient rules to simplify square roots, along with a math solver for practice.
-
Practice Worksheets
- - Offers printable worksheets for practicing the simplification of square roots, including exercises on prime factorization and identifying perfect squares.
- - A comprehensive PDF worksheet that includes a variety of problems to reinforce your skills in simplifying square roots.
- - Provides a range of worksheets focusing on simplifying square roots, suitable for different skill levels and offering ample practice.
-
Online Calculators and Solvers
- - This tool can help you check your work and understand the steps involved in simplifying square roots.
- - An advanced computational engine that can simplify square roots and provide detailed explanations of the process.
Using these resources and practice worksheets will help you develop a strong understanding of how to simplify square roots, identify common mistakes, and apply advanced techniques effectively.
Conclusion and Summary
Simplifying square roots is a fundamental skill in mathematics that can make solving complex equations more manageable. By breaking down a number into its prime factors and using the properties of square roots, we can express these roots in their simplest form. Here's a summary of the key points covered in this guide:
- Understanding Square Roots: The square root of a number \( \sqrt{n} \) is a value that, when multiplied by itself, gives the number \( n \). Every positive number has two square roots: one positive and one negative, denoted by \( \sqrt{n} \) and \( -\sqrt{n} \), respectively.
- Basic Concepts: Simplifying square roots involves expressing a number in its simplest radical form, such as converting \( \sqrt{12} \) to \( 2\sqrt{3} \) by factoring out the largest perfect square.
- Prime Factorization Method: By breaking down the radicand (the number under the square root sign) into its prime factors, you can simplify the square root. For example, \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \) because \( 18 = 9 \times 2 \) and \( \sqrt{9} = 3 \).
-
Step-by-Step Guide:
- Factor the number into prime factors.
- Pair the prime factors.
- Move one factor from each pair outside the square root.
- Multiply the factors outside the square root.
- Common Mistakes: Avoid mistakes such as forgetting to simplify completely, or incorrectly factoring the radicand. Always check your work by squaring the simplified form to ensure it equals the original radicand.
- Advanced Techniques: More complex expressions, such as those involving variables or multiple radicals, can also be simplified using similar principles. For example, \( \sqrt{2x^2} \) simplifies to \( x\sqrt{2} \) assuming \( x \) is non-negative.
- Real-Life Applications: Simplified square roots are useful in various fields including physics, engineering, and finance, where they help in simplifying formulas and solving equations more efficiently.
By mastering these techniques, you can confidently tackle mathematical problems involving square roots. Keep practicing with different types of problems to strengthen your understanding and proficiency.
For further practice and additional resources, refer to worksheets and online tutorials to reinforce these concepts. Simplifying square roots is a valuable skill that will aid in your mathematical journey.

Hướng dẫn Cách Đơn Giản Hóa Căn Bậc Hai
Hướng dẫn Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Hướng dẫn Cách Đơn Giản Hóa Căn Bậc Hai
Hướng dẫn Cách Đơn Giản Hóa Căn Bậc Hai