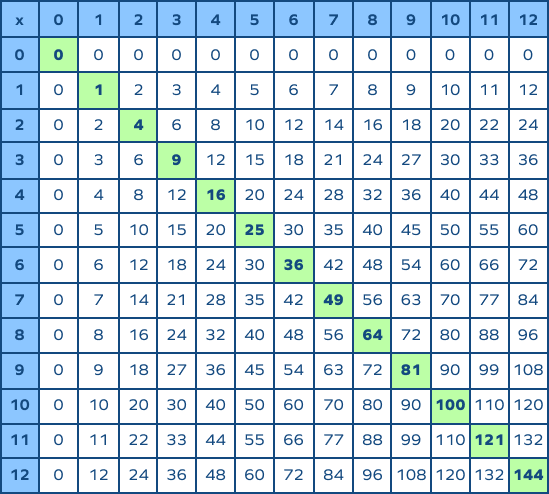
Topic how to reduce square roots: Learning how to reduce square roots is a fundamental skill in mathematics that simplifies complex expressions. This guide will walk you through various methods to simplify square roots efficiently, enhancing your problem-solving skills and mathematical understanding.
Table of Content
- How to Reduce Square Roots
- Introduction to Simplifying Square Roots
- Prime Factorization Method
- Identifying Perfect Squares
- Step-by-Step Simplification Process
- Examples of Simplifying Common Square Roots
- Simplifying Square Roots with Coefficients
- Dealing with Variables Inside Square Roots
- Handling Square Roots in Fractions
- Common Mistakes to Avoid
- Practice Problems and Solutions
- Advanced Techniques for Simplifying Square Roots
- Applications of Simplified Square Roots in Real Life
- Additional Resources and Tools
- Conclusion
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai để thu hút người xem.
How to Reduce Square Roots
Reducing square roots involves simplifying the expression under the square root symbol to its simplest form. This process can be broken down into several steps:
Step-by-Step Guide
- Find Prime Factors:
Break down the number inside the square root into its prime factors. For example, 12 can be broken down into 2 × 2 × 3.
- Pair the Factors:
Group the prime factors into pairs. For example, in the case of 12: 2 × 2 × 3, we can pair 2 × 2.
- Simplify the Pairs:
Move each pair of prime factors outside the square root as a single factor. For instance, √(2 × 2 × 3) simplifies to 2√3.
- Multiply Remaining Factors:
Multiply any remaining factors that are inside the square root. For example, √(2 × 2 × 5) simplifies to 2√5.
Examples
| Expression | Simplified Form |
|---|---|
| √12 | 2√3 |
| √45 | 3√5 |
| √72 | 6√2 |
| √200 | 10√2 |
Dealing with Coefficients
If the expression has a coefficient outside the square root, such as 3√72, treat the coefficient separately. Simplify the square root first and then multiply the result by the coefficient:
3√72 = 3 × 6√2 = 18√2
Handling Variables
When dealing with variables under the square root, factor them as well. For example:
√(12x2y4) = 2xy2√3
Radicals in Fractions
Simplify square roots in fractions by combining and then simplifying:
√30 / √10 = √(30 / 10) = √3
By following these steps, you can simplify square roots efficiently.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots involves reducing the number inside the square root to its smallest possible form. This process makes calculations easier and results more manageable. Understanding how to simplify square roots is a fundamental skill in algebra and higher-level math. Below are the detailed steps and methods to simplify square roots effectively.
- Identify Perfect Squares: Determine if there are any perfect square factors in the number under the square root.
- Factorization: Break down the number into its prime factors.
- Separate Perfect Squares: Using the property of square roots, separate the perfect squares from the non-perfect squares.
- Simplify: Take the square root of the perfect square factors and multiply them outside the square root symbol.
For example, to simplify √72:
- Factor 72 into its prime factors: 72 = 2 × 2 × 2 × 3 × 3.
- Identify the perfect squares: 2 × 2 and 3 × 3.
- Separate the perfect squares: √(2² × 3² × 2).
- Simplify: √(2²) × √(3²) × √2 = 2 × 3 × √2 = 6√2.
By following these steps, you can simplify square roots for any given number, ensuring that your results are as simplified as possible.
Prime Factorization Method
The prime factorization method is a systematic way to simplify square roots by breaking down the number under the square root into its prime factors. This method ensures the number inside the square root is expressed in its simplest form.
- Find Prime Factors: Begin by finding the prime factors of the number inside the square root. For example, to simplify \( \sqrt{72} \):
- 72 can be factored into prime numbers: \( 72 = 2 \times 36 = 2 \times 2 \times 18 = 2 \times 2 \times 2 \times 9 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Pair the Factors: Group the prime factors into pairs. Each pair of prime factors can be taken out of the square root as a single number. For \( \sqrt{72} \):
- We have the pairs: \( (2 \times 2) \) and another \( (2 \times 2) \) and \( 3 \times 3 \).
- Simplify the Expression: Take one number from each pair out of the square root. Multiply these numbers together outside the square root. Any number that does not have a pair remains inside the square root. For \( \sqrt{72} \):
- From the pairs: \( \sqrt{2 \times 2 \times 2 \times 3 \times 3} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
- Combine the Results: Combine the numbers taken out of the square root to get the simplified form. For \( \sqrt{72} \):
- The simplified form is \( 6\sqrt{2} \).
This method can be applied to any square root to reduce it to its simplest form, making calculations easier and more efficient.
Identifying Perfect Squares
Simplifying square roots often involves identifying perfect squares within the number under the radical sign. A perfect square is a number that can be expressed as the square of an integer. For example, 1, 4, 9, 16, 25, and 36 are perfect squares because they are squares of 1, 2, 3, 4, 5, and 6 respectively.
To simplify a square root, follow these steps:
-
List all factors of the number under the square root.
-
Identify the factors that are perfect squares. Choose the largest perfect square factor.
-
Rewrite the square root as the product of the square roots of the factors.
-
Simplify the square roots where possible.
For example, to simplify \(\sqrt{72}\):
-
List the factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.
-
Identify the perfect squares: 1, 4, 9, 36 (the largest perfect square factor is 36).
-
Rewrite \(\sqrt{72}\) as \(\sqrt{36 \times 2}\).
-
Simplify: \(\sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\).
Therefore, \(\sqrt{72} = 6\sqrt{2}\).
Step-by-Step Simplification Process
Learning how to simplify square roots can make solving mathematical problems much easier. Follow this step-by-step process to simplify square roots effectively:
- Identify if the number inside the square root is a perfect square or can be factored into perfect squares.
- Break down the number into its prime factors.
- Group the prime factors into pairs.
- For each pair of identical factors, take one factor out of the square root.
- Multiply the factors outside the square root and leave the unpaired factors inside the square root.
Here are detailed steps with examples:
- Step 1: Identify if the number is a perfect square or factorable.
- Step 2: Break down the number into prime factors. For example, for √72:
- Step 3: Group the prime factors into pairs.
- Step 4: Take one factor out of each pair.
- Step 5: Multiply the factors outside the square root.
\[ 72 = 2 \times 2 \times 2 \times 3 \times 3 \]
\[ \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} \]
\[ \sqrt{72} = 2 \times 3 \times \sqrt{2} \]
\[ \sqrt{72} = 6\sqrt{2} \]
This simplified form is easier to work with in further calculations.

Examples of Simplifying Common Square Roots
Simplifying square roots can be done by factoring the number under the square root sign into its prime factors and then applying the square root to those factors. Here are some detailed examples of how to simplify common square roots step-by-step:
-
Example 1: Simplify \(\sqrt{72}\)
- Factor 72 into its prime factors: \(72 = 2 \times 2 \times 2 \times 3 \times 3\).
- Pair the prime factors: \( \sqrt{72} = \sqrt{(2 \times 2) \times (2 \times 3 \times 3)} \).
- Take one factor out of each pair: \( \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
-
Example 2: Simplify \(\sqrt{45}\)
- Factor 45 into its prime factors: \(45 = 3 \times 3 \times 5\).
- Pair the prime factors: \( \sqrt{45} = \sqrt{(3 \times 3) \times 5} \).
- Take one factor out of each pair: \( \sqrt{(3 \times 3) \times 5} = 3\sqrt{5} \).
-
Example 3: Simplify \(\sqrt{50}\)
- Factor 50 into its prime factors: \(50 = 2 \times 5 \times 5\).
- Pair the prime factors: \( \sqrt{50} = \sqrt{2 \times (5 \times 5)} \).
- Take one factor out of each pair: \( \sqrt{2 \times (5 \times 5)} = 5\sqrt{2} \).
-
Example 4: Simplify \(\sqrt{98}\)
- Factor 98 into its prime factors: \(98 = 2 \times 7 \times 7\).
- Pair the prime factors: \( \sqrt{98} = \sqrt{2 \times (7 \times 7)} \).
- Take one factor out of each pair: \( \sqrt{2 \times (7 \times 7)} = 7\sqrt{2} \).
These steps can be applied to any number under the square root sign to simplify it effectively. By practicing these examples, you will become more comfortable with simplifying square roots using the prime factorization method.
Simplifying Square Roots with Coefficients
Simplifying square roots with coefficients involves a step-by-step approach to break down the expression into a simpler form. Here's a detailed guide to help you through the process:
-
Identify the Coefficient: Start by identifying the coefficient and the square root part of the expression. For example, in \( 3\sqrt{50} \), the coefficient is 3 and the square root part is \( \sqrt{50} \).
-
Simplify the Square Root: Simplify the square root by finding its prime factors. For \( \sqrt{50} \), we find the prime factors of 50: \( 50 = 2 \times 5 \times 5 \). Thus, \( \sqrt{50} = \sqrt{2 \times 5^2} \).
-
Separate the Perfect Square: Rewrite the square root to separate the perfect square. Using the example, \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \).
-
Multiply the Coefficient: Multiply the coefficient by the simplified square root. Therefore, \( 3\sqrt{50} \) simplifies to \( 3 \times 5\sqrt{2} = 15\sqrt{2} \).
By following these steps, you can simplify any square root expression with a coefficient. Practice with different numbers to become more comfortable with the process.
Dealing with Variables Inside Square Roots
Simplifying square roots that contain variables involves applying the same principles used in simplifying numerical square roots, but with extra attention to the variables. Here’s a detailed, step-by-step guide on how to handle these square roots:
- Understand the Square Root Rule:
The square root of a product is the product of the square roots. This means:
\[\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\]
- Separate Variables and Numbers:
When you have a square root that includes both numbers and variables, break them down into separate square roots.
Example: \(\sqrt{50x^4}\) can be separated as \(\sqrt{50} \cdot \sqrt{x^4}\)
- Simplify the Numerical Part:
First, simplify the numerical part using prime factorization or by identifying perfect squares.
Example: \(\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\)
- Simplify the Variable Part:
For the variable part, use the property that \(\sqrt{x^n} = x^{n/2}\).
Example: \(\sqrt{x^4} = x^{4/2} = x^2\)
- Combine the Simplified Parts:
After simplifying both the numerical and variable parts, combine them back together.
Example: \(\sqrt{50x^4} = 5\sqrt{2} \cdot x^2 = 5x^2\sqrt{2}\)
Examples:
- \(\sqrt{18y^6}\)
Separate into \(\sqrt{18} \cdot \sqrt{y^6}\)
Simplify: \(\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\)
Simplify: \(\sqrt{y^6} = y^{6/2} = y^3\)
Combine: \(\sqrt{18y^6} = 3y^3\sqrt{2}\)
- \(\sqrt{45a^8}\)
Separate into \(\sqrt{45} \cdot \sqrt{a^8}\)
Simplify: \(\sqrt{45} = \sqrt{9 \cdot 5} = 3\sqrt{5}\)
Simplify: \(\sqrt{a^8} = a^{8/2} = a^4\)
Combine: \(\sqrt{45a^8} = 3a^4\sqrt{5}\)
By following these steps, you can simplify square roots involving variables effectively. Practice with different expressions to master this technique.
Handling Square Roots in Fractions
Simplifying square roots in fractions involves applying properties of square roots and fractions. Here’s a detailed, step-by-step guide on how to handle these square roots:
- Understand the Square Root of a Fraction Rule:
The square root of a fraction is the square root of the numerator divided by the square root of the denominator:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
- Simplify the Numerator and Denominator Separately:
First, simplify the square root of the numerator and the denominator separately, if possible.
Example: \(\sqrt{\frac{50}{18}}\)
Simplify: \(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\)
Simplify: \(\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\)
- Combine the Simplified Parts:
Place the simplified square roots of the numerator and denominator back into the fraction.
Example: \(\sqrt{\frac{50}{18}} = \frac{5\sqrt{2}}{3\sqrt{2}}\)
- Simplify the Fraction:
If there are common factors in the numerator and the denominator, simplify the fraction further.
Example: \(\frac{5\sqrt{2}}{3\sqrt{2}} = \frac{5}{3}\)
Examples:
- \(\sqrt{\frac{32}{8}}\)
Simplify the numerator: \(\sqrt{32} = \sqrt{16 \cdot 2} = 4\sqrt{2}\)
Simplify the denominator: \(\sqrt{8} = \sqrt{4 \cdot 2} = 2\sqrt{2}\)
Combine: \(\sqrt{\frac{32}{8}} = \frac{4\sqrt{2}}{2\sqrt{2}}\)
Simplify the fraction: \(\frac{4\sqrt{2}}{2\sqrt{2}} = 2\)
- \(\sqrt{\frac{45}{20}}\)
Simplify the numerator: \(\sqrt{45} = \sqrt{9 \cdot 5} = 3\sqrt{5}\)
Simplify the denominator: \(\sqrt{20} = \sqrt{4 \cdot 5} = 2\sqrt{5}\)
Combine: \(\sqrt{\frac{45}{20}} = \frac{3\sqrt{5}}{2\sqrt{5}}\)
Simplify the fraction: \(\frac{3\sqrt{5}}{2\sqrt{5}} = \frac{3}{2}\)
By following these steps, you can simplify square roots in fractions effectively. Practice with different fractions to master this technique.

Common Mistakes to Avoid
When simplifying square roots, it's easy to make mistakes that can lead to incorrect answers. Here are some common mistakes and tips on how to avoid them:
- Forgetting to Simplify Completely:
Sometimes, people stop simplifying too early. Ensure that you factor out all perfect squares.
Example: Simplifying \(\sqrt{72}\).
Incorrect: \(\sqrt{72} = 6\sqrt{2}\)
Correct: \(\sqrt{72} = \sqrt{36 \cdot 2} = 6\sqrt{2}\)
- Incorrectly Splitting the Square Root:
Remember the rule \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\). Misapplying this can lead to errors.
Example: \(\sqrt{50}\)
Incorrect: \(\sqrt{50} = \sqrt{5} \cdot \sqrt{10}\)
Correct: \(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\)
- Ignoring Negative Signs:
Square roots of negative numbers involve imaginary numbers, which need to be handled properly.
Example: \(\sqrt{-4}\)
Incorrect: \(\sqrt{-4} = -2\)
Correct: \(\sqrt{-4} = 2i\)
- Misunderstanding Square Roots of Variables:
Apply the rule \(\sqrt{x^n} = x^{n/2}\) correctly, especially when dealing with even and odd powers.
Example: \(\sqrt{x^6}\)
Incorrect: \(\sqrt{x^6} = x^3\)
Correct: \(\sqrt{x^6} = x^{6/2} = x^3\)
- Incorrectly Handling Fractions:
Ensure to split the square root of a fraction correctly into the square root of the numerator and the square root of the denominator.
Example: \(\sqrt{\frac{9}{16}}\)
Incorrect: \(\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{9}{16}\)
Correct: \(\sqrt{\frac{9}{16}} = \frac{3}{4}\)
- Forgetting to Rationalize the Denominator:
Leaving a square root in the denominator is often considered improper. Rationalize the denominator by multiplying by a suitable form of 1.
Example: \(\frac{1}{\sqrt{2}}\)
Incorrect: \(\frac{1}{\sqrt{2}}\)
Correct: \(\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
By being aware of these common mistakes and knowing how to avoid them, you can simplify square roots more accurately and confidently. Practice regularly to strengthen your skills.
Practice Problems and Solutions
Practicing how to simplify square roots can help you become more proficient and confident in handling these types of problems. Below are some practice problems along with step-by-step solutions.
Problem 1: Simplify √50
- Prime factorize 50: 50 = 2 × 5 × 5.
- Group the prime factors into pairs: 50 = 2 × (5 × 5).
- Identify the perfect square: 5 × 5 = 25, which is a perfect square.
- Rewrite the square root: √50 = √(2 × 25) = √2 × √25.
- Simplify the perfect square: √25 = 5, so √50 = 5√2.
Answer: √50 = 5√2
Problem 2: Simplify √72
- Prime factorize 72: 72 = 2 × 2 × 2 × 3 × 3.
- Group the prime factors into pairs: 72 = (2 × 2) × (3 × 3) × 2.
- Identify the perfect squares: 2 × 2 = 4 and 3 × 3 = 9.
- Rewrite the square root: √72 = √(4 × 9 × 2) = √4 × √9 × √2.
- Simplify the perfect squares: √4 = 2 and √9 = 3, so √72 = 2 × 3 × √2 = 6√2.
Answer: √72 = 6√2
Problem 3: Simplify √98
- Prime factorize 98: 98 = 2 × 7 × 7.
- Group the prime factors into pairs: 98 = 2 × (7 × 7).
- Identify the perfect square: 7 × 7 = 49, which is a perfect square.
- Rewrite the square root: √98 = √(2 × 49) = √2 × √49.
- Simplify the perfect square: √49 = 7, so √98 = 7√2.
Answer: √98 = 7√2
Problem 4: Simplify 3√18
- Prime factorize 18: 18 = 2 × 3 × 3.
- Group the prime factors into pairs: 18 = 2 × (3 × 3).
- Identify the perfect square: 3 × 3 = 9, which is a perfect square.
- Rewrite the square root: √18 = √(2 × 9) = √2 × √9.
- Simplify the perfect square: √9 = 3, so √18 = 3√2.
- Combine with the coefficient: 3√18 = 3 × 3√2 = 9√2.
Answer: 3√18 = 9√2
Problem 5: Simplify √32
- Prime factorize 32: 32 = 2 × 2 × 2 × 2 × 2.
- Group the prime factors into pairs: 32 = (2 × 2) × (2 × 2) × 2.
- Identify the perfect squares: 2 × 2 = 4 and 2 × 2 = 4.
- Rewrite the square root: √32 = √(4 × 4 × 2) = √4 × √4 × √2.
- Simplify the perfect squares: √4 = 2, so √32 = 2 × 2√2 = 4√2.
Answer: √32 = 4√2
Practice Problems
- Simplify √45
- Simplify √27
- Simplify √75
- Simplify 2√50
- Simplify 5√8
Try to solve these problems on your own and then compare your solutions with the steps outlined above. Happy practicing!
Advanced Techniques for Simplifying Square Roots
Simplifying square roots can become more intricate as we delve into advanced techniques. Here are some methods and examples:
1. Using Rationalization
Rationalizing the denominator involves eliminating the square root from the denominator of a fraction. For example:
- Given: \( \frac{1}{\sqrt{2}} \)
- Multiply the numerator and the denominator by \( \sqrt{2} \): \( \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2} \)
2. Denesting Radicals
Denesting refers to expressing a nested radical in a simpler form. For example, for \( \sqrt{a} \pm \sqrt{b} \):
- Given: \( \sqrt{2} + \sqrt{3} \)
- Assume: \( \sqrt{2} + \sqrt{3} = \sqrt{x} + \sqrt{y} \)
- Find \( x \) and \( y \) such that \( \sqrt{2} + \sqrt{3} = \sqrt{3/2} + \sqrt{1/2} \)
3. Using Higher Index Roots
When simplifying higher-index roots, look for factors with powers that match the index. For instance, simplifying \( \sqrt[4]{16y^4} \):
- Rewrite as: \( \sqrt[4]{(2^4)(y^4)} \)
- Separate: \( \sqrt[4]{2^4} \cdot \sqrt[4]{y^4} = 2y \)
4. Combining Like Terms
Combine radicals that have the same radicand. For example:
- Given: \( 2\sqrt{3} + 3\sqrt{3} \)
- Combine: \( (2 + 3)\sqrt{3} = 5\sqrt{3} \)
5. Simplifying Radicals with Variables
Simplify by factoring out squares. For example, \( \sqrt{12x^6y^3} \):
- Rewrite: \( \sqrt{(2^2 \cdot 3)(x^3)^2 \cdot y^2 \cdot y} \)
- Simplify: \( 2x^3y\sqrt{3y} \)
Examples
- Simplify \( \sqrt{72} \)
Step-by-step:
- List factors: \( 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 \)
- Largest perfect square factor: \( 36 \)
- Rewrite: \( \sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2} \)
- Simplify \( \sqrt[3]{54} \)
Step-by-step:
- Rewrite: \( \sqrt[3]{27 \cdot 2} = \sqrt[3]{27} \cdot \sqrt[3]{2} = 3\sqrt[3]{2} \)
By mastering these advanced techniques, you can simplify even the most complex square roots.
Applications of Simplified Square Roots in Real Life
Square roots are not just abstract mathematical concepts; they have numerous practical applications in various fields. Here are some of the ways simplified square roots are utilized in real-life scenarios:
- Engineering and Architecture:
Square roots are essential in calculating distances and dimensions. For instance, in structural engineering, the Pythagorean theorem is used to determine the lengths of various components, ensuring stability and safety. The natural frequency of structures like bridges and buildings can be determined using square roots, which helps predict their behavior under different loads.
- Finance:
In finance, square roots are used to calculate volatility, which is a measure of how much a stock's price fluctuates. This involves taking the square root of the variance of a stock's returns, helping investors assess the risk associated with an investment.
- Statistics:
Square roots are fundamental in statistical analysis for calculating the standard deviation, a measure of the dispersion of a set of values. This helps in understanding how spread out the values in a data set are around the mean.
- Physics:
In physics, square roots are used in various calculations, such as determining the intensity of sound waves, the amount of radiation absorbed by a material, and the velocity of moving objects. These calculations are crucial for developing new technologies and scientific understanding.
- Computer Science:
In computer science, square roots are used in algorithms for encryption, image processing, and game physics. For instance, the distance formula, which involves square roots, is used in graphics to determine the distance between two points in 2D and 3D space.
- Navigation:
Square roots are used in navigation to calculate distances between points on a map. The distance formula, derived from the Pythagorean theorem, is used by pilots and sailors to plan routes and determine the shortest path between destinations.
- Quadratic Equations:
The quadratic formula, which includes a square root, is used to solve quadratic equations. This is particularly useful in fields like physics, engineering, and economics, where such equations often model real-world scenarios.
- Geometry:
Square roots are used to calculate the area and perimeter of various shapes. For example, in right triangles, the lengths of the sides are often determined using square roots through the Pythagorean theorem.
- Electrical Engineering:
In electrical engineering, square roots are used to compute power, voltage, and current in circuits. These calculations are critical for designing and developing electrical systems and devices.
These examples demonstrate the versatility and importance of square roots in solving practical problems across different disciplines, highlighting their value beyond the classroom.
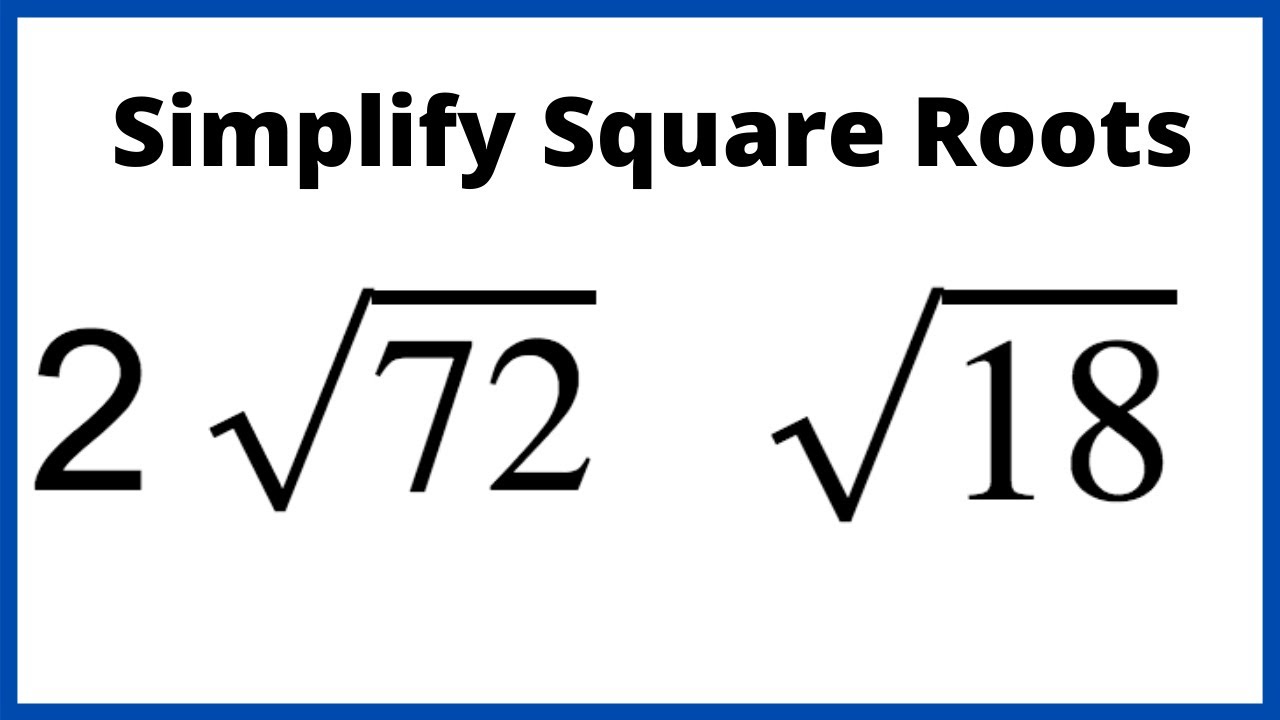
Additional Resources and Tools
Here are some useful resources and tools to help you further understand and simplify square roots:
Online Calculators
-
This tool reduces any square root to its simplest radical form and calculates the approximation of the root. It's useful for quick calculations and verifying your work.
-
Symbolab offers a comprehensive calculator that not only simplifies square roots but also provides step-by-step solutions. Great for learning the process and understanding each step.
-
Mathway's calculator allows you to enter a radical expression and find its square root. It provides exact and decimal forms of the results, making it easy to compare and understand different forms.
Educational Websites
-
Khan Academy offers detailed lessons and practice problems on simplifying square roots, complete with video tutorials to guide you through the concepts.
-
Purplemath provides in-depth explanations and examples of simplifying radicals, covering both basic and advanced techniques.
-
This site offers a simple and intuitive guide to understanding and simplifying square roots, with interactive examples to practice.
Practice Worksheets
-
Math-Drills provides printable worksheets for practicing square root simplification, ranging from basic to more complex problems.
-
Generate custom worksheets to practice simplifying radicals, aligned with Common Core standards.
Interactive Tools
-
Desmos is a powerful graphing calculator that can help visualize square roots and their simplifications. It's great for exploring how changes in expressions affect their simplifications.
-
GeoGebra provides interactive tools for learning and teaching mathematics, including capabilities to explore and simplify square roots visually.
Books
-
The Art of Problem Solving, Volume 1: The Basics by Sandor Lehoczky and Richard Rusczyk
This book offers a comprehensive introduction to problem-solving, including techniques for simplifying square roots.
-
Pre-Algebra by Richard Rusczyk
A great resource for middle school students that covers square roots and their simplifications in detail.
Conclusion
Simplifying square roots is a fundamental skill in mathematics, offering both theoretical and practical applications. Throughout this guide, we have explored various methods and techniques to simplify square roots effectively.
By understanding and applying the prime factorization method, recognizing perfect squares, and mastering advanced techniques such as rationalizing denominators and working with variables, students can handle complex square root problems with confidence.
Here are the key takeaways:
- Prime Factorization: Break down the number under the square root into its prime factors and pair them to simplify.
- Perfect Squares: Identify and extract perfect square factors to simplify the square root.
- Advanced Techniques: Learn and apply techniques like rationalizing denominators and dealing with variables inside square roots to tackle more complex problems.
Practicing with a variety of problems and utilizing additional resources and tools will enhance your proficiency in simplifying square roots. Understanding these methods not only helps in academic settings but also in real-life applications where square roots are used in fields such as engineering, physics, and finance.
With consistent practice and a solid grasp of the concepts, you will find that simplifying square roots becomes second nature, allowing you to solve mathematical problems more efficiently and accurately. Keep exploring, practicing, and applying these techniques to continue improving your skills.
Thank you for following this comprehensive guide. We hope it has provided you with valuable insights and tools to simplify square roots effectively. Happy learning!
Hướng dẫn cách đơn giản hóa căn bậc hai để thu hút người xem.
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Hướng dẫn đơn giản hóa căn bậc hai cùng Thầy J để thu hút người xem.
Đơn Giản Hóa Căn Bậc Hai | Toán với Thầy J