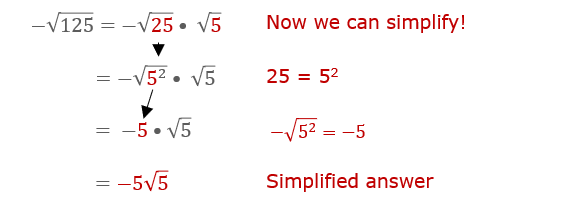Topic simplify square roots worksheet pdf: Discover the best way to master simplifying square roots with our comprehensive worksheets available in PDF format. Perfect for students and teachers alike, these worksheets offer clear instructions, step-by-step solutions, and a variety of problems to practice. Start simplifying square roots with confidence and improve your math skills today!
Table of Content
- Simplify Square Roots Worksheets
- Introduction to Square Roots
- Basic Concepts of Square Roots
- How to Simplify Square Roots
- Steps to Simplify Square Roots
- Examples of Simplifying Square Roots
- Simplifying Square Roots with Variables
- Higher Roots Simplification
- Rationalizing the Denominator
- Common Mistakes and How to Avoid Them
- Practice Problems with Solutions
- Interactive Quizzes and Worksheets
- Video Tutorials for Simplifying Square Roots
- Additional Resources and References
- Conclusion and Next Steps
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai một cách dễ dàng và chi tiết. Video này phù hợp cho người học toán và các bài tập về đơn giản hóa căn bậc hai.
Simplify Square Roots Worksheets
Welcome to our collection of worksheets designed to help you simplify square roots. These resources are perfect for students looking to improve their skills in handling square roots in mathematical expressions.
Worksheet Features
- Comprehensive exercises for simplifying square roots
- Step-by-step solutions included
- Printable PDF format for easy access
- Suitable for various grade levels
Topics Covered
Our worksheets cover a range of topics related to simplifying square roots, including:
- Basic simplification of square roots
- Simplifying square roots with variables
- Simplifying higher roots
- Rationalizing the denominator
Example Problems
Here are some examples of the types of problems you will encounter in our worksheets:
Download Your Worksheets
Click the links below to download the worksheets in PDF format:
Why Practice Simplifying Square Roots?
Simplifying square roots is a crucial skill in algebra and higher-level math. It helps students:
- Understand the properties of radicals
- Prepare for solving quadratic equations
- Improve problem-solving skills
- Build a strong foundation for advanced math topics
Additional Resources
For further learning, explore these additional resources:

READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics that involve finding a number which, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \(5 \times 5 = 25\). This operation is crucial in various areas of math and science, including algebra, geometry, and calculus.
Understanding square roots begins with recognizing perfect squares, such as 1, 4, 9, 16, and 25. A perfect square is a number that can be expressed as the product of an integer with itself. For instance:
- \(1 = 1 \times 1\)
- \(4 = 2 \times 2\)
- \(9 = 3 \times 3\)
- \(16 = 4 \times 4\)
- \(25 = 5 \times 5\)
To simplify square roots, you can use the prime factorization method or the method of identifying perfect square factors. Here is a step-by-step guide to simplifying square roots:
- Factor the number inside the square root into its prime factors. For example, \(48 = 2 \times 2 \times 2 \times 2 \times 3\).
- Group the prime factors into pairs of identical factors. In our example, \(48 = (2 \times 2) \times (2 \times 2) \times 3\).
- Take the square root of each pair of identical factors and move them outside the square root sign. This gives us \(2 \times 2 \times \sqrt{3}\).
- Multiply the numbers outside the square root sign. Thus, \(2 \times 2 \times \sqrt{3} = 4\sqrt{3}\).
If the number inside the square root (the radicand) does not contain any perfect square factors, the square root cannot be simplified further. For instance, \(\sqrt{19}\) remains \(\sqrt{19}\) because 19 is a prime number and has no perfect square factors.
Learning and memorizing the perfect squares up to 100 can significantly aid in simplifying square roots. Here's a quick reference:
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
- \(\sqrt{36} = 6\)
- \(\sqrt{49} = 7\)
- \(\sqrt{64} = 8\)
- \(\sqrt{81} = 9\)
- \(\sqrt{100} = 10\)
In summary, understanding and simplifying square roots are essential skills in mathematics, useful for simplifying expressions and solving equations. Practice with square root worksheets can reinforce these concepts and help you become proficient in this area.
Basic Concepts of Square Roots
Understanding square roots is fundamental in mathematics. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because \(4 \times 4 = 16\). In mathematical notation, this is written as \(\sqrt{16} = 4\).
Here are some key concepts to help you understand square roots better:
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because they are the squares of whole numbers (1, 2, 3, 4, and 5, respectively).
- Non-Perfect Squares: Numbers like 2, 3, 5, and 10 are not perfect squares and their square roots are irrational numbers, which cannot be expressed as exact fractions and have non-repeating decimal parts.
- Square Root Symbol: The symbol for the square root is \(\sqrt{\ }\). For example, \(\sqrt{25} = 5\).
- Simplifying Square Roots: To simplify a square root, you break down the number inside the square root into its prime factors and then simplify. For example, \(\sqrt{48} = \sqrt{16 \times 3} = 4\sqrt{3}\).
Let's look at the steps to simplify square roots:
- Factor the Number: Express the number inside the square root as the product of its prime factors. For example, \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2}\).
- Simplify Each Factor: Take the square root of each perfect square factor. In our example, \(\sqrt{36} \times \sqrt{2} = 6\sqrt{2}\).
Additionally, here is a table of common perfect squares:
| Number | Perfect Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
Memorizing the perfect squares up to at least 100 can greatly help in simplifying square roots quickly and accurately.
How to Simplify Square Roots
Simplifying square roots involves breaking down the number under the square root (radicand) into its prime factors and simplifying those factors. Here's a step-by-step guide to simplify square roots:
-
Find the Prime Factors:
Express the radicand as a product of its prime factors. For example, for √72, the prime factors are 2, 2, 2, 3, and 3 because 72 = 2 × 2 × 2 × 3 × 3.
-
Group the Factors:
Pair the prime factors into groups of two. Using the example above, √72 can be written as √(2 × 2 × 2 × 3 × 3).
-
Extract Perfect Squares:
Each pair of identical factors under the square root can be taken out as a single factor. In the case of √72, the pairs are (2 × 2) and (3 × 3). Taking these out gives 2 and 3, respectively.
-
Multiply the Factors:
Multiply the factors that have been taken out of the square root. Here, it becomes 2 × 3. Any remaining factors that do not form pairs stay inside the square root. For √72, the remaining factor is 2, resulting in the simplified form of 6√2.
-
Simplify the Result:
Combine the simplified factors. For √72, the final simplified form is 6√2.
Here's a summary table for better understanding:
| Step | Example | Explanation |
|---|---|---|
| Prime Factorization | √72 | 72 = 2 × 2 × 2 × 3 × 3 |
| Group Factors | √(2 × 2) × (3 × 3) × 2 | Pair up the factors: (2 × 2) and (3 × 3) |
| Extract Perfect Squares | 2 × 3 × √2 | Each pair (2 × 2 and 3 × 3) is taken out as 2 and 3 |
| Multiply Factors | 6√2 | 2 × 3 = 6, remaining factor inside the square root is 2 |
By following these steps, you can simplify any square root effectively. Practice with different examples to master this technique!
Steps to Simplify Square Roots
Simplifying square roots can seem challenging, but by following a systematic approach, it becomes much easier. Below are the detailed steps to simplify square roots:
-
Prime Factorization:
First, break down the number under the square root (radicand) into its prime factors. For example, to simplify √180, start by finding its prime factors: 180 = 2 × 2 × 3 × 3 × 5.
-
Identify and Pair Factors:
Look for pairs of identical factors. Each pair of identical factors can be taken out of the square root as a single factor. In our example, √180 can be rewritten as √(2 × 2 × 3 × 3 × 5).
-
Extract and Simplify:
Take one factor from each pair out of the square root, and multiply them together. For √180, the pairs are (2 × 2) and (3 × 3). Taking one from each pair gives us 2 and 3. Multiplying these, we get 6. The remaining factor, 5, stays inside the square root. Thus, √180 simplifies to 6√5.
-
Verify and Simplify Further:
Ensure there are no further simplifications possible. Check that the radicand inside the square root does not contain any more perfect square factors. In our example, 5 is already a prime number, so no further simplification is needed.
To illustrate these steps, consider another example: Simplify √50.
- Prime Factorization: 50 = 2 × 5 × 5
- Identify and Pair Factors: √(2 × 5 × 5)
- Extract and Simplify: Take the pair (5 × 5) out as 5, leaving 2 inside the square root. So, √50 = 5√2.
- Verify: 2 is a prime number, so no further simplification is possible.
By mastering these steps, you can simplify any square root with ease.
Examples of Simplifying Square Roots
Here are some detailed examples that illustrate how to simplify square roots step-by-step:
Example 1: Simplify √72
- Prime Factorization:
Break down 72 into its prime factors:
\(72 = 2 \times 2 \times 2 \times 3 \times 3\)
- Pair and Simplify:
Identify pairs of identical factors. In this case, we have pairs of 2's and 3's:
\(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Example 2: Simplify √50
- Prime Factorization:
Break down 50 into its prime factors:
\(50 = 2 \times 5 \times 5\)
- Pair and Simplify:
Identify pairs of identical factors. Here, we have one pair of 5's:
\(\sqrt{50} = \sqrt{2 \times (5 \times 5)} = 5 \sqrt{2}\)
Example 3: Simplify √98
- Prime Factorization:
Break down 98 into its prime factors:
\(98 = 2 \times 7 \times 7\)
- Pair and Simplify:
Identify pairs of identical factors. In this case, we have one pair of 7's:
\(\sqrt{98} = \sqrt{2 \times (7 \times 7)} = 7 \sqrt{2}\)
Example 4: Simplify √200
- Prime Factorization:
Break down 200 into its prime factors:
\(200 = 2 \times 2 \times 2 \times 5 \times 5\)
- Pair and Simplify:
Identify pairs of identical factors. Here, we have pairs of 2's and 5's:
\(\sqrt{200} = \sqrt{(2 \times 2) \times 2 \times (5 \times 5)} = 2 \times 5 \times \sqrt{2} = 10 \sqrt{2}\)
These examples demonstrate the process of breaking down the radicand into prime factors, identifying pairs, and simplifying the square root by extracting those pairs.
Simplifying Square Roots with Variables
Simplifying square roots involving variables follows a similar process as simplifying numerical square roots. The key steps are to factor the expression inside the square root and then apply the properties of square roots. Here’s how you can simplify square roots with variables:
-
Factor the radicand (expression inside the square root):
Break down the radicand into its prime factors, including both numerical and variable components.
- For example, in \( \sqrt{50x^2} \), factor \( 50 \) as \( 2 \times 5 \times 5 \) and \( x^2 \) as \( x \times x \).
-
Group the factors into pairs:
Identify pairs of factors inside the radicand. Each pair will come out of the square root as a single factor.
- Continuing the example, \( \sqrt{50x^2} \) becomes \( \sqrt{(5 \times 5) \times 2 \times x \times x} \).
- Here, \( 5 \times 5 \) and \( x \times x \) are pairs.
-
Bring each pair outside the square root:
For each pair of factors, bring one factor outside the square root. If there are no pairs, the factor remains inside the square root.
- In our example, bring out \( 5 \) and \( x \), resulting in \( 5x \sqrt{2} \).
-
Simplify the expression:
Combine the factors outside the square root and leave the remaining factors inside. The simplified form of \( \sqrt{50x^2} \) is \( 5x \sqrt{2} \).
Let’s look at another example:
- Consider \( \sqrt{72y^3} \).
- Factorize \( 72 \) into \( 2^3 \times 3^2 \) and \( y^3 \) into \( y^2 \times y \).
- Group into pairs: \( \sqrt{(2^2 \times 3^2) \times 2 \times y^2 \times y} \).
- Bring out the pairs: \( 2 \times 3 \times y = 6y \).
- Combine: \( 6y \sqrt{2y} \).
So, \( \sqrt{72y^3} \) simplifies to \( 6y \sqrt{2y} \).
By following these steps, you can simplify any square root expression that includes variables.
Higher Roots Simplification
When simplifying higher roots such as cube roots (\(\sqrt[3]{x}\)) or fourth roots (\(\sqrt[4]{x}\)), the process involves a few more steps than simplifying square roots. Here’s a detailed guide to help you through it:
-
Identify the Radicand:
Look at the number or expression inside the radical sign. This is called the radicand. For example, in \(\sqrt[3]{54}\), 54 is the radicand.
-
Factor the Radicand into Prime Factors:
Break down the radicand into its prime factors. For instance, \(54 = 2 \times 3^3\).
-
Group the Factors According to the Root:
Group the prime factors into sets that match the index of the root. For a cube root, you would group in sets of three. In our example: \(54 = 2 \times 3^3 = 3 \times \sqrt[3]{2}\).
-
Simplify the Root:
Take one factor out of the radical for each complete group. Using the example \(\sqrt[3]{54}\), since \(3^3\) is a complete group, it comes out as 3: \(3 \sqrt[3]{2}\).
-
Check for Further Simplification:
Ensure there are no other factors that can be grouped or simplified further. If so, repeat the process.
Let's see some examples:
| Expression | Prime Factorization | Simplified Form |
|---|---|---|
| \(\sqrt[3]{128}\) | \(2^7 = (2^3)^2 \times 2\) | \(4 \sqrt[3]{2}\) |
| \(\sqrt[4]{80y^{14}}\) | \(2^4 \times 5 \times (y^3)^4 \times y^2\) | \(2|y^3| \sqrt[4]{5y^2}\) |
| \(\sqrt[3]{\frac{a^8}{a^5}}\) | \(\frac{a^3}{1}\) | \(a\) |
Using these steps, you can simplify any higher root. The key is to break down the radicand into manageable parts and methodically simplify each part according to the index of the root.
Rationalizing the Denominator
Rationalizing the denominator involves rewriting a fraction so that the denominator is a rational number. This is often necessary when the denominator contains a square root or another irrational number. The process ensures that the expression is in its simplest form and is easier to work with in further calculations.
Here are the steps to rationalize the denominator:
- Identify the irrational denominator. For example, in the fraction \( \frac{1}{\sqrt{2}} \), the denominator is \( \sqrt{2} \).
- Multiply both the numerator and the denominator by the conjugate of the denominator. The conjugate of \( \sqrt{2} \) is \( \sqrt{2} \). So, multiply as follows: \[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
- Simplify the expression if possible. In this case, \( \frac{\sqrt{2}}{2} \) is already simplified.
For a more complex example, consider rationalizing the denominator of \( \frac{3}{2 + \sqrt{5}} \). Follow these steps:
- Multiply both the numerator and the denominator by the conjugate of the denominator, \( 2 - \sqrt{5} \): \[ \frac{3}{2 + \sqrt{5}} \times \frac{2 - \sqrt{5}}{2 - \sqrt{5}} \]
- Distribute in the numerator and apply the difference of squares formula in the denominator: \[ \frac{3(2 - \sqrt{5})}{(2 + \sqrt{5})(2 - \sqrt{5})} = \frac{6 - 3\sqrt{5}}{4 - 5} \]
- Simplify the expression: \[ \frac{6 - 3\sqrt{5}}{-1} = -6 + 3\sqrt{5} \]
To summarize, rationalizing the denominator transforms the fraction into a form that is more suitable for addition, subtraction, and further simplification. It ensures that expressions involving square roots are in their most manageable form.

Common Mistakes and How to Avoid Them
Simplifying square roots can be straightforward if approached correctly, but there are several common mistakes students often make. Here’s a guide to avoid these pitfalls:
- Forgetting to Simplify Completely
Ensure you break down the radicand into its prime factors and simplify completely. For example, \(\sqrt{50}\) should be simplified as:
\[
\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}
\] - Not Recognizing Perfect Squares
Recognize and factor out perfect squares. For instance, in \(\sqrt{72}\):
\[
\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}
\] - Improper Handling of Variables
When dealing with variables, remember to apply the square root to each part. For example, \(\sqrt{18x^2}\) should be:
\[
\sqrt{18x^2} = \sqrt{9 \times 2 \times x^2} = 3x\sqrt{2}
\] - Incorrectly Combining Terms
Only like terms can be combined. For example:
\[
2\sqrt{3} + 4\sqrt{3} = 6\sqrt{3}
\]
but
\[
2\sqrt{3} + 4\sqrt{5}
\]
cannot be combined. - Misunderstanding Rationalizing the Denominator
Ensure to multiply by the appropriate form of 1 to rationalize. For example, to rationalize \(\frac{1}{\sqrt{3}}\):
\[
\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\]
By being mindful of these common mistakes and practicing diligently, you can master the process of simplifying square roots.
Practice Problems with Solutions
Practicing simplifying square roots is essential to master the concept. Below are some practice problems along with their solutions to help you understand the process step-by-step.
| Problem | Solution |
|---|---|
| \(\sqrt{50}\) | \[ \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \] |
| \(\sqrt{72}\) | \[ \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \] |
| \(\sqrt{18x^2}\) | \[ \sqrt{18x^2} = \sqrt{9 \times 2 \times x^2} = \sqrt{9} \times \sqrt{2} \times \sqrt{x^2} = 3x\sqrt{2} \] |
| \(\frac{1}{\sqrt{3}}\) | \[ \frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3} \] |
| \(\sqrt{45}\) | \[ \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \] |
By practicing these problems, you can solidify your understanding of how to simplify square roots. Remember to factorize the number inside the square root and simplify step by step.
Interactive Quizzes and Worksheets
Engaging with interactive quizzes and worksheets is an effective way to master the concept of simplifying square roots. Below are some resources and activities designed to help students practice and improve their skills.
Online Quizzes
- Timed Quizzes: Test your speed and accuracy in simplifying square roots with timed quizzes.
- Multiple Choice: Choose the correct simplified form from multiple options.
- Step-by-Step Quizzes: Follow a guided process to simplify square roots, ensuring you understand each step.
Printable Worksheets
Downloadable PDF worksheets provide a variety of problems to solve, ranging from basic to advanced levels.
- : Focus on simplifying perfect squares and non-perfect squares.
- : Include a mix of integers, decimals, and fractions.
- : Challenge yourself with complex problems involving variables and higher roots.
Interactive Learning Tools
Utilize these tools to further enhance your understanding and practice of simplifying square roots:
- Square Root Calculator: Enter any number and see the step-by-step process to simplify its square root.
- Interactive Worksheets: Complete worksheets online and receive instant feedback on your answers.
- Video Tutorials: Watch expert explanations and demonstrations of various simplification techniques.
Practice Problems
| Problem | Solution |
|---|---|
| \(\sqrt{18}\) | \(3\sqrt{2}\) |
| \(\sqrt{50}\) | \(5\sqrt{2}\) |
| \(\sqrt{72}\) | \(6\sqrt{2}\) |
Additional Resources
For more practice and in-depth learning, explore these additional resources:
Video Tutorials for Simplifying Square Roots
Learning to simplify square roots can be greatly enhanced through visual aids. Video tutorials provide step-by-step guidance, making the concepts easier to understand and apply. Here are some recommended video tutorials:
-
Basic Simplification of Square Roots
This video covers the fundamental steps in simplifying square roots, including breaking down numbers into prime factors and identifying perfect squares.
-
Advanced Techniques
For those looking to deepen their understanding, this video explores more complex scenarios, such as simplifying square roots with variables and fractions.
-
Common Mistakes to Avoid
This tutorial highlights frequent errors students make when simplifying square roots and provides tips on how to avoid them.
These video tutorials are an excellent resource for visual learners and can be revisited as needed to reinforce the concepts. By watching these videos, students can gain confidence and improve their skills in simplifying square roots.

Additional Resources and References
For further learning and practice on simplifying square roots, consider exploring the following resources:
- Online Calculators: Utilize online square root calculators to verify your solutions and understand each step of the simplification process.
- PDF Worksheets: Download and practice with comprehensive worksheets available in PDF format. These often include a variety of problems with solutions to aid in self-assessment.
- Tutorial Videos: Watch detailed video tutorials that explain the concepts and steps involved in simplifying square roots.
- Interactive Quizzes: Test your knowledge with interactive quizzes that provide instant feedback and explanations for each question.
- Math Forums: Participate in math forums and discussion groups where you can ask questions and share insights about simplifying square roots.
These resources will help reinforce your understanding and provide ample practice opportunities to master the skill of simplifying square roots.
Conclusion and Next Steps
Congratulations on completing this comprehensive guide to simplifying square roots! You've learned about the fundamental concepts, various techniques, and common mistakes to avoid. Let's summarize the key points and outline your next steps for continued learning and practice.
Key Takeaways
- Understanding the square root and its properties.
- Mastering the steps to simplify square roots using prime factorization.
- Learning to rationalize the denominator to simplify expressions further.
- Avoiding common mistakes such as incorrect factorization and simplification errors.
Next Steps
- Practice Regularly: Consistent practice is crucial. Utilize the practice problems and solutions provided in this guide to reinforce your understanding.
- Use Online Resources: There are numerous online worksheets and interactive quizzes available to further enhance your skills. Explore websites like Cuemath and OnlineMathLearning for additional practice materials and explanations.
- Watch Tutorial Videos: Visual learning can be very effective. Search for video tutorials on platforms like YouTube to see step-by-step explanations of simplifying square roots.
- Join Study Groups: Engaging with peers can provide additional support and motivation. Join math study groups or forums to discuss problems and solutions.
- Consult Additional Resources: Reference books, online articles, and math websites can offer more in-depth explanations and examples. Utilize these resources to deepen your understanding.
Further Reading
- - Provides worksheets, interactive quizzes, and detailed explanations.
- - Offers printable worksheets and step-by-step tutorials.
- - Features video tutorials and practice exercises on various math topics.
With dedication and regular practice, you can master the art of simplifying square roots. Keep challenging yourself with more complex problems and continue exploring the fascinating world of mathematics. Happy learning!
Hướng dẫn cách đơn giản hóa căn bậc hai một cách dễ dàng và chi tiết. Video này phù hợp cho người học toán và các bài tập về đơn giản hóa căn bậc hai.
Cách Đơn Giản Hóa Căn Bậc Hai | Đối Tác Trong Toán Học
READ MORE:
Xem ngay video Đơn Giản Hóa Căn Bậc Hai Tờ Bài Tập Perfect Square Kuta để nắm bắt cách giải các bài tập về căn bậc hai một cách dễ dàng và nhanh chóng.
💥🛑💥DỪNG LẠI!💥🛑💥Đơn Giản Hóa Căn Bậc Hai Tờ Bài Tập Perfect Square Kuta