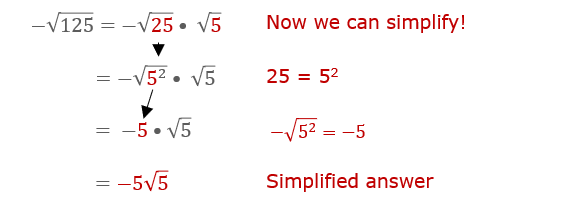Topic simplify square roots with exponents: Discover the easiest ways to simplify square roots with exponents. This guide provides step-by-step instructions, practical examples, and expert tips to help you master the art of simplifying radical expressions involving exponents. Whether you're a student or math enthusiast, you'll find valuable insights to enhance your understanding and skills.
Table of Content
- How to Simplify Square Roots with Exponents
- Introduction to Simplifying Square Roots
- Basics of Exponents and Roots
- Square Roots and Exponents
- Understanding Rational Exponents
- Step-by-Step Guide to Simplifying Square Roots
- Simplifying Square Roots with Fractions
- Simplifying Square Roots with Variables
- Quotient Property for Simplifying Square Roots
- Adding and Subtracting Radical Expressions
- Multiplying and Dividing Radical Expressions
- Special Cases: Perfect Squares and Cubes
- Converting Between Radical and Exponent Notation
- Examples and Practice Problems
- Common Mistakes and How to Avoid Them
- Advanced Techniques for Simplifying Radicals
- Applications of Simplified Radicals
- Summary and Key Takeaways
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc với biến số, số mũ, phân số và căn bậc ba. Học cách xử lý các biểu thức phức tạp trong đại số một cách hiệu quả.
How to Simplify Square Roots with Exponents
Simplifying square roots that involve exponents can often make complex expressions more manageable. Here’s a detailed guide on how to approach these simplifications using different methods and properties.
1. Using Rational Exponents
Square roots can be represented using rational exponents. The square root of a number is the same as raising that number to the power of 1/2. This notation can simplify multiplication and division of radicals.
- Example: \( \sqrt{a} = a^{\frac{1}{2}} \)
- Example: \( \sqrt[3]{a} = a^{\frac{1}{3}} \)
By converting roots to exponents, we can apply the laws of exponents more easily.
2. Properties of Square Roots
- Product Property: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \)
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
3. Simplifying Radicals with Variables
When simplifying square roots that include variables, it is important to apply the properties of exponents and square roots correctly.
- Example: \( \sqrt{a^2} = |a| \)
- Example: \( \sqrt{a^4} = a^2 \) since \( (a^2)^2 = a^4 \)
- Example: \( \sqrt{a^2 b^3} = a \cdot b \sqrt{b} \)
4. Step-by-Step Examples
Example 1: Simplify \( \sqrt{50} \)
- Factor 50 into prime factors: \( 50 = 2 \times 5^2 \).
- Apply the product property: \( \sqrt{50} = \sqrt{2 \times 5^2} \).
- Simplify: \( \sqrt{2} \cdot 5 = 5\sqrt{2} \).
Example 2: Simplify \( \sqrt{72x^5} \)
- Factor 72 and the variable expression: \( 72 = 2^3 \times 3^2 \) and \( x^5 = x^4 \times x \).
- Apply the product property: \( \sqrt{72x^5} = \sqrt{(2^3 \times 3^2) \times (x^4 \times x)} \).
- Simplify inside the radical: \( \sqrt{2^3 \times 3^2 \times x^4 \times x} = \sqrt{2^3} \times \sqrt{3^2} \times \sqrt{x^4} \times \sqrt{x} \).
- Simplify each term: \( \sqrt{2^3} = 2\sqrt{2} \), \( \sqrt{3^2} = 3 \), \( \sqrt{x^4} = x^2 \), and \( \sqrt{x} = \sqrt{x} \).
- Combine: \( 6x^2 \sqrt{2x} \).
5. Converting Between Radical and Exponent Notation
Sometimes, converting between radical notation and exponent notation can simplify the expression further. This involves expressing the roots as fractional exponents and vice versa.
| Radical Form | Exponent Form | Example |
|---|---|---|
| \( \sqrt{a} \) | \( a^{\frac{1}{2}} \) | \( \sqrt{16} = 16^{\frac{1}{2}} = 4 \) |
| \( \sqrt[3]{a} \) | \( a^{\frac{1}{3}} \) | \( \sqrt[3]{27} = 27^{\frac{1}{3}} = 3 \) |
By understanding and applying these principles, simplifying square roots with exponents becomes a more intuitive and manageable process.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental concept in algebra that involves rewriting square root expressions in their simplest form. This process often includes the use of exponent rules and properties of radicals. By mastering these techniques, students can handle more complex mathematical problems with ease. Below is a detailed guide on how to simplify square roots step by step.
To simplify a square root:
- Identify and factor the radicand (the number under the square root symbol) into its prime factors.
- Group the factors into pairs of equal factors.
- Move one factor from each pair outside the radical.
- Multiply the factors outside the radical and simplify the expression inside the radical, if possible.
Here's an example:
- Consider the square root of 72: \(\sqrt{72}\).
- Prime factorization of 72 is \(2 \times 2 \times 2 \times 3 \times 3\).
- Group the factors into pairs: \((2 \times 2) \times (3 \times 3) \times 2\).
- Move one factor from each pair outside the radical: \(2 \times 3 \times \sqrt{2}\).
- Simplify the expression: \(6\sqrt{2}\).
In some cases, the radicand may include variables:
- Simplify the expression inside the radical by factoring the variables.
- Use the properties of exponents to simplify the square roots involving variables.
Example with variables:
- Simplify \(\sqrt{50x^4y^3}\).
- Prime factorization and variables: \(50 = 2 \times 5 \times 5\) and \(x^4 = x^2 \times x^2\) and \(y^3 = y^2 \times y\).
- Group into pairs: \((5 \times 5) \times (x^2 \times x^2) \times y^2 \times (2 \times y)\).
- Move one factor from each pair outside the radical: \(5x^2y\sqrt{2y}\).
Understanding and applying these steps helps in efficiently simplifying square roots, making complex mathematical expressions more manageable.
Basics of Exponents and Roots
Understanding exponents and roots is fundamental to simplifying square roots with exponents. Here are the key concepts:
- Exponents: If a number is used as a factor multiple times, it can be expressed in exponential notation. For example, \( 5 \cdot 5 \cdot 5 \cdot 5 = 5^4 \).
- Positive Integer Exponents: When the exponent is a positive integer, it indicates how many times the base is multiplied by itself. For example, \( 3^2 = 3 \cdot 3 = 9 \).
- Square Roots: The square root of a number is a value that, when multiplied by itself, gives the original number. For example, \( \sqrt{25} = 5 \) because \( 5 \cdot 5 = 25 \).
- Perfect Squares: These are squares of integers. Examples include \( 1, 4, 9, 16, 25, \ldots \).
Here's a step-by-step guide to simplifying square roots using exponents:
- Identify the radicand (the number under the square root symbol).
- Factor the radicand into its prime factors.
- Group the prime factors into pairs.
- Take one factor from each pair out of the square root.
- Multiply the factors outside the square root to get the simplified form.
For example, to simplify \( \sqrt{72} \):
- Prime factorize \( 72 \): \( 72 = 2^3 \cdot 3^2 \).
- Group the factors: \( \sqrt{72} = \sqrt{(2^2 \cdot 2) \cdot 3^2} \).
- Take one factor from each pair: \( \sqrt{72} = 2 \cdot 3 \cdot \sqrt{2} \).
- Multiply the factors outside the square root: \( 2 \cdot 3 = 6 \).
- The simplified form is \( 6\sqrt{2} \).
Converting between radical and exponent notation can also simplify the process. For instance, \( \sqrt{a} \) can be written as \( a^{1/2} \). Applying the laws of exponents, such as \( (a^m)^n = a^{mn} \), helps in further simplification.
Practicing these steps with different numbers and expressions will enhance your understanding and proficiency in simplifying square roots with exponents.
Square Roots and Exponents
Understanding the relationship between square roots and exponents is fundamental in simplifying expressions. Here, we will explore the basics and provide a step-by-step guide to simplifying square roots using exponents.
Square roots are a type of radical expression, and they can be expressed using exponents. For example, the square root of a number \( n \) is written as \( \sqrt{n} \), which is equivalent to \( n^{1/2} \). This conversion is useful in simplifying more complex expressions involving roots and exponents.
Let's delve into the fundamental concepts:
- Radical Form: A square root can be written as \( \sqrt{a} \).
- Exponent Form: The same expression can be written with a fractional exponent as \( a^{1/2} \).
Here are some examples to illustrate the relationship:
| Radical Form | Exponent Form | Principal Root |
| \(\sqrt{16}\) | \(16^{1/2}\) | 4 |
| \(\sqrt{25}\) | \(25^{1/2}\) | 5 |
| \(\sqrt{100}\) | \(100^{1/2}\) | 10 |
Now, let's explore the steps to simplify square roots using exponents:
- Express the Square Root as an Exponent: Convert the square root into an exponent. For example, \( \sqrt{a} \) becomes \( a^{1/2} \).
- Apply the Exponent Rules: Use the properties of exponents to simplify the expression. For instance, if you have \( (a^{m/n}) \), you can rewrite it as \( \sqrt[n]{a^m} \).
- Simplify the Expression: Reduce the expression to its simplest form by performing the necessary arithmetic operations.
Let's consider an example:
Simplify \( \sqrt{32} \).
- Step 1: Express the square root as an exponent: \( 32^{1/2} \).
- Step 2: Factorize the base number if possible. Here, \( 32 = 2^5 \).
- Step 3: Apply the exponent rules: \( (2^5)^{1/2} = 2^{5/2} \).
- Step 4: Simplify the exponent: \( 2^{5/2} = 2^2 \cdot 2^{1/2} = 4\sqrt{2} \).
Therefore, \( \sqrt{32} \) simplifies to \( 4\sqrt{2} \).
This method can be applied to more complex expressions involving variables and higher-order roots, making it a versatile tool in algebra.
Understanding Rational Exponents
Rational exponents are a way to represent roots and powers in a unified form. Instead of using the radical sign, we use exponents that are fractions. This can simplify many mathematical operations.
For example, the square root of a number can be written using a rational exponent:
\[
\sqrt{a} = a^{1/2}
\]
Similarly, a cube root can be written as:
\[
\sqrt[3]{a} = a^{1/3}
\]
This notation is especially useful when dealing with more complex expressions, as it allows for the use of exponent rules to simplify calculations.
Here are the basic rules for working with rational exponents:
- Product of Powers: \((a^m)^n = a^{mn}\)
- Power of a Product: \((ab)^n = a^n b^n\)
- Quotient of Powers: \(\frac{a^m}{a^n} = a^{m-n}\)
- Power of a Quotient: \(\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}\)
These rules apply whether the exponents are integers or fractions. For example:
\[
(a^{1/2})^2 = a^{(1/2) \times 2} = a^1 = a
\]
Rational exponents make it easier to handle roots in algebraic operations, and understanding them is fundamental to simplifying expressions involving roots and exponents.

Step-by-Step Guide to Simplifying Square Roots
Simplifying square roots involves breaking down the radicand into its prime factors and then using the properties of square roots to simplify. Here is a step-by-step guide to help you through the process:
- Identify the radicand: The radicand is the number inside the square root symbol. For example, in \(\sqrt{50}\), the radicand is 50.
- Prime factorize the radicand: Break down the radicand into its prime factors. For example, the prime factorization of 50 is \(2 \times 5^2\).
- Group the prime factors: Group the prime factors into pairs. For example, \(2 \times 5^2\) can be grouped as \((5 \times 5) \times 2\).
- Simplify the square root: For each pair of prime factors, take one factor out of the square root. For example, \(\sqrt{(5 \times 5) \times 2} = 5 \sqrt{2}\).
Let's look at a few more examples:
- Example 1: Simplify \(\sqrt{72}\)
- Prime factorize 72: \(72 = 2^3 \times 3^2\)
- Group the factors: \(2^2 \times 2 \times 3^2 = (2 \times 2) \times (3 \times 3) \times 2\)
- Simplify: \(\sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}\)
- Example 2: Simplify \(\sqrt{18}\)
- Prime factorize 18: \(18 = 2 \times 3^2\)
- Group the factors: \(2 \times 3^2 = 3^2 \times 2\)
- Simplify: \(\sqrt{3^2 \times 2} = 3 \sqrt{2}\)
These steps can be applied to any square root to simplify it effectively. Practice with different numbers to become more comfortable with the process.
Simplifying Square Roots with Fractions
Simplifying square roots involving fractions is a crucial skill in algebra. This process often involves the use of both the product property and the quotient property of square roots. Here, we will detail the step-by-step method to simplify these expressions efficiently.
-
Identify the Expression:
Consider an expression like \(\sqrt{\frac{a}{b}}\), where both \(a\) and \(b\) are non-negative real numbers.
-
Simplify the Fraction:
Before applying the square root, simplify the fraction if possible. For example, if you have \(\sqrt{\frac{50}{18}}\), reduce the fraction to its simplest form, \(\frac{25}{9}\).
-
Apply the Quotient Property:
The quotient property of square roots states that \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\). Apply this to the simplified fraction. For example, \(\sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}}.\)
-
Simplify the Radicals:
Simplify the square roots in both the numerator and the denominator. For example, \(\frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3}\).
-
Combine Results:
The result is the simplified form of the original expression. So, \(\sqrt{\frac{50}{18}} = \frac{5}{3}\).
By following these steps, you can efficiently simplify any square root expression that involves fractions. This method ensures clarity and accuracy, making it easier to work with these types of problems in algebra.
Simplifying Square Roots with Variables
When simplifying square roots that contain variables, we follow similar rules to those used with numerical square roots, but we also need to consider the properties of exponents. Here is a step-by-step guide:
-
Identify Perfect Squares: Identify any perfect squares in the coefficient and the variable parts. For example, in the expression
√(50x^4y^2), recognize that 50 can be broken down into 25 and 2, where 25 is a perfect square. Similarly,x^4andy^2are also perfect squares. -
Rewrite Inside the Radical: Rewrite the expression under the square root as a product of perfect squares and any remaining factors.
√(50x^4y^2) = √(25 * 2 * x^4 * y^2) -
Separate the Square Roots: Use the property
√(a * b) = √a * √bto separate the square root into simpler parts.
√(25 * 2 * x^4 * y^2) = √25 * √2 * √x^4 * √y^2 -
Simplify Each Part: Simplify the square roots of the perfect squares.
√25 = 5,√x^4 = x^2, and√y^2 = y.
Thus,√25 * √2 * √x^4 * √y^2 = 5 * √2 * x^2 * y. -
Combine the Simplified Parts: Combine the simplified parts to get the final answer.
5x^2y√2
To summarize, the steps involve identifying and simplifying perfect squares in both the numerical coefficients and the variable exponents. This method ensures that the expression under the square root is as simplified as possible.
Here's another example for further clarity:
Simplify √(18a^3b^5):
- Identify perfect squares:
18 = 9 * 2,a^3 = a^2 * a, andb^5 = b^4 * b. - Rewrite under the radical:
√(9 * 2 * a^2 * a * b^4 * b) - Separate the square roots:
√9 * √2 * √a^2 * √a * √b^4 * √b - Simplify each part:
√9 = 3,√a^2 = a,√b^4 = b^2 - Combine the parts:
3ab^2√(2ab)
This approach helps in breaking down the problem and simplifying complex expressions involving variables under square roots.
Quotient Property for Simplifying Square Roots
The Quotient Property of Square Roots states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. This property is useful for simplifying expressions involving square roots of fractions.
Given non-negative numbers a and b where b is not zero, the property can be written as:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
Here is a step-by-step guide to using the Quotient Property to simplify square roots:
- Simplify the fraction inside the radical, if possible.
Check if there are any common factors in the numerator and denominator and simplify the fraction before applying the square root.
- Rewrite the expression using the Quotient Property.
Separate the square root of the fraction into the quotient of the square roots of the numerator and denominator.
- Simplify the square roots in the numerator and the denominator.
Simplify each square root individually. If either the numerator or the denominator is a perfect square, simplify it to its integer value.
Let's look at some examples to illustrate these steps:
Example 1
Simplify: \(\sqrt{\frac{18}{50}}\)
- First, simplify the fraction \(\frac{18}{50}\). The greatest common factor of 18 and 50 is 2, so we can simplify this to \(\frac{9}{25}\).
- Rewrite using the Quotient Property: \(\sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}}\).
- Simplify the square roots: \(\frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}\).
Example 2
Simplify: \(\sqrt{\frac{45x^4}{20x^2}}\)
- Simplify the fraction inside the radical: \(\frac{45x^4}{20x^2} = \frac{45}{20} \cdot \frac{x^4}{x^2} = \frac{9}{4} \cdot x^2\).
- Rewrite using the Quotient Property: \(\sqrt{\frac{9x^2}{4}} = \frac{\sqrt{9x^2}}{\sqrt{4}}\).
- Simplify the square roots: \(\frac{\sqrt{9x^2}}{\sqrt{4}} = \frac{3x}{2}\).
Example 3
Simplify: \(\sqrt{\frac{75y^3}{3y}}\)
- Simplify the fraction inside the radical: \(\frac{75y^3}{3y} = 25y^2\).
- Rewrite using the Quotient Property: \(\sqrt{25y^2}\).
- Simplify the square root: \(5y\).
Using the Quotient Property of Square Roots helps to break down and simplify complex radical expressions, making them easier to work with in algebraic equations and other mathematical contexts.

Adding and Subtracting Radical Expressions
Adding and subtracting radical expressions involves combining like radicals, which are radicals with the same index and radicand. Here are the detailed steps to add and subtract radical expressions:
-
Identify Like Radicals: Like radicals have the same index and the same radicand. For example, \(3\sqrt{2}\) and \(5\sqrt{2}\) are like radicals, while \(3\sqrt{2}\) and \(3\sqrt{3}\) are not.
-
Simplify Each Radical: Before adding or subtracting, ensure each radical is in its simplest form. Simplify by factoring out perfect squares.
- \(\sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\)
- \(\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\)
-
Combine Like Radicals: Add or subtract the coefficients of like radicals, keeping the radical part unchanged.
- \(3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2}\)
- \(7\sqrt{3} - 2\sqrt{3} = 5\sqrt{3}\)
-
Special Cases: If the radicals are not like, they cannot be combined. For example, \(3\sqrt{2} + 4\sqrt{3}\) remains as it is because the radicals are different.
Here are a few examples:
-
Example 1: Simplify \(2\sqrt{5} + 3\sqrt{5}\)
Since the radicals are like, combine the coefficients:
\(2\sqrt{5} + 3\sqrt{5} = 5\sqrt{5}\)
-
Example 2: Simplify \(4\sqrt{3} - \sqrt{12}\)
First, simplify \(\sqrt{12}\):
\(\sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}\)
Now combine the like radicals:
\(4\sqrt{3} - 2\sqrt{3} = 2\sqrt{3}\)
-
Example 3: Simplify \(5\sqrt{2} + 3\sqrt{8}\)
Simplify \(\sqrt{8}\):
\(\sqrt{8} = \sqrt{4 \cdot 2} = 2\sqrt{2}\)
Now combine the like radicals:
\(5\sqrt{2} + 3(2\sqrt{2}) = 5\sqrt{2} + 6\sqrt{2} = 11\sqrt{2}\)
Multiplying and Dividing Radical Expressions
Multiplying and dividing radical expressions involves several steps. These steps ensure that the expressions are simplified correctly. Below is a detailed guide on how to handle these operations:
Multiplying Radical Expressions
When multiplying radical expressions, the key rule is to multiply the coefficients (numbers outside the radicals) and the radicands (numbers inside the radicals) separately. Here are the steps:
- Multiply the coefficients together.
- Multiply the radicands together.
- Simplify the resulting radical expression if possible.
For example:
\[
(3\sqrt{5}) \cdot (2\sqrt{7}) = 3 \cdot 2 \cdot \sqrt{5 \cdot 7} = 6\sqrt{35}
\]
Another example using binomials:
\[
(3 + \sqrt{2})(2 - \sqrt{5}) = 3 \cdot 2 + 3 \cdot (-\sqrt{5}) + \sqrt{2} \cdot 2 + \sqrt{2} \cdot (-\sqrt{5})
\]
Using the FOIL method (First, Outer, Inner, Last):
- First: \(3 \cdot 2 = 6\)
- Outer: \(3 \cdot -\sqrt{5} = -3\sqrt{5}\)
- Inner: \(\sqrt{2} \cdot 2 = 2\sqrt{2}\)
- Last: \(\sqrt{2} \cdot -\sqrt{5} = -\sqrt{10}\)
Combining these, we get:
\[
6 - 3\sqrt{5} + 2\sqrt{2} - \sqrt{10}
\]
Dividing Radical Expressions
When dividing radical expressions, we often need to rationalize the denominator. Here are the steps:
- If the denominator is a single term with a radical, multiply the numerator and the denominator by a radical that will eliminate the radical in the denominator.
- If the denominator is a binomial with a radical, multiply the numerator and the denominator by the conjugate of the denominator to rationalize it.
- Simplify the resulting expression if possible.
For example, to rationalize the denominator in \(\frac{3}{\sqrt{5}}\):
\[
\frac{3}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5}
\]
Another example with a binomial denominator:
\[
\frac{2}{3 + \sqrt{7}} \cdot \frac{3 - \sqrt{7}}{3 - \sqrt{7}} = \frac{2(3 - \sqrt{7})}{(3 + \sqrt{7})(3 - \sqrt{7})}
\]
Multiplying out the denominator using the difference of squares formula, we get:
\[
(3 + \sqrt{7})(3 - \sqrt{7}) = 3^2 - (\sqrt{7})^2 = 9 - 7 = 2
\]
So the expression simplifies to:
\[
\frac{2(3 - \sqrt{7})}{2} = 3 - \sqrt{7}
\]
This completes the process of multiplying and dividing radical expressions.
Special Cases: Perfect Squares and Cubes
Understanding perfect squares and perfect cubes can significantly simplify working with radicals and exponents. These special cases often allow for more straightforward calculations and can be used to recognize patterns in algebraic expressions.
Perfect Squares
A perfect square is the result of squaring an integer. The square root of a perfect square is always an integer. Here are some examples of perfect squares:
- \(1^2 = 1\)
- \(2^2 = 4\)
- \(3^2 = 9\)
- \(4^2 = 16\)
- \(5^2 = 25\)
- \(6^2 = 36\)
- \(7^2 = 49\)
- \(8^2 = 64\)
- \(9^2 = 81\)
- \(10^2 = 100\)
When simplifying square roots, recognizing perfect squares can help to quickly identify the root. For example, \(\sqrt{64} = 8\) because \(8^2 = 64\).
Perfect Cubes
Similarly, a perfect cube is the result of cubing an integer. The cube root of a perfect cube is always an integer. Here are some examples of perfect cubes:
- \(1^3 = 1\)
- \(2^3 = 8\)
- \(3^3 = 27\)
- \(4^3 = 64\)
- \(5^3 = 125\)
- \(6^3 = 216\)
- \(7^3 = 343\)
- \(8^3 = 512\)
- \(9^3 = 729\)
- \(10^3 = 1000\)
Recognizing perfect cubes helps in simplifying cube roots. For example, \(\sqrt[3]{125} = 5\) because \(5^3 = 125\).
Applications and Examples
Let's look at some practical examples of simplifying roots using perfect squares and cubes:
- Simplify \(\sqrt{144}\):
\(144\) is a perfect square since \(12^2 = 144\). Therefore, \(\sqrt{144} = 12\).
- Simplify \(\sqrt[3]{216}\):
\(216\) is a perfect cube since \(6^3 = 216\). Therefore, \(\sqrt[3]{216} = 6\).
In algebra, these simplifications can be crucial in solving equations and simplifying expressions involving radicals. By memorizing common perfect squares and cubes, you can quickly recognize and simplify these special cases.
Converting Between Radical and Exponent Notation
Understanding how to convert between radical and exponent notation is crucial for simplifying complex expressions. Below are detailed steps to guide you through the conversion process:
From Radical to Exponent Notation
Any radical expression can be written as an expression with a fractional exponent. The general form is:
- \(\sqrt[n]{a} = a^{\frac{1}{n}}\)
For example:
- \(\sqrt[4]{81} = 81^{\frac{1}{4}}\)
- \(\sqrt[3]{8} = 8^{\frac{1}{3}}\)
- \(\sqrt[5]{32} = 32^{\frac{1}{5}}\)
From Exponent to Radical Notation
Similarly, any expression with a rational exponent can be written in radical form. The general form is:
- \(a^{\frac{m}{n}} = \sqrt[n]{a^m}\)
For example:
- \(16^{\frac{1}{2}} = \sqrt{16}\)
- \(27^{\frac{2}{3}} = \sqrt[3]{27^2}\)
- \(64^{\frac{3}{4}} = \sqrt[4]{64^3}\)
Examples and Practice
Let’s look at a few more examples to solidify our understanding:
- Convert \( \sqrt[5]{243} \) to exponent notation:
- Solution: \( 243^{\frac{1}{5}} \)
- Convert \( 125^{\frac{2}{3}} \) to radical form:
- Solution: \( \sqrt[3]{125^2} \)
- Convert \( \sqrt[6]{64^3} \) to exponent notation:
- Solution: \( 64^{\frac{3}{6}} = 64^{\frac{1}{2}} \)
These conversions allow for flexibility in solving and simplifying algebraic expressions. Understanding both forms enables you to choose the most convenient method for the problem at hand.

Examples and Practice Problems
In this section, we will look at various examples and practice problems to help you master the technique of simplifying square roots using exponents. Follow the detailed steps below to solve each problem.
Example 1: Simplifying a Basic Square Root
Simplify \( \sqrt{50} \).
- Factor the number inside the square root: \( 50 = 25 \times 2 \).
- Rewrite using the property of square roots: \( \sqrt{50} = \sqrt{25 \times 2} \).
- Simplify the perfect square: \( \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \).
So, \( \sqrt{50} = 5\sqrt{2} \).
Example 2: Simplifying a Square Root with Variables
Simplify \( \sqrt{72x^4} \).
- Factor the number and variable inside the square root: \( 72x^4 = 36 \times 2 \times x^4 \).
- Rewrite using the property of square roots: \( \sqrt{72x^4} = \sqrt{36 \times 2 \times x^4} \).
- Simplify the perfect squares: \( \sqrt{36 \times 2 \times x^4} = \sqrt{36} \times \sqrt{2} \times \sqrt{x^4} = 6 \times \sqrt{2} \times x^2 \).
So, \( \sqrt{72x^4} = 6x^2\sqrt{2} \).
Example 3: Simplifying a Square Root with a Fraction
Simplify \( \sqrt{\frac{8}{50}} \).
- Factor the numerator and the denominator: \( \frac{8}{50} = \frac{4 \times 2}{25 \times 2} = \frac{4}{25} \).
- Rewrite using the quotient property of square roots: \( \sqrt{\frac{8}{50}} = \sqrt{\frac{4}{25}} \).
- Simplify the square roots: \( \sqrt{\frac{4}{25}} = \frac{\sqrt{4}}{\sqrt{25}} = \frac{2}{5} \).
So, \( \sqrt{\frac{8}{50}} = \frac{2}{5} \).
Practice Problems
- Simplify \( \sqrt{98} \).
- Simplify \( \sqrt{128x^6} \).
- Simplify \( \sqrt{\frac{45}{81}} \).
- Simplify \( \sqrt{\frac{32x^5}{64}} \).
- Simplify \( \sqrt{75y^8} \).
Try solving these problems on your own. Remember to look for perfect square factors and apply the properties of square roots and exponents.
Common Mistakes and How to Avoid Them
When simplifying square roots with exponents, it's important to be aware of common mistakes that can lead to incorrect results. Here are some of the most frequent errors and tips on how to avoid them:
1. Incorrectly Applying the Product Rule
The product rule states that \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\). A common mistake is to misapply this rule, especially when dealing with negative numbers or variables.
- Example: \(\sqrt{-4 \cdot 4} \neq \sqrt{-4} \cdot \sqrt{4}\)
- Correct Approach: Simplify inside the square root first, if possible.
- Tip: Always ensure that the values under the square root are non-negative unless dealing with complex numbers.
2. Misinterpreting the Power Rule
The power rule \((a^m)^n = a^{mn}\) is often incorrectly applied when simplifying expressions with exponents and radicals.
- Example: \((\sqrt{a})^2 \neq a\) without considering absolute values.
- Correct Approach: Use the property \((a^{1/2})^2 = |a|\).
- Tip: Remember that squaring a square root returns the absolute value of the original number.
3. Overlooking the Quotient Rule
The quotient rule for square roots states that \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\). Misapplying this can lead to incorrect simplifications.
- Example: \(\sqrt{\frac{4}{9}} \neq \frac{4}{9}\).
- Correct Approach: Simplify to \(\frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3}\).
- Tip: Simplify the numerator and denominator separately before applying the square root.
4. Forgetting Rational Exponents
Another common mistake is to forget how to handle rational exponents. For instance, \(a^{m/n} = \sqrt[n]{a^m}\).
- Example: \(a^{3/2} \neq \sqrt{a}^3\).
- Correct Approach: Rewrite \(a^{3/2}\) as \((a^3)^{1/2} = \sqrt{a^3}\).
- Tip: Break down the exponent into a multiplication of two terms.
5. Neglecting Negative Exponents
Negative exponents need careful handling. Remember \(a^{-n} = \frac{1}{a^n}\).
- Example: \(a^{-2} \neq -a^2\).
- Correct Approach: Rewrite \(a^{-2}\) as \(\frac{1}{a^2}\).
- Tip: Always convert negative exponents to positive by using the reciprocal.
6. Misapplying the Power of a Product Rule
This rule states \((ab)^n = a^n b^n\), and incorrect application can lead to errors.
- Example: \((2 \cdot 3)^2 \neq 2^2 \cdot 3^2\).
- Correct Approach: Simplify to \(6^2 = 36\) and separately \(2^2 \cdot 3^2 = 4 \cdot 9 = 36\).
- Tip: Apply the exponent to each factor individually.
By understanding these common mistakes and how to avoid them, you can ensure accurate simplification of square roots with exponents.
Advanced Techniques for Simplifying Radicals
Simplifying radicals can sometimes require more advanced techniques, especially when dealing with higher-order roots, variables, and complex expressions. Here, we will explore some advanced methods to simplify these types of radicals.
1. Using Rational Exponents
One effective method for simplifying radicals is to use rational exponents. This technique can make it easier to apply exponent rules and simplify the expression.
For example, let's simplify \( \sqrt[3]{x^5} \) using rational exponents:
- Rewrite the radical as an exponent: \( \sqrt[3]{x^5} = x^{5/3} \).
- Simplify the exponent if possible. Here, \( x^{5/3} \) is already in its simplest form.
2. Simplifying Complex Expressions
When dealing with complex expressions, break them down into simpler parts and simplify each part separately.
Example:
Simplify \( \sqrt[3]{40m^5} \):
- Factor the radicand: \( 40m^5 = 2^3 \cdot 5 \cdot m^3 \cdot m^2 \).
- Rewrite as separate radicals: \( \sqrt[3]{2^3 \cdot 5 \cdot m^3 \cdot m^2} = \sqrt[3]{2^3} \cdot \sqrt[3]{5} \cdot \sqrt[3]{m^3} \cdot \sqrt[3]{m^2} \).
- Simplify each radical: \( 2 \cdot \sqrt[3]{5} \cdot m \cdot \sqrt[3]{m^2} \).
- Combine the simplified parts: \( 2m \sqrt[3]{5m^2} \).
3. Applying the Quotient Rule
The quotient rule for radicals can be very helpful in simplifying expressions that involve division.
Example:
Simplify \( \frac{\sqrt{50}}{\sqrt{2}} \):
- Combine the radicals: \( \frac{\sqrt{50}}{\sqrt{2}} = \sqrt{\frac{50}{2}} \).
- Simplify the fraction: \( \sqrt{25} = 5 \).
4. Using Conjugates to Simplify Radicals
For expressions involving binomials with radicals, multiplying by the conjugate can help eliminate the radicals.
Example:
Simplify \( \frac{3}{\sqrt{2} + 1} \) by multiplying by the conjugate:
- Identify the conjugate: \( \sqrt{2} - 1 \).
- Multiply numerator and denominator by the conjugate: \( \frac{3}{\sqrt{2} + 1} \cdot \frac{\sqrt{2} - 1}{\sqrt{2} - 1} = \frac{3(\sqrt{2} - 1)}{(\sqrt{2} + 1)(\sqrt{2} - 1)} \).
- Simplify the denominator using the difference of squares: \( (\sqrt{2})^2 - (1)^2 = 2 - 1 = 1 \).
- Combine the results: \( 3(\sqrt{2} - 1) = 3\sqrt{2} - 3 \).
5. Simplifying Higher-Order Roots
For roots higher than square roots, such as cube roots, look for factors that are perfect cubes.
Example:
Simplify \( \sqrt[3]{-27x^4y^3} \):
- Factor the expression into cubes: \( \sqrt[3]{-1 \cdot 27 \cdot x^3 \cdot x \cdot y^3} \).
- Rewrite as separate radicals: \( \sqrt[3]{-1^3} \cdot \sqrt[3]{3^3} \cdot \sqrt[3]{x^3} \cdot \sqrt[3]{x} \cdot \sqrt[3]{y^3} \).
- Simplify each radical: \( -1 \cdot 3 \cdot x \cdot \sqrt[3]{x} \cdot y \).
- Combine the simplified parts: \( -3xy\sqrt[3]{x} \).
Practice Problems
- Simplify \( \sqrt[4]{81a^8b^{12}} \).
- Simplify \( \frac{\sqrt{75}}{\sqrt{3}} \).
- Simplify \( \sqrt[3]{16x^9y^4} \).
Using these advanced techniques will help you simplify a wide range of radical expressions, making complex problems more manageable.
Applications of Simplified Radicals
Simplified radicals have a variety of applications in different fields, including mathematics, physics, engineering, and computer science. Understanding how to simplify radicals can make complex calculations more manageable and can be particularly useful in solving real-world problems. Here are some key applications:
-
Geometry and Trigonometry:
Simplifying square roots is crucial in geometry, especially when dealing with the Pythagorean theorem. For example, in finding the length of the hypotenuse in a right triangle, you might need to simplify expressions like \( \sqrt{a^2 + b^2} \). Simplified radicals also appear in trigonometric calculations, such as finding exact values for sine, cosine, and tangent functions. -
Physics:
In physics, simplified radicals are often used in formulas involving kinetic and potential energy, wave functions, and electrical circuits. For instance, the formula for the period of a pendulum involves the square root of the length of the pendulum divided by the acceleration due to gravity: \( T = 2\pi \sqrt{\frac{L}{g}} \). -
Engineering:
Engineers frequently encounter simplified radicals in stress-strain relationships, fluid dynamics, and electrical engineering. Simplifying these expressions can make it easier to analyze and solve engineering problems. For example, the stress in a material under load might be expressed with a square root term that needs to be simplified for practical calculations. -
Computer Science:
Algorithms involving distance calculations, such as those used in computer graphics and machine learning, often require the use of simplified radicals. The Euclidean distance formula, \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \), is a common example where simplification helps in optimizing the computation. -
Finance:
In finance, simplified radicals can appear in the calculation of standard deviations and other statistical measures. Simplifying these expressions aids in more accurate and easier interpretation of financial data.
Mastering the simplification of radicals not only aids in academic pursuits but also provides practical tools for various professional fields. By breaking down complex expressions into simpler forms, professionals can improve their problem-solving efficiency and accuracy.

Summary and Key Takeaways
Simplifying square roots and understanding exponents is a foundational mathematical skill with numerous applications. Here are the key takeaways from our comprehensive guide:
-
Basics of Simplifying Square Roots:
To simplify square roots, find the largest square factor of the radicand. For example, to simplify \( \sqrt{50} \), recognize that 50 can be factored into \( 25 \times 2 \), thus \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \).
-
Understanding Rational Exponents:
Rational exponents are another way to represent roots. For instance, \( a^{\frac{1}{n}} \) is equivalent to \( \sqrt[n]{a} \). This notation is useful in algebraic manipulations and solving equations.
-
Simplifying Radicals with Variables:
When variables are involved, apply the same principles. For example, \( \sqrt{x^4} = x^2 \) assuming \( x \) is non-negative. When variables have exponents, split them into squares whenever possible.
-
Using the Quotient Property:
The quotient property \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) helps simplify complex expressions. For example, \( \sqrt{\frac{50}{2}} = \sqrt{25} = 5 \).
-
Operations with Radical Expressions:
Add or subtract radicals by combining like terms, and multiply or divide using the properties of exponents. For instance, \( \sqrt{a} \cdot \sqrt{b} = \sqrt{ab} \) and \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \).
-
Perfect Squares and Cubes:
Recognize perfect squares and cubes to simplify radicals efficiently. For example, \( \sqrt{36} = 6 \) and \( \sqrt[3]{27} = 3 \).
-
Converting Between Notations:
Switch between radical notation and exponent notation as needed. For example, \( \sqrt[3]{x} = x^{\frac{1}{3}} \). This is useful in solving equations and performing algebraic operations.
-
Real-world Applications:
Simplifying radicals is useful in various fields such as physics for solving problems involving distances and speeds, in engineering for calculating areas and volumes, and in finance for computing interest rates and growth factors.
-
Common Mistakes:
Avoid common errors like incorrectly combining unlike radicals or forgetting to apply the absolute value in certain cases. Always check your work for accuracy.
-
Practice and Mastery:
Consistent practice with a variety of problems is key to mastering these concepts. Work through examples and solve practice problems to build confidence and proficiency.
Understanding and simplifying square roots, especially when combined with exponents, equips you with the tools to tackle more advanced mathematical concepts and practical problems effectively.
Video hướng dẫn cách đơn giản hóa căn bậc với biến số, số mũ, phân số và căn bậc ba. Học cách xử lý các biểu thức phức tạp trong đại số một cách hiệu quả.
Đơn Giản Hóa Căn Bậc Với Biến Số, Số Mũ, Phân Số, Căn Bậc Ba - Đại Số
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai của số chính phương và số mũ. Khám phá các phương pháp hiệu quả để xử lý các biểu thức toán học phức tạp.
Đơn Giản Hóa Căn Bậc Hai của Số Chính Phương và Số Mũ