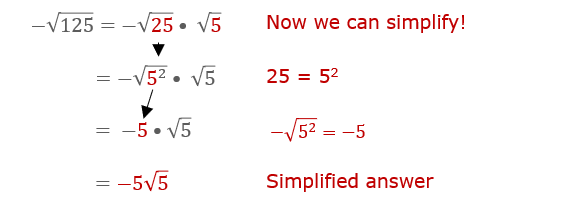Topic how to simplify expressions with square roots: Learning how to simplify expressions with square roots is essential for mastering algebra and beyond. This guide will take you through the process step-by-step, providing clear explanations and practical examples to help you understand and apply these techniques effectively.
Table of Content
- How to Simplify Expressions with Square Roots
- Introduction to Square Roots
- Understanding Square Roots
- Properties of Square Roots
- Methods to Simplify Square Roots
- Simplifying Perfect Squares
- Factoring Inside the Radical
- Using Prime Factorization
- Simplifying Expressions with Multiple Radicals
- Working with Variables in Square Roots
- Common Mistakes to Avoid
- Examples and Practice Problems
- Advanced Simplification Techniques
- Conclusion
- YOUTUBE: Hướng dẫn cách đơn giản hóa biểu thức căn bậc hai với biến.
How to Simplify Expressions with Square Roots
Simplifying expressions with square roots involves reducing the expression to its simplest form. Here are the steps to simplify square root expressions:
1. Prime Factorization
First, perform prime factorization on the number under the square root. This means breaking down the number into its prime factors.
- Example: \( \sqrt{75} \)
- 75 can be factored into \( 3 \times 5 \times 5 \)
2. Pair the Prime Factors
Next, pair the prime factors. For each pair of the same number, you can move one number out of the square root.
- Example: \( \sqrt{75} = \sqrt{3 \times 5 \times 5} \)
- We have one pair of 5's.
3. Simplify
Move the paired number outside the square root and multiply any numbers left inside the square root.
- Example: \( \sqrt{75} = 5\sqrt{3} \)
Examples
Here are a few more examples to illustrate the process:
| \( \sqrt{50} \) | \( = \sqrt{2 \times 5 \times 5} = 5\sqrt{2} \) |
| \( \sqrt{45} \) | \( = \sqrt{3 \times 3 \times 5} = 3\sqrt{5} \) |
| \( \sqrt{18} \) | \( = \sqrt{2 \times 3 \times 3} = 3\sqrt{2} \) |
Frequently Asked Questions (FAQs)
-
Q: Can all square roots be simplified?
A: No, not all square roots can be simplified. Only those that have factors which can be paired.
-
Q: What if there are no pairs of factors?
A: If there are no pairs, the square root remains in its original form. For example, \( \sqrt{3} \) cannot be simplified further.
-
Q: Can you simplify square roots with variables?
A: Yes, the same rules apply. For example, \( \sqrt{x^2 \times y} = x\sqrt{y} \) if \( x \) and \( y \) are positive.

READ MORE:
Introduction to Square Roots
Square roots are mathematical operations that help us find the original value which was squared to obtain a given number. Understanding square roots is fundamental for simplifying expressions involving radicals.
The square root of a number a is a value x such that:
\( x^2 = a \)
For example:
- \( \sqrt{4} = 2 \) because \( 2^2 = 4 \)
- \( \sqrt{9} = 3 \) because \( 3^2 = 9 \)
- \( \sqrt{16} = 4 \) because \( 4^2 = 16 \)
Square roots can be represented using the radical symbol \( \sqrt{} \). The number under the radical symbol is called the radicand. If the radicand is a perfect square (like 4, 9, or 16), the square root is an integer. However, not all numbers are perfect squares, and their square roots are irrational numbers. For instance, \( \sqrt{2} \) and \( \sqrt{3} \) cannot be simplified to exact integers and are instead left in their radical form.
Here is a step-by-step approach to understanding and working with square roots:
- Identify the radicand: The number or expression under the square root symbol.
- Determine if the radicand is a perfect square: If so, find the integer square root.
- If the radicand is not a perfect square, use methods such as prime factorization to simplify the square root.
For example, to simplify \( \sqrt{12} \):
- Factor 12 into prime factors: \( 12 = 2^2 \times 3 \).
- Apply the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \): \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \).
Understanding these fundamental concepts will allow you to simplify expressions involving square roots more effectively. In the following sections, we will delve deeper into the properties of square roots and various methods to simplify them.
Understanding Square Roots
Square roots are fundamental in mathematics, representing a value that, when multiplied by itself, gives the original number. The square root of a number \( n \) is written as \( \sqrt{n} \). For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
Here are key concepts and properties to understand:
- Every positive number has two square roots: one positive and one negative. For instance, both \( 5 \) and \( -5 \) are square roots of \( 25 \).
- The positive square root is known as the principal square root and is denoted by the radical symbol \( \sqrt{} \). The negative square root is written as \( -\sqrt{} \).
- The square root of zero is zero: \( \sqrt{0} = 0 \).
- Square roots are the inverse operations of squaring. If \( n^2 = m \), then \( \sqrt{m} = n \).
Let's look at some examples:
- Simplifying \( \sqrt{144} \):
Since \( 12^2 = 144 \), we have \( \sqrt{144} = 12 \).
- Simplifying \( -\sqrt{289} \):
Since \( 17^2 = 289 \), we get \( -\sqrt{289} = -17 \).
When simplifying expressions involving square roots, follow these steps:
- Simplify inside the radical: Evaluate any arithmetic under the radical sign first.
- Combine like terms: If there are multiple square root terms, combine them if possible.
- Simplify the radical: Find the square root of any perfect squares.
For example:
Simplify \( \sqrt{25} + \sqrt{144} \):
- First, find the square roots: \( \sqrt{25} = 5 \) and \( \sqrt{144} = 12 \).
- Then, add the results: \( 5 + 12 = 17 \).
Simplify \( \sqrt{25 + 144} \):
- Add under the radical first: \( 25 + 144 = 169 \).
- Then, find the square root: \( \sqrt{169} = 13 \).
Understanding these properties and steps will help in simplifying expressions with square roots more effectively. Practice with various examples to gain confidence and proficiency.
Properties of Square Roots
The properties of square roots are essential to understand when simplifying expressions involving square roots. Here are some fundamental properties:
- Non-Negativity: The square root of a non-negative number is always non-negative. For any real number \(a \geq 0\), \(\sqrt{a} \geq 0\).
- Product Property: The square root of a product is the product of the square roots. For any non-negative real numbers \(a\) and \(b\), \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\).
- Quotient Property: The square root of a quotient is the quotient of the square roots. For any non-negative real numbers \(a\) and \(b\) (with \(b \neq 0\)), \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- Square of a Square Root: The square of a square root returns the original number. For any non-negative real number \(a\), \((\sqrt{a})^2 = a\).
- Radical Expressions with Variables: When dealing with variables, the same properties apply, assuming the variables represent non-negative values. For example, \(\sqrt{x^2} = x\) for \(x \geq 0\).
Here are a few examples to illustrate these properties:
- Example 1: Simplify \(\sqrt{36} \times \sqrt{25}\)
- Using the product property: \(\sqrt{36 \cdot 25} = \sqrt{900} = 30\)
- Alternatively: \(\sqrt{36} = 6\) and \(\sqrt{25} = 5\), so \(6 \times 5 = 30\)
- Example 2: Simplify \(\sqrt{\frac{49}{16}}\)
- Using the quotient property: \(\frac{\sqrt{49}}{\sqrt{16}} = \frac{7}{4}\)
- So, \(\sqrt{\frac{49}{16}} = \frac{7}{4}\)
- Example 3: Simplify \((\sqrt{81})^2\)
- Using the square of a square root property: \((\sqrt{81})^2 = 81\)
- Example 4: Simplify \(\sqrt{16x^2}\) where \(x \geq 0\)
- Using the properties of radicals with variables: \(\sqrt{16x^2} = \sqrt{16} \cdot \sqrt{x^2} = 4x\)
These properties are foundational for simplifying more complex expressions involving square roots. Mastering them will make it easier to handle various algebraic problems.
Methods to Simplify Square Roots
Simplifying square roots involves several methods that help break down complex radical expressions into simpler forms. Here, we will explore some common techniques used to simplify square roots:
1. Factoring Inside the Radical
One of the simplest methods to simplify square roots is by factoring the number inside the radical into its prime factors. Then, pairs of prime factors can be taken out of the radical.
- Find the prime factorization of the number under the radical.
- Identify pairs of prime factors.
- Move each pair of prime factors out of the radical as a single number.
- Multiply the numbers outside the radical to get the simplified form.
Example:
\(\sqrt{72}\)
Prime factorization of 72 is \(2^3 \cdot 3^2\).
Pairs: \( (2^2) \cdot (3^2) \cdot 2 \)
Simplified: \( 2 \cdot 3 \cdot \sqrt{2} = 6\sqrt{2} \)
2. Using the Property of Square Roots
The property of square roots states that the square root of a product is equal to the product of the square roots. This property can be utilized to simplify expressions with square roots.
Formula: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
Example:
\(\sqrt{50}\)
Split into factors: \(\sqrt{25 \cdot 2}\)
Simplified: \(\sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\)
3. Simplifying Expressions with Variables
When simplifying square roots that contain variables, follow the same process as with numbers, treating the variables as factors.
- Factor the expression under the radical.
- Apply the square root to each factor separately.
- Combine the results.
Example:
\(\sqrt{18x^2y}\)
Factor: \(\sqrt{9 \cdot 2 \cdot x^2 \cdot y}\)
Simplified: \(\sqrt{9} \cdot \sqrt{2} \cdot \sqrt{x^2} \cdot \sqrt{y} = 3x\sqrt{2y}\)
4. Rationalizing the Denominator
When a square root appears in the denominator, we can rationalize the denominator by multiplying the numerator and the denominator by the radical in the denominator.
- Identify the radical in the denominator.
- Multiply the numerator and the denominator by that radical.
- Simplify the expression.
Example:
\(\frac{5}{\sqrt{3}}\)
Rationalize: \(\frac{5}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}\)
5. Combining Like Terms
When simplifying expressions that contain multiple square roots, look for like terms that can be combined.
- Identify like terms under the radicals.
- Combine like terms.
- Simplify the result.
Example:
\(2\sqrt{5} + 3\sqrt{5} - \sqrt{5}\)
Combine like terms: \((2 + 3 - 1)\sqrt{5} = 4\sqrt{5}\)

Simplifying Perfect Squares
Simplifying perfect squares involves recognizing when a number under the square root (the radicand) is a perfect square. A perfect square is a number that can be expressed as the product of an integer with itself. Here are the steps to simplify perfect squares:
-
Identify Perfect Squares: Look for numbers that are perfect squares. Some examples of perfect squares are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, etc. For example:
- \(4 = 2^2\)
- \(9 = 3^2\)
- \(16 = 4^2\)
-
Apply the Square Root: Use the property that the square root of a perfect square is an integer. For example:
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
-
Simplify the Expression: If the radicand is a perfect square, simplify the expression by taking the square root. For example:
- \(\sqrt{25} = 5\)
- \(\sqrt{36} = 6\)
- \(\sqrt{49} = 7\)
Here are a few more examples to illustrate simplifying perfect squares:
- \(\sqrt{64} = 8\)
- \(\sqrt{81} = 9\)
- \(\sqrt{100} = 10\)
By understanding and recognizing perfect squares, you can quickly and easily simplify square root expressions.
Factoring Inside the Radical
Simplifying square roots by factoring inside the radical involves breaking down the number into its prime factors and then applying the property of square roots that allows us to split the radical into the product of separate square roots. Here is a step-by-step guide on how to do this:
-
Identify Factors: Begin by identifying the factors of the number inside the square root. For example, to simplify √72, we start by breaking it down into its prime factors:
72 = 2 × 2 × 2 × 3 × 3
-
Pair the Factors: Group the factors into pairs of identical numbers:
72 = (2 × 2) × (2) × (3 × 3)
-
Simplify the Square Root: Apply the square root to each pair and single out the pairs from the square root:
√72 = √(2² × 2 × 3²)
√72 = √(2²) × √(2) × √(3²)
Since the square root of a square is the number itself, we get:
√72 = 2 × √(2) × 3
Combine the constants:
√72 = 6√2
-
Write the Simplified Form: The simplified form of √72 is:
6√2
Here are more examples to practice:
- Example 1: Simplify √18
- Example 2: Simplify √50
- Example 3: Simplify √128
18 = 2 × 3 × 3
√18 = √(3² × 2) = 3√2
50 = 2 × 5 × 5
√50 = √(5² × 2) = 5√2
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
√128 = √(2⁶ × 2) = 2³√2 = 8√2
By understanding how to factor inside the radical, you can simplify square roots more easily and accurately. This technique is particularly useful for dealing with more complex expressions and ensuring your answers are in their simplest form.
Using Prime Factorization
To simplify square roots, especially when dealing with complex expressions, using prime factorization is a powerful technique. Here's a step-by-step method:
- Identify the square roots in the expression.
- Apply prime factorization to each number inside the square root.
- Express each square root as a product of prime factors.
- Combine like terms under the same square root symbol.
- If possible, simplify the expression further by taking out any perfect squares from the square root.
- Repeat the process until the expression is in its simplest form.
Let's illustrate this with an example:
| Example: | \(\sqrt{50}\) |
| Step 1: | \( \sqrt{50} = \sqrt{2 \times 25} \) |
| Step 2: | \( \sqrt{2 \times 25} = \sqrt{2 \times 5^2} \) |
| Step 3: | \( \sqrt{2 \times 5^2} = 5\sqrt{2} \) |
Therefore, \( \sqrt{50} = 5\sqrt{2} \).
Using prime factorization not only simplifies square roots but also helps in understanding the factors contributing to the original expression.
Simplifying Expressions with Multiple Radicals
When simplifying expressions containing multiple square roots, follow these steps for clarity and accuracy:
- Identify and separate each square root in the expression.
- Apply simplification techniques like combining like terms under the same square root.
- If possible, rationalize denominators to eliminate square roots from denominators.
- Use algebraic techniques such as factoring or completing the square to simplify further.
- Verify the solution by ensuring all operations are correctly applied.
Let's illustrate this with an example:
| Example: | \(\sqrt{18} + \sqrt{8}\) |
| Step 1: | \(\sqrt{18} + \sqrt{8} = \sqrt{9 \times 2} + \sqrt{4 \times 2}\) |
| Step 2: | \(\sqrt{9 \times 2} + \sqrt{4 \times 2} = 3\sqrt{2} + 2\sqrt{2}\) |
| Step 3: | \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\) |
Therefore, \(\sqrt{18} + \sqrt{8} = 5\sqrt{2}\).
By following these steps, you can effectively simplify expressions with multiple radicals, ensuring accuracy and clarity in your mathematical calculations.

Working with Variables in Square Roots
When dealing with variables inside square roots, follow these steps to simplify expressions:
- Identify variables under square roots in the expression.
- Factor out any perfect squares from under the square root.
- Combine like terms under the same square root.
- Rationalize denominators if necessary.
- Verify the solution by substituting back into the original expression.
Let's illustrate this with an example:
| Example: | \(\sqrt{18x^2} + \sqrt{8x}\) |
| Step 1: | \(\sqrt{18x^2} + \sqrt{8x} = \sqrt{9 \cdot 2 \cdot x^2} + \sqrt{4 \cdot 2 \cdot x}\) |
| Step 2: | \(\sqrt{9 \cdot 2 \cdot x^2} + \sqrt{4 \cdot 2 \cdot x} = 3x\sqrt{2} + 2\sqrt{2x}\) |
| Step 3: | \(3x\sqrt{2} + 2\sqrt{2x}\) (simplified form) |
Therefore, \(\sqrt{18x^2} + \sqrt{8x} = 3x\sqrt{2} + 2\sqrt{2x}\).
By following these steps, you can effectively work with variables inside square roots, simplifying expressions while maintaining accuracy.
Common Mistakes to Avoid
When simplifying expressions with square roots, watch out for these common mistakes:
- Incorrect Application of Rules: Misapplying rules such as distributing square roots over addition or subtraction.
- Ignoring Simplification Opportunities: Failing to simplify perfect squares or common factors under square roots.
- Forgetting to Rationalize: Leaving square roots in denominators without rationalizing.
- Mixing Terms Incorrectly: Combining terms with different radicals or variables improperly.
- Skipping Verification: Not verifying the final solution by substituting back into the original expression.
Avoiding these mistakes ensures accurate and clear simplification of expressions involving square roots.
Examples and Practice Problems
Here are some examples and practice problems to reinforce your understanding of simplifying expressions with square roots:
-
Simplify \( \sqrt{50} \).
Step 1: \( \sqrt{50} = \sqrt{2 \times 25} \) Step 2: \( \sqrt{2 \times 25} = \sqrt{2 \times 5^2} \) Step 3: \( \sqrt{2 \times 5^2} = 5\sqrt{2} \) Therefore, \( \sqrt{50} = 5\sqrt{2} \).
-
Simplify \( \sqrt{18} + \sqrt{8} \).
Step 1: \( \sqrt{18} + \sqrt{8} = \sqrt{9 \times 2} + \sqrt{4 \times 2} \) Step 2: \( \sqrt{9 \times 2} + \sqrt{4 \times 2} = 3\sqrt{2} + 2\sqrt{2} \) Step 3: \( 3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2} \) (simplified form) Therefore, \( \sqrt{18} + \sqrt{8} = 5\sqrt{2} \).
-
Simplify \( \sqrt{18x^2} + \sqrt{8x} \).
Step 1: \( \sqrt{18x^2} + \sqrt{8x} = 3x\sqrt{2} + 2\sqrt{2x} \) Step 2: \( 3x\sqrt{2} + 2\sqrt{2x} \) (simplified form) Therefore, \( \sqrt{18x^2} + \sqrt{8x} = 3x\sqrt{2} + 2\sqrt{2x} \).
Practice these examples to improve your skills in simplifying expressions with square roots.
Advanced Simplification Techniques
For more complex expressions involving square roots, consider these advanced techniques:
- Using Conjugates: Rationalize denominators by multiplying the numerator and denominator by the conjugate of the denominator.
- Completing the Square: Transform quadratic expressions into perfect square trinomials to simplify square roots.
- Factoring and Simplifying: Factorize expressions under square roots to identify and simplify common factors.
- Substitution: Substitute variables or expressions to simplify complex square roots into more manageable forms.
- Verification: Always verify solutions by substituting back into the original expression to ensure accuracy.
Let's demonstrate one of these techniques:
| Example: | Rationalize \( \frac{\sqrt{3}}{\sqrt{3} + 2} \) |
| Step 1: | Multiply numerator and denominator by the conjugate of the denominator: \( \frac{\sqrt{3}(\sqrt{3} - 2)}{(\sqrt{3} + 2)(\sqrt{3} - 2)} \) |
| Step 2: | Denominator simplifies to \( 3 - 4 = -1 \), so \( \frac{\sqrt{3}(\sqrt{3} - 2)}{-1} = -\sqrt{3} + 2\sqrt{3} \) |
Therefore, \( \frac{\sqrt{3}}{\sqrt{3} + 2} = -\sqrt{3} + 2 \).
These advanced techniques empower you to tackle even the most intricate expressions involving square roots with confidence.

Conclusion
Simplifying expressions with square roots requires understanding fundamental rules and applying systematic techniques. By following structured steps like identifying perfect squares, using prime factorization, and rationalizing denominators, you can efficiently simplify even complex expressions. Avoiding common mistakes such as misapplying rules or skipping verification ensures accuracy in your calculations.
Practice is key to mastering these skills. Through examples and practice problems, you can strengthen your ability to simplify expressions with confidence. Remember to verify solutions by substituting back into the original expression to confirm correctness.
With these tools and techniques, you are well-equipped to handle various scenarios involving square roots, enabling clearer and more precise mathematical solutions.
Hướng dẫn cách đơn giản hóa biểu thức căn bậc hai với biến.
Đơn giản hóa biểu thức căn bậc hai với biến
READ MORE:
Hướng dẫn đơn giản hóa biểu thức căn bậc hai với biến, số mũ, phân số, và căn bậc ba trong đại số.
Đơn giản hóa căn bậc hai với biến, số mũ, phân số, căn bậc ba - Đại số