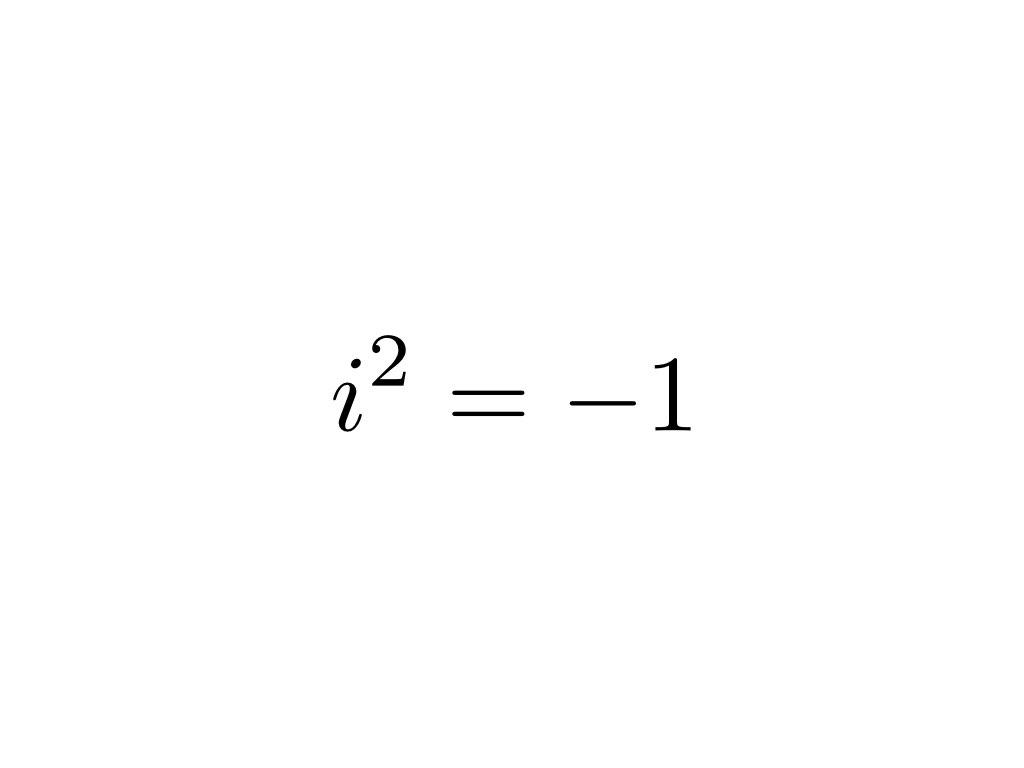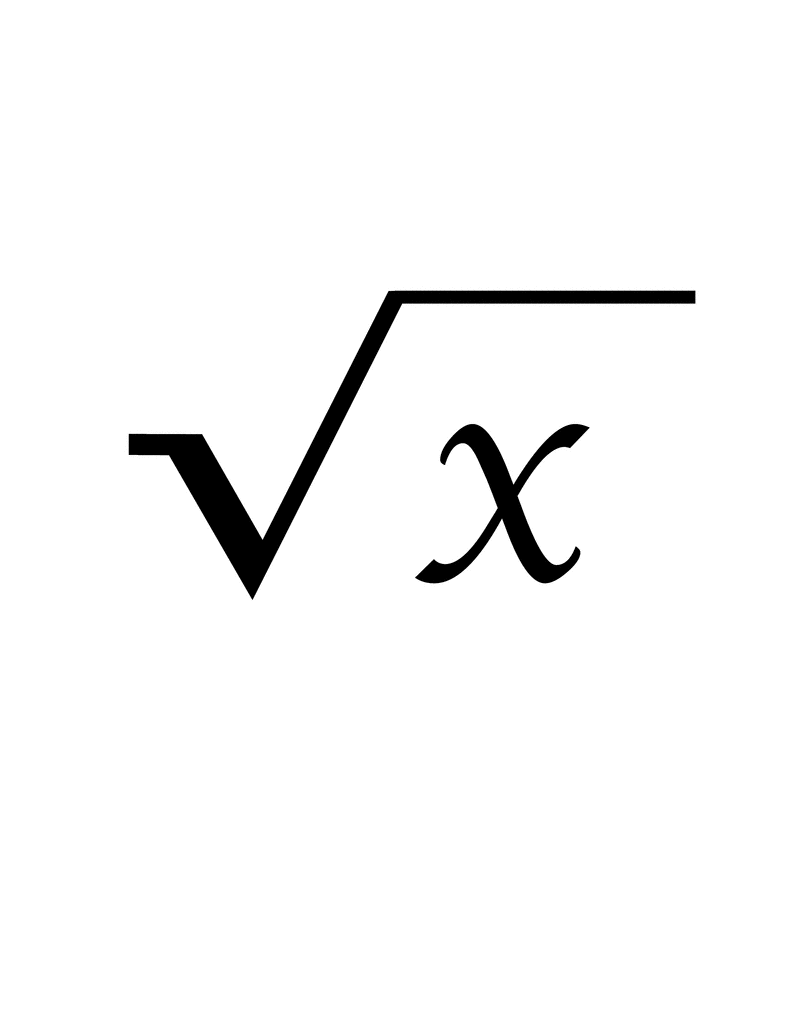Topic is square root the same as 1/2 power: Discover the intriguing connection between square roots and the 1/2 power in mathematics. This article explores how the square root of a number is fundamentally related to raising that number to the power of 1/2, providing clarity and insight into their equivalence and applications in various mathematical contexts.
Table of Content
- Understanding the Relationship Between Square Roots and Exponents
- Introduction to Square Roots and Exponents
- Definition and Basics
- Relationship Between Square Roots and Exponents
- Calculating Square Roots and Exponents
- Principal Square Root vs. Negative Square Root
- Properties of Exponents
- Multiplying and Dividing Exponents
- Exponents with Negative Bases
- Simplifying Expressions Involving Square Roots
- Practical Applications of Square Roots and Exponents
- Historical Context and Development
- YOUTUBE: Xem video này để hiểu tại sao 'x mũ nửa' có nghĩa là căn bậc hai và liệu video này có phù hợp với bài viết với từ khóa 'is square root the same as 1/2 power'?
Understanding the Relationship Between Square Roots and Exponents
When working with square roots and exponents, it's important to understand their relationship. Specifically, the square root of a number is equivalent to raising that number to the power of 1/2.
Mathematical Explanation
Let's explore this concept mathematically:
- If we take the square root of a number \(x\), it is written as \(\sqrt{x}\).
- This can also be expressed as \(x^{1/2}\).
Why is this true? Consider the following steps:
- By definition, \(\sqrt{x} \cdot \sqrt{x} = x\).
- We can rewrite this using exponents as \((x^{1/2})^2 = x\).
- Applying the power rule \((a^m)^n = a^{m \cdot n}\), we get \(x^{1/2 \cdot 2} = x\).
- Simplifying the exponent, we find \(x^1 = x\), which confirms that \(x^{1/2} = \sqrt{x}\).
Properties of Exponents and Roots
| Expression | Equivalent Form |
|---|---|
| \(\sqrt{a}\) | \(a^{1/2}\) |
| \(\sqrt[3]{a}\) (cube root) | \(a^{1/3}\) |
| \(\sqrt[n]{a}\) (nth root) | \(a^{1/n}\) |
This equivalence is fundamental in algebra and calculus, allowing for flexible manipulation of expressions involving roots and exponents.
Examples
Let's look at some practical examples:
- \(\sqrt{9} = 9^{1/2} = 3\)
- \(\sqrt{16} = 16^{1/2} = 4\)
- \(\sqrt{25} = 25^{1/2} = 5\)
These examples illustrate how taking the square root of a number is equivalent to raising it to the power of 1/2.
Conclusion
Understanding that the square root of a number \(x\) is the same as raising \(x\) to the power of 1/2 is crucial for solving various mathematical problems. This relationship simplifies complex calculations and enhances our ability to work with different forms of expressions in algebra.

READ MORE:
Introduction to Square Roots and Exponents
Square roots and exponents are fundamental concepts in mathematics that play a crucial role in various mathematical operations and real-world applications.
Square roots are used to find a number which, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. In mathematical notation, this is written as:
\(\sqrt{9} = 3\)
Exponents, on the other hand, are used to express repeated multiplication of a number by itself. For example, \(2^3\) (read as "two to the power of three" or "two cubed") is equal to 2 multiplied by itself three times, which equals 8. In general, \(a^n\) represents 'a' multiplied by itself 'n' times.
The relationship between square roots and exponents is significant. Specifically, the square root of a number can be represented as an exponent. The square root of a number 'a' is the same as raising 'a' to the power of 1/2. This can be written as:
\(\sqrt{a} = a^{1/2}\)
To illustrate, consider the number 16. The square root of 16 is 4 because 4 multiplied by itself gives 16. Using exponents, we can express this as:
\(\sqrt{16} = 16^{1/2} = 4\)
Here is a comparison table to understand better:
| Expression | Result |
|---|---|
| \(\sqrt{25}\) | 5 |
| 25^{1/2} | 5 |
| \(\sqrt{36}\) | 6 |
| 36^{1/2} | 6 |
Understanding these concepts is vital as they form the basis for more complex mathematical operations and are applied in fields such as physics, engineering, and computer science. Mastery of square roots and exponents will enhance your mathematical skills and problem-solving abilities.
Definition and Basics
Understanding square roots and exponents is fundamental to mathematics. Let's break down these concepts step by step.
Square Roots:
The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). This can be represented as:
\[
\sqrt{x} = x^{\frac{1}{2}}
\]
For example, the square root of 9 is 3 because \( 3 \times 3 = 9 \).
Exponents:
Exponents are a way to represent repeated multiplication of a number by itself. The expression \( a^n \) means that \( a \) is multiplied by itself \( n \) times. Here are some key rules:
- Any number raised to the power of 1 is itself: \( a^1 = a \).
- Any number raised to the power of 0 is 1: \( a^0 = 1 \).
- Multiplying exponents with the same base: \( a^m \times a^n = a^{m+n} \).
- Dividing exponents with the same base: \( \frac{a^m}{a^n} = a^{m-n} \).
- Raising a power to another power: \( (a^m)^n = a^{m \times n} \).
- Product raised to a power: \( (ab)^n = a^n \times b^n \).
- Quotient raised to a power: \( \left(\frac{a}{b}\right)^n = \frac{a^n}{b^n} \).
Relationship Between Square Roots and Exponents:
Square roots are essentially the same as raising a number to the power of \( \frac{1}{2} \). For example:
\[
\sqrt{16} = 16^{\frac{1}{2}} = 4
\]
This relationship helps in simplifying expressions and solving equations involving square roots and exponents.
Examples:
Let's look at some examples to clarify these concepts:
- \( 4^2 = 16 \), so \( \sqrt{16} = 4 \).
- \( 2^3 = 8 \), so \( \sqrt[3]{8} = 2 \), where \( \sqrt[3]{x} \) denotes the cube root of \( x \).
- \( 5^4 = 625 \), so \( \sqrt[4]{625} = 5 \), where \( \sqrt[4]{x} \) denotes the fourth root of \( x \).
These fundamental definitions and relationships form the basis for more advanced topics in algebra and calculus.
Relationship Between Square Roots and Exponents
The relationship between square roots and exponents is a fundamental concept in mathematics. A square root of a number \(a\) is a value that, when multiplied by itself, gives \(a\). This can be expressed using exponents as follows:
For any positive number \(a\), the square root of \(a\) is equivalent to raising \(a\) to the power of \(\frac{1}{2}\). This is written mathematically as:
\[
\sqrt{a} = a^{\frac{1}{2}}
\]
This notation helps in understanding and simplifying various mathematical expressions and equations. The exponent \(\frac{1}{2}\) signifies the operation of taking the square root. For example:
- \(\sqrt{9} = 9^{\frac{1}{2}} = 3\)
- \(\sqrt{16} = 16^{\frac{1}{2}} = 4\)
The properties of exponents apply to the square root operation as well. Here are a few key properties:
- Multiplying Exponents: When multiplying numbers with the same base, you add the exponents. For example, \[ a^{\frac{1}{2}} \times a^{\frac{1}{2}} = a^{\frac{1}{2} + \frac{1}{2}} = a^{1} = a \]
- Dividing Exponents: When dividing numbers with the same base, you subtract the exponents. For example, \[ \frac{a^{1}}{a^{\frac{1}{2}}} = a^{1 - \frac{1}{2}} = a^{\frac{1}{2}} \]
- Raising a Power to a Power: When raising a power to another power, you multiply the exponents. For example, \[ (a^{\frac{1}{2}})^{2} = a^{\frac{1}{2} \times 2} = a^{1} = a \]
These properties show the consistency and utility of using exponent notation for square roots. Understanding this relationship simplifies many aspects of algebra and calculus.
Calculating Square Roots and Exponents
Calculating square roots and exponents is fundamental in understanding the relationship between these two concepts. Here is a detailed guide to help you with the calculations:
Calculating Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example:
- \(\sqrt{9} = 3\) because \(3 \times 3 = 9\).
- \(\sqrt{16} = 4\) because \(4 \times 4 = 16\).
In general, for any positive number \(a\), the square root of \(a\) is denoted as \(\sqrt{a}\).
Calculating Exponents
Exponents are a way to express repeated multiplication of a number by itself. For example:
- \(2^3 = 2 \times 2 \times 2 = 8\).
- \(5^4 = 5 \times 5 \times 5 \times 5 = 625\).
Here, \(2\) and \(5\) are bases, and \(3\) and \(4\) are exponents.
Relationship Between Square Roots and Exponents
Square roots and exponents are closely related. Specifically, the square root of a number is the same as raising that number to the power of \(1/2\). For example:
- \(\sqrt{9} = 9^{1/2} = 3\).
- \(\sqrt{16} = 16^{1/2} = 4\).
This relationship can be generalized for any positive number \(a\) as follows:
\[\sqrt{a} = a^{1/2}\]
Examples of Calculating Exponents
- \(4^2 = 4 \times 4 = 16\)
- \(3^3 = 3 \times 3 \times 3 = 27\)
- \(2^{1/2} = \sqrt{2} \approx 1.414\)
- \(27^{1/3} = \sqrt[3]{27} = 3\)
Combining Exponents and Roots
Sometimes, you might need to combine exponents and roots in a single expression. For example:
- \(8^{2/3} = (\sqrt[3]{8})^2 = 2^2 = 4\)
- \(16^{3/4} = (\sqrt[4]{16})^3 = 2^3 = 8\)
Practice Problems
- Calculate \(9^{1/2}\).
- Calculate \(2^5\).
- Find the value of \(125^{1/3}\).
- Simplify \(32^{3/5}\).
By understanding these calculations, you can see the clear relationship between square roots and exponents, enhancing your mathematical skills.
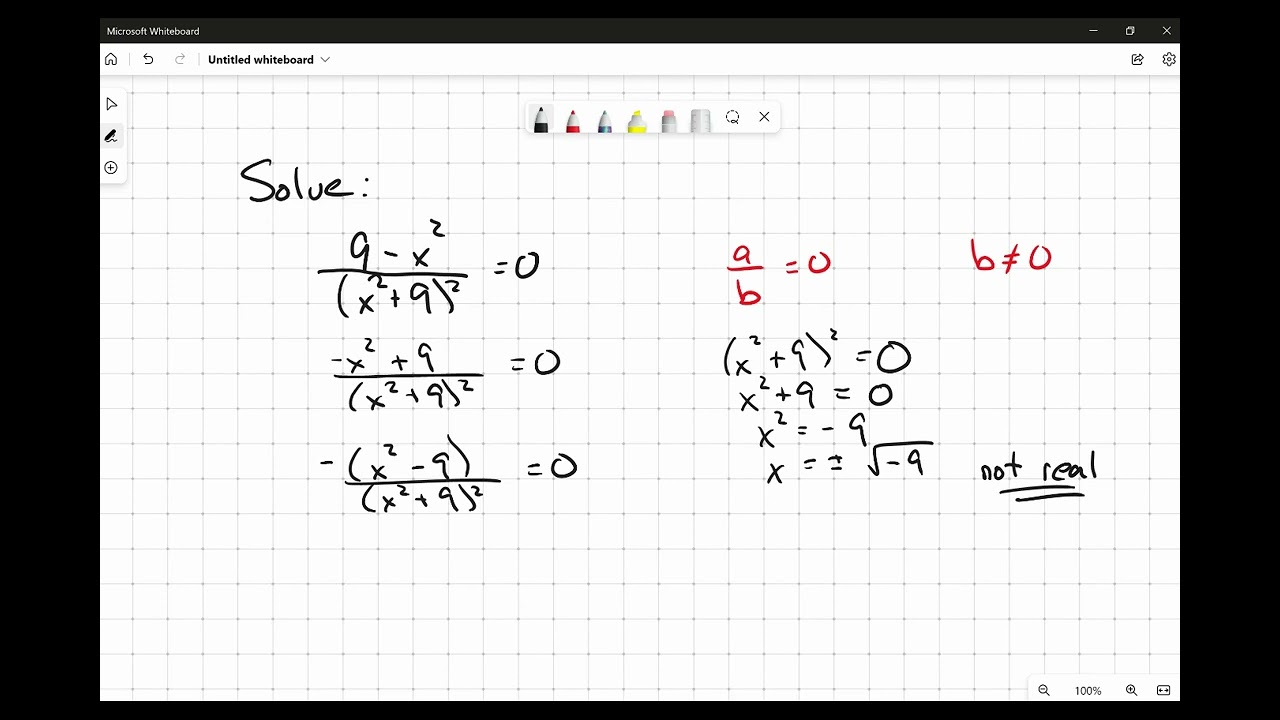
Principal Square Root vs. Negative Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. Square roots can be both positive and negative because both positive and negative values, when squared, yield a positive result. However, when we refer to the square root, we often mean the principal (or positive) square root.
For any non-negative real number \( a \), the principal square root of \( a \) is denoted as \( \sqrt{a} \) and is always non-negative. The negative square root of \( a \) is denoted as \( -\sqrt{a} \). Mathematically, this can be expressed as:
\[
\sqrt{a} = b \quad \text{where} \quad b \geq 0 \quad \text{and} \quad b^2 = a
\]
\[
-\sqrt{a} = c \quad \text{where} \quad c \leq 0 \quad \text{and} \quad c^2 = a
\]
Understanding the Principal Square Root
The principal square root is the non-negative root of a non-negative number. It is the most commonly used square root in mathematics and is represented without a sign.
- For example, the principal square root of 9 is 3 because \( 3 \times 3 = 9 \).
- We denote this as \( \sqrt{9} = 3 \).
Understanding the Negative Square Root
The negative square root is simply the negative of the principal square root. It is less commonly used in elementary mathematics but important in solving quadratic equations.
- For example, the negative square root of 9 is -3 because \( -3 \times -3 = 9 \).
- We denote this as \( -\sqrt{9} = -3 \).
Square Roots in Equations
When solving equations involving square roots, it's important to consider both the principal and negative roots. For instance, solving \( x^2 = 9 \) yields two solutions:
- \( x = \sqrt{9} = 3 \)
- \( x = -\sqrt{9} = -3 \)
Visual Representation
To better understand the concept, consider the graph of the function \( y = \sqrt{x} \) and \( y = -\sqrt{x} \). The principal square root \( \sqrt{x} \) corresponds to the upper half of the parabola, while the negative square root \( -\sqrt{x} \) corresponds to the lower half.
The following table summarizes the principal and negative square roots for several values:
| Value | Principal Square Root | Negative Square Root |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | -1 |
| 4 | 2 | -2 |
| 9 | 3 | -3 |
| 16 | 4 | -4 |
Properties of Exponents
Exponents are a fundamental concept in mathematics that describe how many times a number, known as the base, is multiplied by itself. Understanding the properties of exponents is essential for simplifying expressions and solving equations involving exponential terms.
- Product of Powers: When multiplying two expressions with the same base, add the exponents.
\[a^m \times a^n = a^{m+n}\]
Example: \[2^3 \times 2^4 = 2^{3+4} = 2^7 = 128\]
- Quotient of Powers: When dividing two expressions with the same base, subtract the exponents.
\[\frac{a^m}{a^n} = a^{m-n}\]
Example: \[\frac{5^6}{5^2} = 5^{6-2} = 5^4 = 625\]
- Power of a Power: When raising an exponent to another exponent, multiply the exponents.
\[(a^m)^n = a^{m \times n}\]
Example: \[(3^2)^3 = 3^{2 \times 3} = 3^6 = 729\]
- Power of a Product: When raising a product to an exponent, raise each factor in the product to the exponent.
\[(ab)^n = a^n \times b^n\]
Example: \[(2 \times 3)^4 = 2^4 \times 3^4 = 16 \times 81 = 1296\]
- Power of a Quotient: When raising a quotient to an exponent, raise both the numerator and the denominator to the exponent.
\[\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}\]
Example: \[\left(\frac{2}{3}\right)^3 = \frac{2^3}{3^3} = \frac{8}{27}\]
- Zero Exponent: Any non-zero base raised to the power of zero is 1.
\[a^0 = 1\]
Example: \[7^0 = 1\]
- Negative Exponent: A negative exponent indicates the reciprocal of the base raised to the absolute value of the exponent.
\[a^{-n} = \frac{1}{a^n}\]
Example: \[4^{-2} = \frac{1}{4^2} = \frac{1}{16}\]
- Fractional Exponent: A fractional exponent represents a root of the base. Specifically, \(a^{\frac{1}{n}}\) is the n-th root of \(a\).
\[a^{\frac{1}{n}} = \sqrt[n]{a}\]
Example: \[16^{\frac{1}{4}} = \sqrt[4]{16} = 2\]
For more complex fractions, such as \(a^{\frac{m}{n}}\), it can be interpreted as taking the n-th root of the base raised to the power of m.
\[a^{\frac{m}{n}} = \sqrt[n]{a^m} = (\sqrt[n]{a})^m\]
Example: \[8^{\frac{2}{3}} = \sqrt[3]{8^2} = \sqrt[3]{64} = 4\]
These properties are essential for simplifying and manipulating expressions involving exponents. They provide a framework for understanding more advanced mathematical concepts and solving exponential equations.
Multiplying and Dividing Exponents
When working with exponents, there are specific properties and rules that simplify the process of multiplication and division. Understanding these rules helps in solving more complex mathematical problems involving exponents.
Multiplying Exponents with the Same Base
To multiply exponents with the same base, you simply add the exponents. Mathematically, this can be represented as:
\[ a^m \times a^n = a^{m+n} \]
For example:
\[ 4^3 \times 4^5 = 4^{3+5} = 4^8 \]
This simplifies to:
\[ 4^3 \times 4^5 = 4 \times 4 \times 4 \times 4 \times 4 \times 4 \times 4 \times 4 = 65,536 \]
Dividing Exponents with the Same Base
When dividing exponents with the same base, you subtract the exponent of the denominator from the exponent of the numerator. This can be expressed as:
\[ \frac{a^m}{a^n} = a^{m-n} \]
For example:
\[ \frac{3^6}{3^2} = 3^{6-2} = 3^4 \]
This simplifies to:
\[ \frac{3^6}{3^2} = \frac{3 \times 3 \times 3 \times 3 \times 3 \times 3}{3 \times 3} = 3 \times 3 \times 3 \times 3 = 81 \]
Multiplying and Dividing Exponents with Different Bases
When dealing with different bases, the multiplication and division are handled separately:
\[ (a \times b)^n = a^n \times b^n \]
\[ \left(\frac{a}{b}\right)^n = \frac{a^n}{b^n} \]
For example:
\[ (2 \times 3)^4 = 2^4 \times 3^4 = 16 \times 81 = 1296 \]
\[ \left(\frac{4}{2}\right)^3 = \frac{4^3}{2^3} = \frac{64}{8} = 8 \]
Raising a Power to a Power
When an exponent is raised to another exponent, you multiply the exponents. This is expressed as:
\[ (a^m)^n = a^{m \times n} \]
For example:
\[ (3^2)^3 = 3^{2 \times 3} = 3^6 = 729 \]
Fractional Exponents
Fractional exponents denote roots. For instance, the square root of a number is expressed as raising the number to the power of one-half:
\[ a^{1/2} = \sqrt{a} \]
Similarly, the cube root is expressed as:
\[ a^{1/3} = \sqrt[3]{a} \]
For example:
\[ 9^{1/2} = \sqrt{9} = 3 \]
\[ 27^{1/3} = \sqrt[3]{27} = 3 \]
These properties simplify complex calculations and help in understanding the behavior of exponents in various mathematical contexts.
Exponents with Negative Bases
Working with exponents that have negative bases can be intriguing due to the unique behaviors that arise. Here's a detailed look at the properties and rules associated with exponents having negative bases:
1. Even and Odd Powers:
- Even Exponents: When a negative base is raised to an even exponent, the result is positive. This is because multiplying a negative number an even number of times cancels out the negative signs.
- Example: \((-3)^2 = (-3) \times (-3) = 9\)
- Odd Exponents: When a negative base is raised to an odd exponent, the result is negative. This is due to the presence of an odd number of negative signs.
- Example: \((-3)^3 = (-3) \times (-3) \times (-3) = -27\)
2. Fractional Exponents:
When dealing with negative bases and fractional exponents, the situation becomes more complex:
- If the denominator of the fractional exponent is even, the base must be positive to have a real number result.
- Example: \((-16)^{1/2}\) is not a real number because the square root of a negative number is not defined in the set of real numbers.
- If the denominator is odd, then a negative base is allowed.
- Example: \((-27)^{1/3} = -3\), since \(-3 \times -3 \times -3 = -27\)
3. Combining Exponents:
- Multiplying: When multiplying expressions with the same negative base, the exponents are added.
- Example: \((-2)^3 \times (-2)^4 = (-2)^{3+4} = (-2)^7 = -128\)
- Dividing: When dividing expressions with the same negative base, the exponents are subtracted.
- Example: \(\frac{(-5)^6}{(-5)^2} = (-5)^{6-2} = (-5)^4 = 625\)
- Power of a Power: When raising a power to another power, the exponents are multiplied.
- Example: \(\left((-3)^2\right)^3 = (-3)^{2 \times 3} = (-3)^6 = 729\)
4. Summary of Key Points:
| Operation | Rule | Example |
|---|---|---|
| Multiplying Same Base | \((-a)^m \times (-a)^n = (-a)^{m+n}\) | \((-2)^3 \times (-2)^2 = (-2)^5 = -32\) |
| Dividing Same Base | \(\frac{(-a)^m}{(-a)^n} = (-a)^{m-n}\) | \(\frac{(-4)^5}{(-4)^2} = (-4)^3 = -64\) |
| Power of a Power | \(\left((-a)^m\right)^n = (-a)^{m \times n}\) | \(\left((-3)^2\right)^3 = (-3)^6 = 729\) |
Understanding these rules can help in simplifying and solving expressions involving exponents with negative bases effectively.

Simplifying Expressions Involving Square Roots
Simplifying expressions involving square roots often requires understanding the relationship between exponents and roots. Here are the steps to simplify these expressions:
-
Identify Perfect Squares: Look for perfect square factors in the radicand (the number inside the square root).
For example, in \(\sqrt{50}\), the number 50 can be factored into \(25 \times 2\), where 25 is a perfect square.
-
Apply the Square Root Property: Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) to split the square root into simpler parts.
Continuing the example, \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\).
-
Simplify the Expression: Simplify the resulting square roots. If possible, express them in their simplest form.
-
Combine Like Terms: If you have multiple square roots, combine like terms to simplify the expression further.
For example, \(3\sqrt{2} + 4\sqrt{2} = 7\sqrt{2}\).
Let's see more examples to understand better:
-
Example 1: Simplify \(\sqrt{72}\).
Solution: Factor 72 into \(36 \times 2\). Then, \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\).
-
Example 2: Simplify \(\sqrt{200}\).
Solution: Factor 200 into \(100 \times 2\). Then, \(\sqrt{200} = \sqrt{100} \times \sqrt{2} = 10\sqrt{2}\).
Another important concept is understanding the relationship between exponents and square roots. The square root of a number is the same as raising that number to the power of 1/2. This can be written as:
\[\sqrt{a} = a^{1/2}\]
Using this property, you can also simplify expressions involving exponents:
-
Example 3: Simplify \((16)^{3/2}\).
Solution: Rewrite the expression using the exponent property: \((16)^{3/2} = (16^{1/2})^3 = (4)^3 = 64\).
By understanding these steps and properties, simplifying expressions involving square roots becomes more manageable.
Practical Applications of Square Roots and Exponents
Square roots and exponents have a wide range of practical applications in various fields, including science, engineering, finance, and everyday life. Understanding these concepts can help solve real-world problems effectively. Below are some key applications:
-
Engineering and Physics:
Square roots are often used in engineering to calculate distances and magnitudes. For example, the Pythagorean theorem involves square roots to determine the length of the hypotenuse in a right triangle:
\[
c = \sqrt{a^2 + b^2}
\]
where \(c\) is the hypotenuse, and \(a\) and \(b\) are the other two sides.Exponents are used in physics to describe exponential growth or decay, such as radioactive decay or population growth, which can be modeled by:
\[
N(t) = N_0 e^{kt}
\]
where \(N(t)\) is the quantity at time \(t\), \(N_0\) is the initial quantity, \(e\) is the base of natural logarithms, and \(k\) is the growth or decay constant. -
Finance:
In finance, exponents are crucial for calculating compound interest, which can be expressed as:
\[
A = P \left(1 + \frac{r}{n}\right)^{nt}
\]
where \(A\) is the amount of money accumulated after \(n\) years, including interest, \(P\) is the principal amount, \(r\) is the annual interest rate, and \(n\) is the number of times interest is compounded per year. -
Statistics and Probability:
Square roots are used to calculate standard deviation, a measure of the dispersion of a set of values:
\[
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}
\]
where \(\sigma\) is the standard deviation, \(N\) is the number of values, \(x_i\) is each individual value, and \(\mu\) is the mean of the values. -
Computer Science:
In algorithms, exponents and square roots are used to describe the time complexity of algorithms. For example, the time complexity of the binary search algorithm is \(O(\log n)\), indicating a logarithmic relationship between the input size and the number of operations required.
-
Everyday Life:
Square roots and exponents appear in daily tasks such as cooking, where doubling a recipe might involve squaring quantities, or in sound levels, where the decibel scale is logarithmic, indicating the power of sound intensity.
Understanding these practical applications helps to see the value of mastering square roots and exponents in various contexts, enhancing problem-solving skills and analytical thinking.
Historical Context and Development
In the historical development of mathematics, the concept of square roots and exponents has evolved significantly. One notable historical question that arises is whether the square root is equivalent to raising a number to the power of \( \frac{1}{2} \).
To understand this, historically, the notion of square roots predates the formal use of exponents as we know them today. Early mathematicians primarily dealt with square roots as a means to find numbers that, when multiplied by themselves, yielded a given number. This concept gradually evolved alongside algebraic notation and the formalization of mathematical operations.
It wasn't until the development of algebraic notation and the introduction of exponents that the equivalence between square roots and fractional exponents became clearer. In modern mathematics, particularly in algebra and calculus, the expression \( x^{1/2} \) indeed represents the square root of \( x \).
This historical journey underscores the iterative nature of mathematical discovery, where concepts like exponents and square roots evolved and interlinked over time, contributing to the broader framework of mathematical understanding we have today.
Xem video này để hiểu tại sao 'x mũ nửa' có nghĩa là căn bậc hai và liệu video này có phù hợp với bài viết với từ khóa 'is square root the same as 1/2 power'?
Video: Tại sao "x mũ nửa" có nghĩa là căn bậc hai?
READ MORE:
Xem video này để tìm hiểu tại sao căn bậc hai tương đương với một nửa lũy thừa và xem liệu video này có phù hợp với bài viết với từ khóa 'is square root the same as 1/2 power'?
Video: Tại sao căn bậc hai là một nửa lũy thừa?