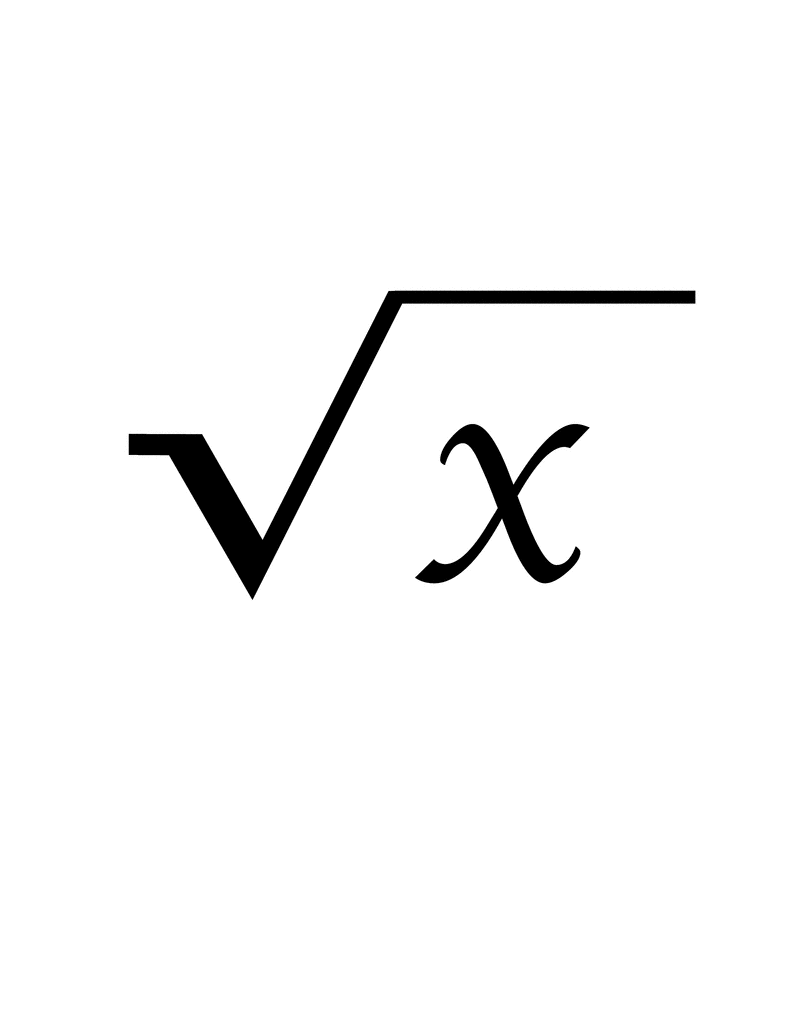Topic 1/2 / square root 3/2: Understanding how to simplify the expression 1/2 divided by the square root of 3/2 can be crucial for algebra and trigonometry problems. This article will guide you through the steps of simplifying such expressions, ensuring a solid grasp of the underlying concepts and their applications in various mathematical contexts.
Table of Content
Simplifying the Expression
The mathematical expression to simplify is:
\(\frac{1/2}{\sqrt{3}/2}\)
Steps to Simplify
- Multiply the numerator by the reciprocal of the denominator:
- \(\frac{1/2}{\sqrt{3}/2} = \frac{1/2} \times \frac{2}{\sqrt{3}}\)
- Multiply the fractions:
- \(\frac{1 \times 2}{2 \times \sqrt{3}} = \frac{2}{2\sqrt{3}}\)
- Cancel the common factor of 2:
- \(\frac{2}{2\sqrt{3}} = \frac{1}{\sqrt{3}}\)
- Rationalize the denominator:
- \(\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}\)
Result
The simplified form of the expression is:
\(\frac{\sqrt{3}}{3}\)
Additional Information
This process involves multiplying by the reciprocal of the denominator, simplifying the fraction, and rationalizing the denominator to ensure there are no radicals in the denominator. This is a common technique in algebra to simplify expressions involving square roots.
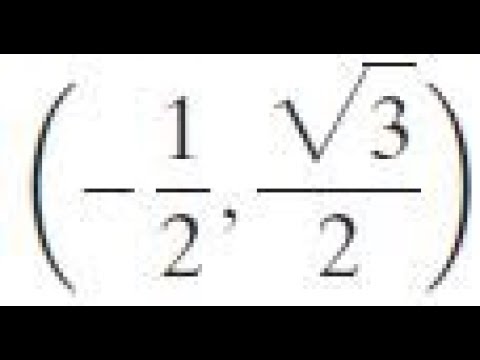
READ MORE:
Introduction
The expression \( \frac{1/2}{\sqrt{3}/2} \) can be simplified through a series of algebraic steps. This operation involves dividing fractions, which can be tackled by multiplying by the reciprocal of the denominator. Understanding this process provides insights into algebraic manipulation and the properties of square roots.
- Start with the expression \( \frac{1/2}{\sqrt{3}/2} \).
- Multiply the numerator by the reciprocal of the denominator: \( \frac{1/2} \times \frac{2}{\sqrt{3}} \).
- Simplify the expression by canceling common factors: \( \frac{1 \times 2}{2 \times \sqrt{3}} = \frac{1}{\sqrt{3}} \).
- Rationalize the denominator by multiplying both numerator and denominator by \( \sqrt{3} \): \( \frac{1 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{3} \).
This simplification shows the final form of the expression is \( \frac{\sqrt{3}}{3} \). Each step is crucial in understanding how to handle square roots and fractions effectively.
Basic Mathematical Concepts
Understanding how to simplify the expression \(\frac{1/2}{\sqrt{3}/2}\) involves several fundamental mathematical principles. Here, we will break down the steps involved in this process.
- Reciprocal of the Denominator
First, we convert the division into multiplication by using the reciprocal of the denominator:
\[
\frac{1/2}{\sqrt{3}/2} = \frac{1/2} \times \frac{2}{\sqrt{3}}
\] - Multiplication
Next, we multiply the numerators and the denominators:
\[
\frac{1 \times 2}{2 \times \sqrt{3}} = \frac{2}{2\sqrt{3}}
\] - Canceling Common Factors
We then cancel the common factor of 2 in the numerator and the denominator:
\[
\frac{2}{2\sqrt{3}} = \frac{1}{\sqrt{3}}
\] - Rationalizing the Denominator
To rationalize the denominator, we multiply the numerator and the denominator by \(\sqrt{3}\):
\[
\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\]
Thus, the simplified form of \(\frac{1/2}{\sqrt{3}/2}\) is \(\frac{\sqrt{3}}{3}\). This process demonstrates key algebraic techniques including reciprocal, multiplication, canceling common factors, and rationalizing the denominator.
Step-by-Step Simplification Process
The simplification of the expression \(\frac{1/2}{\sqrt{3}/2}\) involves several steps. Follow this detailed process to achieve the simplified form:
-
Multiply by the Reciprocal:
First, change the division of fractions into multiplication by the reciprocal of the denominator.
\[\frac{1/2}{\sqrt{3}/2} = \frac{1/2} \times \frac{2}{\sqrt{3}} = \frac{1 \times 2}{2 \times \sqrt{3}} = \frac{2}{2\sqrt{3}}\]
-
Simplify the Fraction:
Cancel the common factor in the numerator and the denominator.
\[\frac{2}{2\sqrt{3}} = \frac{1}{\sqrt{3}}\]
-
Rationalize the Denominator:
To rationalize the denominator, multiply both the numerator and the denominator by the square root of 3.
\[\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}\]
Thus, the simplified form of \(\frac{1/2}{\sqrt{3}/2}\) is \(\frac{\sqrt{3}}{3}\).
Common Mistakes and Tips
When simplifying the expression \(\frac{1/2}{\sqrt{3}/2}\), students often encounter common mistakes. Here are the most frequent errors and tips to avoid them:
- Incorrect Reciprocal: A common mistake is to incorrectly take the reciprocal of the denominator. Always remember that the reciprocal of \(\frac{\sqrt{3}}{2}\) is \(\frac{2}{\sqrt{3}}\).
- Forgetting to Simplify: After multiplying by the reciprocal, students may forget to simplify the fraction completely. Ensure all steps are followed through to reduce the expression to its simplest form.
- Not Rationalizing the Denominator: It is important to rationalize the denominator by multiplying both the numerator and denominator by the square root value to eliminate the radical from the denominator.
- Skipping Steps: Skipping steps can lead to errors. Follow a step-by-step approach to ensure accuracy.
Here are the correct steps to simplify the expression \(\frac{1/2}{\sqrt{3}/2}\):
- Multiply by the reciprocal: \(\frac{1/2} \times \frac{2}{\sqrt{3}} = \frac{1 \times 2}{2 \times \sqrt{3}} = \frac{2}{2\sqrt{3}}\).
- Simplify the fraction: \(\frac{2}{2\sqrt{3}} = \frac{1}{\sqrt{3}}\).
- Rationalize the denominator: Multiply by \(\frac{\sqrt{3}}{\sqrt{3}}\) to get \(\frac{1 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{3}\).
By following these steps carefully, you can simplify the expression correctly and avoid common pitfalls.
Applications in Trigonometry
The ratio \( \frac{1/2}{\sqrt{3}/2} \) simplifies to \( \frac{1}{\sqrt{3}} \) or \( \frac{\sqrt{3}}{3} \). This ratio has significant applications in trigonometry, especially when dealing with right triangles and the unit circle.
- In a 30-60-90 triangle, the sides are in the ratio \( 1 : \sqrt{3} : 2 \). Here, \( \frac{1/2}{\sqrt{3}/2} \) represents the tangent of 30°.
- In the unit circle, the coordinates of the point at an angle \( \theta \) from the positive x-axis are \( (\cos \theta, \sin \theta) \). For \( \theta = 30^\circ \), \( \cos 30^\circ = \frac{\sqrt{3}}{2} \) and \( \sin 30^\circ = \frac{1}{2} \), making the tangent \( \frac{1/2}{\sqrt{3}/2} \).
- This ratio also appears in trigonometric identities, such as the tangent addition and subtraction formulas, aiding in simplifying complex expressions.
Understanding these fundamental trigonometric ratios is crucial for solving problems involving angles and side lengths in various fields such as physics, engineering, and architecture.
Advanced Topics
Understanding the expression \(\frac{1}{2} / \sqrt{\frac{3}{2}}\) can be essential for delving into advanced mathematical concepts. This section explores how this simplification is applied in various higher-level math topics, including algebraic manipulations and calculus.
-
Rationalizing the Denominator: When simplifying expressions like \(\frac{1}{2} / \sqrt{\frac{3}{2}}\), it's crucial to rationalize the denominator. This involves multiplying both the numerator and the denominator by the conjugate of the denominator to eliminate the radical.
-
Integration Techniques: Such expressions often appear in integration problems where radicals need simplification for easier integration. Techniques like substitution or integration by parts might be used after rationalizing the denominator.
-
Differential Equations: In solving differential equations, particularly those involving radicals, simplifying such fractions is a critical step. This allows for the equations to be more manageable and solvable using standard methods.
-
Complex Numbers: Understanding the simplification of fractions involving square roots is also useful when dealing with complex numbers, where radicals are common in both polar and rectangular forms.
In summary, mastering the simplification of \(\frac{1}{2} / \sqrt{\frac{3}{2}}\) not only aids in basic algebra but also in various advanced mathematical disciplines. This fundamental skill is essential for tackling more complex problems and is widely applicable across different fields of mathematics.
Conclusion
In this guide, we have explored the step-by-step simplification process of the expression \( \frac{1/2}{\sqrt{3}/2} \). By breaking down each mathematical concept and method, we've ensured a thorough understanding of the principles involved.
Key takeaways include:
- Understanding the fundamental properties of fractions and radicals.
- Mastering the reciprocal of a fraction to simplify complex expressions.
- Applying square roots and their properties in various mathematical contexts.
- Following a structured approach to simplify the denominator and overall expression.
We also covered common mistakes and provided useful tips to avoid them, which will help in accurately simplifying similar mathematical expressions in the future. Furthermore, we discussed the relevance of these concepts in trigonometry, highlighting how radicals are used in trigonometric functions and unit circle calculations.
By rationalizing the denominator and dealing with complex fractions, you have gained advanced skills that are essential for higher-level mathematics. These techniques not only simplify calculations but also enhance problem-solving efficiency.
Ultimately, the ability to simplify expressions like \( \frac{1/2}{\sqrt{3}/2} \) is crucial for a solid foundation in mathematics. The knowledge and skills acquired here will be valuable in various applications, from academic pursuits to practical problem-solving scenarios.
Continue practicing these methods and exploring their applications to build confidence and proficiency in mathematical simplification and beyond.
Rationalize the Denominator 1/2 + Căn Bậc Hai 3
READ MORE:
Tại Sao "x Mũ Một Phần Hai" Nghĩa Là Căn Bậc Hai?