Topic how to simplify a negative square root: Learn how to simplify a negative square root with ease in this comprehensive guide. Discover step-by-step instructions, practical examples, and advanced techniques to master this essential mathematical concept. Perfect for students, educators, and anyone looking to enhance their understanding of imaginary numbers.
Table of Content
- How to Simplify a Negative Square Root
- Introduction to Negative Square Roots
- Understanding Imaginary Numbers
- Basic Steps to Simplify a Negative Square Root
- Examples of Simplifying Negative Square Roots
- Simplifying Negative Square Roots of Non-Perfect Squares
- Handling Negative Square Roots in Fractions
- Practical Applications of Imaginary Numbers
- Common Mistakes and How to Avoid Them
- Advanced Techniques in Simplifying Complex Expressions
- Conclusion and Summary
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai âm bằng cách sử dụng đơn vị ảo i, ví dụ với sqrt(-24).
How to Simplify a Negative Square Root
In mathematics, dealing with the square root of a negative number involves the concept of imaginary numbers. The square root of a negative number can be simplified using the imaginary unit \(i\), where \(i = \sqrt{-1}\). Here's a step-by-step guide to simplify a negative square root:
Step-by-Step Guide
Identify the negative square root to be simplified. For example, let's consider \(\sqrt{-36}\).
Express the negative square root in terms of \(i\). Since \(\sqrt{-1} = i\), we can write \(\sqrt{-36}\) as \(\sqrt{36 \cdot -1}\).
Separate the expression into the product of two square roots: \(\sqrt{36} \cdot \sqrt{-1}\).
Simplify the square roots: \(\sqrt{36} = 6\) and \(\sqrt{-1} = i\). Thus, \(\sqrt{36} \cdot \sqrt{-1} = 6i\).
Combine the results to obtain the simplified form: \(\sqrt{-36} = 6i\).
Example Problems
Example 1: Simplify \(\sqrt{-49}\)
Solution: \(\sqrt{-49} = \sqrt{49 \cdot -1} = \sqrt{49} \cdot \sqrt{-1} = 7i\)
Example 2: Simplify \(\sqrt{-100}\)
Solution: \(\sqrt{-100} = \sqrt{100 \cdot -1} = \sqrt{100} \cdot \sqrt{-1} = 10i\)
Special Cases
When the negative number is not a perfect square, simplify as much as possible. For example, \(\sqrt{-8} = \sqrt{8 \cdot -1} = \sqrt{8} \cdot \sqrt{-1} = 2\sqrt{2} \cdot i = 2i\sqrt{2}\).
If the number inside the square root is negative and a fraction, simplify the numerator and the denominator separately. For example, \(\sqrt{-\frac{4}{9}} = \frac{\sqrt{-4}}{\sqrt{9}} = \frac{2i}{3} = \frac{2i}{3}\).

READ MORE:
Introduction to Negative Square Roots
Understanding how to simplify a negative square root is a crucial aspect of algebra and complex numbers. When faced with the square root of a negative number, the concept of imaginary numbers becomes essential. The imaginary unit \(i\) is defined as \(i = \sqrt{-1}\), which allows us to simplify square roots of negative numbers.
Here are the basic steps to simplify a negative square root:
Identify the negative square root to be simplified. For example, consider \(\sqrt{-16}\).
Express the negative square root in terms of \(i\). Since \(\sqrt{-1} = i\), we can write \(\sqrt{-16}\) as \(\sqrt{16 \cdot -1}\).
Separate the expression into the product of two square roots: \(\sqrt{16} \cdot \sqrt{-1}\).
Simplify the square roots: \(\sqrt{16} = 4\) and \(\sqrt{-1} = i\). Thus, \(\sqrt{16} \cdot \sqrt{-1} = 4i\).
Combine the results to obtain the simplified form: \(\sqrt{-16} = 4i\).
This method can be applied to any negative square root, enabling the expression of the result in terms of \(i\).
Understanding the principles behind negative square roots and imaginary numbers is foundational for more advanced mathematical concepts, including complex numbers and their applications in various fields.
Understanding Imaginary Numbers
Imaginary numbers are a fundamental concept in mathematics, especially when dealing with the square roots of negative numbers. The imaginary unit is denoted by \(i\) and is defined as the square root of -1, or \(i = \sqrt{-1}\). This definition allows us to extend the real number system to include solutions to equations that do not have real solutions.
Here are the basic steps to understand and work with imaginary numbers:
Recognize the need for imaginary numbers: When we encounter the square root of a negative number, such as \(\sqrt{-9}\), we cannot find a real number that satisfies this condition since the square of any real number is always positive.
Introduce the imaginary unit \(i\): By defining \(i = \sqrt{-1}\), we can now express the square root of negative numbers in terms of \(i\). For example, \(\sqrt{-9} = \sqrt{9 \cdot -1} = \sqrt{9} \cdot \sqrt{-1} = 3i\).
Combine real and imaginary parts: Numbers that include both a real and an imaginary part are called complex numbers, and are written in the form \(a + bi\), where \(a\) and \(b\) are real numbers. For example, \(3 + 4i\) is a complex number.
Perform arithmetic with imaginary numbers: You can add, subtract, multiply, and divide complex numbers just as you do with real numbers, while keeping in mind that \(i^2 = -1\). For example:
Addition: \((2 + 3i) + (1 + 4i) = 3 + 7i\)
Multiplication: \((2 + 3i) \cdot (1 + 4i) = 2 + 8i + 3i + 12i^2 = 2 + 11i - 12 = -10 + 11i\)
Understanding imaginary numbers and how they work is crucial for solving equations involving the square roots of negative numbers and for delving deeper into complex numbers and their applications in fields such as engineering, physics, and advanced mathematics.
Basic Steps to Simplify a Negative Square Root
Simplifying a negative square root involves understanding the role of the imaginary unit \(i\), where \(i = \sqrt{-1}\). Here is a detailed step-by-step process to simplify a negative square root:
Identify the negative square root to be simplified. For instance, let's take \(\sqrt{-25}\).
Express the negative square root in terms of the imaginary unit \(i\). Since \(\sqrt{-1} = i\), we can rewrite \(\sqrt{-25}\) as \(\sqrt{25 \cdot -1}\).
Separate the expression into the product of two square roots: \(\sqrt{25} \cdot \sqrt{-1}\).
Simplify each square root individually. For \(\sqrt{25}\), the result is 5, and for \(\sqrt{-1}\), the result is \(i\). Thus, we have \(5 \cdot i\).
Combine the simplified results to obtain the final form: \(\sqrt{-25} = 5i\).
Let's look at more examples to solidify the process:
Example 1: Simplify \(\sqrt{-64}\)
Solution: \(\sqrt{-64} = \sqrt{64 \cdot -1} = \sqrt{64} \cdot \sqrt{-1} = 8i\)
Example 2: Simplify \(\sqrt{-81}\)
Solution: \(\sqrt{-81} = \sqrt{81 \cdot -1} = \sqrt{81} \cdot \sqrt{-1} = 9i\)
By following these steps, you can simplify any negative square root and express it in terms of the imaginary unit \(i\), making it easier to work with in further mathematical operations.
Examples of Simplifying Negative Square Roots
To gain a better understanding of simplifying negative square roots, let's look at a series of examples that illustrate the process step-by-step.
Example 1: Simplifying \(\sqrt{-49}\)
Identify the negative square root: \(\sqrt{-49}\).
Express it in terms of \(i\): \(\sqrt{-49} = \sqrt{49 \cdot -1}\).
Separate the square roots: \(\sqrt{49} \cdot \sqrt{-1}\).
Simplify the individual square roots: \(\sqrt{49} = 7\) and \(\sqrt{-1} = i\).
Combine the results: \(7 \cdot i = 7i\).
Thus, \(\sqrt{-49} = 7i\).
Example 2: Simplifying \(\sqrt{-100}\)
Identify the negative square root: \(\sqrt{-100}\).
Express it in terms of \(i\): \(\sqrt{-100} = \sqrt{100 \cdot -1}\).
Separate the square roots: \(\sqrt{100} \cdot \sqrt{-1}\).
Simplify the individual square roots: \(\sqrt{100} = 10\) and \(\sqrt{-1} = i\).
Combine the results: \(10 \cdot i = 10i\).
Thus, \(\sqrt{-100} = 10i\).
Example 3: Simplifying \(\sqrt{-18}\)
Identify the negative square root: \(\sqrt{-18}\).
Express it in terms of \(i\): \(\sqrt{-18} = \sqrt{18 \cdot -1}\).
Separate the square roots: \(\sqrt{18} \cdot \sqrt{-1}\).
Simplify the individual square roots. Since 18 is not a perfect square, break it down into its prime factors: \(18 = 9 \cdot 2\). So, \(\sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2}\).
Simplify the square root of -1: \(\sqrt{-1} = i\).
Combine the results: \(3\sqrt{2} \cdot i = 3i\sqrt{2}\).
Thus, \(\sqrt{-18} = 3i\sqrt{2}\).
Example 4: Simplifying \(\sqrt{-72}\)
Identify the negative square root: \(\sqrt{-72}\).
Express it in terms of \(i\): \(\sqrt{-72} = \sqrt{72 \cdot -1}\).
Separate the square roots: \(\sqrt{72} \cdot \sqrt{-1}\).
Simplify the individual square roots. Factor 72: \(72 = 36 \cdot 2\). So, \(\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}\).
Simplify the square root of -1: \(\sqrt{-1} = i\).
Combine the results: \(6\sqrt{2} \cdot i = 6i\sqrt{2}\).
Thus, \(\sqrt{-72} = 6i\sqrt{2}\).

Simplifying Negative Square Roots of Non-Perfect Squares
Simplifying negative square roots of non-perfect squares involves expressing the square root in its simplest form using the imaginary unit \(i\). Here's a detailed step-by-step process:
Identify the negative square root of a non-perfect square. For example, let's take \(\sqrt{-50}\).
Express the negative square root in terms of \(i\). Since \(\sqrt{-1} = i\), we can write \(\sqrt{-50}\) as \(\sqrt{50 \cdot -1}\).
Separate the expression into the product of two square roots: \(\sqrt{50} \cdot \sqrt{-1}\).
Simplify the square root of the non-perfect square. Factor the number inside the square root into its prime factors. For 50, we have \(50 = 25 \cdot 2\), so \(\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\).
Simplify the square root of -1: \(\sqrt{-1} = i\).
Combine the simplified results: \(5\sqrt{2} \cdot i = 5i\sqrt{2}\).
Thus, \(\sqrt{-50} = 5i\sqrt{2}\).
Let's look at more examples to solidify the process:
Example 1: Simplifying \(\sqrt{-12}\)
Identify the negative square root: \(\sqrt{-12}\).
Express it in terms of \(i\): \(\sqrt{-12} = \sqrt{12 \cdot -1}\).
Separate the square roots: \(\sqrt{12} \cdot \sqrt{-1}\).
Simplify the square root of 12. Factor 12: \(12 = 4 \cdot 3\). So, \(\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}\).
Simplify the square root of -1: \(\sqrt{-1} = i\).
Combine the results: \(2\sqrt{3} \cdot i = 2i\sqrt{3}\).
Thus, \(\sqrt{-12} = 2i\sqrt{3}\).
Example 2: Simplifying \(\sqrt{-45}\)
Identify the negative square root: \(\sqrt{-45}\).
Express it in terms of \(i\): \(\sqrt{-45} = \sqrt{45 \cdot -1}\).
Separate the square roots: \(\sqrt{45} \cdot \sqrt{-1}\).
Simplify the square root of 45. Factor 45: \(45 = 9 \cdot 5\). So, \(\sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5} = 3\sqrt{5}\).
Simplify the square root of -1: \(\sqrt{-1} = i\).
Combine the results: \(3\sqrt{5} \cdot i = 3i\sqrt{5}\).
Thus, \(\sqrt{-45} = 3i\sqrt{5}\).
Example 3: Simplifying \(\sqrt{-75}\)
Identify the negative square root: \(\sqrt{-75}\).
Express it in terms of \(i\): \(\sqrt{-75} = \sqrt{75 \cdot -1}\).
Separate the square roots: \(\sqrt{75} \cdot \sqrt{-1}\).
Simplify the square root of 75. Factor 75: \(75 = 25 \cdot 3\). So, \(\sqrt{75} = \sqrt{25 \cdot 3} = \sqrt{25} \cdot \sqrt{3} = 5\sqrt{3}\).
Simplify the square root of -1: \(\sqrt{-1} = i\).
Combine the results: \(5\sqrt{3} \cdot i = 5i\sqrt{3}\).
Thus, \(\sqrt{-75} = 5i\sqrt{3}\).
Handling Negative Square Roots in Fractions
Simplifying negative square roots in fractions involves a few additional steps compared to simplifying whole numbers. Here is a detailed, step-by-step guide:
Identify the fraction with a negative square root. For example, let's simplify \(\frac{\sqrt{-8}}{4}\).
Express the negative square root in terms of \(i\). Since \(\sqrt{-1} = i\), we can write \(\frac{\sqrt{-8}}{4}\) as \(\frac{\sqrt{8 \cdot -1}}{4}\).
Separate the square roots: \(\frac{\sqrt{8} \cdot \sqrt{-1}}{4}\).
Simplify the square root of the non-negative part. Factor 8: \(8 = 4 \cdot 2\), so \(\sqrt{8} = \sqrt{4 \cdot 2} = \sqrt{4} \cdot \sqrt{2} = 2\sqrt{2}\).
Simplify the square root of -1: \(\sqrt{-1} = i\).
Combine the results: \(\frac{2\sqrt{2} \cdot i}{4}\).
Simplify the fraction: \(\frac{2i\sqrt{2}}{4} = \frac{i\sqrt{2}}{2}\).
Thus, \(\frac{\sqrt{-8}}{4} = \frac{i\sqrt{2}}{2}\).
Let's look at more examples to solidify the process:
Example 1: Simplifying \(\frac{\sqrt{-18}}{6}\)
Identify the fraction: \(\frac{\sqrt{-18}}{6}\).
Express it in terms of \(i\): \(\frac{\sqrt{-18}}{6} = \frac{\sqrt{18 \cdot -1}}{6}\).
Separate the square roots: \(\frac{\sqrt{18} \cdot \sqrt{-1}}{6}\).
Simplify the square root of 18. Factor 18: \(18 = 9 \cdot 2\), so \(\sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2}\).
Simplify the square root of -1: \(\sqrt{-1} = i\).
Combine the results: \(\frac{3\sqrt{2} \cdot i}{6}\).
Simplify the fraction: \(\frac{3i\sqrt{2}}{6} = \frac{i\sqrt{2}}{2}\).
Thus, \(\frac{\sqrt{-18}}{6} = \frac{i\sqrt{2}}{2}\).
Example 2: Simplifying \(\frac{\sqrt{-27}}{3}\)
Identify the fraction: \(\frac{\sqrt{-27}}{3}\).
Express it in terms of \(i\): \(\frac{\sqrt{-27}}{3} = \frac{\sqrt{27 \cdot -1}}{3}\).
Separate the square roots: \(\frac{\sqrt{27} \cdot \sqrt{-1}}{3}\).
Simplify the square root of 27. Factor 27: \(27 = 9 \cdot 3\), so \(\sqrt{27} = \sqrt{9 \cdot 3} = \sqrt{9} \cdot \sqrt{3} = 3\sqrt{3}\).
Simplify the square root of -1: \(\sqrt{-1} = i\).
Combine the results: \(\frac{3\sqrt{3} \cdot i}{3}\).
Simplify the fraction: \(\frac{3i\sqrt{3}}{3} = i\sqrt{3}\).
Thus, \(\frac{\sqrt{-27}}{3} = i\sqrt{3}\).
Example 3: Simplifying \(\frac{\sqrt{-50}}{5}\)
Identify the fraction: \(\frac{\sqrt{-50}}{5}\).
Express it in terms of \(i\): \(\frac{\sqrt{-50}}{5} = \frac{\sqrt{50 \cdot -1}}{5}\).
Separate the square roots: \(\frac{\sqrt{50} \cdot \sqrt{-1}}{5}\).
Simplify the square root of 50. Factor 50: \(50 = 25 \cdot 2\), so \(\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\).
Simplify the square root of -1: \(\sqrt{-1} = i\).
Combine the results: \(\frac{5\sqrt{2} \cdot i}{5}\).
Simplify the fraction: \(\frac{5i\sqrt{2}}{5} = i\sqrt{2}\).
Thus, \(\frac{\sqrt{-50}}{5} = i\sqrt{2}\).
Practical Applications of Imaginary Numbers
Imaginary numbers, primarily represented by the unit i, find numerous applications in various fields. Here are some practical uses:
- Electrical Engineering: Imaginary numbers are crucial in analyzing AC circuits. They help represent and calculate impedance, enabling the design of efficient electrical systems.
- Signal Processing: In digital signal processing, imaginary numbers facilitate the manipulation of signals in the frequency domain using techniques like the Fourier transform.
- Control Systems: Imaginary numbers assist in modeling and controlling dynamic systems, helping to determine system stability through methods like root locus and Bode plots.
- Quantum Mechanics: The wave functions in quantum mechanics, which describe the probabilities of particles, often involve complex numbers, where the imaginary component plays a critical role in calculations.
- Fluid Dynamics: In fluid dynamics, potential flow solutions often employ complex analysis to solve two-dimensional flow problems.
These applications demonstrate the importance of imaginary numbers beyond theoretical mathematics, making them indispensable tools in engineering and physics.
Common Mistakes and How to Avoid Them
When simplifying negative square roots, it's essential to be aware of common pitfalls. Here are some frequent mistakes and strategies to avoid them:
- Forgetting to Identify Perfect Squares: Always check if there are any perfect square factors under the square root. This helps simplify the expression correctly. Tip: Factorize the number and look for pairs.
- Ignoring the Imaginary Unit: Remember that the square root of a negative number includes the imaginary unit \(i\). For instance, \(\sqrt{-9} = 3i\), not just \(3\).
- Incorrect Factorization: Ensure proper factorization to simplify completely. Double-check your factors to avoid errors.
- Misplacing the Negative Sign: The negative sign should remain outside the square root until the imaginary unit is applied. Correct: \(\sqrt{-16} = 4i\), not \(-4\).
- Overlooking Simplification in Fractions: When dealing with fractions, simplify both the numerator and the denominator separately before combining. This often reduces complexity.
By being mindful of these common mistakes, you can simplify negative square roots more effectively and avoid unnecessary errors.
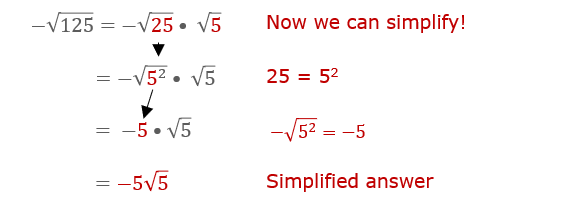
Advanced Techniques in Simplifying Complex Expressions
When dealing with complex expressions involving negative square roots, advanced techniques can greatly simplify the process. Here are some key strategies:
- Using Imaginary Units: Remember that the square root of a negative number can be expressed using the imaginary unit \(i\), where \(i = \sqrt{-1}\). For example, \(\sqrt{-9}\) simplifies to \(3i\).
- Factoring Radicands: Break down the radicand (the number inside the square root) into its prime factors. For example, \(\sqrt{-12}\) can be split into \(\sqrt{4 \cdot -3}\), which simplifies to \(2i\sqrt{3}\).
- Combining Like Terms: When simplifying expressions with multiple square roots, combine like terms where possible. For example, \(i\sqrt{2} + 3i\sqrt{2}\) simplifies to \(4i\sqrt{2}\).
- Applying Conjugates: In complex fractions, multiplying the numerator and denominator by the conjugate of the denominator can help eliminate imaginary numbers from the denominator, simplifying the expression.
These techniques not only simplify complex expressions but also make them easier to work with in further mathematical operations.
Conclusion and Summary
Simplifying negative square roots involves understanding the role of the imaginary unit \( i \), where \( i = \sqrt{-1} \). This allows us to express the square root of any negative number in terms of \( i \).
Throughout this guide, we've explored how to simplify these expressions by breaking them down into their components. For instance, \( \sqrt{-9} \) can be rewritten as \( 3i \), demonstrating the straightforward conversion from negative square roots to imaginary numbers.
Key points include:
- Recognizing the importance of the imaginary unit in complex numbers.
- Practicing simplification techniques to ensure accuracy in calculations.
- Applying these concepts to solve complex equations in algebra and beyond.
By mastering these skills, you enhance your ability to work with complex numbers and gain a deeper understanding of their applications in various mathematical and real-world contexts.
Video hướng dẫn cách đơn giản hóa căn bậc hai âm bằng cách sử dụng đơn vị ảo i, ví dụ với sqrt(-24).
Đại số 2 - Đơn giản hóa căn bậc hai âm sử dụng đơn vị ảo i, sqrt(-24)
READ MORE:
Hướng dẫn cách tìm căn bậc hai của số âm. Video này sẽ giúp bạn hiểu rõ hơn về khái niệm và cách thức tính toán căn bậc hai của các số âm.
Cách Tìm Căn Bậc Hai của Số Âm