Topic how to solve square roots equations: Unlock the mystery of square root equations with our comprehensive guide. Learn the essential steps, from isolating the square root to squaring both sides, simplifying, and verifying solutions. Master complex equations and discover advanced techniques to confidently solve any square root equation you encounter. Start solving square root equations today!
Table of Content
- How to Solve Square Root Equations
- Introduction
- Understanding Square Roots
- Basic Steps to Solve Square Root Equations
- Isolating the Square Root
- Squaring Both Sides of the Equation
- Simplifying the Resulting Equation
- Checking for Extraneous Solutions
- Examples of Solving Square Root Equations
- Solving Square Root Equations with Variables
- Complex Square Root Equations
- Factorizing Quadratic Equations
- Using the Quadratic Formula
- Rationalizing the Denominator
- Graphing Square Root Functions
- Common Mistakes to Avoid
- Practice Problems and Solutions
- Advanced Techniques
- Applications of Square Root Equations
- YOUTUBE:
How to Solve Square Root Equations
Solving square root equations involves isolating the square root on one side of the equation and then squaring both sides to eliminate the square root. Below are detailed steps and methods to solve square root equations:
Steps to Solve Square Root Equations
- Isolate the Square Root: Move all terms with the square root to one side of the equation and all other terms to the opposite side.
- Square Both Sides: Once the square root is isolated, square both sides of the equation to remove the square root.
- Simplify: Simplify the resulting equation. This may involve solving a linear or quadratic equation.
- Check for Extraneous Solutions: Substitute the solutions back into the original equation to verify they are valid.
Example
Consider the equation:
\[\sqrt{x + 5} = 3\]
- Isolate the square root: \(\sqrt{x + 5} = 3\)
- Square both sides: \((\sqrt{x + 5})^2 = 3^2\)
- Simplify: \(x + 5 = 9\)
- Solve for \(x\): \(x = 9 - 5 = 4\)
- Check the solution: \(\sqrt{4 + 5} = \sqrt{9} = 3\) (valid solution)
Solving Equations with Square Roots on Both Sides
When an equation has square roots on both sides, follow these steps:
- Isolate one of the square roots.
- Square both sides of the equation.
- Simplify and solve the resulting equation.
- Check all potential solutions for validity.
Example
Consider the equation:
\[\sqrt{2x + 3} = \sqrt{x + 9}\]
- Square both sides: \((\sqrt{2x + 3})^2 = (\sqrt{x + 9})^2\)
- Simplify: \(2x + 3 = x + 9\)
- Solve for \(x\): \(2x - x = 9 - 3\)
- \(x = 6\)
- Check the solution: \(\sqrt{2(6) + 3} = \sqrt{6 + 9} \Rightarrow \sqrt{15} = \sqrt{15}\) (valid solution)
Handling More Complex Equations
For more complex square root equations, additional algebraic techniques may be necessary:
- Factorizing the resulting quadratic equation.
- Using the quadratic formula: \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
- Rationalizing denominators if the square root is in a fraction.
Example
Solve the equation:
\[\sqrt{x} + \sqrt{x - 2} = 2\]
- Isolate one of the square roots: \(\sqrt{x} = 2 - \sqrt{x - 2}\)
- Square both sides: \((\sqrt{x})^2 = (2 - \sqrt{x - 2})^2\)
- Expand and simplify: \(x = 4 - 4\sqrt{x - 2} + (x - 2)\)
- Isolate the remaining square root: \(4\sqrt{x - 2} = 2\)
- Solve for \(x\): \(\sqrt{x - 2} = \frac{1}{2} \Rightarrow x - 2 = \frac{1}{4} \Rightarrow x = 2.25\)
- Check the solution: \(\sqrt{2.25} + \sqrt{0.25} = 1.5 + 0.5 = 2\) (valid solution)
Practice Problems
- Solve \(\sqrt{3x + 1} = 4\)
- Solve \(\sqrt{5x - 7} = 2\sqrt{x}\)
- Solve \(\sqrt{x + 6} + \sqrt{x - 4} = 5\)
By following these methods and practicing with various types of square root equations, you can master solving square root equations efficiently and accurately.

READ MORE:
Introduction
Square root equations are equations in which the variable is inside a square root. Solving these equations requires isolating the square root on one side and then squaring both sides to eliminate it. This guide provides a comprehensive approach to understanding and solving square root equations effectively.
In this section, we will cover:
- Understanding the basics of square roots
- Steps to solve simple and complex square root equations
- Methods to check for extraneous solutions
- Examples and practice problems
Let's begin by exploring the fundamental concepts of square roots and the importance of isolating the square root in an equation.
Understanding Square Roots
Square roots are mathematical operations that determine what number, when multiplied by itself, will equal the given number. For example, the square root of 16 is 4, because \(4 \times 4 = 16\). The square root is represented by the radical symbol \(\sqrt{}\).
Key points to understand about square roots include:
- Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\).
- Principal Square Root: The principal square root is the non-negative square root of a number. For any non-negative number \(x\), \(\sqrt{x} \geq 0\).
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are integers (e.g., \(\sqrt{16} = 4\)).
- Properties of Square Roots:
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
- Irrational Numbers: The square root of a non-perfect square is an irrational number, meaning it cannot be expressed as a simple fraction (e.g., \(\sqrt{2}\)).
- Negative Numbers: The square root of a negative number is not a real number, but an imaginary number, denoted as \(i\). For example, \(\sqrt{-1} = i\).
Understanding these fundamental concepts is crucial when solving square root equations. It helps in identifying the nature of solutions and applying the appropriate methods to simplify and solve the equations effectively.
Basic Steps to Solve Square Root Equations
Solving square root equations involves several important steps to isolate and eliminate the square root. Follow these steps to solve square root equations effectively:
- Isolate the Square Root:
Ensure that the square root term is on one side of the equation by itself. For example, if you have an equation like:
\(\sqrt{x+3} = 7\)
The square root is already isolated.
- Square Both Sides of the Equation:
To eliminate the square root, square both sides of the equation. This will remove the square root. For example:
\((\sqrt{x+3})^2 = 7^2\)
Which simplifies to:
\(x + 3 = 49\)
- Simplify the Resulting Equation:
After squaring both sides, you will have a new equation without the square root. Solve this equation as you would any other algebraic equation. For the example above:
\(x + 3 = 49\)
Subtract 3 from both sides:
\(x = 46\)
- Check for Extraneous Solutions:
Sometimes, squaring both sides of an equation can introduce extraneous solutions—solutions that do not satisfy the original equation. Always substitute your solutions back into the original equation to verify their validity. For the example above:
Substitute \(x = 46\) back into the original equation:
\(\sqrt{46 + 3} = 7\)
\(\sqrt{49} = 7\)
This is true, so \(x = 46\) is a valid solution.
Isolating the Square Root
When solving square root equations, the first step is to isolate the square root expression. This means getting the square root term by itself on one side of the equation. Here are the steps to isolate the square root:
- Identify the square root term: Look for the term under the square root symbol. For example, in the equation \(\sqrt{x+3} + 2 = 5\), the square root term is \(\sqrt{x+3}\).
- Move other terms to the opposite side: Use basic algebraic operations (addition, subtraction, multiplication, or division) to move other terms away from the square root term. Continuing with our example:
- Subtract 2 from both sides to isolate the square root term: \(\sqrt{x+3} + 2 - 2 = 5 - 2\)
- This simplifies to: \(\sqrt{x+3} = 3\)
Now that the square root term is isolated, the next step is to eliminate the square root by squaring both sides of the equation.

Squaring Both Sides of the Equation
Once you have isolated the square root on one side of the equation, the next step is to eliminate the square root by squaring both sides. Here is a detailed step-by-step process:
-
Start with the isolated square root equation:
\(\sqrt{a} = b\) -
Square both sides of the equation. Squaring both sides will eliminate the square root:
\((\sqrt{a})^2 = b^2\)This simplifies to:
a = b^2 -
Solve the resulting equation. After squaring both sides, you will have a polynomial equation that you can solve using algebraic methods:
Example:
Suppose you have the equation:
\(\sqrt{2x + 3} = 5\)Square both sides:
\((\sqrt{2x + 3})^2 = 5^2\)Simplify:
2x + 3 = 25Solve for \(x\):
2x = 22x = 11 -
Check for extraneous solutions. Squaring both sides can introduce extraneous solutions that do not satisfy the original equation. Substitute your solutions back into the original equation to verify:
For the example above, check \(x = 11\):
\(\sqrt{2(11) + 3} = 5\)\(\sqrt{25} = 5\)5 = 5\)Since the equation holds true, \(x = 11\) is a valid solution.
It's important to always check your solutions by substituting them back into the original equation to ensure they are not extraneous.
Simplifying the Resulting Equation
Once you have squared both sides of the equation, you will need to simplify the resulting equation. Here are the detailed steps to simplify:
- Expand any squared binomials: If you have squared a binomial, expand it using the formula \((a + b)^2 = a^2 + 2ab + b^2\).
- Combine like terms: Gather all similar terms on both sides of the equation. This often means combining constants and like variables.
- Move all terms to one side: To solve the resulting polynomial equation, move all terms to one side of the equation to set it to zero.
- Factor the polynomial: If possible, factor the polynomial to find the roots. Use factoring techniques such as factoring by grouping, the quadratic formula, or synthetic division.
- Solve for the variable: Set each factor equal to zero and solve for the variable to find potential solutions.
Here are a few examples to illustrate the simplification process:
Example 1
Simplify the equation \( (\sqrt{x} - 2)^2 = 9 \):
- Expand the binomial:
\[ (\sqrt{x} - 2)^2 = (\sqrt{x})^2 - 2 \cdot \sqrt{x} \cdot 2 + 2^2 \]
\[ (\sqrt{x} - 2)^2 = x - 4\sqrt{x} + 4 \]
- Set the equation to zero:
\[ x - 4\sqrt{x} + 4 = 9 \]
\[ x - 4\sqrt{x} + 4 - 9 = 0 \]
\[ x - 4\sqrt{x} - 5 = 0 \]
- Solve for \( x \):
Since this is a quadratic equation in terms of \( \sqrt{x} \), let \( y = \sqrt{x} \).
\[ y^2 - 4y - 5 = 0 \]
Factor the quadratic equation:
\[ (y - 5)(y + 1) = 0 \]
So, \( y = 5 \) or \( y = -1 \).
Since \( y = \sqrt{x} \), \( \sqrt{x} = 5 \) or \( \sqrt{x} = -1 \).
The solution \( \sqrt{x} = -1 \) is not valid since the square root of a number cannot be negative.
Therefore, \( \sqrt{x} = 5 \) which means \( x = 25 \).
Example 2
Simplify the equation \( (\sqrt{y - 3})^2 = 4 \):
- Square both sides:
\[ y - 3 = 16 \]
- Move terms to isolate \( y \):
\[ y - 3 + 3 = 16 + 3 \]
\[ y = 19 \]
Always verify your solutions by substituting them back into the original equation to check for extraneous solutions.
Checking for Extraneous Solutions
When solving square root equations, it's crucial to check for extraneous solutions, which are solutions that may appear valid but do not satisfy the original equation. Follow these steps to ensure your solutions are correct:
- After solving the equation, substitute each solution back into the original equation to verify its validity.
- Ensure that each substitution results in a true statement.
- Pay special attention to equations where the original problem might restrict the domain of the solutions, such as those involving square roots of variables or expressions under square roots.
- Be cautious of solutions that involve operations or transformations that could introduce non-permissible values into the equation.
By carefully checking for extraneous solutions, you can confidently determine the correct solutions to square root equations.
Examples of Solving Square Root Equations
Here are some detailed examples illustrating the process of solving square root equations:
- Solve \( \sqrt{x+3} = 5 \).
- Solve \( \sqrt{2y - 1} = 3 \).
- Solve \( \sqrt{4z} - 2 = 3 \).
Start by squaring both sides: \( x + 3 = 25 \).
Subtract 3 from both sides: \( x = 22 \).
Square both sides: \( 2y - 1 = 9 \).
Add 1 to both sides: \( 2y = 10 \).
Divide both sides by 2: \( y = 5 \).
Add 2 to both sides: \( \sqrt{4z} = 5 \).
Square both sides: \( 4z = 25 \).
Divide both sides by 4: \( z = 6.25 \).
These examples demonstrate the step-by-step process of solving various types of square root equations. Practice similar problems to master this technique.
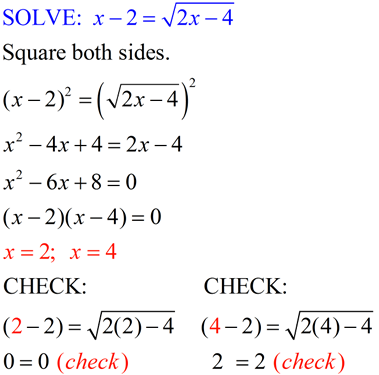
Solving Square Root Equations with Variables
When dealing with square root equations that involve variables, follow these steps to find the solution:
- Isolate the square root expression on one side of the equation.
- Square both sides of the equation to eliminate the square root.
- Solve the resulting equation for the variable.
- Check for extraneous solutions by substituting the obtained values back into the original equation.
- Ensure that the solutions satisfy any domain restrictions imposed by the problem.
By systematically following these steps, you can effectively solve square root equations where variables are involved.
Complex Square Root Equations
Complex square root equations involve scenarios where additional steps are needed to solve them. Follow these guidelines to tackle complex square root equations:
- Isolate the square root expression on one side of the equation.
- Square both sides to eliminate the square root.
- Continue solving the resulting equation, taking care to handle any remaining square roots or complex terms.
- Check for extraneous solutions by substituting the solutions back into the original equation.
- Ensure all solutions adhere to any domain restrictions specified by the problem.
By methodically applying these steps, you can effectively solve complex square root equations encountered in various mathematical contexts.
Factorizing Quadratic Equations
Factorizing quadratic equations with square roots involves these steps:
- Move all terms to one side of the equation to set it to zero.
- Identify and apply the appropriate factoring method, such as difference of squares or grouping.
- Factor out the quadratic expression to obtain two binomial factors.
- Set each binomial factor equal to zero and solve for the variable.
- Verify each solution by substituting it back into the original equation.
Mastering the skill of factorizing quadratic equations simplifies solving complex equations involving square roots.
Using the Quadratic Formula
The quadratic formula is a powerful tool to solve equations involving square roots. Follow these steps to utilize the quadratic formula:
- Identify the coefficients \( a \), \( b \), and \( c \) from the quadratic equation \( ax^2 + bx + c = 0 \).
- Substitute the values of \( a \), \( b \), and \( c \) into the quadratic formula: \( x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}} \).
- Calculate the values of \( x \) by evaluating both the positive and negative roots.
- Verify each solution by substituting it back into the original equation to ensure correctness.
By following these steps, you can confidently use the quadratic formula to solve equations containing square roots.

Rationalizing the Denominator
When faced with square roots in the denominator, rationalizing the denominator is necessary to simplify the expression. Follow these steps:
- Multiply both the numerator and the denominator by the conjugate of the denominator.
- Simplify the resulting expression to eliminate the square root from the denominator.
- Verify the simplified expression to ensure correctness.
By applying these steps, you can effectively rationalize the denominator in equations involving square roots.
Graphing Square Root Functions
Graphing square root functions involves understanding their basic properties and transformations. Follow these steps to graph a square root function:
- Identify the parent function \( y = \sqrt{x} \) and its domain and range.
- Apply transformations such as translations, reflections, and stretches/compressions if the function is modified.
- Plot key points using the transformed coordinates.
- Draw a smooth curve connecting the points to form the graph of the function.
- Label the axes and any significant points or intercepts on the graph.
By following these steps, you can accurately graph square root functions and visualize their behavior on the coordinate plane.
Common Mistakes to Avoid
When solving square root equations, be mindful of these common mistakes:
- Forgetting to check for extraneous solutions after squaring both sides.
- Misapplying operations when isolating square root terms.
- Ignoring domain restrictions that invalidate certain solutions.
- Incorrectly handling equations with square roots on both sides.
- Not verifying solutions by substituting them back into the original equation.
By being aware of these pitfalls, you can avoid errors and achieve accurate solutions in square root equations.
Practice Problems and Solutions
Below are several practice problems to help you master solving square root equations. Each problem is followed by a detailed solution using step-by-step explanations.
-
Problem 1: Solve \( \sqrt{x + 1} = 4 \)
- Given: \( \sqrt{x + 1} = 4 \)
- Square both sides: \( (\sqrt{x + 1})^2 = 4^2 \)
- Simplify: \( x + 1 = 16 \)
- Solve for \( x \): \( x = 16 - 1 \)
- Solution: \( x = 15 \)
- Check: \( \sqrt{15 + 1} = \sqrt{16} = 4 \) (Correct)
-
Problem 2: Solve \( \sqrt{3x + 1} = x - 3 \)
- Given: \( \sqrt{3x + 1} = x - 3 \)
- Square both sides: \( (\sqrt{3x + 1})^2 = (x - 3)^2 \)
- Simplify: \( 3x + 1 = x^2 - 6x + 9 \)
- Rearrange to form a quadratic equation: \( x^2 - 9x + 8 = 0 \)
- Factor the quadratic equation: \( (x - 8)(x - 1) = 0 \)
- Solutions: \( x = 8 \) or \( x = 1 \)
- Check solutions:
- For \( x = 8 \): \( \sqrt{3(8) + 1} = 8 - 3 \rightarrow \sqrt{25} = 5 \) (Correct)
- For \( x = 1 \): \( \sqrt{3(1) + 1} = 1 - 3 \rightarrow \sqrt{4} = -2 \) (Incorrect)
- Valid solution: \( x = 8 \)
-
Problem 3: Solve \( \sqrt{2x + 9} - 5 = 0 \)
- Given: \( \sqrt{2x + 9} - 5 = 0 \)
- Isolate the square root: \( \sqrt{2x + 9} = 5 \)
- Square both sides: \( (\sqrt{2x + 9})^2 = 5^2 \)
- Simplify: \( 2x + 9 = 25 \)
- Solve for \( x \): \( 2x = 16 \rightarrow x = 8 \)
- Check: \( \sqrt{2(8) + 9} - 5 = \sqrt{25} - 5 = 5 - 5 = 0 \) (Correct)
-
Problem 4: Solve \( \sqrt{2x - 5} - \sqrt{x - 1} = 1 \)
- Given: \( \sqrt{2x - 5} - \sqrt{x - 1} = 1 \)
- Isolate one square root: \( \sqrt{2x - 5} = 1 + \sqrt{x - 1} \)
- Square both sides: \( (\sqrt{2x - 5})^2 = (1 + \sqrt{x - 1})^2 \)
- Simplify: \( 2x - 5 = 1 + 2\sqrt{x - 1} + x - 1 \rightarrow 2x - 5 = 2\sqrt{x - 1} + x \)
- Isolate the remaining square root: \( x - 5 = 2\sqrt{x - 1} \)
- Square both sides again: \( (x - 5)^2 = (2\sqrt{x - 1})^2 \)
- Simplify: \( x^2 - 10x + 25 = 4(x - 1) \rightarrow x^2 - 10x + 25 = 4x - 4 \)
- Rearrange to form a quadratic equation: \( x^2 - 14x + 29 = 0 \)
- Solve using the quadratic formula: \( x = \frac{14 \pm \sqrt{196 - 116}}{2} = \frac{14 \pm 4\sqrt{5}}{2} \rightarrow x = 7 \pm 2\sqrt{5} \)
- Check solutions:
- For \( x = 7 + 2\sqrt{5} \): Calculate to verify if correct.
- For \( x = 7 - 2\sqrt{5} \): Calculate to verify if correct.
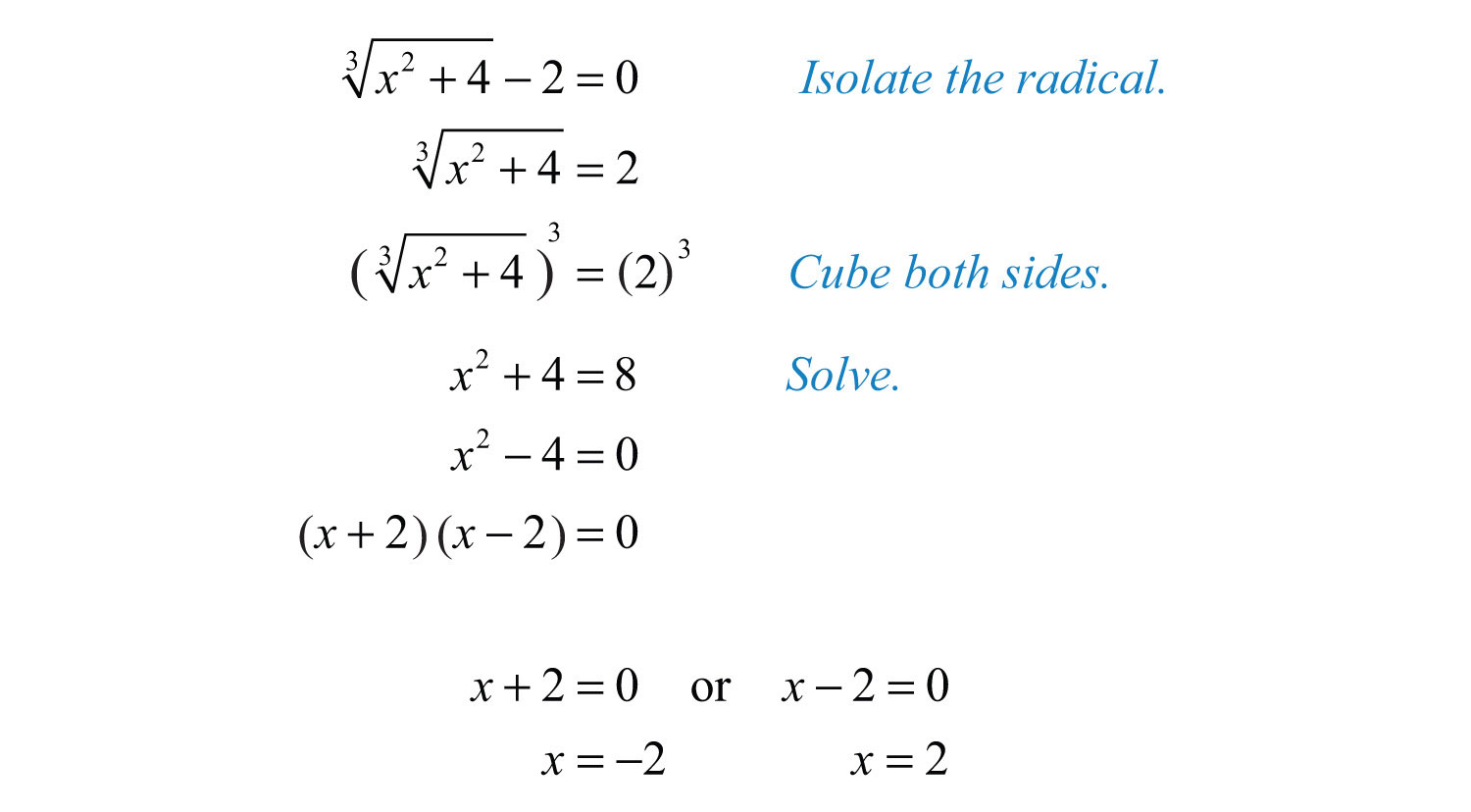
Advanced Techniques
Solving square root equations can sometimes require advanced techniques beyond basic isolation and squaring. Here, we explore some of these techniques to tackle more complex square root equations.
1. Completing the Square
Completing the square is a method used to solve quadratic equations that can be applied to equations involving square roots. This technique transforms a quadratic equation into a perfect square trinomial, making it easier to solve.
- Start with the equation in the form \(ax^2 + bx + c = 0\).
- Move the constant term to the other side: \(ax^2 + bx = -c\).
- Divide through by the coefficient of \(x^2\), if necessary, to make it 1: \(x^2 + \frac{b}{a}x = -\frac{c}{a}\).
- Add \(\left(\frac{b}{2a}\right)^2\) to both sides to complete the square: \(x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 = -\frac{c}{a} + \left(\frac{b}{2a}\right)^2\).
- Factor the left side: \(\left(x + \frac{b}{2a}\right)^2 = -\frac{c}{a} + \left(\frac{b}{2a}\right)^2\).
- Solve by taking the square root of both sides: \(x + \frac{b}{2a} = \pm \sqrt{-\frac{c}{a} + \left(\frac{b}{2a}\right)^2}\).
- Isolate \(x\): \(x = -\frac{b}{2a} \pm \sqrt{-\frac{c}{a} + \left(\frac{b}{2a}\right)^2}\).
2. Solving Equations with Multiple Radicals
When dealing with equations that have more than one square root term, isolate one of the radicals and then square both sides. This process may need to be repeated multiple times to eliminate all radicals.
- Isolate one of the radicals on one side of the equation.
- Square both sides to remove the isolated radical.
- Simplify the resulting equation and repeat the isolation and squaring steps if another radical is present.
- Continue this process until all radicals are eliminated, then solve the resulting polynomial equation.
- Check all potential solutions in the original equation to discard any extraneous solutions introduced by squaring.
3. Using Substitution
Substitution can simplify the process of solving complex square root equations by reducing them to a simpler form. This involves substituting a new variable for an expression involving the square root.
- Identify a part of the equation to substitute with a new variable. For example, let \(u = \sqrt{x + 3}\).
- Rewrite the equation in terms of the new variable. For example, if the equation is \(\sqrt{x + 3} + \sqrt{x - 2} = 5\), substitute \(u\) to get \(u + \sqrt{x - 2} = 5\).
- Solve the resulting equation for the new variable.
- Substitute back the original expression for the new variable and solve for the original variable.
4. Applying the Quadratic Formula
For equations that simplify to a quadratic form after isolating and squaring, the quadratic formula can be used to find the solutions.
- Rewrite the equation in standard quadratic form: \(ax^2 + bx + c = 0\).
- Apply the quadratic formula: \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\).
- Solve for \(x\) and simplify the solutions.
These advanced techniques expand the toolkit for solving square root equations, making it possible to tackle more complex problems with confidence.
Applications of Square Root Equations
Square root equations play a significant role in various fields. Here are some practical applications:
1. Finance
Square roots are used in finance to calculate stock market volatility. The volatility is the square root of the variance in the stock's return, helping investors assess the risk of investments.
2. Architecture
In architecture and engineering, square roots help determine the natural frequency of structures. This is essential for predicting how buildings and bridges react to loads such as wind and traffic.
3. Science
Scientists use square roots in various calculations, such as determining the velocity of objects, the amount of radiation absorbed by materials, and the intensity of sound waves. These calculations are crucial for technological development and scientific understanding.
4. Statistics
In statistics, square roots are used to compute the standard deviation, a measure of data spread. The standard deviation is the square root of the variance, which helps in data analysis and decision-making.
5. Geometry
Square roots are fundamental in geometry for calculating areas and perimeters of shapes, and in solving problems involving right triangles through the Pythagorean theorem.
6. Computer Science
In computer programming, square roots are used in encryption algorithms, image processing, and game physics, aiding in data security, visual effects, and realistic simulations.
7. Cryptography
Cryptography uses square roots in digital signatures, key exchange systems, and secure communication channels to authenticate and protect data transactions.
8. Navigation
Pilots and navigators use square roots to calculate distances and bearings between points on maps, essential for accurate course plotting.
9. Electrical Engineering
Square roots are used to calculate power, voltage, and current in electrical circuits, and in designing filters and signal-processing devices.
10. Photography
The f-number of a camera lens, which controls light entering the camera, is related to the square root of the aperture area, affecting the exposure of photographs.
11. Computer Graphics
In 2D and 3D graphics, square roots are used to calculate distances between points and lengths of vectors, important for rendering accurate images.
12. Telecommunication
In wireless communication, signal strength decreases with the square of the distance from the transmitter, following the inverse square law, crucial for designing communication systems.
13. Cooking
Scaling recipes involves using square roots to adjust ingredient quantities, ensuring balanced flavors in different batch sizes.
Practice Problems and Solutions
- Calculate the standard deviation of a data set where the variance is 25.
- Find the natural frequency of a structure if the square root of the stiffness divided by mass is 10.
- Determine the distance between two points (3, 4) and (0, 0) using the Pythagorean theorem.
These examples show how square root equations are integral to various real-world applications, enhancing our understanding and problem-solving abilities across multiple disciplines.
Học Cách Giải Phương Trình Căn Bậc Hai
READ MORE:
Hướng dẫn chi tiết cách giải các phương trình căn bậc hai, căn bậc ba, hai căn, phân số và lũy thừa phân số. Thích hợp cho người mới học và muốn nắm vững kiến thức cơ bản.
Giải Phương Trình Căn Bậc Hai, Căn Bậc Ba, Hai Căn, Phân Số, Lũy Thừa Phân Số