Topic how to solve square roots by hand: Discover the fascinating process of solving square roots by hand! This comprehensive guide breaks down the steps and methods, making it easy to understand and apply. Perfect for students, educators, or anyone curious about the math behind the magic, our step-by-step approach will help you master this essential skill.
Table of Content
- How to Solve Square Roots by Hand
- Introduction to Square Roots
- Understanding the Basics of Square Roots
- Methods to Solve Square Roots by Hand
- Step-by-Step Guide to Long Division Method
- Example Problems Using Long Division Method
- Estimating Square Roots by Guess-and-Check
- Prime Factorization Method
- Using the Babylonian Method
- Finding Square Roots of Non-Perfect Squares
- Examples and Practice Problems
- Comparing Different Methods
- Common Mistakes and How to Avoid Them
- Applications of Square Roots in Real Life
- Advanced Techniques and Tips
- Conclusion and Additional Resources
- YOUTUBE: Hướng dẫn cách tìm căn bậc hai bằng tay mà không cần máy tính. Video này giúp bạn hiểu rõ các bước chi tiết và dễ dàng áp dụng.
How to Solve Square Roots by Hand
Solving square roots by hand can be accomplished using several methods. Here are detailed steps for the most common techniques:
Method 1: Prime Factorization
- Find the prime factors of the number under the square root.
- Pair the prime factors.
- Take one number from each pair.
- Multiply these numbers together to get the square root.
Example:
Find the square root of 144:
- Prime factors of 144: \(144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3\)
- Pairs: \( (2 \times 2), (2 \times 2), (3 \times 3) \)
- Take one number from each pair: \( 2, 2, 3 \)
- Multiply these numbers: \( 2 \times 2 \times 3 = 12 \)
Therefore, \(\sqrt{144} = 12\).
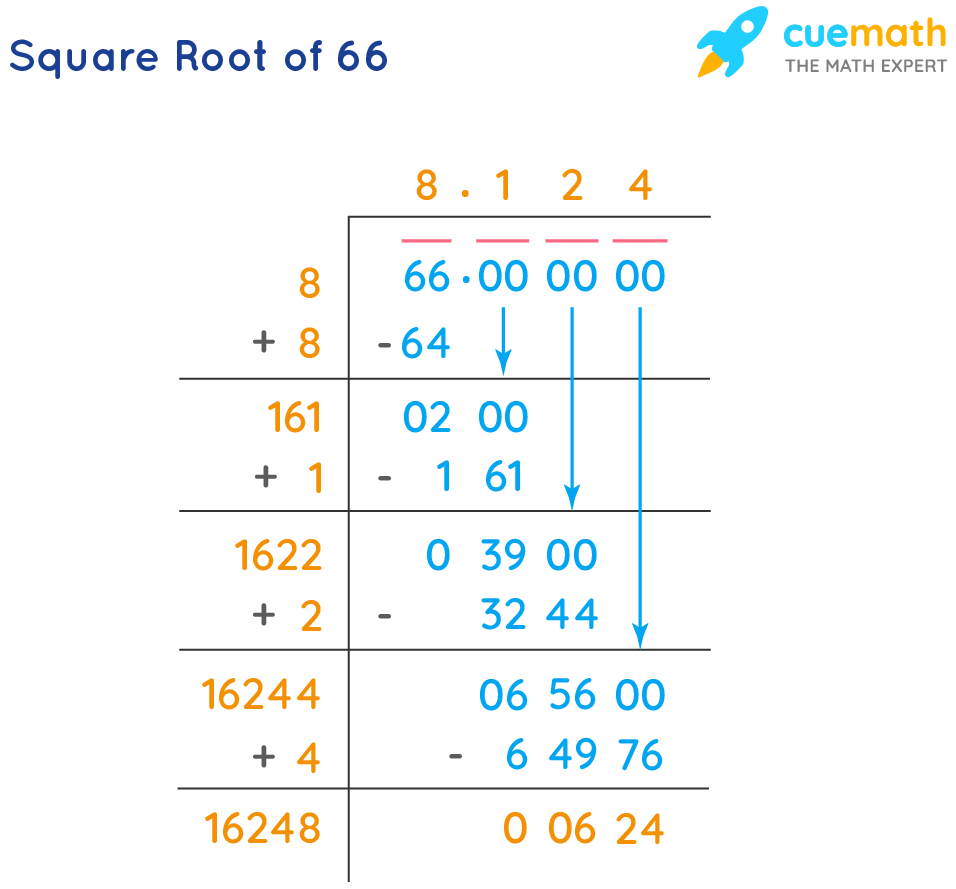
Method 2: Long Division Method
- Group the digits of the number in pairs, starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair.
- Subtract the square of this number from the first pair and bring down the next pair of digits.
- Double the number obtained in step 2 and write it as the new divisor with a blank digit place on the right.
- Find a digit to fill the blank that results in a product less than or equal to the current dividend.
- Repeat steps 3 to 5 until all pairs have been brought down.
Example:
Find the square root of 529:
- Pair the digits: 5 | 29
- Find the largest square less than 5: \(2^2 = 4\)
- Subtract and bring down the next pair: \(5 - 4 = 1\), bring down 29, making 129
- Double the current quotient (2): \(2 \times 2 = 4\), write as 40_
- Find the digit for blank: \(40x \leq 129\), \( x = 3 \), because \(403 \times 3 = 1209 \)
- Subtract: \(129 - 120 = 9\), bring down the next pair (if any)
- Continue the process until precision is achieved.
Therefore, \(\sqrt{529} = 23\).
Method 3: Estimation and Approximation
- Find the two perfect squares between which the number lies.
- Estimate the square root as a decimal value between these two square roots.
- Refine your estimate by averaging and adjusting.
Example:
Estimate the square root of 20:
- Perfect squares between which 20 lies: \(4^2 = 16\) and \(5^2 = 25\)
- Estimate: \(\sqrt{20} \approx 4.5\)
- Refine estimate: \(4.5^2 = 20.25\), so adjust downwards
- New estimate: \(\sqrt{20} \approx 4.47\)
Therefore, \(\sqrt{20} \approx 4.47\).
Conclusion
These methods provide a solid foundation for solving square roots by hand. Practice these techniques to improve your accuracy and speed.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics and appears frequently in various fields such as geometry, algebra, and calculus. A square root of a number n is a value that, when multiplied by itself, gives the number n. For example, the square root of 9 is 3 because 3 x 3 = 9.
Mathematically, the square root of n is denoted as \( \sqrt{n} \). Every positive number has two square roots: a positive root and a negative root. For instance, the square roots of 16 are 4 and -4, because both \( 4^2 \) and \( (-4)^2 \) equal 16. However, when we refer to "the square root," we usually mean the positive root, also known as the principal square root.
Understanding square roots involves familiarity with perfect squares. A perfect square is a number that is the square of an integer. Some common examples are:
- 1 ( \(1^2\) )
- 4 ( \(2^2\) )
- 9 ( \(3^2\) )
- 16 ( \(4^2\) )
- 25 ( \(5^2\) )
For non-perfect squares, such as 2 or 7, the square roots are irrational numbers, which cannot be expressed as simple fractions. Their decimal expansions are non-repeating and non-terminating. For example, \( \sqrt{2} \approx 1.414 \) and \( \sqrt{7} \approx 2.646 \).
Square roots are closely related to squaring. The operation of squaring a number and finding its square root are inverses of each other. If \( x^2 = n \), then \( x = \sqrt{n} \). This relationship is crucial in solving various algebraic equations.
To better understand square roots, consider the following table showing numbers and their square roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
In the following sections, we will explore various methods to solve square roots by hand, including techniques for perfect and non-perfect squares.
Understanding the Basics of Square Roots
A square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). In other words, it is a number that, when multiplied by itself, gives the original number. The square root is denoted by the radical symbol \( \sqrt{} \).
For example, the square root of 9 is 3 because \( 3 \times 3 = 9 \). Similarly, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \). Every positive number has two square roots: a positive and a negative one. Thus, \( \sqrt{9} = \pm 3 \).
In mathematical notation, the square root of \( x \) is written as \( \sqrt{x} \). For positive numbers, the principal square root is usually the positive one. However, both roots are valid: \( \sqrt{25} = \pm 5 \).
Key Properties of Square Roots
- Square of a Square Root: The square of a square root of a number gives the original number. For example, \( (\sqrt{5})^2 = 5 \).
- Product Property: The square root of a product is equal to the product of the square roots of the factors. Mathematically, \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Perfect Squares
Perfect squares are numbers that have integer square roots. Examples include 1, 4, 9, 16, 25, 36, etc. For these numbers, their square roots are whole numbers. For instance:
- \( \sqrt{1} = 1 \)
- \( \sqrt{4} = 2 \)
- \( \sqrt{9} = 3 \)
Non-Perfect Squares
Numbers that do not have integer square roots are called non-perfect squares. Their square roots are irrational numbers, which cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions. Examples include:
- \( \sqrt{2} \approx 1.414 \)
- \( \sqrt{3} \approx 1.732 \)
- \( \sqrt{5} \approx 2.236 \)
Square Roots of Negative Numbers
Square roots of negative numbers involve imaginary numbers. The imaginary unit \( i \) is defined as \( \sqrt{-1} \). Therefore, the square root of any negative number can be expressed in terms of \( i \). For example:
- \( \sqrt{-4} = 2i \)
- \{ \sqrt{-9} = 3i \)
Square Roots in Geometry
In geometry, the square root often appears when dealing with areas. For example, the side length of a square can be found if the area is known. If a square has an area of \( A \), then each side is \( \sqrt{A} \).
Understanding these basic concepts of square roots is essential as they form the foundation for more advanced topics in mathematics.
Methods to Solve Square Roots by Hand
There are several methods to solve square roots by hand, each with its own steps and level of complexity. Here, we will explore some of the most commonly used methods: the Long Division Method, the Prime Factorization Method, and the Babylonian Method.
1. Long Division Method
The Long Division Method is a step-by-step process similar to traditional long division. Here's how to use it:
- Separate the digits into pairs: Start from the decimal point and move left and right. For example, for the number 2025, write it as 20 25.
- Find the largest square: Determine the largest number whose square is less than or equal to the first pair. For 20, the largest square is 16 (4²), so 4 is the first digit of the square root.
- Subtract and bring down: Subtract the square of 4 from 20 to get 4. Bring down the next pair (25), making the number 425.
- Double the current root: Double the current digit (4) to get 8. Write this as the first part of the new divisor.
- Find the next digit: Find a digit (d) such that 8d × d ≤ 425. Here, 85 × 5 = 425, so d = 5.
- Repeat if necessary: If there are more digits, continue the process. Otherwise, the square root of 2025 is 45.
2. Prime Factorization Method
The Prime Factorization Method involves breaking down a number into its prime factors and pairing them to find the square root. Follow these steps:
- Factorize the number: Express the number as a product of prime factors. For example, 144 = 2 × 2 × 2 × 2 × 3 × 3.
- Pair the factors: Pair the prime factors. For 144, we get (2 × 2), (2 × 2), and (3 × 3).
- Take one from each pair: Take one factor from each pair. Here, it's 2, 2, and 3.
- Multiply the factors: Multiply these factors together to get the square root. For 144, the square root is 2 × 2 × 3 = 12.
3. Babylonian Method (Heron's Method)
The Babylonian Method is an iterative approach to approximate the square root. Here's how to do it:
- Initial guess: Start with an initial guess (x₀). For √10, let's guess 3.
- Iterate: Use the formula x₁ = (x₀ + (n / x₀)) / 2. For the first iteration with n = 10 and x₀ = 3, we get x₁ = (3 + 10/3) / 2 = 3.1667.
- Repeat: Use x₁ as the new guess and repeat the process until the result is accurate enough. Each iteration brings the value closer to the true square root.
These methods provide a foundation for solving square roots by hand, allowing for practice and a deeper understanding of the concept.
Step-by-Step Guide to Long Division Method
The long division method is a systematic way to find the square root of a number by hand. Here is a step-by-step guide to help you through the process:
-
Separate the Digits:
Start by grouping the digits of the number in pairs from right to left. For example, to find the square root of 104976, we group it as 10,49,76.
-
Find the Largest Integer:
Identify the largest integer whose square is less than or equal to the first group. For 10, it is 3 because \(3^2 = 9\).
-
Subtract and Bring Down the Next Pair:
Subtract the square from the first group and bring down the next pair. In this case, 10 - 9 = 1, bringing down 49 to make 149.
-
Double the Quotient and Find the Next Digit:
Double the current quotient (3), and find a digit to form a number that, when multiplied by itself, is less than or equal to 149. The new number is 6 because 6 × 6 = 36.
-
Repeat the Process:
Repeat steps 3 and 4 with the new pairs of digits and the new quotient until you reach the desired level of accuracy. For 104976, the next pair is 76, making the current dividend 76, and so on.
-
Continue Until Completion:
Keep repeating the steps until you have worked through all digit pairs. The final quotient will be the square root. For 104976, the process will yield 324 as the square root.
By following these steps, you can manually find the square root of any number using the long division method. Practice with different numbers to get comfortable with the process.

Example Problems Using Long Division Method
Let's go through some example problems to understand how the long division method can be used to find square roots.
Example 1: Finding the Square Root of 225
To find the square root of 225 using the long division method, follow these steps:
- Pair the Digits: 225 is already a three-digit number. Pair the digits from right to left: (2)(25).
- Find the Largest Square: Find the largest number whose square is less than or equal to the first pair (2). Here, 1 is the largest number because \(1^2 = 1\).
- Subtract: Subtract 1 from 2: \(2 - 1 = 1\).
- Bring Down the Next Pair: Bring down the next pair (25) to the right of the remainder to get 125.
- Double the Quotient: The current quotient is 1. Double it to get 2.
- Find the Next Digit: Find a digit X such that \(2X \times X \leq 125\). Here, 25 works because \(25 \times 5 = 125\).
- Calculate the Remainder: Subtract 125 from 125: \(125 - 125 = 0\). The remainder is 0.
Thus, the square root of 225 is 15.
Example 2: Finding the Square Root of 83
To find the square root of 83 using the long division method, follow these steps:
- Pair the Digits: Since 83 is a two-digit number, pair the digits: (83).
- Find the Largest Square: Find the largest number whose square is less than or equal to the first pair (8). Here, 2 is the largest number because \(2^2 = 4\).
- Subtract: Subtract 4 from 8: \(8 - 4 = 4\).
- Bring Down the Next Pair: Bring down the next digit (3) to the right of the remainder to get 43.
- Double the Quotient: The current quotient is 2. Double it to get 4.
- Find the Next Digit: Find a digit X such that \(4X \times X \leq 43\). Here, 42 works because \(42 \times 1 = 42\).
- Calculate the Remainder: Subtract 42 from 43: \(43 - 42 = 1\). The remainder is 1.
Since we still have a remainder, we can add decimal places and continue the process to get a more precise value. The approximate square root of 83 is 9.11.
Example 3: Finding the Square Root of 200
To find the square root of 200 using the long division method, follow these steps:
- Pair the Digits: 200 is a three-digit number. Pair the digits from right to left: (2)(00).
- Find the Largest Square: Find the largest number whose square is less than or equal to the first pair (2). Here, 1 is the largest number because \(1^2 = 1\).
- Subtract: Subtract 1 from 2: \(2 - 1 = 1\).
- Bring Down the Next Pair: Bring down the next pair (00) to the right of the remainder to get 100.
- Double the Quotient: The current quotient is 1. Double it to get 2.
- Find the Next Digit: Find a digit X such that \(2X \times X \leq 100\). Here, 42 works because \(20 \times 5 = 100\).
- Calculate the Remainder: Subtract 100 from 100: \(100 - 100 = 0\). The remainder is 0.
Thus, the square root of 200 is approximately 14.14.
Estimating Square Roots by Guess-and-Check
Estimating square roots by the guess-and-check method involves making an initial guess, checking it by squaring the guess, and then refining the guess based on how close it is to the target number. Here’s a step-by-step guide:
-
Start with an initial guess. For example, to estimate the square root of 20, you might start with a guess of 4.
-
Square your guess. In this case, \(4^2 = 16\).
-
Compare the squared result to the target number. If the square is less than the target, increase your guess; if it's more, decrease your guess. Since \(16 < 20\), increase the guess.
-
Make a new guess. Let's try 4.5.
-
Square the new guess: \(4.5^2 = 20.25\).
-
Compare again. Since \(20.25 > 20\), decrease the guess slightly. Try 4.4 next.
-
Square this new guess: \(4.4^2 = 19.36\).
-
Continue this process. Next, try 4.45: \(4.45^2 = 19.8025\), then 4.46: \(4.46^2 = 19.8916\), and finally 4.47: \(4.47^2 = 19.9809\).
-
Refine the guess until the squared value is as close as possible to the target number. In this case, \( \sqrt{20} \approx 4.47 \).
Through repeated guessing and checking, you can get very close to the actual square root. This method is effective for finding approximate values when an exact calculation is not required.
Here are a few more examples to practice:
- Estimate \( \sqrt{7} \): Start with 2, then 2.5, and refine to approximately 2.646.
- Estimate \( \sqrt{50} \): Start with 7, then 7.1, and refine to approximately 7.071.
- Estimate \( \sqrt{100} \): Since 100 is a perfect square, the exact answer is 10.
Prime Factorization Method
The prime factorization method involves breaking down a number into its prime factors and then pairing these factors to simplify the extraction of the square root. Here's a detailed step-by-step guide on how to use this method:
-
Factorize the Number into Prime Factors:
Start by dividing the number by the smallest prime number (usually 2) that can exactly divide it without leaving a remainder. Continue this process with the quotient until you reach a prime number.
Example: To factorize 72:
- 72 ÷ 2 = 36
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
Prime factors of 72 are: \(2^3 \times 3^2\)
-
Organize the Prime Factors into Pairs:
Arrange the prime factors in a visible format and pair identical factors. If a factor does not have a pair, it remains single.
Example: From the prime factors \(2^3 \times 3^2\):
- Pairs: (2,2),(2),(3,3)
-
Multiply One Element from Each Pair:
For each pair of identical primes, select one prime from the pair and multiply them. If a prime remains unpaired, it stays under the square root.
Example: Pairs from \(2^3 \times 3^2\):
- Paired result is \(2 \times 3 = 6\)
- Unpaired prime is 2
The square root of 72 is \(6\sqrt{2}\).
-
Calculate the Square Root:
Multiply the results of the previous step together, and multiply this product by the square root of any leftover unpaired primes to find the square root of the original number.
Solved Examples
Here are some examples to illustrate the prime factorization method:
-
Square Root of 144:
- Prime factorization: \(144 = 2^4 \times 3^2\)
- Pairs: (2,2),(2,2),(3,3)
- Multiply one from each pair: \(2 \times 2 \times 3 = 12\)
- \(\sqrt{144} = 12\)
-
Square Root of 200:
- Prime factorization: \(200 = 2^3 \times 5^2\)
- Pairs: (2,2),(5,5)
- Unpaired: 2
- Multiply one from each pair: \(2 \times 5 = 10\)
- \(\sqrt{200} = 10\sqrt{2}\)
Using the Babylonian Method
The Babylonian method, also known as Heron's method, is an ancient and effective technique for approximating square roots. It is a specific case of the Newton-Raphson method and is known for its simplicity and quick convergence. Below is a step-by-step guide to using the Babylonian method:
- Start with an initial guess \( x_0 \) for the square root of the number \( S \) you want to find. A good starting point is \( x_0 = \frac{S}{2} \).
- Use the recursive formula to improve your guess: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \]
- Repeat the process until the difference between \( x_n \) and \( x_{n+1} \) is less than a desired tolerance level (e.g., \( 0.001 \) or \( 0.0001 \)).
Here is an example to illustrate the process:
- Find the square root of \( S = 25 \).
- Initial guess: \( x_0 = \frac{25}{2} = 12.5 \).
- First iteration: \[ x_1 = \frac{1}{2} \left( 12.5 + \frac{25}{12.5} \right) = \frac{1}{2} (12.5 + 2) = 7.25 \]
- Second iteration: \[ x_2 = \frac{1}{2} \left( 7.25 + \frac{25}{7.25} \right) = \frac{1}{2} (7.25 + 3.448) \approx 5.35 \]
- Third iteration: \[ x_3 = \frac{1}{2} \left( 5.35 + \frac{25}{5.35} \right) = \frac{1}{2} (5.35 + 4.673) \approx 5.01 \]
- Fourth iteration: \[ x_4 = \frac{1}{2} \left( 5.01 + \frac{25}{5.01} \right) = \frac{1}{2} (5.01 + 4.990) \approx 5.00 \]
After four iterations, the approximation \( x_4 \approx 5.00 \) is very close to the actual square root of 25.
The Babylonian method can be used for any positive number and converges quickly, often requiring only a few iterations to reach a high degree of accuracy.

Finding Square Roots of Non-Perfect Squares
Finding the square root of non-perfect squares can be challenging, but several methods can help you estimate or calculate the value accurately. Here are a few techniques you can use:
Method 1: Long Division Method
This method involves a step-by-step process similar to long division. Here's how you can do it:
- Separate the number into pairs of digits, starting from the decimal point. For example, to find the square root of 452, you would write it as 4 | 52.
- Find the largest number whose square is less than or equal to the first pair. Write this number above the pair. Subtract its square from the first pair and bring down the next pair.
- Double the current quotient and write it as a potential divisor. Find a digit to complete the divisor so that the product is as close as possible to the current number without exceeding it. Write this digit next to the quotient and repeat the process.
For example, to find √452:
| Step | Action | Result |
| 1 | Pair digits: 4 | 52 | |
| 2 | Largest square ≤ 4 is 2² = 4 | 2 |
| 3 | Double quotient: 2 × 2 = 4 | |
| 4 | Find next digit: 42 * 2 = 84 | 6 |
Method 2: Guess-and-Check Method
This method involves guessing a number and then refining the guess:
- Start with an initial guess. For example, to find the square root of 12, guess 3.
- Square the guess and compare it with the original number. Adjust the guess accordingly.
- Continue refining the guess until you reach the desired accuracy.
For example, to find √12:
- Guess: 3 → 3² = 9 (too low)
- Next guess: 3.5 → 3.5² = 12.25 (too high)
- Next guess: 3.4 → 3.4² = 11.56 (too low)
- Refine: 3.45 → 3.45² = 11.9025 (too low)
Method 3: Prime Factorization Method
For this method, you decompose the number into its prime factors and then pair the factors:
- Find the prime factors of the number.
- Pair the factors and take the square root of each pair.
- Multiply the results to get the final square root.
For example, to find √45:
- Prime factors: 45 = 3 × 3 × 5
- Pair the factors: (3 × 3) and 5
- Square root of each pair: √(3 × 3) = 3, √5
- Result: 3√5
Method 4: Babylonian (or Heron's) Method
This ancient method involves an iterative process:
- Start with an initial guess (x0).
- Apply the formula: xn+1 = (xn + N / xn) / 2
- Repeat until the result converges to a stable value.
For example, to find √16:
- Initial guess: 4
- Apply formula: (4 + 16 / 4) / 2 = 4.5
- Next iteration: (4.5 + 16 / 4.5) / 2 ≈ 4.1
- Continue until convergence: ≈ 4.00003
By using these methods, you can effectively find the square roots of non-perfect squares without relying on a calculator.
Examples and Practice Problems
Below are several examples and practice problems to help you master solving square roots by hand. Each example includes a detailed solution to guide you through the process. Try solving these problems on your own before checking the answers.
Example 1: Finding the Square Root of 25
To find the square root of 25:
- Identify a number that, when multiplied by itself, equals 25.
- Since \(5 \times 5 = 25\), the square root of 25 is 5.
\(\sqrt{25} = 5\)
Example 2: Finding the Square Root of 121
To find the square root of 121:
- Identify a number that, when multiplied by itself, equals 121.
- Since \(11 \times 11 = 121\), the square root of 121 is 11.
\(\sqrt{121} = 11\)
Example 3: Simplifying the Square Root of 32
To simplify the square root of 32:
- Rewrite \(32\) as \(16 \times 2\).
- Take the square root of each factor: \(\sqrt{16} \times \sqrt{2}\).
- Since \(\sqrt{16} = 4\), we have \(4 \sqrt{2}\).
\(\sqrt{32} = 4\sqrt{2}\)
Example 4: Simplifying the Square Root of 50
To simplify the square root of 50:
- Rewrite \(50\) as \(25 \times 2\).
- Take the square root of each factor: \(\sqrt{25} \times \sqrt{2}\).
- Since \(\sqrt{25} = 5\), we have \(5 \sqrt{2}\).
\(\sqrt{50} = 5\sqrt{2}\)
Example 5: Simplifying the Square Root of 132
To simplify the square root of 132:
- Rewrite \(132\) as \(4 \times 33\).
- Take the square root of each factor: \(\sqrt{4} \times \sqrt{33}\).
- Since \(\sqrt{4} = 2\), we have \(2 \sqrt{33}\).
\(\sqrt{132} = 2\sqrt{33}\)
Practice Problems
Try solving these practice problems to test your understanding:
- Find \(\sqrt{49}\).
- Find \(\sqrt{144}\).
- Simplify \(\sqrt{75}\).
- Simplify \(\sqrt{180}\).
Check your answers:
- \(\sqrt{49} = 7\)
- \(\sqrt{144} = 12\)
- \(\sqrt{75} = 5\sqrt{3}\)
- \(\sqrt{180} = 6\sqrt{5}\)
Comparing Different Methods
There are several methods to solve square roots by hand, each with its advantages and specific applications. Here, we will compare the three most common methods: the Long Division Method, the Prime Factorization Method, and the Babylonian Method (also known as Newton's Method).
1. Long Division Method
The Long Division Method is a traditional technique that provides an exact decimal value for the square root. It's particularly useful for finding the square roots of non-perfect squares with high precision.
- Pair the digits of the number from right to left.
- Find the largest number whose square is less than or equal to the first pair or single digit.
- Subtract the square of this number from the first pair and bring down the next pair of digits.
- Double the number obtained in the quotient and determine the next digit of the quotient by trial, ensuring the new number formed after placing the digit and multiplying is less than or equal to the current dividend.
- Repeat the process until all pairs are used up.
2. Prime Factorization Method
The Prime Factorization Method involves breaking down the number into its prime factors and then simplifying the square root. This method is straightforward for numbers with small prime factors.
- Factorize the number into its prime components.
- Group the prime factors into pairs of the same numbers.
- Take one number from each pair out of the square root.
- Multiply the numbers taken out to get the square root.
For example, to find the square root of 1764:
- Prime factors of 1764 are \( 2 \times 2 \times 3 \times 3 \times 7 \times 7 \)
- Grouping the factors: \( (2 \times 2) \times (3 \times 3) \times (7 \times 7) \)
- Taking one from each pair: \( 2 \times 3 \times 7 = 42 \)
- Thus, \( \sqrt{1764} = 42 \)
3. Babylonian Method (Newton's Method)
The Babylonian Method is an iterative approach that quickly converges to the square root. It is particularly efficient for large numbers and provides high accuracy with few iterations.
- Make an initial guess \( g \) for the square root.
- Compute the average of \( g \) and \( \frac{x}{g} \) where \( x \) is the number whose square root is being calculated.
- Use the result as the new guess and repeat the process until the desired accuracy is reached.
For instance, to find \( \sqrt{30} \):
- Initial guess: \( g = 5 \)
- First iteration: \( g = \frac{5 + \frac{30}{5}}{2} = 5.5 \)
- Second iteration: \( g = \frac{5.5 + \frac{30}{5.5}}{2} \approx 5.477 \)
Comparison
| Method | Precision | Complexity | Best Use Case |
|---|---|---|---|
| Long Division | High | Moderate | Exact decimal values |
| Prime Factorization | Moderate | Simple | Small numbers with simple prime factors |
| Babylonian Method | High | Low | Large numbers and iterative calculations |
Each method has its own strengths and is suited to different types of problems. Understanding these methods allows for flexibility in choosing the most appropriate technique for any given square root calculation.
Common Mistakes and How to Avoid Them
When solving square roots by hand, it's easy to make mistakes. Here are some common errors and tips on how to avoid them:
-
Mistake: Incorrectly simplifying square roots.
Example: \(\sqrt{0.09} = 0.3\)
Correction: \(\sqrt{0.09} = \sqrt{\frac{9}{100}} = \frac{\sqrt{9}}{\sqrt{100}} = \frac{3}{10} = 0.3\)
-
Mistake: Adding or subtracting square roots directly.
Example: \(3\sqrt{3} + 3 = 6\sqrt{3}\)
Correction: \(3\sqrt{3} + 3 = 3(\sqrt{3} + 1)\)
-
Mistake: Assuming \(\sqrt{x+y} = \sqrt{x} + \sqrt{y}\).
Example: \(\sqrt{9+16} \neq \sqrt{9} + \sqrt{16}\)
Correction: \(\sqrt{9+16} = \sqrt{25} = 5 \neq 3 + 4\)
-
Mistake: Incorrectly handling negative square roots.
Example: When solving \(x^2 = 9\), only finding \(x = 3\).
Correction: Remember that \(x = \pm 3\) since both \(3^2\) and \((-3)^2\) equal 9.
-
Mistake: Squaring binomials incorrectly.
Example: \((4a)^2 = 4a^2\)
Correction: \((4a)^2 = 4a \cdot 4a = 16a^2\)
-
Mistake: Incorrectly squaring decimals.
Example: \(0.2^2 = 0.4\)
Correction: \(0.2^2 = 0.2 \cdot 0.2 = 0.04\)
By being aware of these common mistakes and practicing regularly, you can improve your accuracy in solving square roots by hand.

Applications of Square Roots in Real Life
Square roots are not just abstract mathematical concepts; they have practical applications in various real-life scenarios. Here are some of the ways square roots are used:
-
Geometry and Construction: Square roots are essential in determining the length of the sides of a square when the area is known. For example, if the area of a square patio is 200 square feet, the length of each side can be calculated as:
\[\sqrt{200} \approx 14.14 \text{ feet}\]
-
Distance Between Points: In both two-dimensional and three-dimensional spaces, square roots are used to calculate the distance between two points. For instance, the distance \(D\) between points \((x_1, y_1)\) and \((x_2, y_2)\) in a plane is given by:
\[D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]
-
Physics and Gravity: Square roots help in calculating the time it takes for an object to fall to the ground when dropped from a certain height. The time \(t\) in seconds for an object to fall from a height \(h\) feet is:
\[t = \frac{\sqrt{h}}{4}\]
For example, if an object is dropped from a height of 64 feet:
\[t = \frac{\sqrt{64}}{4} = 2 \text{ seconds}\]
-
Accident Investigations: Police use square roots to determine the speed of a car based on the length of skid marks left on the road. If the length of the skid marks is \(d\) feet, the speed \(s\) of the car in miles per hour can be estimated by:
\[s = \sqrt{24d}\]
For example, if skid marks are 190 feet long:
\[s = \sqrt{24 \times 190} \approx 67.5 \text{ mph}\]
-
Quadratic Equations: Solving quadratic equations often involves finding the square root of a number. The quadratic formula for solving \(ax^2 + bx + c = 0\) is:
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
Here, the square root term \(\sqrt{b^2 - 4ac}\) is crucial in finding the roots of the equation.
These examples illustrate the importance and utility of square roots in various fields, from everyday tasks to specialized scientific applications.
Advanced Techniques and Tips
When solving square roots by hand, there are several advanced techniques and tips that can help you achieve more accurate results more efficiently. Here are some key methods:
1. Using Averaging Method
This method involves iteratively averaging numbers to narrow down the square root:
- Estimate a rough boundary. For example, to find \(\sqrt{20}\), note that \(4^2 = 16\) and \(5^2 = 25\), so \(\sqrt{20}\) is between 4 and 5.
- Take the average of 4 and 5: \(\frac{4 + 5}{2} = 4.5\).
- Square 4.5 to get 20.25, which is slightly above 20.
- Adjust the boundary to 4 and 4.5 and repeat the process: \(\frac{4 + 4.5}{2} = 4.25\).
- Square 4.25 to get 18.0625, which is below 20. Adjust the boundary again to 4.25 and 4.5 and continue.
Continue this process until the boundary is sufficiently narrow for your desired precision.
2. Newton-Raphson Method
The Newton-Raphson method is a powerful technique for finding successively better approximations to the roots of a real-valued function:
- Start with an initial guess, \(x_0\), close to \(\sqrt{a}\).
- Apply the iteration formula: \(x_{n+1} = \frac{1}{2} \left( x_n + \frac{a}{x_n} \right)\).
- Repeat the process until \(x_n\) converges to a stable value.
For example, to find \(\sqrt{10}\), start with \(x_0 = 3\):
- \(x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667\)
- \(x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) \approx 3.1623\)
- Continue iterating until \(x_n\) stabilizes.
3. Prime Factorization Method
Prime factorization helps in simplifying square roots of non-perfect squares:
- Express the number as a product of its prime factors. For example, 72 = 23 \(\times\) 32.
- Group the prime factors into pairs: 72 = (2 \(\times\) 2) \(\times\) 2 \(\times\) (3 \(\times\) 3).
- Take one number from each pair outside the square root: \(\sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
4. Using Approximations and Patterns
Recognize patterns and use approximations for faster calculations:
- Memorize squares of common numbers (e.g., 1 to 25).
- Use the fact that \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\) for easier numbers.
- Employ linear approximations for numbers close to known squares.
By combining these advanced techniques, you can efficiently and accurately solve square roots by hand, even for more complex numbers.
Conclusion and Additional Resources
Solving square roots by hand is a valuable skill that enhances your understanding of mathematics and improves problem-solving abilities. Throughout this guide, we have explored various methods, including the long division method, guess-and-check, prime factorization, and the Babylonian method. Each technique offers a unique approach to finding square roots, and practicing these methods will build your confidence in tackling mathematical problems.
Remember, the key to mastering these methods is practice and patience. As you continue to work on different examples, you'll find that your ability to solve square roots by hand will improve significantly. Additionally, understanding these techniques provides a strong foundation for more advanced mathematical concepts.
Here are some additional resources to further enhance your learning:
By exploring these resources, you can deepen your understanding and gain more insights into solving square roots. Continue to challenge yourself with practice problems and explore various methods to find the ones that work best for you. Happy calculating!
Hướng dẫn cách tìm căn bậc hai bằng tay mà không cần máy tính. Video này giúp bạn hiểu rõ các bước chi tiết và dễ dàng áp dụng.
Tìm Căn Bậc Hai Bằng Tay mà Không Cần Máy Tính
READ MORE:
Hướng dẫn cách tính căn bậc hai bằng tay cho học sinh tiểu học. Video này giúp các em hiểu rõ các bước cơ bản và dễ dàng áp dụng.
Tính Căn Bậc Hai Bằng Tay (Dành Cho Học Sinh Tiểu Học)