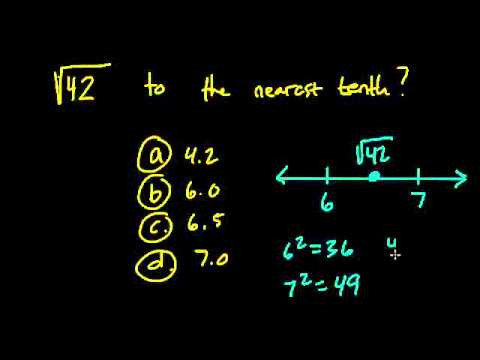Topic simplifying square root calculator: Welcome to our comprehensive guide on simplifying square roots. Discover how to use a square root calculator effectively and learn step-by-step techniques for simplifying complex square roots. This guide is perfect for anyone looking to master the art of simplifying square roots, whether for academic purposes or everyday use.
Table of Content
- Square Root Calculator
- Introduction
- Understanding Square Roots
- How to Simplify Square Roots
- Using a Square Root Calculator
- Examples of Simplifying Square Roots
- Simplifying Square Roots with Prime Factorization
- Handling Non-Perfect Squares
- Simplifying Square Roots of Fractions
- Simplifying Square Roots of Negative Numbers
- Advanced Square Root Simplifications
- Common Mistakes and How to Avoid Them
- Practical Applications of Simplified Square Roots
- Conclusion
- YOUTUBE: Xem video 'Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hóa Radicals' để học cách đơn giản hóa các biểu thức căn bậc hai một cách dễ dàng và hiệu quả.
Square Root Calculator
Welcome to our comprehensive guide on simplifying square roots using our square root calculator. This tool is designed to help you reduce any square root to its simplest radical form and provide step-by-step solutions.
How to Use the Calculator
Simply enter a number in the input box and press "Simplify". The calculator will show the simplest form of the square root along with the steps taken to achieve the result.
Features
- Calculates the principal square root of any real number.
- Handles positive and negative inputs, providing complex solutions for negative numbers.
- Displays both the positive and negative roots for positive real numbers.
- Identifies perfect squares and provides rational or irrational number results.
Examples
| Input | Square Root |
|---|---|
| 81 | \(\sqrt{81} = \pm 9\) |
| 25 | \(\sqrt{25} = \pm 5\) |
| 100 | \(\sqrt{100} = \pm 10\) |
| 10 | \(\sqrt{10} \approx \pm 3.162\) |
Step-by-Step Simplification Process
- Identify the radical expression and check for multiple radicals.
- Group radicals using the rule \(\sqrt{x} \cdot \sqrt{y} = \sqrt{xy}\).
- Simplify the expression under the radical, if possible.
- Use prime factorization to identify perfect square factors.
- Take the square root of any perfect square factors out of the radical.
Square Root Rules
- \(\sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}}\)
- If \(a^2\) is a perfect square factor of the radicand \(x\), then \(\sqrt{a^2 \cdot b} = a \cdot \sqrt{b}\).
Perfect Squares
A number is a perfect square if its square root is an integer. For example, 4, 9, and 16 are perfect squares because their square roots (2, 3, and 4, respectively) are integers.
Additional Information
- A perfect square factor can be taken out of the square root.
- Any factor with an even power in the prime factorization is a perfect square.
- Factors with odd powers can be partially taken out of the square root.
Explore the beauty of mathematics with our square root calculator and gain a deeper understanding of simplifying radicals.

READ MORE:
Introduction
Simplifying square roots is a fundamental skill in mathematics that can help solve various algebraic and geometric problems. A square root calculator is a powerful tool that assists in finding the principal square root of any real number, whether positive or negative. This guide will walk you through the process of simplifying square roots, using both manual methods and calculators, to ensure you have a comprehensive understanding.
Using a square root calculator can simplify complex expressions involving square roots, providing step-by-step solutions and reducing any square root to its simplest radical form. For example, the square root of 8 can be simplified manually as follows:
- First, factorize the number under the root: \( \sqrt{8} = \sqrt{4 \times 2} \)
- Next, separate the factors under the square root: \( \sqrt{4} \times \sqrt{2} \)
- Finally, simplify the perfect square: \( 2\sqrt{2} \)
In addition to manual methods, a square root calculator automates these steps, providing accurate and quick results. Whether you're dealing with perfect squares, non-perfect squares, or even fractions and negative numbers, the calculator can handle it all.
Understanding how to use these tools effectively will enhance your mathematical proficiency and enable you to tackle a wide range of problems with confidence.
Understanding Square Roots
Square roots are fundamental in mathematics, representing a value that, when multiplied by itself, gives the original number. For instance, the square root of 25 is 5, as \(5 \times 5 = 25\). Here, we'll explore the concept of square roots and their properties.
Consider the number 16. The square root of 16 is denoted as \( \sqrt{16} \) and equals 4 because \(4^2 = 16\). Square roots are often used to simplify expressions, solve equations, and in various applications in geometry and algebra.
Properties of Square Roots
- Positive Numbers: For any positive number \(a\), the square root is a positive number \( \sqrt{a} \).
- Multiplication: The square root of a product is the product of the square roots: \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \).
- Division: The square root of a quotient is the quotient of the square roots: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Examples
Here are some examples to illustrate these properties:
| Expression | Simplified Form |
|---|---|
| \( \sqrt{36} \) | 6 |
| \( \sqrt{45} \) | \( \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \) |
| \( \sqrt{\frac{16}{4}} \) | \( \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2 \) |
Handling Non-Perfect Squares
Not all numbers are perfect squares. For example, \( \sqrt{20} \) is not an integer. However, we can simplify it:
\( \sqrt{20} = \sqrt{4 \times 5} = \sqrt{4} \times \sqrt{5} = 2\sqrt{5} \).
This simplification is essential in many mathematical problems and helps in understanding the properties and applications of square roots more deeply.
How to Simplify Square Roots
Simplifying square roots involves reducing the expression to its simplest radical form. Here is a step-by-step guide to help you simplify square roots effectively:
-
Identify the Radicand: The radicand is the number inside the square root symbol. For example, in \( \sqrt{50} \), the radicand is 50.
-
Prime Factorization: Break down the radicand into its prime factors. For 50, the prime factorization is \( 50 = 2 \times 5^2 \).
-
Pair the Factors: Group the prime factors into pairs. In \( 2 \times 5^2 \), we have one pair of 5s.
-
Take Out the Pairs: For every pair of identical factors, take one factor out of the square root. Here, \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \).
-
Simplify the Expression: Multiply any factors outside the square root and simplify the remaining expression. Therefore, \( 5\sqrt{2} \) is the simplified form of \( \sqrt{50} \).
Let's consider another example to reinforce the concept:
- Example: Simplify \( \sqrt{72} \).
- Step 1: Prime factorization: \( 72 = 2^3 \times 3^2 \).
- Step 2: Group the factors: \( 2^3 \) and \( 3^2 \).
- Step 3: Take out the pairs: \( \sqrt{72} = \sqrt{2^3 \times 3^2} = 3\sqrt{2^3} \).
- Step 4: Simplify: \( 3\sqrt{2^3} = 3 \times 2\sqrt{2} = 6\sqrt{2} \).
By following these steps, you can simplify any square root to its simplest radical form efficiently.
Using a Square Root Calculator
Using a square root calculator can greatly simplify the process of finding square roots, especially for complex numbers or large values. Here is a step-by-step guide on how to use a square root calculator:
- Enter the Number: Start by entering the number for which you want to calculate the square root. Most calculators have an input field labeled "Enter the number" or something similar. Simply type in your number.
- Choose the Calculation: Some calculators may offer different operations. Ensure you select the option for calculating the square root, often labeled as "Calculate the Square Root" or similar.
- Submit the Input: After entering the number, click the button to perform the calculation. This button might be labeled "Calculate," "Submit," or have a similar action-oriented label.
- View the Results: The calculator will display the square root of the entered number. The result may be shown in exact form (as a simplified radical) and/or in decimal form, especially if the number is not a perfect square.
- Understand the Output: The calculator might provide additional information such as indicating whether the number is a perfect square, and if it is, both the positive and negative roots. For instance, for the number 25, the output will show that its square roots are \( \pm 5 \).
Using a square root calculator is particularly useful for handling non-perfect squares, simplifying radicals, and solving problems involving square roots of fractions and negative numbers. By following these steps, you can quickly and accurately find the square roots you need.
Here are a few additional tips when using a square root calculator:
- Check for Prime Factorization: Some calculators also provide the option to simplify square roots using prime factorization. This can help in understanding the roots better and in solving mathematical problems.
- Use for Negative Numbers: If dealing with negative numbers, ensure the calculator can handle complex or imaginary numbers. Some calculators will provide results in terms of 'i' for these cases.
- Fractional Inputs: For square roots of fractions, enter the fraction in the input field. The calculator will often simplify the fraction first before finding the square root.
Using a square root calculator effectively can save time and provide accurate results, making it a valuable tool for both students and professionals working with mathematical computations.

Examples of Simplifying Square Roots
Understanding how to simplify square roots is crucial for solving various mathematical problems. Let's look at some detailed examples to illustrate the simplification process step-by-step.
Example 1: Simplifying \(\sqrt{72}\)
- Find the prime factorization of 72: \(72 = 2 \times 2 \times 2 \times 3 \times 3\)
- Group the factors into pairs: \(72 = (2 \times 2) \times (3 \times 3) \times 2\)
- Take one number from each pair out of the square root: \(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \sqrt{2}\)
- Simplify: \(\sqrt{72} = 6\sqrt{2}\)
Example 2: Simplifying \(\sqrt{200}\)
- Find the prime factorization of 200: \(200 = 2 \times 2 \times 2 \times 5 \times 5\)
- Group the factors into pairs: \(200 = (2 \times 2) \times (5 \times 5) \times 2\)
- Take one number from each pair out of the square root: \(\sqrt{200} = \sqrt{(2 \times 2) \times (5 \times 5) \times 2} = 2 \times 5 \sqrt{2}\)
- Simplify: \(\sqrt{200} = 10\sqrt{2}\)
Example 3: Simplifying \(\sqrt{180}\)
- Find the prime factorization of 180: \(180 = 2 \times 2 \times 3 \times 3 \times 5\)
- Group the factors into pairs: \(180 = (2 \times 2) \times (3 \times 3) \times 5\)
- Take one number from each pair out of the square root: \(\sqrt{180} = \sqrt{(2 \times 2) \times (3 \times 3) \times 5} = 2 \times 3 \sqrt{5}\)
- Simplify: \(\sqrt{180} = 6\sqrt{5}\)
Example 4: Simplifying \(\sqrt{48}\)
- Find the prime factorization of 48: \(48 = 2 \times 2 \times 2 \times 2 \times 3\)
- Group the factors into pairs: \(48 = (2 \times 2) \times (2 \times 2) \times 3\)
- Take one number from each pair out of the square root: \(\sqrt{48} = \sqrt{(2 \times 2) \times (2 \times 2) \times 3} = 2 \times 2 \sqrt{3}\)
- Simplify: \(\sqrt{48} = 4\sqrt{3}\)
Example 5: Simplifying \(\sqrt{50}\)
- Find the prime factorization of 50: \(50 = 2 \times 5 \times 5\)
- Group the factors into pairs: \(50 = 2 \times (5 \times 5)\)
- Take one number from the pair out of the square root: \(\sqrt{50} = \sqrt{2 \times (5 \times 5)} = 5\sqrt{2}\)
- Simplify: \(\sqrt{50} = 5\sqrt{2}\)
These examples show the process of simplifying square roots by finding the prime factorization, grouping the factors into pairs, and taking one number from each pair out of the square root. Practice these steps with different numbers to become proficient in simplifying square roots.
Simplifying Square Roots with Prime Factorization
The prime factorization method is a reliable way to simplify square roots, making the process easier and more structured. Here’s a detailed, step-by-step guide to simplify square roots using prime factorization:
-
Factorize the Number: Begin by breaking down the number inside the square root into its prime factors. For instance, let’s take the number 72.
\[ 72 = 2 \times 2 \times 2 \times 3 \times 3 \]
-
Group the Prime Factors: Next, pair the prime factors. Each pair of prime factors will come out of the square root as a single number.
\[ \sqrt{72} = \sqrt{2 \times 2 \times 2 \times 3 \times 3} = \sqrt{(2 \times 2) \times 2 \times (3 \times 3)} \]
-
Take Out the Pairs: For every pair of prime factors, take one factor out of the square root.
\[ \sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \]
Let’s consider more examples to understand this method better:
Example 1: Simplify \(\sqrt{50}\)
Factorize 50 into its prime factors:
\[ 50 = 2 \times 5 \times 5 \]
Group the prime factors:
\[ \sqrt{50} = \sqrt{2 \times (5 \times 5)} \]
Take out the pairs:
\[ \sqrt{50} = 5\sqrt{2} \]
Example 2: Simplify \(\sqrt{200}\)
Factorize 200 into its prime factors:
\[ 200 = 2 \times 2 \times 2 \times 5 \times 5 \]
Group the prime factors:
\[ \sqrt{200} = \sqrt{(2 \times 2) \times 2 \times (5 \times 5)} \]
Take out the pairs:
\[ \sqrt{200} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2} \]
This method can be used for any number, providing a systematic approach to simplifying square roots. By understanding and applying these steps, you can confidently simplify square roots using prime factorization.
Handling Non-Perfect Squares
Simplifying non-perfect square roots can be more challenging compared to perfect squares, but it's achievable through systematic methods. Here's a detailed step-by-step process:
- Identify the Non-Perfect Square:
Consider a non-perfect square number such as \(45\).
- Find the Prime Factorization:
Break down the number into its prime factors.
\[45 = 3^2 \times 5\]
- Pair the Prime Factors:
Group the prime factors into pairs. Each pair of the same number will come out of the square root as a single number.
\[ \sqrt{45} = \sqrt{3^2 \times 5} = 3\sqrt{5} \]
- Simplify:
The simplified form of \(\sqrt{45}\) is \(3\sqrt{5}\).
Let’s consider another example to further clarify this process:
- Example: Simplify \(\sqrt{72}\)
- Prime Factorization:
First, factorize 72 into prime factors.
\[72 = 2^3 \times 3^2\]
- Pair the Prime Factors:
Identify the pairs of prime factors.
\[ \sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 3^2) \times 2} = 6\sqrt{2} \]
- Simplify:
The simplified form of \(\sqrt{72}\) is \(6\sqrt{2}\).
Using a calculator for non-perfect squares involves the same understanding but helps in quickly finding the decimal approximation of the square root. For instance:
- Enter the number (e.g., 72) into the calculator.
- Press the square root (√) function key.
- The calculator will display the decimal value, which is approximately 8.485.
To summarize, simplifying non-perfect squares involves prime factorization and pairing of factors, while a calculator can provide quick decimal approximations for practical use.
Simplifying Square Roots of Fractions
Simplifying square roots of fractions involves two main steps: simplifying the square roots and rationalizing the denominator. Here's a detailed step-by-step guide to help you through the process:
-
Step 1: Simplify the Square Root
Simplify any square roots in the numerator and the denominator. This often involves breaking down the square root into smaller factors. For example:
- \(\sqrt{\frac{18}{50}} = \frac{\sqrt{18}}{\sqrt{50}} = \frac{\sqrt{9 \cdot 2}}{\sqrt{25 \cdot 2}} = \frac{3\sqrt{2}}{5\sqrt{2}} = \frac{3}{5}\)
- \(\sqrt{\frac{32}{18}} = \frac{\sqrt{32}}{\sqrt{18}} = \frac{\sqrt{16 \cdot 2}}{\sqrt{9 \cdot 2}} = \frac{4\sqrt{2}}{3\sqrt{2}} = \frac{4}{3}\)
-
Step 2: Rationalize the Denominator
Remove any square roots from the denominator by multiplying both the numerator and the denominator by the conjugate of the denominator. For example:
- \(\frac{5}{\sqrt{3}} = \frac{5}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}\)
- \(\frac{2}{\sqrt{12}} = \frac{2}{\sqrt{12}} \cdot \frac{\sqrt{12}}{\sqrt{12}} = \frac{2\sqrt{12}}{12} = \frac{\sqrt{3}}{3}\)
Let's look at some additional examples:
| Example 1: | \(\frac{\sqrt{18}}{3}\) | Simplify \(\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\) | Result: \(\frac{3\sqrt{2}}{3} = \sqrt{2}\) |
| Example 2: | \(\frac{2}{\sqrt{12}}\) | Simplify \(\sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}\) | Rationalize: \(\frac{2\sqrt{3}}{12} = \frac{\sqrt{3}}{3}\) |
| Example 3: | \(\frac{\sqrt{6}}{\sqrt{2}}\) | Simplify: \(\sqrt{6} = \sqrt{2 \cdot 3} = \sqrt{2} \cdot \sqrt{3}\) | Result: \(\frac{\sqrt{2} \cdot \sqrt{3}}{\sqrt{2}} = \sqrt{3}\) |
With practice, simplifying square roots of fractions becomes straightforward. Remember to always simplify the square roots first and then rationalize the denominator if needed. This approach ensures your final answer is in its simplest form.
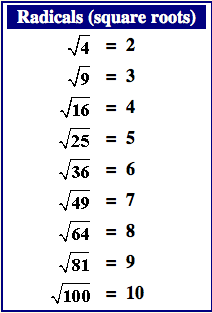
Simplifying Square Roots of Negative Numbers
Simplifying the square root of a negative number involves understanding imaginary numbers. The imaginary unit \(i\) is defined as the square root of -1. Thus, the square root of any negative number can be expressed in terms of \(i\).
- Identify the Negative Square Root:
For example, consider \(\sqrt{-9}\).
- Express the Negative Inside the Radicand:
Rewrite the negative number as the product of -1 and a positive number:
\(\sqrt{-9} = \sqrt{-1 \cdot 9}\)
- Separate the Radicand:
Use the property of square roots to separate the negative and positive parts:
\(\sqrt{-1 \cdot 9} = \sqrt{-1} \cdot \sqrt{9}\)
- Replace \(\sqrt{-1}\) with \(i\):
Since \(\sqrt{-1} = i\), the expression becomes:
\(\sqrt{-1} \cdot \sqrt{9} = i \cdot \sqrt{9}\)
- Simplify the Positive Square Root:
Find the square root of the positive number:
\(i \cdot \sqrt{9} = i \cdot 3 = 3i\)
Therefore, \(\sqrt{-9} = 3i\).
Here are a few more examples:
- \(\sqrt{-16}\):
\(\sqrt{-16} = \sqrt{-1 \cdot 16} = \sqrt{-1} \cdot \sqrt{16} = i \cdot 4 = 4i\)
- \(\sqrt{-25}\):
\(\sqrt{-25} = \sqrt{-1 \cdot 25} = \sqrt{-1} \cdot \sqrt{25} = i \cdot 5 = 5i\)
- \(\sqrt{-48}\):
\(\sqrt{-48} = \sqrt{-1 \cdot 48} = \sqrt{-1} \cdot \sqrt{48} = i \cdot \sqrt{48}\)
Further simplification gives:
\(i \cdot \sqrt{16 \cdot 3} = i \cdot \sqrt{16} \cdot \sqrt{3} = i \cdot 4 \cdot \sqrt{3} = 4i \sqrt{3}\)
In general, the formula for simplifying the square root of any negative number \(-a\) is:
\(\sqrt{-a} = i \sqrt{a}\)
Advanced Square Root Simplifications
Advanced square root simplifications involve techniques that go beyond basic methods, often incorporating algebraic manipulations and properties of exponents. Here are some advanced strategies:
1. Simplifying Nested Radicals
Nested radicals occur when a square root contains another square root inside it. To simplify, follow these steps:
- Identify the nested radical expression, such as \(\sqrt{5 + 2\sqrt{6}}\).
- Assume the expression equals a simple form \(\sqrt{a} + \sqrt{b}\).
- Square both sides to eliminate the outer square root:
\((\sqrt{a} + \sqrt{b})^2 = a + b + 2\sqrt{ab}\).
- Set the squared expression equal to the original inner term:
\(5 + 2\sqrt{6} = a + b + 2\sqrt{ab}\).
- Solve for \(a\) and \(b\) by comparing coefficients. For instance, if \(a = 2\) and \(b = 3\), the simplified form is:
\(\sqrt{5 + 2\sqrt{6}} = \sqrt{2} + \sqrt{3}\).
2. Rationalizing Complex Denominators
When dealing with complex fractions involving square roots in the denominator, rationalize the denominator using conjugates:
- Given a fraction like \(\frac{1}{\sqrt{2} + \sqrt{3}}\), multiply the numerator and denominator by the conjugate \(\sqrt{2} - \sqrt{3}\):
- \(\frac{1}{\sqrt{2} + \sqrt{3}} \times \frac{\sqrt{2} - \sqrt{3}}{\sqrt{2} - \sqrt{3}} = \frac{\sqrt{2} - \sqrt{3}}{(\sqrt{2})^2 - (\sqrt{3})^2} = \frac{\sqrt{2} - \sqrt{3}}{2 - 3} = \frac{\sqrt{2} - \sqrt{3}}{-1} = -\sqrt{2} + \sqrt{3}\).
3. Exponential and Logarithmic Manipulations
Square roots can be expressed using exponents and manipulated using properties of exponents and logarithms:
- Convert square roots to fractional exponents: \(\sqrt{x} = x^{1/2}\).
- Use properties of exponents to simplify expressions, such as \(x^{1/2} \cdot x^{1/3} = x^{(1/2 + 1/3)} = x^{5/6}\).
- Apply logarithms for more complex expressions:
\(\log(\sqrt{x}) = \log(x^{1/2}) = \frac{1}{2}\log(x)\).
4. Utilizing Trigonometric Identities
In some advanced applications, trigonometric identities can simplify expressions involving square roots:
- Use identities such as \(\sin^2(\theta) + \cos^2(\theta) = 1\) to simplify expressions.
- Example: Simplify \(\sqrt{1 - \sin^2(\theta)} = \cos(\theta)\).
By mastering these advanced techniques, you can simplify complex square root expressions effectively, making calculations more manageable and expressions more elegant.
Common Mistakes and How to Avoid Them
When simplifying square roots, it's crucial to avoid common mistakes to ensure accurate results. Here are some typical errors and tips on how to steer clear of them:
-
Ignoring Prime Factorization:
Prime factorization is a fundamental step in simplifying square roots. Skipping this step can lead to incomplete or incorrect simplification. Always fully factor the radicand into its prime factors.
-
Misidentifying Perfect Squares:
Confusing perfect and non-perfect squares can significantly impact the simplification process. Ensure to correctly identify and separate perfect squares from non-perfect ones.
-
Incorrectly Simplifying Variables:
When variables are involved, it is essential to apply the correct rules. Remember that the square root of a variable raised to an even power simplifies to the variable raised to half that power (e.g., \(\sqrt{x^2} = x\)). Incorrect application of these rules can result in errors.
-
Overlooking Rationalization:
Failing to rationalize the denominator when required is a common oversight. Always multiply the numerator and the denominator by the square root present in the denominator to eliminate it and ensure the expression is simplified correctly.
-
Miscalculating with Non-Perfect Squares:
Approximating non-perfect squares without proper verification can lead to inaccuracies. Always double-check your work to ensure the simplification is accurate.
-
Forgetting the Absolute Value:
When simplifying expressions with variables, it is important to include absolute value signs when necessary to maintain the correctness of the solution, especially when dealing with even powers of variables.
By being mindful of these common mistakes and applying careful, systematic strategies, you can improve your proficiency in simplifying square roots and avoid common pitfalls. Practice regularly and seek help when needed to further enhance your skills.
Practical Applications of Simplified Square Roots
Simplified square roots have numerous practical applications across various fields. Understanding these applications can provide insights into the importance and utility of square roots in real-world scenarios.
1. Finance
In finance, square roots are used to calculate stock market volatility, which measures how much a stock’s price varies over time. By taking the square root of the variance in returns, investors can assess the risk associated with a particular investment.
2. Architecture
Architects and engineers use square roots to determine the natural frequency of structures such as bridges and buildings. This helps in predicting how structures will respond to different loads, such as wind or traffic, ensuring their stability and safety.
3. Science
Square roots are essential in various scientific calculations, including determining the velocity of moving objects, the amount of radiation absorbed by materials, and the intensity of sound waves. These calculations help scientists understand natural phenomena and develop new technologies.
4. Statistics
In statistics, square roots are used to calculate standard deviation, a measure of how much data points deviate from the mean. This is crucial for data analysis, helping statisticians make informed decisions based on data variability.
5. Geometry
Square roots are fundamental in geometry for calculating the area and perimeter of shapes, especially when solving problems involving right triangles. The Pythagorean theorem, which involves square roots, is a key tool in these calculations.
6. Computer Science
In computer science, square roots are used in algorithms for encryption, image processing, and game physics. For instance, encryption algorithms often use square roots to generate secure keys for data transmission.
7. Navigation
Square roots help in navigation by calculating distances between points on maps or globes. Pilots use these calculations to determine flight paths and distances between destinations, ensuring accurate and efficient travel.
8. Electrical Engineering
Electrical engineers use square roots to compute power, voltage, and current in circuits. These calculations are critical for designing and developing electrical systems, including power grids and communication networks.
9. Photography
In photography, the f-number, which controls the amount of light entering the camera, is related to the square root of the aperture area. This relationship helps photographers adjust exposure settings for optimal image quality.
10. Cooking
Recipes often require scaling ingredients, and square roots are used to adjust quantities while maintaining the correct proportions. This ensures that the flavor and texture of dishes remain consistent when making larger or smaller batches.
11. Computer Graphics
Square roots are used in computer graphics to calculate distances between points and lengths of vectors. These calculations are essential for rendering accurate 2D and 3D graphics in various applications, from video games to simulations.
These examples illustrate the diverse and significant roles that simplified square roots play in various fields, highlighting their practical importance and widespread utility.

Conclusion
Simplifying square roots can initially seem challenging, but with practice and the use of a reliable square root calculator, it becomes a straightforward task. The key steps involve understanding the properties of square roots, recognizing perfect squares, and applying the rules of simplification consistently.
By using prime factorization, identifying pairs of factors, and breaking down complex expressions, you can simplify most square roots to their simplest forms. This process not only helps in solving mathematical problems more efficiently but also enhances your overall understanding of algebra and number theory.
Utilizing a square root calculator, such as those available on Symbolab or MathCracker, can greatly assist in visualizing the step-by-step process of simplification. These tools provide a detailed breakdown of each step, ensuring that you understand the logic behind the simplification and can apply it to other problems in the future.
Remember, the ultimate goal of simplifying square roots is to make expressions easier to work with, whether for solving equations, performing further calculations, or simply for clarity. With the right approach and tools, anyone can master the art of simplifying square roots, leading to greater confidence and competence in mathematical tasks.
In summary, the practice of simplifying square roots is a valuable skill that offers numerous benefits in mathematical problem-solving. By breaking down complex expressions into their simplest forms, you can gain a deeper understanding and appreciation of mathematics. So, keep practicing, use the available tools, and enjoy the process of simplifying square roots!
Xem video 'Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hóa Radicals' để học cách đơn giản hóa các biểu thức căn bậc hai một cách dễ dàng và hiệu quả.
Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hóa Radicals
READ MORE:
Xem video 'Đơn Giản Hóa Căn Bậc Hai Với Máy Tính Đồ Thị' để học cách sử dụng máy tính đồ thị để đơn giản hóa các biểu thức căn bậc hai một cách hiệu quả.
Đơn Giản Hóa Căn Bậc Hai Với Máy Tính Đồ Thị