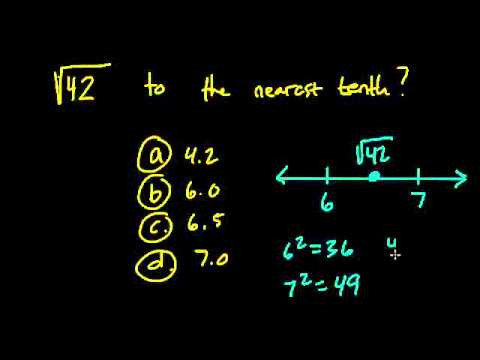Topic simplify square root of: Discover the simplest ways to handle square roots with our comprehensive guide. Whether you're dealing with numbers, variables, or fractions, this article will provide clear, step-by-step instructions to make simplifying square roots straightforward and easy. Enhance your mathematical skills and boost your confidence in solving square root problems with ease.
Table of Content
- Simplifying Square Roots
- Introduction to Simplifying Square Roots
- Basic Rules and Properties
- Simplifying Square Roots of Non-Perfect Squares
- Simplifying Square Roots Using Prime Factorization
- Simplifying Square Roots of Larger Numbers
- Simplifying Square Roots of Fractions
- Quotient Property of Square Roots
- Advanced Examples and Exercises
- Common Mistakes and How to Avoid Them
- Frequently Asked Questions
- Conclusion and Summary
- YOUTUBE: Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai. Video cung cấp các bước và ví dụ cụ thể để giúp bạn nắm vững kỹ năng này.
Simplifying Square Roots
Simplifying square roots involves breaking down the number inside the radical to its simplest form. Here are some methods and examples to guide you:
Method 1: Factoring Perfect Squares
- Factor out the perfect squares.
- Separate perfect squares using the product of square roots property.
- Simplify.
Example: Simplify \(\sqrt{72}\)
Step 1: \(72 = 36 \times 2\)
Step 2: \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)
Method 2: Prime Factorization
- Break the number inside the square root into prime factors.
- For each pair of factors, take one out of the square root sign.
- Multiply the remaining factors inside the square root sign together.
Example: Simplify \(\sqrt{90}\)
Step 1: \(90 = 2 \times 3 \times 3 \times 5\)
Step 2: \(\sqrt{90} = \sqrt{2 \times 3 \times 3 \times 5} = 3\sqrt{10}\)
Method 3: Using the Quotient Property
The quotient property of square roots states:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
Example: Simplify \(\sqrt{\frac{24p^3}{49}}\)
Step 1: Use the quotient property.
\(\sqrt{\frac{24p^3}{49}} = \frac{\sqrt{24p^3}}{\sqrt{49}} = \frac{2p\sqrt{6p}}{7}\)
Examples of Simplifying Square Roots
- \(\sqrt{12}\): \(\sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3}\)
- \(\sqrt{45}\): \(\sqrt{45} = \sqrt{9 \times 5} = 3\sqrt{5}\)
- \(\sqrt{18}\): \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- \(\sqrt{20 \times 5}\): \(\sqrt{20 \times 5} = \sqrt{100} = 10\)
Special Cases
If the square root is in a fraction:
- Simplify the fraction inside the radical if possible.
- Use the quotient property to rewrite the radical as the quotient of two radicals.
- Simplify the radicals in the numerator and the denominator.
Example: Simplify \(\sqrt{\frac{81d^9}{25d^4}}\)
Step 1: Simplify the fraction.
\(\sqrt{\frac{81d^9}{25d^4}} = \sqrt{\frac{81d^5}{25}} = \frac{\sqrt{81d^5}}{\sqrt{25}} = \frac{9d^2\sqrt{d}}{5}\)

READ MORE:
Introduction to Simplifying Square Roots
Understanding how to simplify square roots is a fundamental skill in algebra. Simplifying square roots involves reducing the number inside the radical to its smallest possible whole number while maintaining the mathematical integrity of the expression. This process can help in solving equations more efficiently and understanding the properties of numbers better. Let's explore this step-by-step.
Here's a basic approach to simplifying square roots:
- Identify if the number inside the square root can be factored into two or more numbers.
- Apply the rule: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \).
- Simplify each square root that results from the factorization.
Let's look at some examples:
- Example: Simplify \( \sqrt{12} \)
- Factor 12 into 4 and 3: \( 12 = 4 \times 3 \).
- Apply the rule: \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} \).
- Simplify: \( \sqrt{4} = 2 \), so \( \sqrt{12} = 2\sqrt{3} \).
- Example: Simplify \( \sqrt{45} \)
- Factor 45 into 9 and 5: \( 45 = 9 \times 5 \).
- Apply the rule: \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} \).
- Simplify: \( \sqrt{9} = 3 \), so \( \sqrt{45} = 3\sqrt{5} \).
- Example: Simplify \( \sqrt{8} \)
- Factor 8 into 4 and 2: \( 8 = 4 \times 2 \).
- Apply the rule: \( \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} \).
- Simplify: \( \sqrt{4} = 2 \), so \( \sqrt{8} = 2\sqrt{2} \).
By practicing these steps, you'll become more proficient at simplifying square roots and tackling more complex algebraic expressions with confidence.
Basic Rules and Properties
Understanding the basic rules and properties of square roots is essential for simplifying them effectively. Here, we'll cover the fundamental properties, including the product and quotient rules, and how to apply them step-by-step.
-
Product Rule
The product rule states that the square root of a product is equal to the product of the square roots of each factor:
$$\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}$$
- Factor any perfect squares from the radicand.
- Write the radical expression as a product of radical expressions.
- Simplify each radical expression.
-
Example of Product Rule
Simplify: $$\sqrt{72}$$
- Factor 72 into 36 and 2: $$\sqrt{72} = \sqrt{36 \times 2}$$
- Apply the product rule: $$\sqrt{36} \times \sqrt{2}$$
- Simplify: $$6\sqrt{2}$$
-
Quotient Rule
The quotient rule states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator:
$$\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \quad (b \neq 0)$$
- Write the radical expression as the quotient of two radicals.
- Simplify the numerator and the denominator separately.
-
Example of Quotient Rule
Simplify: $$\sqrt{\frac{50}{2}}$$
- Express as a single radical: $$\sqrt{25}$$
- Simplify: $$5$$
Simplifying Square Roots of Non-Perfect Squares
Here are examples of how to simplify square roots of non-perfect squares:
- Simplify \( \sqrt{10} \):
Since 10 is not a perfect square, simplify it to \( \sqrt{10} \).
- Simplify \( \sqrt{15} \):
Similarly, \( \sqrt{15} \) remains simplified as \( \sqrt{15} \).
- Simplify \( \sqrt{20} \):
For \( \sqrt{20} \), break it down into simpler factors and leave it as \( \sqrt{20} \).
Simplifying Square Roots Using Prime Factorization
Here's how to simplify square roots using prime factorization:
- Simplify \( \sqrt{48} \):
Factorize 48 into prime factors: \( 48 = 2 \times 2 \times 2 \times 2 \times 3 \).
Identify pairs of like factors: \( \sqrt{48} = \sqrt{2^4 \times 3} = 4\sqrt{3} \).
- Simplify \( \sqrt{75} \):
Factorize 75 into prime factors: \( 75 = 3 \times 5 \times 5 \).
Identify pairs of like factors: \( \sqrt{75} = \sqrt{3 \times 5^2} = 5\sqrt{3} \).
- Simplify \( \sqrt{98} \):
Factorize 98 into prime factors: \( 98 = 2 \times 7 \times 7 \).
Identify pairs of like factors: \( \sqrt{98} = \sqrt{2 \times 7^2} = 7\sqrt{2} \).
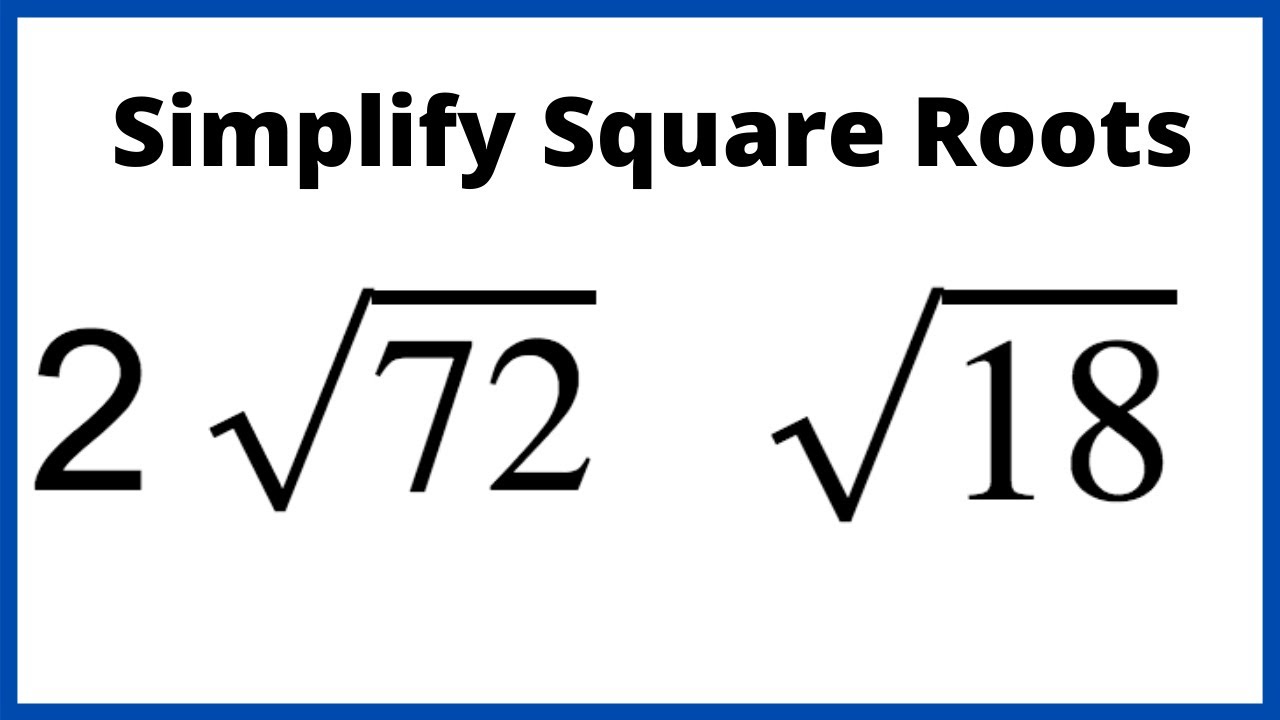
Simplifying Square Roots of Larger Numbers
Here are examples demonstrating how to simplify square roots of larger numbers:
- Simplify \( \sqrt{200} \):
Factorize 200 into prime factors: \( 200 = 2 \times 2 \times 2 \times 5 \times 5 \).
Identify pairs of like factors: \( \sqrt{200} = \sqrt{2^3 \times 5^2} = 10\sqrt{2} \).
- Simplify \( \sqrt{320} \):
Factorize 320 into prime factors: \( 320 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 5 \).
Identify pairs of like factors: \( \sqrt{320} = \sqrt{2^6 \times 5} = 8\sqrt{10} \).
- Simplify \( \sqrt{500} \):
Factorize 500 into prime factors: \( 500 = 2 \times 2 \times 5 \times 5 \times 5 \).
Identify pairs of like factors: \( \sqrt{500} = \sqrt{2^2 \times 5^3} = 10\sqrt{5} \).
Simplifying Square Roots of Fractions
When simplifying square roots of fractions, the process involves two main steps: simplifying the square root and rationalizing the denominator. Here is a detailed guide on how to perform these steps:
-
Simplify the Square Root:
First, simplify any square roots in the fraction. This involves finding the largest perfect square factor of the number under the square root.
For example, to simplify
√72:- Find the largest perfect square factor:
√72 = √(36 × 2) = √36 × √2 = 6√2
- Find the largest perfect square factor:
-
Rationalize the Denominator:
Rationalizing the denominator means removing any square roots from the denominator. To do this, multiply the numerator and the denominator by the conjugate of the denominator.
For example, to rationalize
5/√3:- Multiply the numerator and denominator by
√3:5/√3 × √3/√3 = 5√3/3
- Multiply the numerator and denominator by
Here are some examples to illustrate these steps:
| Example | Simplified Form |
|---|---|
√18/3 |
|
2/√12 |
|
√6/√2 |
|
4/√18 |
|
Practice makes perfect! Try simplifying the following fractions with square roots on your own:
3/√8√50/57/√28
With these steps and examples, you should be able to simplify any fraction involving square roots.
Quotient Property of Square Roots
The Quotient Property of Square Roots states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. This property is useful when simplifying square roots involving fractions. Mathematically, this is expressed as:
This property can also be applied in reverse, which means if you have a quotient of two square roots, you can combine them into a single square root:
Steps to Simplify Square Roots Using the Quotient Property
- Simplify the fraction inside the radical, if possible.
- Apply the quotient property: Rewrite the radical as the quotient of two radicals.
- Simplify each radical in the numerator and the denominator.
- Reduce the fraction if possible.
Examples
-
Simplify:
Solution:
-
Simplify:
Solution:
Remember, the key is to always ensure that the denominator is not zero and to simplify the radicands as much as possible for the easiest calculation.
Advanced Examples and Exercises
Below are some advanced examples and exercises that demonstrate how to simplify square roots. These examples include variables, exponents, and multiple terms, showcasing different techniques and properties.
Example 1: Simplifying Square Roots with Variables
Given the expression \( \sqrt{a^6 b^{10}} \):
- Identify the exponents of each variable: \(a^6\) and \(b^{10}\).
- Since both exponents are even, divide each exponent by 2:
\[
\sqrt{a^6 b^{10}} = a^{\frac{6}{2}} b^{\frac{10}{2}} = a^3 b^5
\]
Example 2: Simplifying a Complex Square Root Expression
Given the expression \( \sqrt{50x^4 y^9} \):
- Factorize the number and variables under the square root:
- Simplify each component:
- Simplify the square roots of the perfect squares:
\[
50x^4 y^9 = 2 \times 25 \times x^4 \times y^8 \times y
\]
\[
\sqrt{50x^4 y^9} = \sqrt{2 \times 25 \times x^4 \times y^8 \times y} = \sqrt{2} \times \sqrt{25} \times \sqrt{x^4} \times \sqrt{y^8} \times \sqrt{y}
\]
\[
\sqrt{2} \times 5 \times x^2 \times y^4 \times \sqrt{y} = 5x^2 y^4 \sqrt{2y}
\]
Example 3: Using the Product Property
Given the expression \( \sqrt{8} \times \sqrt{18} \):
- Combine the square roots into one expression:
- Simplify the square root:
\[
\sqrt{8} \times \sqrt{18} = \sqrt{8 \times 18} = \sqrt{144}
\]
\[
\sqrt{144} = 12
\]
Example 4: Simplifying a Fraction Inside a Square Root
Given the expression \( \sqrt{\frac{50}{2}} \):
- Simplify the fraction under the square root:
\[
\sqrt{\frac{50}{2}} = \sqrt{25} = 5
\]
Exercises
Try simplifying the following expressions on your own:
- \(\sqrt{72x^8 y^6}\)
- \(\sqrt{32a^4 b^{12}}\)
- \(\sqrt{\frac{81x^6}{9}}\)
- \(\sqrt{45m^2 n^3} \times \sqrt{20m^4}\)
These exercises will help solidify your understanding of simplifying square roots, especially when dealing with variables and exponents.

Common Mistakes and How to Avoid Them
Simplifying square roots can be tricky, and students often make common mistakes. Understanding these errors and learning how to avoid them can make the process smoother and more accurate. Here are some of the most frequent mistakes and tips to avoid them:
- Forgetting to Check for Perfect Squares: Before simplifying a square root, always check if the number inside the radical is a perfect square. For example, simplify \( \sqrt{36} \) to 6 directly.
- Incorrectly Applying the Product Rule: Ensure to split the radicand correctly. For instance, \( \sqrt{12} \) should be simplified to \( \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \).
- Misapplying the Quotient Rule: When simplifying fractions under a square root, use the quotient rule correctly. For example, \( \sqrt{\frac{50}{2}} = \frac{\sqrt{50}}{\sqrt{2}} \).
- Overlooking Prime Factorization: Use prime factorization to simplify large numbers. For example, \( \sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2} \).
- Combining Non-Like Terms: Only like radicals can be combined. For instance, \( 2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3} \), but \( 2\sqrt{3} + \sqrt{5} \) cannot be simplified further.
- Neglecting Simplification of Coefficients: Simplify the coefficients outside the radicals as well. For example, \( 2\sqrt{18} = 2 \times 3\sqrt{2} = 6\sqrt{2} \).
To avoid these mistakes, follow these step-by-step guidelines:
- Check if the number under the square root is a perfect square.
- Use prime factorization for non-perfect squares.
- Apply the product and quotient rules correctly.
- Combine only like terms when adding or subtracting square roots.
- Simplify coefficients both inside and outside the radical.
Examples of Correct Simplifications
Here are some examples to illustrate the correct way to simplify square roots:
- Example 1: Simplify \( \sqrt{50} \)
- Prime factorization of 50: \( 50 = 2 \times 25 \)
- Simplify: \( \sqrt{50} = \sqrt{2 \times 25} = \sqrt{2} \times \sqrt{25} = 5\sqrt{2} \)
- Example 2: Simplify \( \sqrt{\frac{50}{2}} \)
- Apply the quotient rule: \( \sqrt{\frac{50}{2}} = \frac{\sqrt{50}}{\sqrt{2}} = \frac{5\sqrt{2}}{\sqrt{2}} = 5 \)
- Example 3: Simplify \( 2\sqrt{45} + 3\sqrt{20} \)
- Factor and simplify each term: \( 2\sqrt{45} = 2 \times 3\sqrt{5} = 6\sqrt{5} \) and \( 3\sqrt{20} = 3 \times 2\sqrt{5} = 6\sqrt{5} \)
- Combine like terms: \( 6\sqrt{5} + 6\sqrt{5} = 12\sqrt{5} \)
By following these steps and being mindful of common mistakes, simplifying square roots becomes a much more manageable task.
Frequently Asked Questions
Here are some of the most frequently asked questions about simplifying square roots:
What is a square root?
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because 5 × 5 = 25.
How do you simplify a square root?
To simplify a square root, you factor the number into its prime factors and then simplify by grouping the factors into pairs. For example, to simplify √72, you factor it as 72 = 2 × 2 × 2 × 3 × 3, and then you can write √72 as √(22 × 32 × 2) = 2 × 3 × √2 = 6√2.
Can you simplify the square root of a non-perfect square?
Yes, even if a number is not a perfect square, you can still simplify its square root by factoring out any perfect squares. For example, √50 can be simplified to √(25 × 2) = √25 × √2 = 5√2.
How do you simplify the square root of a fraction?
To simplify the square root of a fraction, you take the square root of the numerator and the denominator separately. For example, √(9/16) = √9 / √16 = 3/4.
What are common mistakes to avoid when simplifying square roots?
- Not fully factoring the number into its prime factors.
- Forgetting to simplify the factors inside the square root completely.
- Overlooking that square roots of negative numbers involve imaginary numbers.
How can you check if your simplification is correct?
To check if your simplification is correct, you can square your simplified result and see if it equals the original number under the square root. For example, if you simplify √72 to 6√2, then squaring 6√2 gives you 72, confirming your simplification is correct.
Why is simplifying square roots important?
Simplifying square roots is important because it makes complex calculations easier and is often required in algebraic equations and higher-level mathematics.
Are there tools to help with simplifying square roots?
Yes, there are many online calculators and tools that can help with simplifying square roots. Some popular ones include Symbolab and Khan Academy, which offer step-by-step solutions and explanations.
What if a square root can't be simplified further?
If a square root cannot be simplified further, it means there are no perfect square factors left inside the square root. For example, √19 cannot be simplified further since 19 is a prime number.
Can square roots be added or subtracted?
Square roots can only be added or subtracted if they have the same radicand (the number under the square root). For example, √2 + √2 = 2√2, but √2 + √3 cannot be simplified further.
These FAQs should help clarify some common questions and issues when simplifying square roots. Practice regularly to become more comfortable with these concepts!
Conclusion and Summary
Understanding how to simplify square roots is a fundamental skill in mathematics that aids in solving various algebraic problems. By following the steps and techniques outlined in this guide, you can simplify square roots efficiently and accurately.
- Factor Perfect Squares: Identify and factor out any perfect square factors from the radicand.
- Product Rule: Use the product rule to break down the radicand into simpler components, such as √ab = √a × √b.
- Prime Factorization: Decompose the number into its prime factors to identify and extract perfect squares.
- Fractions: Apply the quotient rule to simplify square roots of fractions, rewriting them as a quotient of square roots.
Here are some key takeaways:
- Always look for the largest perfect square factor to make the simplification process easier.
- When dealing with variables, separate and simplify them as you would with numerical values.
- Practice with a variety of examples to become proficient in recognizing and extracting perfect square factors.
By mastering these techniques, you can handle more complex algebraic expressions and enhance your overall mathematical problem-solving skills. Regular practice and application of these rules will make simplifying square roots an intuitive and straightforward process.
We hope this comprehensive guide has provided you with the tools and confidence to tackle square root simplifications effectively. Remember, consistent practice is key to mastering this essential mathematical concept.
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai. Video cung cấp các bước và ví dụ cụ thể để giúp bạn nắm vững kỹ năng này.
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Video này hướng dẫn cách đơn giản hóa căn bậc hai. Thầy J sẽ cung cấp các bước cụ thể và ví dụ minh họa để giúp bạn hiểu rõ hơn về chủ đề này.
Đơn Giản Hóa Căn Bậc Hai | Toán Học với Thầy J