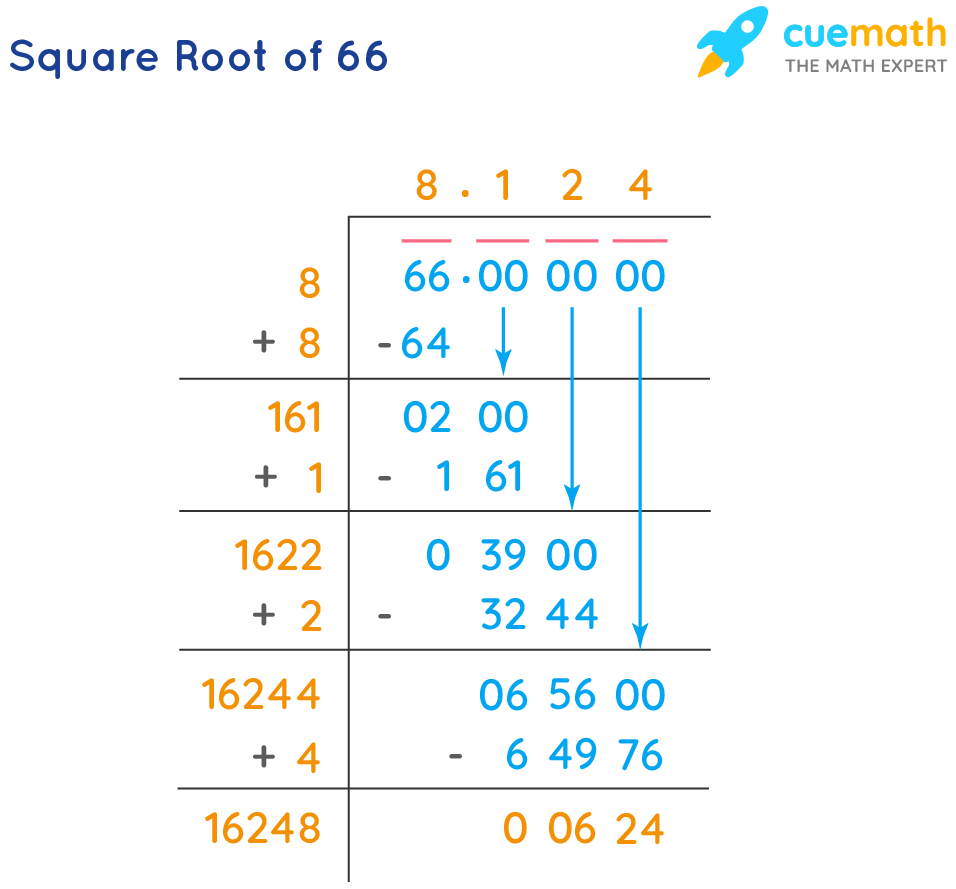
Topic simplifying a square root calculator: Discover the simplicity and efficiency of using a square root calculator to simplify square roots. Our comprehensive guide will walk you through the process, ensuring you understand every step and can confidently simplify any square root. Whether you're a student or just looking to refresh your math skills, this guide is for you!
Table of Content
- Simplifying Square Roots Calculator
- Introduction to Square Roots
- Understanding the Basics of Square Roots
- What is Simplifying Square Roots?
- Steps to Simplify Square Roots
- Understanding Simplification Rules
- Example Calculations
- Step-by-Step Guide to Simplifying Square Roots
- Using a Square Root Calculator
- Manual Calculation vs. Calculator Use
- Examples of Simplifying Square Roots
- Common Mistakes and How to Avoid Them
- Advanced Techniques in Simplifying Radicals
- Applications of Simplified Square Roots
- Frequently Asked Questions
- Additional Resources and Tools
- YOUTUBE: Khám phá cách sử dụng máy tính ClassWiz để đơn giản hóa căn bậc hai một cách hiệu quả trong đại số.
Simplifying Square Roots Calculator
Use our calculator to simplify square roots into their simplest radical form. This tool also provides detailed step-by-step solutions to help you understand the process.
How to Simplify Square Roots
Simplifying square roots involves breaking down the number inside the radical to its prime factors and then extracting any perfect squares.
- Find the prime factorization of the number under the square root.
- Identify and group the factors into pairs.
- Extract the pairs from under the square root as single numbers.
- Multiply any numbers outside the radical together.
Example: Simplifying \( \sqrt{50} \)
- Prime factorization: \( 50 = 2 \times 5^2 \)
- Extract the perfect square: \( \sqrt{50} = 5\sqrt{2} \)
Using the Square Root Calculator
Enter the radicand (the number under the square root) into the calculator and click "Simplify" to see the result along with the detailed steps.
Benefits of Using a Square Root Simplifier
- Quick and accurate simplification of square roots.
- Step-by-step explanations for educational purposes.
- Helps in understanding the properties of radicals.
| Radical Expression | Simplified Form | Steps |
| \( \sqrt{72} \) | \( 6\sqrt{2} \) | Prime factorization: \( 72 = 2^3 \times 3^2 \); Extract pairs: \( 6\sqrt{2} \) |
| \( \sqrt{18} \) | \( 3\sqrt{2} \) | Prime factorization: \( 18 = 2 \times 3^2 \); Extract pairs: \( 3\sqrt{2} \) |
For more complex expressions involving multiple radicals or fractions, our calculator can handle them too, using the following rules:
- \( \sqrt{x} \cdot \sqrt{y} = \sqrt{xy} \)
- \( \frac{\sqrt{x}}{\sqrt{y}} = \sqrt{\frac{x}{y}} \)
Why Simplify Square Roots?
Simplifying square roots is essential for various mathematical applications, including solving equations, simplifying expressions, and reducing complexity in calculations.
Try out the calculator today to simplify any square root expression easily!

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations used to determine a value which, when multiplied by itself, yields the original number. Understanding square roots is essential for various applications in algebra, geometry, and real-world problem-solving.
The symbol for the square root is √, and it is applied to a number known as the radicand. For example, the square root of 25 is written as √25, and its value is 5, since 5 × 5 = 25.
Square roots can be categorized into perfect squares and non-perfect squares. A perfect square is an integer that is the square of another integer, such as 1, 4, 9, 16, etc. Non-perfect squares are numbers that do not have an integer as their square root, such as 2, 3, 5, etc.
Here are some properties of square roots that can be useful:
- Product Property: The square root of a product is the product of the square roots. For example, √(a × b) = √a × √b.
- Quotient Property: The square root of a quotient is the quotient of the square roots. For example, √(a / b) = √a / √b.
- Power Property: The square root of a squared number is the absolute value of the original number. For example, √(a²) = |a|.
To simplify a square root, one can factorize the radicand into its prime factors and then apply the square root to each factor. For instance:
- Factorize the number inside the square root. Example: √50 = √(2 × 5 × 5).
- Group the factors into pairs. In this case, 5 is paired.
- Take the square root of each pair. Here, √(5²) = 5.
- Multiply the results of the pairs outside the square root. So, √50 = 5√2.
Understanding these basics will help you utilize square roots more effectively in various mathematical contexts.
Understanding the Basics of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because \(3 \times 3 = 9\). Square roots are denoted by the radical symbol \(\sqrt{}\). In mathematical terms, the square root of \(x\) is written as \(\sqrt{x}\).
Here are some fundamental properties and rules associated with square roots:
- Non-negative values: The square root function only applies to non-negative numbers. For negative numbers, the result is an imaginary number.
- Perfect squares: Numbers like 1, 4, 9, 16, 25, etc., are perfect squares because their square roots are whole numbers.
Let’s go through some key points to understand square roots better:
- Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\).
- Notation: The square root of \(x\) is denoted as \(\sqrt{x}\).
- Properties:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
Let’s simplify some square roots step-by-step:
| \(\sqrt{12}\) | Identify factors: \(12 = 4 \times 3\) |
| \(\sqrt{12}\) | Use the property: \(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\) |
| \(\sqrt{45}\) | Identify factors: \(45 = 9 \times 5\) |
| \(\sqrt{45}\) | Use the property: \(\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}\) |
These examples demonstrate the simplification process. Identifying perfect square factors within the number under the radical helps in breaking it down to its simplest form. Understanding these basics will make it easier to handle more complex square root problems.
What is Simplifying Square Roots?
Simplifying square roots involves reducing a square root to its simplest radical form. This process can help make calculations easier and expressions more manageable. Here’s a detailed guide to understanding and simplifying square roots:
Steps to Simplify Square Roots
- Identify the radicand:
The radicand is the number inside the square root symbol. For example, in \(\sqrt{18}\), the radicand is 18.
- Find the prime factorization:
Break down the radicand into its prime factors. For 18, the prime factorization is \(2 \times 3^2\).
- Group the prime factors:
Group the prime factors into pairs. In our example, \(3^2\) is a pair.
- Simplify the square root:
For each pair of prime factors, take one factor out of the square root. So, \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\).

Understanding Simplification Rules
- Product Rule: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
This rule allows you to break down a product inside the square root into separate square roots.
- Quotient Rule: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
This rule lets you split a fraction inside the square root into separate square roots for the numerator and the denominator.
Example Calculations
| Expression | Simplified Form |
| \(\sqrt{50}\) | \(5\sqrt{2}\) |
| \(\sqrt{72}\) | \(6\sqrt{2}\) |
By understanding these basic steps and rules, you can simplify any square root. Practice with different numbers to become proficient at simplifying square roots.
Step-by-Step Guide to Simplifying Square Roots
Simplifying square roots involves expressing a square root in its simplest form. This guide will walk you through the process step-by-step, using MathJax for clear mathematical representation.
-
Identify the radicand (the number inside the square root). For example, in \( \sqrt{50} \), the radicand is 50.
-
Factorize the radicand into its prime factors. For 50, the prime factorization is \( 50 = 2 \times 5^2 \).
-
Pair the prime factors. In this case, \( 5^2 \) can be paired as \( (5 \times 5) \).
-
Take one number from each pair out of the square root. Here, one 5 comes out of the square root.
-
Simplify the expression by multiplying the numbers outside the square root and keeping any unpaired factors inside. Thus, \( \sqrt{50} = 5\sqrt{2} \).
Let's break down another example:
Example: Simplify \( \sqrt{72} \)
Prime factorization: \( 72 = 2^3 \times 3^2 \)
Pair the prime factors: \( 2^3 \) has one pair of 2s, and \( 3^2 \) has one pair of 3s.
Take one number from each pair out: \( 2 \times 3 = 6 \).
Keep unpaired factors inside: \( 2 \) remains inside the square root.
Result: \( \sqrt{72} = 6\sqrt{2} \).
For fractions:
Example: Simplify \( \frac{\sqrt{18}}{\sqrt{2}} \)
Combine under a single square root: \( \sqrt{\frac{18}{2}} \)
Simplify the fraction inside: \( \sqrt{9} = 3 \).
Practice with different radicands to master simplifying square roots!
Using a Square Root Calculator
A square root calculator is a powerful tool that helps you simplify square roots and perform complex calculations quickly. Here's a detailed guide on how to use one effectively:
-
Input the Number:
Enter the number you wish to find the square root of into the calculator. For example, to simplify \( \sqrt{50} \), you would input "50".
-
Select the Operation:
Choose the operation you want to perform. Most calculators offer options to find the square root, simplify it, or both.
-
View the Steps:
The calculator will provide a step-by-step breakdown of the simplification process. For instance, for \( \sqrt{50} \):
- Factorize the number under the square root: \( 50 = 2 \times 5^2 \).
- Extract the square factors: \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \).
-
Review the Result:
The final simplified form will be displayed, in this case, \( 5\sqrt{2} \).
-
Additional Features:
Some calculators provide approximations of the square root, handling of complex numbers, and more. For example, entering a negative number would show the result as a complex number.
Using a square root calculator not only speeds up calculations but also helps you understand the process of simplification, ensuring accuracy and efficiency in your math tasks.

Manual Calculation vs. Calculator Use
Understanding the difference between manual calculation and using a square root calculator can help you decide which method to use based on your needs and the complexity of the problem.
Here’s a detailed comparison:
- Manual Calculation:
- Requires a good grasp of mathematical concepts and techniques.
- Involves factorization and simplification of square roots manually.
- Can be time-consuming, especially for larger numbers.
- Offers deeper understanding and retention of mathematical principles.
- Using a Calculator:
- Quick and efficient, providing instant results.
- Reduces chances of manual errors.
- Useful for verifying manual calculations.
- Best for complex or large numbers where manual simplification is impractical.
Ultimately, the choice between manual calculation and using a calculator depends on the context and the user's comfort with mathematical procedures.
Examples of Simplifying Square Roots
Simplifying square roots involves reducing the expression under the square root sign to its simplest form. This process can often make calculations easier and more manageable. Here are some step-by-step examples to illustrate how to simplify square roots effectively:
- Example: Simplify \( \sqrt{12} \)
- Identify the factors of 12 that are perfect squares: \( 12 = 4 \times 3 \).
- Apply the rule \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \): \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} \).
- Simplify the square root of the perfect square: \( \sqrt{4} = 2 \).
- Combine the results: \( 2 \sqrt{3} \).
- So, \( \sqrt{12} \) simplifies to \( 2 \sqrt{3} \).
- Example: Simplify \( \sqrt{45} \)
- Identify the factors of 45 that are perfect squares: \( 45 = 9 \times 5 \).
- Apply the rule \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \): \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} \).
- Simplify the square root of the perfect square: \( \sqrt{9} = 3 \).
- Combine the results: \( 3 \sqrt{5} \).
- So, \( \sqrt{45} \) simplifies to \( 3 \sqrt{5} \).
- Example: Simplify \( \sqrt{72} \)
- Identify the factors of 72 that are perfect squares: \( 72 = 36 \times 2 \).
- Apply the rule \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \): \( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} \).
- Simplify the square root of the perfect square: \( \sqrt{36} = 6 \).
- Combine the results: \( 6 \sqrt{2} \).
- So, \( \sqrt{72} \) simplifies to \( 6 \sqrt{2} \).
- Example: Simplify \( \sqrt{50} \)
- Identify the factors of 50 that are perfect squares: \( 50 = 25 \times 2 \).
- Apply the rule \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \): \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} \).
- Simplify the square root of the perfect square: \( \sqrt{25} = 5 \).
- Combine the results: \( 5 \sqrt{2} \).
- So, \( \sqrt{50} \) simplifies to \( 5 \sqrt{2} \).
By following these steps and practicing with different numbers, you can master the process of simplifying square roots and make complex calculations much simpler.
Common Mistakes and How to Avoid Them
When simplifying square roots, it’s essential to avoid common mistakes that can lead to incorrect results. Here are some frequent errors and how to avoid them:
-
Not Recognizing Perfect Squares:
Always check if the number under the square root is a perfect square. If it is, simplify it directly. For example, \(\sqrt{25} = 5\).
-
Forgetting to Simplify Completely:
Ensure that you simplify the square root as much as possible. For instance, \(\sqrt{72}\) can be broken down to \(\sqrt{36 \times 2} = 6\sqrt{2}\).
-
Incorrectly Splitting the Radicand:
When simplifying, split the radicand correctly into factors, with one being a perfect square. For example, for \(\sqrt{50}\), use \(\sqrt{25 \times 2} = 5\sqrt{2}\).
-
Ignoring Negative Radicands:
Remember that the square root of a negative number is not a real number. Use imaginary numbers for these cases, such as \(\sqrt{-1} = i\).
-
Mistakes with Fractional Radicands:
When dealing with fractions under a square root, simplify the numerator and the denominator separately. For example, \(\sqrt{\frac{16}{25}} = \frac{4}{5}\).
By keeping these points in mind and practicing regularly, you can avoid common mistakes and simplify square roots accurately.
Advanced Techniques in Simplifying Radicals
Mastering the simplification of radicals can enhance your mathematical skills. Here are some advanced techniques to consider:
-
Prime Factorization:
Break down the number inside the radical into its prime factors. For example, to simplify \( \sqrt{72} \), factor it as \( 2^3 \times 3^2 \).
-
Pairing Factors:
Identify pairs of the same factor. Each pair can be moved outside the square root. For \( \sqrt{72} \), since \( 2^3 \) and \( 3^2 \) include pairs, it simplifies to \( 2^1 \times 3^1 \times \sqrt{2} = 6\sqrt{2} \).
-
Using Properties:
Apply properties like \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). This helps in splitting or combining radicals.
-
Rationalizing the Denominator:
To simplify expressions with radicals in the denominator, multiply the numerator and denominator by the conjugate or an appropriate radical. For example, \( \frac{1}{\sqrt{2}} \) can be rationalized to \( \frac{\sqrt{2}}{2} \).
-
Combining Like Terms:
Combine radicals with the same radicand. For instance, \( 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5} \).
These techniques not only simplify calculations but also make expressions easier to understand and use in further mathematical applications.

Applications of Simplified Square Roots
Simplified square roots have various applications across different fields. Understanding these can enhance both practical problem-solving skills and theoretical knowledge.
- Mathematics: Simplified square roots are essential in solving equations, especially in algebra and calculus, where they help in simplifying expressions for easier manipulation.
- Physics: In physics, they are used in formulas to calculate forces, energy, and other physical properties, making calculations more straightforward and results more interpretable.
- Engineering: Engineers use simplified radicals in designing structures and systems, where precise calculations are necessary for safety and efficiency.
- Finance: Square roots appear in financial models and calculations, such as in the standard deviation in statistics, which measures market volatility.
- Computer Science: Algorithms involving graphics and data processing often rely on simplified square roots to optimize performance.
By simplifying square roots, computations become less complex, allowing for more efficient problem-solving and clearer results.
Frequently Asked Questions
-
What is the square root of a number?
The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). For example, the square root of 16 is 4, because \( 4 \times 4 = 16 \).
-
How do I simplify square roots?
To simplify a square root, factor the number into its prime factors and pair them. For instance, to simplify \( \sqrt{18} \), factor 18 into \( 2 \times 3^2 \). Then, \( \sqrt{18} = 3\sqrt{2} \).
-
Can all square roots be simplified?
Not all square roots can be simplified into integers or simple radicals. Some square roots, like \( \sqrt{2} \), remain irrational and cannot be simplified further.
-
Why use a calculator for square roots?
A calculator provides quick and accurate results for both simple and complex square roots, ensuring precision in calculations that might be cumbersome manually.
-
What are some common mistakes when simplifying square roots?
Common mistakes include not completely factoring the number, forgetting to pair factors, or mistakenly simplifying irrational numbers.
-
How can I check my work when simplifying square roots?
Use a calculator to check your results or re-factor the number to ensure all steps are correct. Cross-checking with known values can also help verify accuracy.
Additional Resources and Tools
Here are some useful resources and tools for simplifying square roots:
- Omni Calculator: This tool simplifies radicals and provides step-by-step solutions, making it ideal for learning and practice.
- Mathway: Offers a comprehensive calculator that not only simplifies square roots but also shows exact and decimal forms for non-perfect squares.
- MathWarehouse: A straightforward calculator that reduces any square root to its simplest form and provides a rounded approximation.
- MathCracker: This calculator provides step-by-step calculations for simplifying radicals, using fundamental rules such as \(\sqrt{x} \cdot \sqrt{y} = \sqrt{xy}\).
These tools are excellent for anyone looking to deepen their understanding of square roots and radical simplification.
Khám phá cách sử dụng máy tính ClassWiz để đơn giản hóa căn bậc hai một cách hiệu quả trong đại số.
Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Hướng dẫn sử dụng máy tính đồ thị để đơn giản hóa căn bậc hai một cách chính xác và hiệu quả.
Đơn Giản Hóa Căn Bậc Hai Bằng Máy Tính Đồ Thị