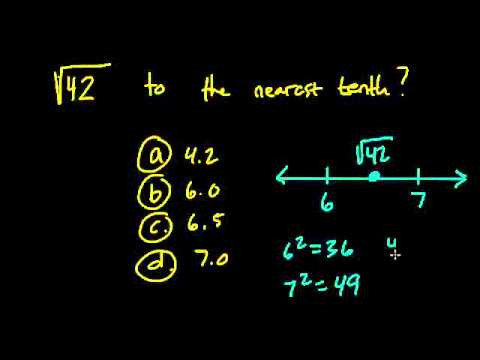Simplify Negative 5 Minus the Square Root of Negative 44

To simplify the expression \( -5 - \sqrt{-44} \), we need to follow a few steps. Here's a detailed guide:

Step-by-Step Solution

1. Identify the imaginary unit \(i\) where \( i = \sqrt{-1} \).

2. Rewrite the square root of the negative number using \(i\). For the given expression, we have:

   \[ \sqrt{-44} = \sqrt{44 \cdot -1} = \sqrt{44} \cdot \sqrt{-1} = \sqrt{44} \cdot i \]

3. Simplify \( \sqrt{44} \). We can factor 44 into \(4 \cdot 11\), and use the property \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \):

   \[ \sqrt{44} = \sqrt{4 \cdot 11} = \sqrt{4} \cdot \sqrt{11} = 2\sqrt{11} \]

4. Combine the results to get:

   \[ \sqrt{-44} = 2\sqrt{11}i \]

5. Substitute \( 2\sqrt{11}i \) back into the original expression:

   \[ -5 - \sqrt{-44} = -5 - 2\sqrt{11}i \]

The simplified form of the expression \( -5 - \sqrt{-44} \) is:

\[ -5 - 2\sqrt{11}i \]

When we encounter expressions involving the square root of negative numbers, we enter the realm of complex numbers, which are crucial in advanced mathematics. Simplifying an expression like $-5\; -\; \backslash sqrt\{-44\}$ involves breaking it down into real and imaginary parts.

To simplify this, we first address the square root of the negative number. The square root of $-44$ can be written as $\backslash sqrt\{44\}\; \backslash cdot\; \backslash sqrt\{-1\}$, recognizing that $\backslash sqrt\{-1\}\; =\; i$. Thus, $\backslash sqrt\{-44\}\; =\; \backslash sqrt\{44\}\; \backslash cdot\; i$.

Further simplifying $\backslash sqrt\{44\}$, we get $2\; \backslash sqrt\{11\}$. Combining these, we rewrite the expression as $-5\; -\; 2\; \backslash sqrt\{11\}i$.

This breakdown helps us understand how to handle complex numbers in mathematical expressions, setting the stage for deeper exploration into imaginary and complex number operations.

Imaginary numbers are a fundamental concept in mathematics that extend the number system to include solutions to equations involving the square root of negative numbers. The core idea is based on the imaginary unit, denoted as \(i\), where \(i = \sqrt{-1}\).

To understand imaginary numbers, let's explore their properties and applications:

• Definition: An imaginary number is defined as a multiple of the imaginary unit \(i\). For example, \(5i\) and \(-3i\) are imaginary numbers.
• Basic Operations: Just like real numbers, you can add, subtract, multiply, and divide imaginary numbers, following specific rules. For instance, \(i \times i = -1\).
• Complex Numbers: A complex number combines a real part and an imaginary part in the form \(a + bi\), where \(a\) and \(b\) are real numbers. For example, \(3 + 4i\) is a complex number.

Imaginary numbers are particularly useful in various fields of science and engineering. They allow us to solve equations that do not have real solutions and provide a way to describe phenomena such as electrical currents and waves.

Let’s delve into how these numbers are used in different contexts:

1. Solving Equations: Imaginary numbers enable solutions to equations like \(x^2 + 1 = 0\), which has no real solution. The solution in terms of imaginary numbers is \(x = \pm i\).
2. Polar Form and Exponential Representation: Complex numbers can be represented in polar form as \(r(\cos \theta + i \sin \theta)\), where \(r\) is the magnitude and \(\theta\) is the angle. This can also be expressed using Euler's formula as \(re^{i\theta}\).
3. Applications in Engineering: Imaginary numbers are crucial in analyzing electrical circuits and signals, where alternating current and waveforms are described using complex numbers.

Understanding and working with imaginary numbers expands our ability to solve problems across various disciplines, making them an essential part of modern mathematics.

To simplify the expression \(-5 - \sqrt{-44}\), follow these steps:

1. Identify the Imaginary Unit: Recognize that \(\sqrt{-44}\) involves an imaginary number. We can rewrite this as \(\sqrt{44} \cdot \sqrt{-1}\), where \(\sqrt{-1} = i\).
2. Simplify the Radical: Simplify \(\sqrt{44}\). Since \(44 = 4 \times 11\), we get \(\sqrt{44} = \sqrt{4 \times 11} = \sqrt{4} \times \sqrt{11} = 2\sqrt{11}\).
3. Combine the Terms: Substitute the simplified form into the expression:
   • \(-5 - \sqrt{-44} = -5 - (2\sqrt{11} \cdot i)\)
4. Final Form: The simplified form of the expression is \(-5 - 2i\sqrt{11}\).

By following these steps, you can simplify the expression involving imaginary numbers efficiently.

When dealing with the square root of a negative number, we enter the realm of imaginary numbers. These are essential in mathematics, especially in fields that require solving equations involving negative radicands. The key concept here is the imaginary unit \(i\), defined as \(i = \sqrt{-1}\).

To simplify the square root of a negative number, follow these steps:

1. Identify the negative number under the square root.
2. Express the negative number as the product of a positive number and \(-1\). For example, \(-44\) can be written as \(44 \times (-1)\).
3. Separate the square root into two parts: the square root of the positive number and the square root of \(-1\). Using our example, \(\sqrt{-44} = \sqrt{44} \times \sqrt{-1}\).
4. Replace \(\sqrt{-1}\) with \(i\), resulting in the expression \(\sqrt{44} \times i\).
5. Simplify the square root of the positive number if possible. For \(\sqrt{44}\), this simplifies to \(2\sqrt{11}\), as \(44\) is \(4 \times 11\), and the square root of \(4\) is \(2\).
6. Combine the results to get the simplified form. In our example, this gives us \(2\sqrt{11}i\).

Thus, the square root of a negative number like \(-44\) simplifies to \(2\sqrt{11}i\).

Understanding this breakdown is crucial for working with complex numbers and solving advanced mathematical problems that involve negative square roots.

When simplifying the expression \(-5 - \sqrt{-44}\), we first address the imaginary component. The square root of a negative number involves the imaginary unit \(i\), where \(i = \sqrt{-1}\).

Here are the steps to simplify:

1. Rewrite the square root of the negative number: \[ \sqrt{-44} = \sqrt{44} \cdot \sqrt{-1} = \sqrt{44} \cdot i \]
2. Simplify the square root of 44: \[ \sqrt{44} = \sqrt{4 \cdot 11} = 2\sqrt{11} \]
3. Combine the results: \[ \sqrt{-44} = 2\sqrt{11}i \]

Now, substitute back into the original expression:

\[
-5 - \sqrt{-44} = -5 - 2\sqrt{11}i
\]

Thus, the expression \(-5 - \sqrt{-44}\) is simplified to \(-5 - 2\sqrt{11}i\), combining the real part \(-5\) with the imaginary part \(-2\sqrt{11}i\).

To further understand the simplification of \(-5 - \sqrt{-44}\), let's go through some example problems.

Example 1:

Simplify the expression \(-3 - \sqrt{-25}\).

1. Rewrite the square root of the negative number: \[ \sqrt{-25} = \sqrt{25} \cdot \sqrt{-1} = 5i \]
2. Combine the results: \[ -3 - \sqrt{-25} = -3 - 5i \]

Example 2:

Simplify the expression \(2 - \sqrt{-9}\).

1. Rewrite the square root of the negative number: \[ \sqrt{-9} = \sqrt{9} \cdot \sqrt{-1} = 3i \]
2. Combine the results: \[ 2 - \sqrt{-9} = 2 - 3i \]

Example 3:

Simplify the expression \(-7 + \sqrt{-16}\).

1. Rewrite the square root of the negative number: \[ \sqrt{-16} = \sqrt{16} \cdot \sqrt{-1} = 4i \]
2. Combine the results: \[ -7 + \sqrt{-16} = -7 + 4i \]

By following these steps, you can simplify any expression involving the square root of a negative number and combine the real and imaginary parts.

When simplifying expressions involving imaginary numbers, such as -5 - \sqrt{-44}, there are several common mistakes that students often make. Here are some of the most frequent errors and tips on how to avoid them:

• Incorrect Simplification of Square Roots:

  One common mistake is failing to correctly simplify the square root of a negative number. For example, \(\sqrt{-44}\) should be simplified by recognizing that \(\sqrt{-44} = \sqrt{44} \cdot i\), where \(i\) is the imaginary unit (\(i^2 = -1\)). To avoid this mistake, always express the square root of a negative number in terms of \(i\).

  Correct simplification: \(\sqrt{-44} = \sqrt{44} \cdot i = \sqrt{4 \cdot 11} \cdot i = 2\sqrt{11} \cdot i\).

• Forgetting to Combine Like Terms:

  Another common error is forgetting to combine real and imaginary parts properly. For instance, in the expression -5 - 2\sqrt{11}i, ensure that you keep real and imaginary parts separate.

  Correct approach: Identify and separately combine the real part (\(-5\)) and the imaginary part (\(-2\sqrt{11}i\)).

• Sign Errors:

  Students often make sign errors when dealing with imaginary numbers, especially when multiplying or dividing by \(i\). Remember that \(i^2 = -1\).

  Tip: Carefully track the signs when performing arithmetic operations involving \(i\).

• Misunderstanding the Properties of Imaginary Numbers:

  It's crucial to understand that \(i\) behaves differently from real numbers. For example, \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) holds true for positive \(a\) and \(b\), but for negative values, you need to be careful.

  Correct understanding: Recognize when to apply the properties of square roots and when they don't directly apply to negative numbers under the radical.

By being mindful of these common mistakes and practicing careful arithmetic, you can effectively simplify complex expressions involving imaginary numbers.

Here are some practice questions to help you master the simplification of expressions involving imaginary numbers:

1. Simplify the expression \( -5 - \sqrt{-44} \).
   1. Extract the imaginary unit \( i \) from the square root:

      \( \sqrt{-44} = \sqrt{-1 \cdot 44} = \sqrt{-1} \cdot \sqrt{44} = i \cdot \sqrt{44} \).

   2. Rewrite the expression:

      \( -5 - \sqrt{-44} = -5 - i \cdot \sqrt{44} \).

   3. Simplify the square root (if possible):

      \( \sqrt{44} = \sqrt{4 \cdot 11} = 2 \sqrt{11} \).

   4. Combine all parts:

      \( -5 - i \cdot 2\sqrt{11} = -5 - 2i\sqrt{11} \).

2. Simplify \( \sqrt{-16} \).
   1. Extract the imaginary unit:

      \( \sqrt{-16} = \sqrt{-1 \cdot 16} = \sqrt{-1} \cdot \sqrt{16} = i \cdot 4 = 4i \).

3. Simplify \( \sqrt{-9} - 2 \).
   1. Extract the imaginary unit:

      \( \sqrt{-9} = \sqrt{-1 \cdot 9} = \sqrt{-1} \cdot \sqrt{9} = i \cdot 3 = 3i \).

   2. Combine with the constant:

      \( 3i - 2 \).

4. Simplify \( \sqrt{-50} \).
   1. Extract the imaginary unit:

      \( \sqrt{-50} = \sqrt{-1 \cdot 50} = \sqrt{-1} \cdot \sqrt{50} = i \cdot \sqrt{50} \).

   2. Simplify the square root:

      \( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \).

   3. Combine all parts:

      \( i \cdot 5\sqrt{2} = 5i\sqrt{2} \).

5. Simplify \( -3 + \sqrt{-36} \).
   1. Extract the imaginary unit:

      \( \sqrt{-36} = \sqrt{-1 \cdot 36} = \sqrt{-1} \cdot \sqrt{36} = i \cdot 6 = 6i \).

   2. Combine with the constant:

      \( -3 + 6i \).

In this tutorial, we have explored the steps to simplify the expression \( -5 - \sqrt{-44} \). We broke down the complex number into its real and imaginary parts and combined them effectively.

By rewriting the square root of a negative number using the imaginary unit \( i \), we transformed \( \sqrt{-44} \) into \( 2i\sqrt{11} \). This allowed us to express the original expression as \( -5 - 2i\sqrt{11} \).

The key steps involved were:

• Identifying the square root of the negative number: \( \sqrt{-44} = \sqrt{44} \cdot \sqrt{-1} \).
• Simplifying the square root of the positive number: \( \sqrt{44} = 2\sqrt{11} \).
• Incorporating the imaginary unit: \( \sqrt{-44} = 2i\sqrt{11} \).
• Combining the results to get the final expression: \( -5 - 2i\sqrt{11} \).

Understanding how to simplify expressions involving imaginary numbers is crucial for working with complex numbers. This process demonstrates the importance of breaking down problems into smaller, manageable steps and systematically applying mathematical rules.

By practicing these steps, you can confidently handle similar problems involving complex numbers and their simplification.

To deepen your understanding of simplifying expressions involving square roots of negative numbers and combining real and imaginary parts, explore the following resources:

• Simplifying the Square Root of a Negative Number: This tutorial provides a detailed explanation on how to simplify the square root of negative numbers using the imaginary unit \(i\). Visit the for more information.

• Khan Academy Video Lessons: Watch instructional videos that cover the fundamentals of imaginary and complex numbers, including step-by-step examples. Check out the for visual learning.

• Symbolab Simplify Calculator: Use this online tool to practice simplifying complex expressions. It provides step-by-step solutions and explanations. Try it out on .

• Further Exploration in Algebra: Explore additional algebraic concepts such as solving quadratic equations with imaginary solutions and prime factorization. Visit the for comprehensive tutorials.

By utilizing these resources, you'll gain a stronger grasp of the mathematical principles and techniques needed to simplify expressions involving complex numbers.