Topic simplify square root with variables calculator: Discover how to effortlessly simplify square roots with variables using our comprehensive calculator. This guide will walk you through step-by-step processes, practical examples, and expert tips to make simplifying square roots with variables a breeze. Whether you're a student or a math enthusiast, this resource is designed to enhance your understanding and skills.
Table of Content
- How to Simplify Square Roots with Variables
- Introduction to Simplifying Square Roots with Variables
- Understanding Square Roots
- Simplifying Square Roots of Single Variables
- Simplifying Square Roots of Multiple Variables
- Simplifying Square Roots of Products
- Simplifying Square Roots of Fractions
- Square Root Calculators and Tools
- Practical Applications of Simplifying Square Roots
- YOUTUBE: Hướng dẫn chi tiết về cách đơn giản hóa căn bậc hai với biến trong toán học, giúp người xem nắm bắt dễ dàng và chính xác.
How to Simplify Square Roots with Variables
Simplifying square roots with variables involves breaking down the expression under the radical into its prime factors and applying the properties of square roots.
Using a Calculator
Online calculators like Symbolab and Omni Calculator can help simplify square roots with variables by following step-by-step solutions. These calculators allow input of expressions and provide detailed explanations on how to simplify them.
Basic Steps for Simplification
- Factor the expression under the square root into prime factors.
- Group the factors into pairs.
- Move each pair out of the radical as a single number or variable.
- Simplify the remaining expression under the radical.
Example
Consider the expression \( \sqrt{12x^2} \):
- Factor inside the radical: \( \sqrt{4 \cdot 3 \cdot x^2} \)
- Take the square root of each pair: \( 2x\sqrt{3} \)
Using Online Tools
Online calculators like CalculatorSoup and dCode offer tools that simplify radicals with variables and provide detailed work solutions, making them useful for both learning and quick calculations.

READ MORE:
Introduction to Simplifying Square Roots with Variables
Understanding how to simplify square roots that include variables is essential for solving various algebraic expressions. Simplifying these roots involves breaking down the expression under the radical into its prime factors, and then applying the properties of square roots to simplify the expression as much as possible. This process can make complex algebraic equations easier to handle and solve.
Here are the steps to simplify square roots with variables:
-
Identify Perfect Squares:
First, identify and separate the perfect square factors from the non-perfect square factors in the expression.
-
Break Down the Expression:
Rewrite the expression by factoring out the perfect squares. For example, \( \sqrt{64x^8} \) can be factored as \( \sqrt{(8x^4)^2} \).
-
Apply the Square Root:
Apply the square root to the perfect square factor. In the previous example, \( \sqrt{(8x^4)^2} \) simplifies to \( 8x^4 \).
-
Simplify Remaining Factors:
Combine and simplify any remaining factors under the square root that cannot be factored into perfect squares.
Let’s look at some examples to illustrate these steps:
| \(\sqrt{64x^8}\) | \(= \sqrt{(8x^4)^2}\) | \(= 8x^4\) |
| \(\sqrt{225x^4}\) | \(= \sqrt{(15x^2)^2}\) | \(= 15x^2\) |
| \(\sqrt{784x^2}\) | \(= \sqrt{(28x)^2}\) | \(= 28x\) |
These steps and examples demonstrate the basic method for simplifying square roots with variables. By consistently applying these techniques, you can simplify a wide range of algebraic expressions involving square roots and variables.
Understanding Square Roots
Square roots are fundamental in mathematics, particularly when dealing with variables. A square root of a number or expression is a value that, when multiplied by itself, gives the original number or expression. Simplifying square roots with variables involves breaking down the expression under the square root into its prime factors, allowing for easier manipulation and simplification.
Here are the key concepts to understand when simplifying square roots with variables:
- Prime Factorization: Break down the number and the variables inside the square root into their prime factors.
- Pairing Factors: For every pair of identical factors, one factor can be taken out of the square root.
- Simplifying Variables: When variables are involved, ensure that exponents are handled correctly by taking half of the exponent for each variable outside the square root.
Let's look at some examples to illustrate these steps:
- Example 1: \(\sqrt{64x^8}\)
- Example 2: \(\sqrt{225x^4}\)
- Example 3: \(\sqrt{784x^2}\)
\[
\sqrt{64x^8} = \sqrt{(2^6)(x^8)} = \sqrt{2^6} \cdot \sqrt{x^8} = 2^3 \cdot x^4 = 8x^4
\]
\[
\sqrt{225x^4} = \sqrt{(15^2)(x^4)} = 15 \cdot \sqrt{x^4} = 15x^2
\]
\[
\sqrt{784x^2} = \sqrt{(28^2)(x^2)} = 28 \cdot \sqrt{x^2} = 28x
\]
By understanding these principles, you can simplify even the most complex square root expressions with variables. Practice with different expressions to gain confidence and master the technique of simplifying square roots with variables.
Simplifying Square Roots of Single Variables
When simplifying the square root of a variable, it's important to understand how to manipulate the exponents correctly. Here’s a detailed, step-by-step guide:
- Identify the variable inside the square root. For example, consider \(\sqrt{x^8}\).
- Rewrite the exponent in terms of squares: \(x^8 = (x^4)^2\).
- Apply the square root to both the coefficient and the variable: \(\sqrt{(x^4)^2} = x^4\).
- The simplified form of \(\sqrt{x^8}\) is \(x^4\).
Let's go through a few more examples:
- \(\sqrt{x^2} = x\)
- \(\sqrt{x^4} = x^2\)
- \(\sqrt{x^6} = x^3\)
In general, \(\sqrt{x^{2n}} = x^n\). This method works because you are essentially "halving" the exponent when you take the square root.
Here are some practice problems:
- Simplify \(\sqrt{x^{10}}\).
- Simplify \(\sqrt{x^{14}}\).
- Simplify \(\sqrt{x^{20}}\).
Remember, the key is to express the variable's exponent as a multiple of 2, then simplify accordingly. Happy simplifying!
Simplifying Square Roots of Multiple Variables
When simplifying square roots involving multiple variables, the process involves breaking down each variable separately and then combining the results. This ensures the expression is in its simplest form. Here's a detailed guide to help you through the process:
- Identify and separate the variables inside the square root.
- Apply the square root to each variable independently.
- Simplify each square root by breaking down the exponents.
Let's consider the example of simplifying \(\sqrt{a^4b^2}\):
- Break down the expression: \(\sqrt{a^4b^2} = \sqrt{a^4} \cdot \sqrt{b^2}\).
- Simplify each term: \(\sqrt{a^4} = a^2\) and \(\sqrt{b^2} = b\).
- Combine the results: \(a^2 \cdot b\).
Therefore, \(\sqrt{a^4b^2} = a^2b\).
Here’s another example with different exponents: \(\sqrt{c^6d^8}\):
- Separate the variables: \(\sqrt{c^6d^8} = \sqrt{c^6} \cdot \sqrt{d^8}\).
- Simplify each square root:
- \(\sqrt{c^6} = c^3\), because \(6/2 = 3\).
- \(\sqrt{d^8} = d^4\), because \(8/2 = 4\).
- Combine the simplified terms: \(c^3d^4\).
So, \(\sqrt{c^6d^8} = c^3d^4\).
By following these steps, you can simplify any square root involving multiple variables. Always remember to deal with each variable separately and apply the square root properties accurately for the best results.
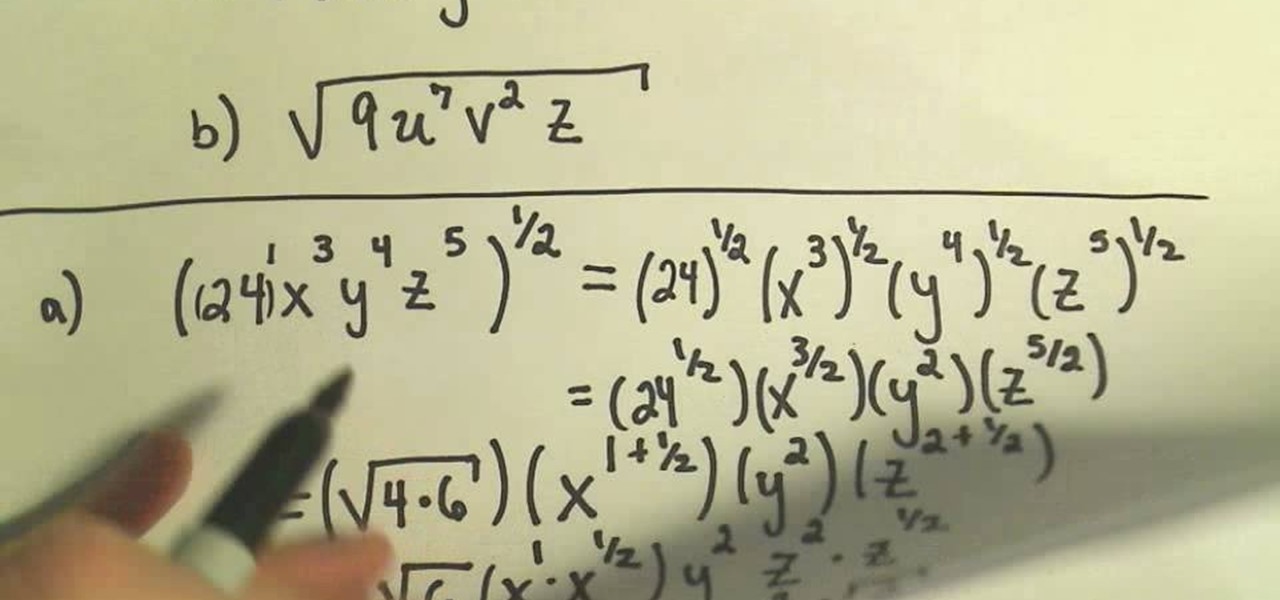
Simplifying Square Roots of Products
When simplifying square roots that involve the product of multiple variables and numbers, we can use the property of square roots that allows us to break down the product into separate square roots. This can make the process simpler and more straightforward. The steps are as follows:
-
Identify the product under the square root. For example, consider the expression \( \sqrt{a \cdot b} \).
-
Apply the property of square roots that \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \).
-
Simplify each square root individually if possible.
- For instance, if \( a = 9 \) and \( b = 16 \), then \( \sqrt{9 \cdot 16} = \sqrt{9} \cdot \sqrt{16} \).
- This simplifies to \( 3 \cdot 4 \) because \( \sqrt{9} = 3 \) and \( \sqrt{16} = 4 \).
- Thus, \( \sqrt{9 \cdot 16} = 12 \).
-
Combine the simplified square roots to get the final result.
Let's consider another example involving variables: \( \sqrt{x^2 \cdot y^4} \).
-
Apply the property: \( \sqrt{x^2 \cdot y^4} = \sqrt{x^2} \cdot \sqrt{y^4} \).
-
Simplify each square root:
- \( \sqrt{x^2} = x \).
- \( \sqrt{y^4} = y^2 \).
-
Combine the results: \( x \cdot y^2 \).
By following these steps, we can simplify square roots of products in a systematic and straightforward manner.
Simplifying Square Roots of Fractions
Simplifying square roots of fractions involves several steps to ensure the fraction is in its simplest form. The process includes rationalizing the denominator and handling complex fractions. Let's explore these steps in detail.
Rationalizing the Denominator
Rationalizing the denominator means converting the denominator of a fraction into a rational number (i.e., a number without a square root). This is done by multiplying both the numerator and the denominator by an appropriate value.
- Identify the radical in the denominator. For example, consider the fraction \( \frac{1}{\sqrt{a}} \).
- Multiply the numerator and the denominator by the radical in the denominator: \( \frac{1 \cdot \sqrt{a}}{\sqrt{a} \cdot \sqrt{a}} = \frac{\sqrt{a}}{a} \).
- Simplify the expression: \( \frac{\sqrt{a}}{a} \).
In this way, the denominator is rationalized.
Complex Fraction Examples
For more complex fractions, the process might involve additional steps, such as combining like terms or dealing with higher powers. Let's look at some examples.
Example 1: Simplify \( \frac{\sqrt{2}}{\sqrt{3}} \).
- Multiply the numerator and the denominator by \( \sqrt{3} \): \( \frac{\sqrt{2} \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{\sqrt{6}}{3} \).
- Simplify the expression: \( \frac{\sqrt{6}}{3} \).
Example 2: Simplify \( \frac{\sqrt{x}}{\sqrt{y}} \).
- Multiply the numerator and the denominator by \( \sqrt{y} \): \( \frac{\sqrt{x} \cdot \sqrt{y}}{\sqrt{y} \cdot \sqrt{y}} = \frac{\sqrt{xy}}{y} \).
- Simplify the expression: \( \frac{\sqrt{xy}}{y} \).
Example 3: Simplify \( \frac{\sqrt{x^2 + 1}}{\sqrt{x - 1}} \).
- Multiply the numerator and the denominator by \( \sqrt{x - 1} \): \( \frac{\sqrt{x^2 + 1} \cdot \sqrt{x - 1}}{\sqrt{x - 1} \cdot \sqrt{x - 1}} = \frac{\sqrt{(x^2 + 1)(x - 1)}}{x - 1} \).
- Expand and simplify the numerator: \( \frac{\sqrt{x^3 - x^2 + x - 1}}{x - 1} \).
These examples illustrate the steps involved in simplifying square roots of fractions. By following these steps, you can ensure your expressions are in their simplest form, making them easier to work with in further calculations.
Square Root Calculators and Tools
Using a square root calculator can greatly simplify the process of finding and simplifying square roots, especially when variables are involved. Here are some useful tools and guidelines on how to use them:
How to Use a Square Root Calculator
- Enter the number or expression for which you need to calculate the square root.
- Click on the 'Calculate' button to find the square root. The calculator will provide step-by-step solutions.
- If you need to calculate another expression, click on the 'Reset' button and enter new values.
These calculators can handle both numerical and variable expressions, providing simplified results quickly and accurately.
Popular Online Calculators
- Symbolab Simplify Calculator: This tool offers a wide range of functions including simplification of square roots, factoring, and algebraic operations. It provides detailed steps for each calculation.
- MathCracker Square Root Calculator: This calculator not only computes the square root but also simplifies the expressions step-by-step, following basic rules such as \(\sqrt{x \cdot y} = \sqrt{x} \cdot \sqrt{y}\) and \(\frac{\sqrt{x}}{\sqrt{y}} = \sqrt{\frac{x}{y}}\).
- Cuemath Square Root Calculator: Cuemath's tool is user-friendly and provides clear steps for simplifying expressions with variables. For example, to simplify \(\sqrt{64x^8}\), it breaks down the factors and groups them to find \(8x^4\).
Benefits of Using Square Root Calculators
These calculators are beneficial for several reasons:
- Accuracy: They ensure precise calculations, reducing the risk of errors.
- Step-by-Step Solutions: They provide detailed steps, which is helpful for learning and verification.
- Time-Saving: They quickly handle complex calculations, saving time and effort.
Using these tools can enhance your understanding of simplifying square roots and improve your efficiency in solving mathematical problems involving radicals.
Practical Applications of Simplifying Square Roots
Simplifying square roots is not just a theoretical exercise; it has numerous practical applications in various fields. Here are some key areas where simplified square roots are commonly used:
Algebraic Equations
In algebra, simplifying square roots is essential for solving equations. For example, consider the quadratic equation:
\[
ax^2 + bx + c = 0
\]
The solution involves the quadratic formula:
\[
x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a}
\]
Simplifying the expression under the square root, known as the discriminant, helps in finding the roots of the equation more easily.
Geometric Problems
In geometry, square roots are often encountered when dealing with distances and areas. For instance:
- Distance Formula: The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a coordinate plane is given by: \[ d = \sqrt{{(x_2 - x_1)^2 + (y_2 - y_1)^2}} \] Simplifying this square root helps in calculating the exact distance.
- Area of a Triangle: Using Heron's formula, the area of a triangle with sides \(a\), \(b\), and \(c\) is: \[ A = \sqrt{{s(s-a)(s-b)(s-c)}} \] where \(s\) is the semi-perimeter \(\left(\frac{{a+b+c}}{2}\right)\). Simplifying the square root expression makes it easier to find the area.
Physics and Engineering
In physics and engineering, square roots appear in various formulas and calculations. For example:
- Wave Speed: The speed of a wave on a string is given by: \[ v = \sqrt{{\frac{T}{\mu}}} \] where \(T\) is the tension and \(\mu\) is the linear mass density. Simplifying this expression is crucial for accurate measurements.
- Ohm's Law: In electrical engineering, the relationship between voltage (\(V\)), current (\(I\)), and resistance (\(R\)) can involve square roots when dealing with power calculations.
Statistics
In statistics, square roots are often used in the calculation of standard deviation and variance, which are measures of data dispersion. For example, the standard deviation (\(\sigma\)) is given by:
\[
\sigma = \sqrt{{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}}
\]
Simplifying the square root expression helps in understanding the spread of the data.
Understanding how to simplify square roots is essential for these applications, making complex calculations more manageable and accurate.

Hướng dẫn chi tiết về cách đơn giản hóa căn bậc hai với biến trong toán học, giúp người xem nắm bắt dễ dàng và chính xác.
Căn Bậc Hai Với Biến (Đơn Giản Hóa Toán Học)
READ MORE:
Hướng dẫn sử dụng máy tính ClassWiz để đơn giản hóa biểu thức căn bậc hai, bài học Đại Số 4-1 giúp bạn dễ dàng hiểu và thực hành.
Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hóa Biểu Thức Căn Bậc Hai