Topic simplify square root of 49: Learning to simplify the square root of 49 is fundamental in mathematics. This article provides a comprehensive guide on various methods to simplify square roots, along with practical examples and exercises. By understanding these techniques, you'll be equipped to tackle similar problems with ease and avoid common mistakes. Explore the applications of simplifying square roots and enhance your problem-solving skills.
Table of Content
- How to Simplify the Square Root of 49
- Introduction
- Understanding the Concept of Square Roots
- Methods to Simplify Square Roots
- Example Problems
- Practice Exercises
- Common Mistakes and How to Avoid Them
- Applications of Simplifying Square Roots
- Conclusion
- YOUTUBE: Video giới thiệu về cách đơn giản hóa căn bậc hai của 49, hướng dẫn chi tiết và dễ hiểu, phù hợp cho học sinh và người mới bắt đầu.
How to Simplify the Square Root of 49
To simplify the square root of 49, you can follow these steps:
- Recognize that \( \sqrt{49} \) represents the number which, when multiplied by itself, equals 49.
- Since \( 49 = 7 \times 7 \), we have \( \sqrt{49} = \sqrt{7 \times 7} \).
- Using the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \), simplify to \( \sqrt{49} = \sqrt{7} \times \sqrt{7} = 7 \).
Therefore, the simplified form of \( \sqrt{49} \) is \( 7 \).

READ MORE:
Introduction
Simplifying the square root of 49 involves finding a number which, when multiplied by itself, equals 49. In this case, the square root of 49 is 7, as 7 × 7 = 49. This concept is foundational in mathematics, extending to more complex equations and applications in fields such as physics and engineering. Understanding how to simplify square roots is crucial for solving various mathematical problems efficiently.
Understanding the Concept of Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 49 is 7 because 7 multiplied by 7 equals 49.
Mathematically, the square root is represented by the radical symbol (√). So, the square root of 49 is written as √49.
Prime Factorization Method
One way to understand square roots is through prime factorization. Here’s how you can simplify the square root of 49 using this method:
Express the number as a product of its prime factors:
\[ 49 = 7 \times 7 \]
Since we have a pair of the same number (7), we take one number from the pair:
\[ \sqrt{49} = 7 \]
Properties of Square Roots
There are several properties of square roots that are useful in simplifying them:
Square root of a product:
\[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \]
Square root of a quotient:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
Power of a square root:
\[ \sqrt{a^2} = a \]
Examples of Simplifying Square Roots
Let's look at a few more examples to solidify our understanding:
Simplifying √36:
\[ 36 = 6 \times 6 \]
\[ \sqrt{36} = 6 \]
Simplifying √81:
\[ 81 = 9 \times 9 \]
\[ \sqrt{81} = 9 \]
Simplifying √64:
\[ 64 = 8 \times 8 \]
\[ \sqrt{64} = 8 \]
In conclusion, understanding the concept of square roots involves recognizing them as values that, when squared, return the original number. Using methods like prime factorization and recognizing properties of square roots can greatly simplify the process of finding square roots of various numbers.
Methods to Simplify Square Roots
Simplifying square roots involves expressing the root in its simplest form. Below are several methods and steps to achieve this:
Prime Factorization Method
This method involves breaking down the number inside the square root into its prime factors.
- Factor the number: Start by finding the prime factors of the number. For example, to simplify \(\sqrt{49}\):
- 49 can be factored as \(7 \times 7\)
- Group the factors: Pair the prime factors.
- \(\sqrt{49} = \sqrt{7 \times 7}\)
- Simplify the root: Take one number from each pair outside the square root.
- \(\sqrt{7 \times 7} = 7\)
Square Root Properties
Use the properties of square roots to simplify. One useful property is:
\(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- Decompose the number: For example, to simplify \(\sqrt{45}\):
- 45 can be expressed as \(9 \times 5\)
- Apply the property: Use the property to separate the factors.
- \(\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5}\)
- Simplify each square root: Simplify the perfect square root.
- \(\sqrt{9} = 3\), so \(\sqrt{45} = 3\sqrt{5}\)
Using the Perfect Square Method
Identify and utilize perfect squares within the number.
- Find the perfect square factors: For example, to simplify \(\sqrt{72}\):
- 72 can be expressed as \(36 \times 2\)
- Apply the square root property: Separate the perfect square.
- \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2}\)
- Simplify the perfect square: Simplify \(\sqrt{36}\).
- \(\sqrt{36} = 6\), so \(\sqrt{72} = 6\sqrt{2}\)
Combining and Simplifying Surds
Sometimes, it helps to combine and then simplify surds.
- Combine the surds: For example, \(\sqrt{6} \times \sqrt{15}\):
- \(\sqrt{6} \times \sqrt{15} = \sqrt{6 \times 15} = \sqrt{90}\)
- Factor the number: Factor 90 into primes.
- 90 = \(9 \times 10 = 3^2 \times 2 \times 5\)
- Simplify the square root: Simplify using the prime factors.
- \(\sqrt{90} = \sqrt{3^2 \times 2 \times 5} = 3\sqrt{10}\)
By using these methods, you can simplify any square root to its most basic form.
Example Problems
Understanding how to simplify square roots through example problems is crucial for mastering this mathematical concept. Here are detailed examples to guide you:
Example 1: Simplify \( \sqrt{49} \)
To simplify \( \sqrt{49} \), we need to find a number that, when multiplied by itself, equals 49. The number is 7, since \( 7 \times 7 = 49 \). Therefore:
\[
\sqrt{49} = 7
\]
Example 2: Simplify \( \sqrt{72} \)
We start by factoring 72 into its prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \). Group the prime factors into pairs:
\[
\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = \sqrt{4 \times 9 \times 2} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}
\]
Therefore, \( \sqrt{72} \) simplifies to \( 6\sqrt{2} \).
Example 3: Simplify \( \sqrt{18} \)
Factor 18 into its prime factors: \( 18 = 2 \times 3 \times 3 \). Group the prime factors into pairs:
\[
\sqrt{18} = \sqrt{2 \times (3 \times 3)} = \sqrt{2 \times 9} = \sqrt{2} \times \sqrt{9} = \sqrt{2} \times 3 = 3\sqrt{2}
\]
Thus, \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \).
Example 4: Simplify \( \sqrt{50} \)
Factor 50 into its prime factors: \( 50 = 2 \times 5 \times 5 \). Group the prime factors into pairs:
\[
\sqrt{50} = \sqrt{(5 \times 5) \times 2} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}
\]
Therefore, \( \sqrt{50} \) simplifies to \( 5\sqrt{2} \).
Example 5: Simplify \( 2\sqrt{12} + 3\sqrt{3} \)
First, simplify \( 2\sqrt{12} \). Factor 12 into its prime factors: \( 12 = 2 \times 2 \times 3 \):
\[
2\sqrt{12} = 2\sqrt{(2 \times 2) \times 3} = 2\sqrt{4 \times 3} = 2 \times 2\sqrt{3} = 4\sqrt{3}
\]
Now add \( 4\sqrt{3} \) and \( 3\sqrt{3} \):
\[
4\sqrt{3} + 3\sqrt{3} = (4 + 3)\sqrt{3} = 7\sqrt{3}
\]
Thus, \( 2\sqrt{12} + 3\sqrt{3} \) simplifies to \( 7\sqrt{3} \).
Example 6: Simplify \( 10\sqrt{49} + 7 \)
Given \( 10\sqrt{49} + 7 \), and knowing \( \sqrt{49} = 7 \):
\[
10\sqrt{49} + 7 = 10 \times 7 + 7 = 70 + 7 = 77
\]
Therefore, the expression simplifies to 77.
Example 7: Solve for \( p \) if \( p\sqrt{49} = 21 \)
We know \( \sqrt{49} = 7 \). Substitute and solve for \( p \):
\[
p \times 7 = 21 \implies p = \frac{21}{7} = 3
\]
Thus, the value of \( p \) is 3.
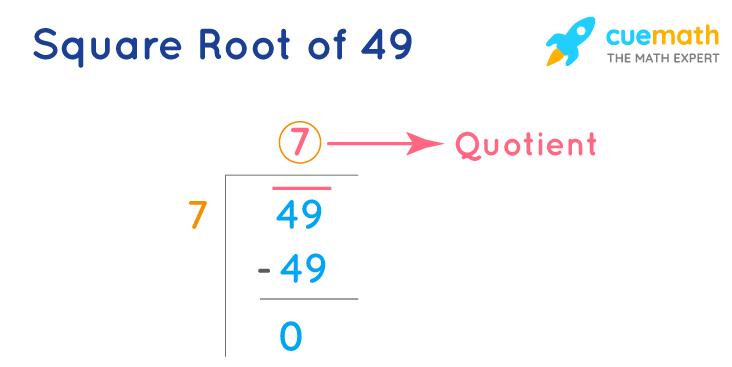
Practice Exercises
Practicing how to simplify square roots is crucial for mastering this mathematical concept. Below are several exercises designed to help you practice simplifying the square root of 49 and similar problems. Follow the steps provided and check your work.
-
Simplify
\(\sqrt{49}\):- Since \(49\) is a perfect square, identify its square root: \(49 = 7^2\).
- Therefore,
\(\sqrt{49} = 7\).
-
Simplify
\(\sqrt{36}\):- Recognize that \(36\) is a perfect square: \(36 = 6^2\).
- Thus,
\(\sqrt{36} = 6\).
-
Simplify
\(\sqrt{81}\):- Identify \(81\) as a perfect square: \(81 = 9^2\).
- Hence,
\(\sqrt{81} = 9\).
-
Simplify
\(\sqrt{100}\):- Notice that \(100\) is a perfect square: \(100 = 10^2\).
- Therefore,
\(\sqrt{100} = 10\).
-
Simplify
\(\sqrt{64}\):- Recognize \(64\) as a perfect square: \(64 = 8^2\).
- Thus,
\(\sqrt{64} = 8\).
-
Simplify
\(\sqrt{121}\):- Identify \(121\) as a perfect square: \(121 = 11^2\).
- Hence,
\(\sqrt{121} = 11\).
-
Simplify
\(\sqrt{144}\):- Notice that \(144\) is a perfect square: \(144 = 12^2\).
- Therefore,
\(\sqrt{144} = 12\).
Keep practicing with these exercises to solidify your understanding of simplifying square roots. You can also create similar problems by identifying other perfect squares.
Common Mistakes and How to Avoid Them
While simplifying square roots, it's easy to make mistakes. Here are some common errors and tips on how to avoid them:
- Forgetting to check for perfect squares: Always look for perfect square factors within the radicand (the number inside the square root). For example, in simplifying
√49, recognize that49is a perfect square (72), so√49 = 7. - Rushing through the process: Take your time to ensure each step is correct. Rushing can lead to errors in factorization or misapplication of the rules.
- Incorrectly applying the product rule: Remember that
√(a * b) = √a * √bonly whenaandbare non-negative. Misapplication can lead to incorrect simplifications. - Ignoring negative solutions: When solving equations involving square roots, don't forget to consider both positive and negative solutions. For instance, if
x2 = 49, thenx = ±7.
Here are steps to avoid these mistakes:
- Identify and extract perfect square factors from the radicand. For example, for
√72, recognize that72 = 36 * 2, and since36is a perfect square, you can simplify it to6√2. - Write out each step to avoid skipping parts of the process. For instance, to simplify
√50:- Factorize
50into25 * 2 - Apply the product rule:
√50 = √(25 * 2) = √25 * √2 - Simplify:
√25 = 5, so√50 = 5√2
- Factorize
- Practice regularly with different problems to become familiar with various types of simplifications.
- Double-check your solutions by substituting them back into the original equation to ensure they satisfy it.
By following these tips and practicing regularly, you can avoid common mistakes and become proficient in simplifying square roots.
Applications of Simplifying Square Roots
Simplifying square roots is a fundamental skill that finds application in various fields, from everyday life to advanced scientific research. Here are some common applications:
- Geometry: In geometry, simplifying square roots is crucial for calculating distances, areas, and volumes. For example, the Pythagorean theorem often requires simplifying the square root of the sum of squares of the sides of a right triangle to find the length of the hypotenuse.
- Engineering: Engineers often simplify square roots to solve problems related to design and analysis. For instance, in electrical engineering, the impedance of a circuit with resistance and reactance is determined using the square root of the sum of squares of these components.
- Physics: In physics, many formulas involve square roots. For example, the formula for the period of a pendulum includes the square root of the length of the pendulum divided by the acceleration due to gravity.
- Statistics: In statistics, standard deviation and variance calculations often require simplifying square roots. The standard deviation is the square root of the variance and is used to measure the dispersion of data points in a dataset.
- Everyday Life: Simplifying square roots can also be useful in daily activities. For example, determining the diagonal length of a television screen or a rectangular table involves simplifying the square root of the sum of the squares of its width and height.
Example Problems
Let's consider a few example problems to see how simplifying square roots can be applied:
- Geometry: Find the length of the hypotenuse of a right triangle with legs of 3 units and 4 units.
Using the Pythagorean theorem: \( c = \sqrt{a^2 + b^2} \)
\( c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) units. - Physics: Calculate the period of a pendulum with a length of 2 meters.
Using the formula \( T = 2\pi \sqrt{\frac{L}{g}} \), where \( L \) is the length and \( g \) is the acceleration due to gravity (approximately 9.8 m/s²):
\( T = 2\pi \sqrt{\frac{2}{9.8}} \approx 2\pi \sqrt{0.204} \approx 2\pi \times 0.451 \approx 2.83 \) seconds.
Understanding and applying the concept of simplifying square roots is essential in solving real-world problems efficiently and accurately.
Conclusion
Simplifying square roots, such as the square root of 49, is an essential skill in mathematics that has broad applications in various fields. The process of simplifying square roots involves breaking down the number under the radical sign into its prime factors and identifying perfect squares.
In the case of \( \sqrt{49} \), the number 49 is already a perfect square, since \( 7 \times 7 = 49 \). Thus, \( \sqrt{49} = 7 \). This simplicity highlights the importance of recognizing perfect squares and their roots, which can streamline calculations and problem-solving.
Throughout this guide, we have explored:
- The fundamental concepts of square roots and their properties.
- Various methods to simplify square roots, including prime factorization and recognizing perfect squares.
- Common mistakes to avoid, such as incorrectly identifying perfect squares or improper simplification techniques.
- Real-world applications, demonstrating the relevance of this mathematical process in practical scenarios.
Mastering the technique of simplifying square roots not only enhances mathematical understanding but also improves problem-solving skills across different domains. Remember to practice regularly, apply the methods correctly, and avoid common pitfalls. By doing so, you will gain confidence and proficiency in simplifying square roots and related mathematical tasks.
Thank you for following this guide on simplifying square roots. Keep practicing and applying these concepts to deepen your mathematical knowledge and skills.
Video giới thiệu về cách đơn giản hóa căn bậc hai của 49, hướng dẫn chi tiết và dễ hiểu, phù hợp cho học sinh và người mới bắt đầu.
Căn Bậc Hai của 49
READ MORE:
Video hướng dẫn cách tính căn bậc hai của 49, giải thích chi tiết và dễ hiểu, lý tưởng cho học sinh và người mới bắt đầu học toán.
Cách Tính Căn Bậc Hai của 49: Sqrt(49)