Topic what numbers are square numbers: Have you ever wondered what numbers are square numbers? In this article, we will explore the fascinating world of perfect squares, uncovering their properties, examples, and real-life applications. Join us on this mathematical journey to discover how these unique numbers play a crucial role in various fields and everyday life.
Table of Content
- Square Numbers
- Introduction to Square Numbers
- Definition of Square Numbers
- How to Identify Square Numbers
- Square Numbers in Mathematics
- Patterns in Square Numbers
- Square Roots and Their Relationship to Square Numbers
- Applications of Square Numbers
- Historical Significance of Square Numbers
- Square Numbers in Nature
- Square Numbers in Daily Life
- Interesting Facts about Square Numbers
- Common Mistakes and Misconceptions
- Exercises and Practice Problems
- Resources for Further Learning
- YOUTUBE: Khám phá số học và tìm hiểu về các số bình phương qua video 'Số Bình Phương Được Giải Thích'. Video này cung cấp cái nhìn sâu sắc và dễ hiểu về các số bình phương và ứng dụng của chúng.
Square Numbers
A square number, also known as a perfect square, is a number that can be expressed as the product of an integer with itself. For example, 1, 4, 9, 16, and 25 are square numbers because they can be written as \(1^2\), \(2^2\), \(3^2\), \(4^2\), and \(5^2\) respectively.
Properties of Square Numbers
- Square numbers are always non-negative.
- The square of an even number is always even.
- The square of an odd number is always odd.
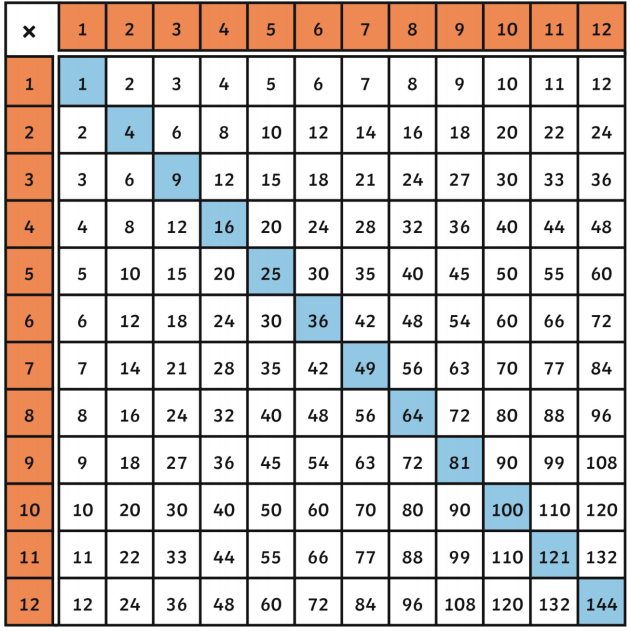
- Square numbers can be visualized as squares with dots forming equal rows and columns.
Examples of Square Numbers
| Number | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
Two-Digit and Three-Digit Square Numbers
There are only six two-digit square numbers: 16, 25, 36, 49, 64, and 81.
There are 22 three-digit square numbers including 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, and 961.
Sum of Square Numbers
The sum of the first \( n \) square numbers can be calculated using the formula:
\[
\sum_{k=1}^{n} k^2 = \frac{n(n+1)(2n+1)}{6}
\]
For example, the sum of the first 6 square numbers is \( 1 + 4 + 9 + 16 + 25 + 36 = 91 \).
Interesting Facts
- The difference between the squares of consecutive numbers is an odd number.
- Square numbers are related to triangular numbers through the formula \( n^2 = T_{2n-1} - T_{n-1} \).
- A square number can be represented geometrically as a square array of dots.
Visualization of Square Numbers
Square numbers can be visualized using arrays. For example, a square number 9 can be visualized as:
| * | * | * |
| * | * | * |
| * | * | * |
Conclusion
Square numbers are fundamental in mathematics, with various properties and applications in different fields. Understanding and recognizing square numbers can be useful for solving a variety of mathematical problems.
READ MORE:
Introduction to Square Numbers
Square numbers, also known as perfect squares, are the product of an integer multiplied by itself. These numbers hold a special place in mathematics due to their unique properties and patterns. To better understand square numbers, let's explore their definition, examples, and key characteristics.
Definition: A square number is an integer that can be expressed as \( n^2 \), where \( n \) is any integer. This means that when you multiply an integer by itself, the resulting product is a square number.
Examples: Here are a few examples of square numbers:
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- \( 5^2 = 25 \)
- \( 6^2 = 36 \)
- \( 7^2 = 49 \)
- \( 8^2 = 64 \)
- \( 9^2 = 81 \)
- \( 10^2 = 100 \)
Properties of Square Numbers:
- Square numbers are always non-negative.
- The square of an even number is even, and the square of an odd number is odd.
- Square numbers grow rapidly as the base integer increases.
- They have an odd number of total factors.
- The difference between consecutive square numbers increases as the numbers increase.
Patterns: Square numbers exhibit interesting patterns. For example, the difference between consecutive square numbers forms an arithmetic sequence of odd numbers:
| \( n \) | \( n^2 \) | Difference (\( (n+1)^2 - n^2 \)) |
| 1 | 1 | 3 |
| 2 | 4 | 5 |
| 3 | 9 | 7 |
| 4 | 16 | 9 |
| 5 | 25 | 11 |
Understanding these properties and patterns helps in recognizing and working with square numbers effectively. In the next sections, we will delve deeper into the significance and applications of square numbers in various fields.
Definition of Square Numbers
Square numbers, also known as perfect squares, are integers that are the product of an integer multiplied by itself. This means a square number can be written in the form \( n^2 \), where \( n \) is an integer. Understanding square numbers is fundamental in mathematics as they form the basis for various mathematical concepts and applications.
To define square numbers more formally:
- A square number is any number that can be represented as \( n^2 \), where \( n \) is an integer.
- This integer \( n \) is called the square root of the square number.
- Square numbers are always non-negative since the product of any integer with itself is non-negative.
Examples of Square Numbers:
| \( n \) | \( n^2 \) |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
In summary, square numbers are special integers that result from multiplying a number by itself. These numbers play a significant role in mathematics and appear frequently in various mathematical problems and real-life applications.
How to Identify Square Numbers
Identifying square numbers involves recognizing numbers that can be expressed as the product of an integer with itself. Here are some steps and methods to determine if a number is a square number:
- Prime Factorization Method:
Perform the prime factorization of the number. If all the prime factors have even exponents, the number is a square number. For example:
- 36: \(36 = 2^2 \times 3^2\) (both exponents are even, so 36 is a square number)
- 50: \(50 = 2^1 \times 5^2\) (not all exponents are even, so 50 is not a square number)
- Square Root Method:
Calculate the square root of the number. If the square root is an integer, then the number is a square number. For example:
- 49: \(\sqrt{49} = 7\) (an integer, so 49 is a square number)
- 20: \(\sqrt{20} \approx 4.47\) (not an integer, so 20 is not a square number)
- Visual Representation:
Visualize the number as a square grid of dots. If you can form a perfect square, the number is a square number. For example:
- 9 can be arranged as a 3x3 grid
- 16 can be arranged as a 4x4 grid
- Sum of Odd Numbers:
Check if the number can be expressed as the sum of consecutive odd numbers starting from 1. For example:
- 16: \(1 + 3 + 5 + 7 = 16\) (so 16 is a square number)
- 18: \(1 + 3 + 5 + 7 + 9\) (does not sum to 18, so 18 is not a square number)
- Digital Root Method:
Find the digital root of the number (sum of its digits until a single digit is obtained). If the digital root is 1, 4, 7, or 9, the number might be a square number. This method is less definitive but can be a quick check. For example:
- 49: \(4 + 9 = 13\), \(1 + 3 = 4\) (digital root is 4, so 49 might be a square number)
- 50: \(5 + 0 = 5\) (digital root is 5, so 50 is not a square number)
By using these methods, you can effectively identify square numbers and understand their unique properties and significance in mathematics.
Square Numbers in Mathematics
Square numbers play a crucial role in various branches of mathematics. They appear in numerous mathematical concepts, theorems, and real-world applications. Let's explore their significance step by step:
- Basic Algebra:
Square numbers are fundamental in algebra. They are used in equations, expressions, and inequalities. For example, solving quadratic equations often involves finding the square roots of square numbers.
- Equation: \( x^2 = 49 \)
- Solution: \( x = \pm 7 \)
- Geometry:
In geometry, square numbers are essential in calculating areas. The area of a square is given by the side length squared. For example:
- If the side length of a square is 5 units, its area is \( 5^2 = 25 \) square units.
- Pythagorean Theorem:
Square numbers are integral to the Pythagorean theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. For example:
- If the legs of the triangle are 3 and 4 units, the hypotenuse is \( \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \) units.
- Number Theory:
Square numbers are prominent in number theory. They are used in various theorems and properties related to integers. For example, Fermat's Last Theorem states that there are no three positive integers \( a \), \( b \), and \( c \) that satisfy \( a^n + b^n = c^n \) for any integer value of \( n \) greater than 2.
- Sequences and Series:
Square numbers form specific sequences, such as the sequence of perfect squares: 1, 4, 9, 16, 25, and so on. These sequences have unique properties and patterns that are studied in mathematics.
- Graph Theory:
In graph theory, square numbers are used to solve problems related to graph coloring, network flows, and more. For example, certain types of graphs, like complete graphs, have properties that involve square numbers.
- Combinatorics:
Square numbers appear in combinatorial problems, such as counting the number of ways to arrange objects in a grid or lattice. These problems often involve calculating permutations and combinations that include square numbers.
Overall, square numbers are a vital part of mathematics, providing a foundation for various concepts, theories, and practical applications. Their properties and patterns help mathematicians solve complex problems and understand the underlying structure of mathematical phenomena.

Patterns in Square Numbers
Square numbers exhibit fascinating patterns that are helpful in various mathematical analyses. Recognizing these patterns can provide deeper insights into the properties and behavior of square numbers. Here are some notable patterns:
- Sum of Odd Numbers:
Every square number is the sum of consecutive odd numbers starting from 1. For example:
- \(1^2 = 1\)
- \(2^2 = 1 + 3 = 4\)
- \(3^2 = 1 + 3 + 5 = 9\)
- \(4^2 = 1 + 3 + 5 + 7 = 16\)
- Difference Between Consecutive Squares:
The difference between the squares of consecutive integers follows a linear pattern. For example:
- \(2^2 - 1^2 = 4 - 1 = 3\)
- \(3^2 - 2^2 = 9 - 4 = 5\)
- \(4^2 - 3^2 = 16 - 9 = 7\)
- \(5^2 - 4^2 = 25 - 16 = 9\)
The difference increases by 2 as we move to the next pair of consecutive squares.
- Last Digits of Square Numbers:
Square numbers exhibit specific patterns in their last digits. The last digit of a square number can only be 0, 1, 4, 5, 6, or 9. For example:
- \(1^2 = 1\)
- \(2^2 = 4\)
- \(3^2 = 9\)
- \(4^2 = 16\)
- \(5^2 = 25\)
- Sum of First \( n \) Square Numbers:
The sum of the first \( n \) square numbers is given by the formula:
\[ \sum_{k=1}^{n} k^2 = \frac{n(n+1)(2n+1)}{6} \]
For example, the sum of the first 3 square numbers:
- \(1^2 + 2^2 + 3^2 = 1 + 4 + 9 = 14\)
- Using the formula: \(\frac{3(3+1)(2 \cdot 3 + 1)}{6} = \frac{3 \cdot 4 \cdot 7}{6} = 14\)
- Geometric Patterns:
Square numbers can be visually represented as perfect squares in a geometric grid. For instance, 9 can be visualized as a 3x3 grid of dots.
Understanding these patterns can enhance problem-solving skills and provide a deeper appreciation of the beauty and structure inherent in mathematics. Square numbers, with their unique and predictable patterns, play a significant role in various mathematical disciplines.
Square Roots and Their Relationship to Square Numbers
The concept of square roots is closely tied to square numbers. Understanding their relationship is essential in various mathematical contexts. Here, we explore the nature of square roots and their connection to square numbers, step by step:
- Definition of Square Roots:
The square root of a number \( n \) is a value \( x \) such that \( x^2 = n \). It is denoted as \( \sqrt{n} \). For example:
- The square root of 25 is \( \sqrt{25} = 5 \), because \( 5^2 = 25 \).
- The square root of 49 is \( \sqrt{49} = 7 \), because \( 7^2 = 49 \).
- Properties of Square Roots:
- Every positive number \( n \) has two square roots: \( \sqrt{n} \) and \( -\sqrt{n} \). For example, \( \sqrt{16} = 4 \) and \( -\sqrt{16} = -4 \).
- The square root of 0 is 0.
- Negative numbers do not have real square roots, as the square of a real number is always non-negative.
- Relationship to Square Numbers:
Square numbers are the result of squaring integers. Consequently, the square root of a square number is always an integer. For example:
- \( \sqrt{1} = 1 \), \( \sqrt{4} = 2 \), \( \sqrt{9} = 3 \)
- \( \sqrt{16} = 4 \), \( \sqrt{25} = 5 \), \( \sqrt{36} = 6 \)
- Calculating Square Roots:
Square roots can be calculated using various methods:
- Prime Factorization: Factor the number into its prime factors and pair them to find the square root. For example:
- \( 144 = 2^4 \times 3^2 \). Pairing the factors, we get \( (2^2 \times 3)^2 = 12^2 \). Hence, \( \sqrt{144} = 12 \).
- Long Division Method: A manual method that provides an iterative approach to finding square roots.
- Using a Calculator: Modern calculators have a built-in square root function for quick calculations.
- Prime Factorization: Factor the number into its prime factors and pair them to find the square root. For example:
- Applications of Square Roots:
Square roots have numerous applications in various fields:
- Geometry: Used to calculate the side lengths of squares and right-angled triangles.
- Physics: Appear in equations involving energy, velocity, and acceleration.
- Statistics: Used in formulas to calculate standard deviations and variances.
Understanding square roots and their relationship to square numbers is fundamental in mathematics. Recognizing the properties and applications of square roots can enhance problem-solving skills and provide a deeper appreciation for mathematical concepts.
Applications of Square Numbers
Square numbers have a wide range of applications in various fields including mathematics, geometry, computer science, and even in everyday life. Here are some detailed applications of square numbers:
1. Geometry and Area Calculation
In geometry, the concept of square numbers is directly used to calculate the area of squares. The area of a square is given by the formula:
\[ \text{Area} = \text{side} \times \text{side} = \text{side}^2 \]
For example, a square with a side length of 5 units has an area of:
\[ 5 \times 5 = 25 \text{ square units} \]
2. Computer Science and Algorithms
Square numbers play a crucial role in computer science, particularly in algorithms related to sorting and searching. For example, the time complexity of certain algorithms, such as bubble sort and insertion sort, can be represented in terms of square numbers (O(n^2)). Additionally, memory allocation and data structure arrangements often utilize square numbers for efficient storage and retrieval.
3. Physics and Engineering
In physics, square numbers are used in the calculation of areas and in various formulas involving energy and force. For instance, the formula for the kinetic energy of an object is:
\[ E_k = \frac{1}{2}mv^2 \]
Here, the velocity (v) is squared, illustrating the importance of square numbers in physical computations.
4. Financial Calculations
In finance, square numbers are used in the calculation of interest rates, especially when dealing with compound interest. The formula for compound interest involves squaring the growth factor over multiple periods.
\[ A = P \left(1 + \frac{r}{n}\right)^{nt} \]
Where \(A\) is the amount, \(P\) is the principal, \(r\) is the rate, \(n\) is the number of times interest is compounded per year, and \(t\) is the time the money is invested for. In this context, the exponentiation involves square numbers for multiple periods.
5. Patterns in Nature
Square numbers appear in various patterns in nature. For example, the arrangement of certain types of leaves and petals, as well as the structure of crystals, can often be described using square numbers. Additionally, square numbers are seen in the formation of certain plant growth patterns and animal markings.
6. Educational Tools
Square numbers are fundamental in education, especially in teaching multiplication and understanding number patterns. They help students grasp the concept of area and the properties of numbers. Educational tools such as multiplication tables and number grids often highlight square numbers to show their unique properties and relationships.
7. Everyday Life
In daily life, square numbers are used in various practical situations such as flooring, tiling, and fabric cutting, where the dimensions of squares are essential for accurate measurement and resource optimization. For instance, knowing that 16 square tiles will perfectly fit a 4x4 area helps in planning and resource allocation.
Overall, square numbers are a fundamental mathematical concept with diverse applications that extend far beyond simple arithmetic, influencing various scientific and practical fields.
Historical Significance of Square Numbers
Square numbers have held a significant place in the history of mathematics and philosophy. From the ancient Greeks to modern times, these numbers have fascinated mathematicians and scholars.
The ancient Greeks, particularly the Pythagoreans, were deeply intrigued by the properties of numbers and their geometric representations. They often arranged pebbles in shapes to explore arithmetical and mystical relationships. Square numbers, represented by pebbles forming perfect squares, were seen as fundamental and harmonious. For instance, arranging 1, 4, 9, and 16 pebbles into squares visually demonstrated the concept of squaring a number.
The Pythagoreans attributed significant symbolic meanings to square numbers. They believed these numbers embodied perfection and symmetry. This philosophical perspective extended to various aspects of life and nature, where they sought to find numerical harmony and order. Their fascination with numerical relationships also led to the discovery of the connection between musical harmony and simple whole-number ratios.
In the Middle Ages, the study of square numbers continued to evolve. Mathematicians like Fibonacci explored the properties of square numbers and their applications in solving problems. The introduction of algebra provided new tools to study these numbers, leading to significant advancements in number theory.
One of the most notable contributions to the understanding of square numbers came from Pierre de Fermat, who proposed Fermat's Last Theorem. Although the theorem itself does not directly involve square numbers, Fermat's work laid the groundwork for future mathematicians like Euler and Lagrange to explore the properties of squares and their sums.
Joseph-Louis Lagrange's Four-Square Theorem, proposed in 1770, was a major milestone in number theory. It states that every positive integer can be represented as the sum of at most four square numbers. This theorem not only highlighted the versatility of square numbers but also had profound implications in various mathematical fields, including the study of Diophantine equations.
In modern times, square numbers continue to play a crucial role in various mathematical and applied fields. They are fundamental in algebra, geometry, and calculus. Additionally, square numbers are essential in computer science, particularly in algorithms and cryptography.
The historical significance of square numbers is a testament to their enduring appeal and foundational importance in the development of mathematical thought. From ancient philosophical musings to modern scientific applications, square numbers remain a cornerstone of mathematical exploration and discovery.

Square Numbers in Nature
Square numbers appear in various forms in nature, illustrating the inherent mathematical structure of the natural world. Here are some fascinating examples and patterns:
- Patterns in Plant Growth: Many plants exhibit growth patterns that can be related to square numbers. For instance, the arrangement of leaves, petals, and seeds often follows a geometric progression, optimizing space and exposure to sunlight. The Fibonacci sequence, which closely relates to square numbers, is observed in the spiral patterns of sunflowers, pine cones, and pineapples.
- Animal Markings: The markings on certain animals, such as the spots on a leopard or the scales on a fish, often form patterns that can be broken down into square grids. This geometric distribution helps in camouflage and heat regulation.
- Crystal Structures: The molecular structure of crystals, such as salt (NaCl) and diamond, often forms cubic or square lattice structures. These arrangements result from the way atoms bond and align in a repeating pattern, minimizing energy and maximizing stability.
- Geological Formations: Natural formations like columnar basalt, seen in the Giant's Causeway in Northern Ireland, form hexagonal and square cross-sections due to the cooling and fracturing processes of volcanic rock.
Square numbers, defined as the product of an integer multiplied by itself (e.g., 1, 4, 9, 16), manifest in these natural phenomena due to their inherent efficiency and balance. The presence of these numbers in nature highlights the fundamental role of mathematics in shaping the world around us.
Square Numbers in Daily Life
Square numbers, also known as perfect squares, are numbers that can be expressed as the product of an integer with itself. These numbers have various applications in our daily lives, often simplifying calculations and providing useful patterns. Here are some ways square numbers are relevant in everyday contexts:
- Architecture and Construction: Square numbers are frequently used in architecture and construction. For example, when determining the area of square-shaped rooms or materials, square numbers help simplify the calculations. If a room has sides of 4 meters, the area is \(4 \times 4 = 16\) square meters.
- Gardening: Square numbers help in gardening, particularly in the layout of plants. Gardeners often use square grids to space plants evenly. For instance, planting in a 3x3 grid ensures that nine plants are evenly spaced.
- Technology: In digital imaging and screen resolutions, square numbers are significant. Common screen resolutions like 1024x1024 pixels or 2048x2048 pixels are based on square numbers, ensuring uniform and high-quality displays.
- Games and Puzzles: Square numbers often appear in games and puzzles, including Sudoku, where the standard grid size is 9x9, a perfect square of 81. These grids help in organizing and solving such puzzles efficiently.
- Sports: Square numbers are used in various sports statistics and fields. For instance, in chess, the board is an 8x8 grid, totaling 64 squares, making it a square number that facilitates the game's structure.
- Home Décor and Design: Square numbers assist in home décor, particularly in tile design and flooring. If you need to tile a square area with 4x4 tiles, you will need \(4 \times 4 = 16\) tiles, ensuring a precise and neat finish.
- Mathematics and Education: Understanding square numbers is crucial in education, as they form the foundation for more complex mathematical concepts. Recognizing and using square numbers can make learning and applying mathematical principles easier and more intuitive.
- Financial Planning: Square numbers help in financial calculations, such as estimating compound interest over time. For instance, if an investment doubles every period (a simplified model), the growth pattern can be represented using square numbers, illustrating exponential growth.
Square numbers are more than just mathematical curiosities; they are practical tools that make various aspects of our daily lives more manageable and efficient. Their presence in architecture, technology, education, and beyond showcases their fundamental importance in our world.
Interesting Facts about Square Numbers
Square numbers, also known as perfect squares, are integers that can be expressed as the product of an integer with itself. Here are some interesting facts about square numbers:
-
Pattern in Odd Numbers: The square of any integer \( n \) can be represented as the sum of the first \( n \) odd numbers. For example:
- \(2^2 = 4 = 1 + 3\)
- \(3^2 = 9 = 1 + 3 + 5\)
- \(4^2 = 16 = 1 + 3 + 5 + 7\)
-
Sum of First \( n \) Squares: The sum of the first \( n \) square numbers can be calculated using the formula:
\[\sum_{i=1}^{n} i^2 = \frac{n(n + 1)(2n + 1)}{6}\]
For example, the sum of the first 3 square numbers is:
\[\sum_{i=1}^{3} i^2 = 1^2 + 2^2 + 3^2 = 1 + 4 + 9 = 14\]
-
Even and Odd Squares: The square of an even number is always even, and the square of an odd number is always odd. For instance:
- The square of 4 (even) is 16 (even).
- The square of 5 (odd) is 25 (odd).
-
Ending Digits: Square numbers end with specific digits. A square number can end in 0, 1, 4, 5, 6, or 9, but never in 2, 3, 7, or 8.
-
Difference Between Squares: The difference between consecutive square numbers follows a pattern:
\[(n+1)^2 - n^2 = 2n + 1\]
For example, the difference between \(4^2\) and \(3^2\) is:
\[4^2 - 3^2 = 16 - 9 = 7 = 2 \cdot 3 + 1\]
-
Geometric Representation: A number is a square number if you can arrange that many points to form a perfect square. For example, 9 points can be arranged in a 3x3 grid.
-
Historical Insight: The concept of square numbers was known to ancient civilizations, including the Greeks, who used them to study geometric properties and number theory.
-
Sum of Squares of Two Consecutive Numbers: Any square number is the sum of two consecutive triangular numbers. For instance:
\[n^2 = T_n + T_{n-1}\]
where \(T_n\) is the \(n\)-th triangular number.
Common Mistakes and Misconceptions
Understanding and identifying common mistakes and misconceptions about square numbers can help avoid errors and deepen comprehension. Here are some frequent issues and how to address them:
-
Confusing Square Numbers with Other Types of Numbers:
Some learners might mistake square numbers for perfect cubes or simply for larger even numbers. It's essential to remember that a square number is the product of an integer multiplied by itself, such as \(4 = 2^2\) or \(9 = 3^2\).
-
Incorrectly Identifying Non-Square Numbers:
Students might incorrectly identify numbers as squares without checking if they result from squaring an integer. For example, 8 and 12 are often mistaken as square numbers because they are close to 9 and 16. Ensure students verify by checking if the square root of a number is an integer.
-
Errors in Arithmetic Operations:
Sometimes, errors arise from basic arithmetic mistakes, such as incorrectly calculating squares or square roots. Reinforce the importance of accurate calculation by practicing operations and double-checking work.
-
Misunderstanding the Properties of Square Numbers:
Students might not fully grasp properties such as the fact that the sum of the first \(n\) odd numbers is always a square number, or that square numbers can only have an odd number of total divisors.
-
Forgetting to Consider Negative Numbers:
Since squaring a negative number results in a positive number, learners might overlook that both positive and negative roots exist for any given square number. For instance, both \(3\) and \(-3\) are roots of \(9\).
Here are steps to address these misconceptions effectively:
-
Diagnosis:
Identify the specific mistake by having students explain their reasoning. This helps determine if the issue is a simple error or a deeper misunderstanding.
-
Discussion:
Engage students in a discussion about their errors, asking them to explain their thought processes. This encourages them to reflect on their understanding and clarify their misconceptions.
-
Correction:
Provide correct examples and counter-examples. Use visual aids like number lines or charts to illustrate why a certain number is or isn’t a square number.
-
Practice:
Offer plenty of practice problems that target the identified misconceptions. This reinforces correct understanding and builds confidence.
-
Assessment:
Regularly assess understanding through formative assessments to ensure misconceptions have been addressed and corrected.

Exercises and Practice Problems
Practicing square numbers helps reinforce the understanding of their properties and applications. Below are various exercises and practice problems designed to enhance your skills with square numbers.
-
Identify Square Numbers
- Which of the following numbers are square numbers?
- 1, 2, 4, 7, 9, 11, 16, 18, 25, 27, 36
- Find the next five square numbers after 36.
- Which of the following numbers are square numbers?
-
Calculate Squares
- What is \( 5^2 \)?
- Calculate \( 12^2 \).
- Find the square of 15.
- Determine \( 20^2 \).
- What is \( 25^2 \)?
-
Square Roots
- What is the square root of 49?
- Find the square root of 64.
- Determine the square root of 100.
- Calculate the square root of 144.
- What is the square root of 225?
-
Word Problems
- A square garden has an area of 81 square meters. What is the length of one side of the garden?
- A square-shaped field covers an area of 400 square meters. How long is each side of the field?
- The area of a square is 169 square meters. What is the length of each side?
- A square parking lot has an area of 625 square meters. How long is one side of the parking lot?
- The side of a square is 13 meters. What is the area of the square?
-
Pattern Recognition
- Identify the pattern in the following sequence of square numbers and find the next two numbers: 1, 4, 9, 16, 25, 36, __, __.
- Complete the sequence: 64, 81, 100, 121, __, __.
- What is the common difference between successive square numbers in the sequence 1, 4, 9, 16, 25?
These exercises cover a range of problems to help solidify your understanding of square numbers. Practice regularly to master these concepts!
Resources for Further Learning
To deepen your understanding of square numbers and their applications, consider exploring the following resources:
-
Books:
- The Joy of x: A Guided Tour of Math, from One to Infinity by Steven Strogatz - This book offers insights into various mathematical concepts, including square numbers, in an engaging manner.
- Mathematics for the Nonmathematician by Morris Kline - A comprehensive guide for those looking to understand the foundations of mathematics, including properties of square numbers.
-
Online Courses:
- - This course covers the basics of quadratic expressions and square numbers, with interactive exercises.
- - This course helps develop the critical thinking skills needed to approach mathematical problems, including square numbers.
-
Educational Websites:
- - Provides definitions, examples, and practice problems for square numbers.
- - An accessible site with explanations, visual aids, and exercises related to square numbers.
-
Worksheets and Practice Problems:
- - A free downloadable worksheet with over 20 questions, including reasoning and applied problems.
- - Offers a variety of worksheets to practice and master square numbers.
-
Videos:
- - A video explaining the concept of square numbers with examples and visual aids.
- - A comprehensive video that explores both square roots and square numbers.
These resources will help you build a solid foundation in understanding square numbers and their various applications. Happy learning!
Khám phá số học và tìm hiểu về các số bình phương qua video 'Số Bình Phương Được Giải Thích'. Video này cung cấp cái nhìn sâu sắc và dễ hiểu về các số bình phương và ứng dụng của chúng.
Số Học: Số Bình Phương Được Giải Thích
READ MORE:
Khám phá khái niệm về số vuông và cách chúng được xác định trong toán học với FuseSchool. Tìm hiểu thêm về số học qua video này.
Số Vuông Là Gì | Số Học | Toán Học | FuseSchool