Topic x squared derivative: The derivative of x squared, denoted as \( \frac{d}{dx} (x^2) = 2x \), is a fundamental concept in calculus. This article explores its derivation methods, practical applications, and importance in various fields such as physics and engineering. Understanding this concept enhances problem-solving skills in velocity, acceleration, and optimization problems.
Table of Content
- Understanding the Derivative of x2
- Introduction
- Definition of Derivative
- Formula for the Derivative of x Squared
- Methods to Derive x Squared
- Applications of the Derivative of x Squared
- Proofs of the Derivative of x Squared
- Higher-Order Derivatives
- Using Derivative Calculators
- YOUTUBE: Video này trình bày một cách trực quan về đạo hàm của hàm số x bình phương.
Understanding the Derivative of x2
The derivative of a function gives the rate at which the function value changes as its input changes. For the function \( f(x) = x^2 \), its derivative can be found using various methods. Here, we will explore the derivative of \( x^2 \) using the power rule, first principles, and graphical interpretation.
Derivative of x2 using the Power Rule
The power rule states that for any function of the form \( f(x) = x^n \), the derivative is given by \( f'(x) = nx^{n-1} \). Applying this to \( x^2 \):
\[
\frac{d}{dx} (x^2) = 2x
\]
Thus, the derivative of \( x^2 \) is \( 2x \).
Derivative of x2 from First Principles
The first principles approach involves calculating the derivative from the definition of the limit. For \( f(x) = x^2 \):
\[
f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}
\]
Substituting \( x^2 \) into the formula:
\[
f'(x) = \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} = \lim_{h \to 0} \frac{x^2 + 2xh + h^2 - x^2}{h} = \lim_{h \to 0} \frac{2xh + h^2}{h} = \lim_{h \to 0} (2x + h) = 2x
\]
So, using first principles, the derivative of \( x^2 \) is also \( 2x \).
Graphical Interpretation
Graphically, the derivative represents the slope of the tangent line to the curve at any given point. For \( f(x) = x^2 \), the slope at any point \( x \) is \( 2x \). Below is a table showing the slopes at various points:
| x | f'(x) = 2x |
|---|---|
| -2 | -4 |
| -1 | -2 |
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
The graph of \( x^2 \) with tangent lines at different points confirms that the slopes match the calculated values.
Conclusion
Whether using the power rule, first principles, or graphical interpretation, the derivative of \( x^2 \) consistently results in \( 2x \). Understanding these methods provides a deeper insight into calculus and the behavior of functions.
For more detailed examples and proofs, you can explore further using online derivative calculators and educational resources.

READ MORE:
Introduction
The derivative of x squared, denoted as d/dx (x^2), is a fundamental concept in calculus that measures the rate of change of the function x^2 with respect to the variable x. This concept is crucial in understanding various mathematical and real-world applications, such as calculating velocity, acceleration, and optimizing functions.
To find the derivative of x squared, we apply the power rule of differentiation. The power rule states that the derivative of x^n is n*x^(n-1). Using this rule, we find that the derivative of x^2 is 2x. This result can also be derived using different methods such as the first principle, the product rule, and the quotient rule.
By understanding the derivative of x squared, we gain insights into the behavior of quadratic functions and their applications in different fields. The calculation of derivatives is an essential skill for solving problems in physics, engineering, economics, and many other disciplines.
Definition of Derivative
The derivative of a function measures how the function value changes as its input changes. It is a fundamental concept in calculus, representing an instantaneous rate of change. The derivative of a function \( f(x) \) with respect to \( x \) is denoted as \( f'(x) \) or \( \frac{d}{dx}f(x) \).
To define the derivative formally, we use the limit process:
\[
f'(x) = \lim_{{h \to 0}} \frac{f(x+h) - f(x)}{h}
\]
This formula calculates the slope of the tangent line to the curve of the function \( f(x) \) at any point \( x \). The limit ensures that the difference quotient approaches the exact rate of change as \( h \) (the difference between \( x \) and a nearby point) approaches zero.
For a power function like \( x^2 \), the derivative is computed using the power rule, which states:
\[
\frac{d}{dx}x^n = nx^{n-1}
\]
Applying this rule to \( x^2 \), we get:
\[
\frac{d}{dx}x^2 = 2x
\]
Thus, the derivative of \( x^2 \) is \( 2x \), indicating that the rate of change of \( x^2 \) with respect to \( x \) is proportional to \( x \) itself, scaled by a factor of 2.
Formula for the Derivative of x Squared
The derivative of \( x^2 \) is a fundamental concept in calculus. It is calculated using the power rule for derivatives. The power rule states that the derivative of \( x^n \) is \( nx^{n-1} \). Applying this to \( x^2 \), we get:
\[
\frac{d}{dx} (x^2) = 2x
\]
This formula represents the rate of change of the function \( x^2 \) with respect to \( x \). Here is a step-by-step derivation:
- Start with the function \( f(x) = x^2 \).
- According to the power rule, if \( f(x) = x^n \), then \( f'(x) = nx^{n-1} \).
- For \( x^2 \), \( n = 2 \). Thus, \( f'(x) = 2x^{2-1} = 2x \).
Therefore, the derivative of \( x^2 \) is \( 2x \). This result can be proved using various methods such as the first principle, product rule, and quotient rule.
Using the First Principle
The first principle of derivatives, also known as the limit definition, can be used to find the derivative of \( x^2 \). The formula is:
\[
f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}
\]
For \( f(x) = x^2 \):
\[
f'(x) = \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} = \lim_{h \to 0} \frac{x^2 + 2xh + h^2 - x^2}{h} = \lim_{h \to 0} \frac{2xh + h^2}{h} = \lim_{h \to 0} (2x + h) = 2x
\]
Using the Product Rule
The product rule states that the derivative of a product of two functions is given by:
\[
(uv)' = u'v + uv'
\]
For \( x^2 \), consider it as \( x \cdot x \):
\[
f'(x) = \frac{d}{dx} (x \cdot x) = \frac{d}{dx} (x) \cdot x + x \cdot \frac{d}{dx} (x) = 1 \cdot x + x \cdot 1 = x + x = 2x
\]
Using the Quotient Rule
The quotient rule is used for finding the derivative of a quotient of two functions. It is given by:
\[
\left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2}
\]
For \( x^2 \), we can write it as \( \frac{x^2}{1} \):
\[
f'(x) = \frac{1 \cdot \frac{d}{dx}(x^2) - x^2 \cdot \frac{d}{dx}(1)}{1^2} = \frac{1 \cdot 2x - x^2 \cdot 0}{1} = 2x
\]
Hence, using different methods, we arrive at the same result: the derivative of \( x^2 \) is \( 2x \).
Methods to Derive x Squared
The derivative of \(x^2\) can be derived using several methods, each providing a unique approach to understanding differentiation. Here are the most common methods:
- First Principle of Derivatives:
The first principle, also known as the delta method, involves finding the general expression for the slope of a curve using algebra. The derivative of \(x^2\) is determined as follows:
- Start with the definition of the derivative: \[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \]
- Substitute \(f(x) = x^2\): \[ f'(x) = \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} \]
- Simplify the expression: \[ f'(x) = \lim_{h \to 0} \frac{x^2 + 2xh + h^2 - x^2}{h} = \lim_{h \to 0} \frac{2xh + h^2}{h} = \lim_{h \to 0} (2x + h) \]
- As \(h\) approaches 0, the derivative is: \[ f'(x) = 2x \]
- Product Rule:
The product rule is used when \(x^2\) is expressed as the product of two functions \(x \cdot x\). The product rule states that:
\([uv]' = u'v + uv'\)
- Set \(u = x\) and \(v = x\).
- Apply the product rule: \[ (x^2)' = (x \cdot x)' = x' \cdot x + x \cdot x' = 1 \cdot x + x \cdot 1 = x + x \]
- Simplify to get: \[ f'(x) = 2x \]
- Quotient Rule:
Although less common for \(x^2\), the quotient rule can also be applied. The quotient rule states:
\[ \left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2} \]
- Express \(x^2\) as a quotient: \( x^2 = \frac{x^2}{1} \)
- Set \(u = x^2\) and \(v = 1\).
- Apply the quotient rule: \[ \left( \frac{x^2}{1} \right)' = \frac{(x^2)' \cdot 1 - x^2 \cdot 0}{1^2} = \frac{2x \cdot 1}{1} = 2x \]
Each of these methods confirms that the derivative of \(x^2\) is \(2x\), providing multiple approaches to understanding the differentiation process.
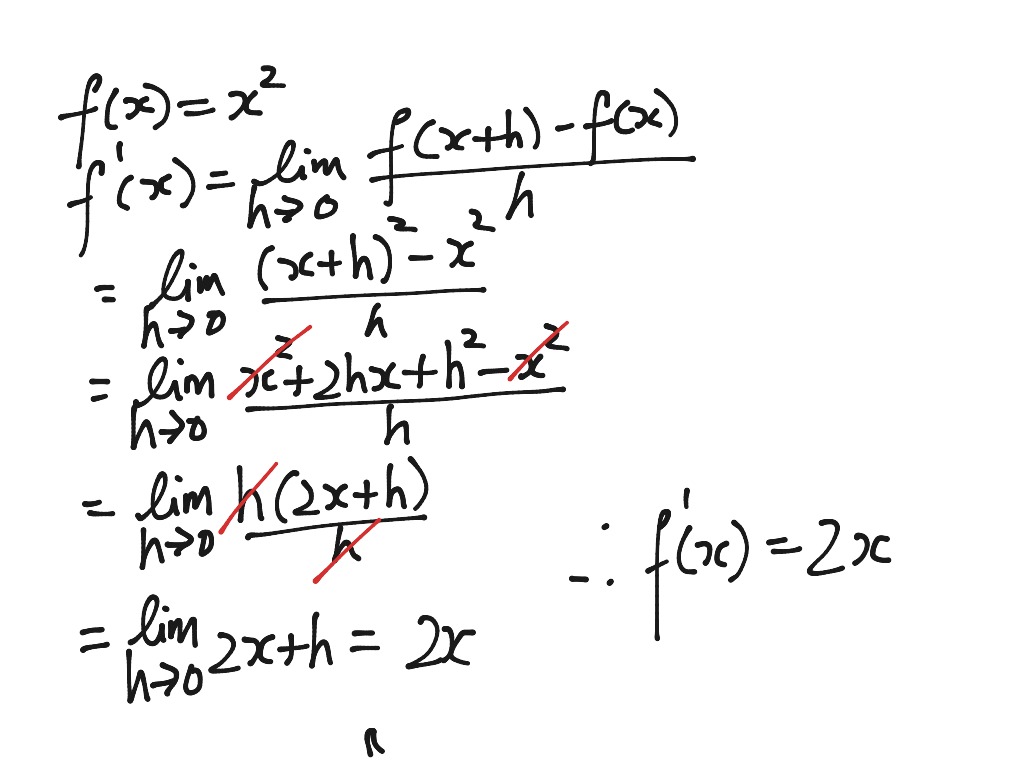
Applications of the Derivative of x Squared
The derivative of \(x^2\), which is \(2x\), has numerous practical applications across various fields. Below, we explore several key areas where this derivative plays a crucial role:
- Physics: In physics, the derivative of \(x^2\) is often used to calculate velocity and acceleration. For example, if \(x(t)\) represents the position of an object as a function of time, then \(2x\) represents its instantaneous velocity.
- Economics: In economics, the derivative of \(x^2\) can be applied to cost functions. If the cost to produce \(x\) units of a product is given by a quadratic function, the derivative helps determine the marginal cost, which is the cost of producing one additional unit.
- Engineering: Engineers use the derivative of \(x^2\) in various analyses, including stress and strain calculations in materials, where the quadratic relationship between variables can be differentiated to find rates of change and optimize performance.
- Optimization: The derivative of \(x^2\) is fundamental in optimization problems. By setting the derivative equal to zero, we can find critical points that help in identifying minimum or maximum values of functions, which is essential in fields like operations research and logistics.
- Computer Science: In computer graphics and machine learning, derivatives, including that of \(x^2\), are used in algorithms for optimization and modeling. Gradient descent, a popular optimization algorithm, utilizes derivatives to minimize error functions.
These applications demonstrate the versatility and importance of understanding the derivative of \(x^2\) in both theoretical and practical contexts.
Proofs of the Derivative of x Squared
The derivative of \( x^2 \) can be proven using several methods. Below are detailed proofs that illustrate different approaches to derive this fundamental result.
-
Using the Definition of Derivative:
The derivative of a function \( f(x) \) is given by the limit definition:
\[
f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}
\]For \( f(x) = x^2 \), we have:
\[
f'(x) = \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} = \lim_{h \to 0} \frac{x^2 + 2xh + h^2 - x^2}{h} = \lim_{h \to 0} \frac{2xh + h^2}{h} = \lim_{h \to 0} (2x + h) = 2x
\] -
Using the Power Rule:
The power rule states that the derivative of \( x^n \) is given by:
\[
\frac{d}{dx} x^n = n x^{n-1}
\]For \( n = 2 \), applying the power rule directly yields:
\[
\frac{d}{dx} x^2 = 2 x^{2-1} = 2x
\] -
Geometric Interpretation:
Consider a point \( (x, x^2) \) on the curve and another point close to it, \( (x+h, (x+h)^2) \). The slope of the line connecting these points is:
\[
m = \frac{\Delta y}{\Delta x} = \frac{(x+h)^2 - x^2}{h} = \frac{2xh + h^2}{h} = 2x + h
\]As \( h \) approaches zero, the slope converges to \( 2x \), which is the derivative of \( x^2 \).
Higher-Order Derivatives
The second derivative of \( f(x) = x^2 \) is calculated as follows:
\( f'(x) = 2x \) \( f''(x) = \frac{d}{dx}[2x] = 2 \) Thus, the second derivative \( f''(x) \) of \( x^2 \) is 2.
Higher-order derivatives of \( x^2 \) can be computed recursively:
\( f'''(x) = \frac{d}{dx}[2] = 0 \) \( f^{(4)}(x) = \frac{d}{dx}[0] = 0 \) ... For \( n \geq 2 \), \( f^{(n)}(x) = 0 \) for all even \( n \) (derivatives of even order) and \( f^{(n)}(x) = 2 \cdot (n-1)! \) for all odd \( n \) (derivatives of odd order).
Using Derivative Calculators
Derivative calculators are online tools that compute derivatives of functions, including \( x^2 \), quickly and accurately.
They use algorithms based on calculus rules such as the power rule, product rule, quotient rule, and chain rule to calculate derivatives.
Users input the function \( x^2 \) or any other function, and the calculator provides step-by-step solutions or immediate results.
These tools are useful for students learning calculus, professionals needing quick derivations, and anyone needing to verify their calculus work.
Most derivative calculators offer additional features like graphing capabilities and the ability to compute higher-order derivatives.

Video này trình bày một cách trực quan về đạo hàm của hàm số x bình phương.
Biến thể hình ảnh của đạo hàm của x bình phương
READ MORE:
Video này giải thích tại sao đạo hàm của hàm số x bình phương bằng 2x.
Tại sao đạo hàm của x^2 = 2x?

:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)




