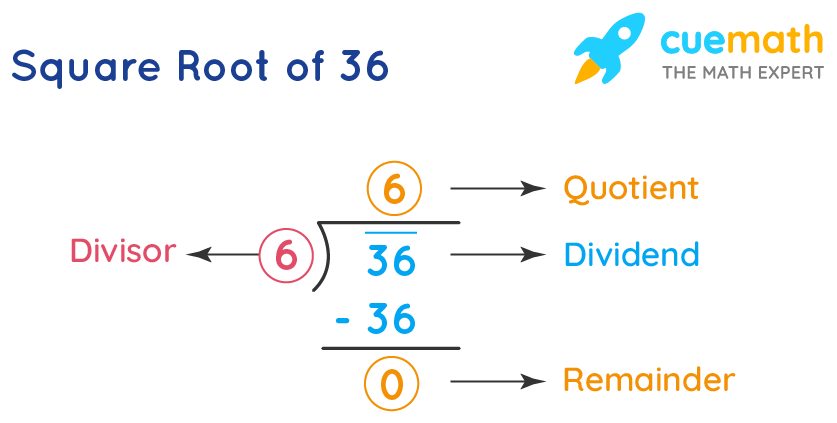Topic what is the square root of negative 36: Discovering the square root of negative 36 introduces us to the fascinating world of complex numbers. Unlike positive numbers, the square root of a negative number involves imaginary units. This article will explore what the square root of negative 36 is, how it is calculated, and its significance in mathematics.
Table of Content
- Understanding the Square Root of Negative 36
- Introduction
- Definition of Square Root
- Square Root of Negative Numbers
- Complex Numbers and Imaginary Unit
- Calculation of Square Root of -36
- Properties of Square Root
- Applications and Examples
- Square Root Table
- Frequently Asked Questions
- YOUTUBE: Khám phá căn bậc hai của -36. Video giải thích chi tiết về căn bậc hai của số âm và các khái niệm liên quan.
Understanding the Square Root of Negative 36
To find the square root of negative 36, we need to understand the concept of imaginary numbers. Imaginary numbers are numbers that, when squared, yield a negative result. The imaginary unit is denoted by i, where \( i = \sqrt{-1} \).
Calculation
The square root of negative 36 can be broken down as follows:
\[ \sqrt{-36} = \sqrt{-1 \times 36} = \sqrt{-1} \times \sqrt{36} = i \times 6 = 6i \]
Explanation
- Imaginary Unit: The term \( \sqrt{-1} \) is represented as i, the basic imaginary unit.
- Positive Square Root: The square root of 36 is 6, as \( 6 \times 6 = 36 \).
- Combining Results: Multiplying the results of \( \sqrt{-1} \) and \( \sqrt{36} \) gives us \( 6i \).
Summary
Thus, the square root of -36 is:
\[ \sqrt{-36} = 6i \]

READ MORE:
Introduction
The square root of negative 36, denoted as √-36, is not a real number. In mathematics, when we encounter the square root of a negative number, we use the concept of imaginary numbers. The imaginary unit, represented by i, is defined as the square root of -1. Therefore, the square root of -36 can be expressed using imaginary numbers.
To find the square root of -36, we proceed as follows:
- Recognize that -36 is a negative number, so its square root will involve the imaginary unit i.
- Express -36 as the product of 36 and -1: -36 = 36 * -1.
- Take the square root of each factor separately: √-36 = √(36 * -1) = √36 * √-1.
- Since √36 = 6 and √-1 = i, we combine these results to obtain: √-36 = 6i.
Thus, the square root of -36 is 6i. This means that when 6i is multiplied by itself, the result is -36, demonstrating the concept of imaginary numbers and their application in extending the real number system.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 36 is 6 because \(6^2 = 36\).
When dealing with negative numbers, such as -36, the concept extends to complex numbers. The square root of -36 involves imaginary numbers, and can be expressed as ±6i, where "i" is the imaginary unit (\(i^2 = -1\)).
Let's break this down step by step:
- The square root of a positive number \(x\) is a number \(y\) such that \(y^2 = x\).
- For negative numbers, we use the imaginary unit \(i\), where \(i^2 = -1\).
- Therefore, the square root of -36 is given by \(\sqrt{-36} = \sqrt{36} \times \sqrt{-1} = 6i\).
In summary, the square root of -36 is ±6i, reflecting both the positive and negative roots in the complex plane.
Square Root of Negative Numbers
Understanding the square root of negative numbers requires delving into complex numbers. A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). For positive numbers, this concept is straightforward. However, for negative numbers, we need to introduce the concept of imaginary numbers.
Imaginary numbers are built around the imaginary unit \( i \), where \( i \) is defined as \( \sqrt{-1} \). This means that for any negative number \( -x \), its square root can be expressed as \( \sqrt{-x} = \sqrt{x} \cdot i \).
Let's take the example of \( -36 \):
- Recognize that \( -36 \) is a negative number.
- Express it in terms of its positive counterpart: \( -36 = 36 \cdot -1 \).
- Use the property of square roots: \( \sqrt{-36} = \sqrt{36 \cdot -1} \).
- Separate the terms: \( \sqrt{36} \cdot \sqrt{-1} \).
- Since \( \sqrt{36} = 6 \) and \( \sqrt{-1} = i \), we have: \( \sqrt{-36} = 6i \).
Thus, the square root of \( -36 \) is \( 6i \). This principle applies to all negative numbers, transforming them into imaginary numbers when their square roots are calculated.
| Negative Number | Square Root |
|---|---|
| -1 | i |
| -4 | 2i |
| -9 | 3i |
| -16 | 4i |
| -25 | 5i |
| -36 | 6i |
Understanding these concepts not only helps in solving mathematical problems but also lays the foundation for more advanced topics in complex number theory.
Complex Numbers and Imaginary Unit
Understanding the square root of negative numbers requires the concept of complex numbers and the imaginary unit. The imaginary unit is denoted by \( i \), where \( i \) is defined as \( \sqrt{-1} \). This definition allows us to work with the square roots of negative numbers, which are not possible in the realm of real numbers.
When dealing with the square root of -36, we use the property of the imaginary unit:
- The square root of -36 can be expressed as \( \sqrt{-36} \).
- Using the imaginary unit, this becomes \( \sqrt{36} \times \sqrt{-1} \).
- Since \( \sqrt{36} = 6 \) and \( \sqrt{-1} = i \), we get \( \sqrt{-36} = 6i \).
This shows that the square root of -36 is \( 6i \). Similarly, the negative counterpart is \( -6i \), giving us two complex roots: \( 6i \) and \( -6i \).
Complex numbers are numbers that have both a real part and an imaginary part. They are typically written in the form \( a + bi \), where \( a \) is the real part and \( bi \) is the imaginary part. In our case, the square root of -36 yields purely imaginary numbers because the real part is zero.
Understanding these concepts is fundamental in advanced mathematics and is particularly useful in fields such as engineering and physics where complex numbers are used to solve equations that do not have real solutions.

Calculation of Square Root of -36
The square root of a negative number involves understanding complex numbers and the imaginary unit \(i\), where \(i\) is defined as \(\sqrt{-1}\). Here's a step-by-step guide to calculate the square root of -36:
Identify the negative number under the square root: \(\sqrt{-36}\).
Express the negative number as a product of -1 and a positive number: \(\sqrt{-1 \times 36}\).
Split the square root into the product of two square roots: \(\sqrt{-1} \times \sqrt{36}\).
Substitute the imaginary unit \(i\) for \(\sqrt{-1}\): \(i \times \sqrt{36}\).
Calculate the square root of the positive number: \(i \times 6\).
Combine the results to obtain the final answer: \(6i\).
Therefore, the square roots of -36 are \( \pm 6i \).
Properties of Square Root
The concept of complex numbers is fundamental when dealing with the square root of negative numbers. A complex number is a number of the form \( a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit. The imaginary unit \( i \) is defined as the square root of -1, i.e., \( i = \sqrt{-1} \).
Using this definition, the square root of any negative number can be expressed in terms of \( i \). For example, the square root of -36 can be calculated as follows:
- Rewrite -36 as a product of 36 and -1: \( -36 = 36 \times (-1) \).
- Take the square root of both factors: \( \sqrt{-36} = \sqrt{36 \times (-1)} \).
- Apply the property of square roots: \( \sqrt{36 \times (-1)} = \sqrt{36} \times \sqrt{-1} \).
- Recognize that \( \sqrt{36} = 6 \) and \( \sqrt{-1} = i \): \( \sqrt{-36} = 6i \).
Thus, the square root of -36 is \( 6i \). Similarly, for any negative number, its square root can be represented in the form of a complex number.
| Radicand | Square Root |
|---|---|
| -40 | \( \pm 6.324i \) |
| -39 | \( \pm 6.245i \) |
| -38 | \( \pm 6.164i \) |
| -37 | \( \pm 6.083i \) |
| -36 | \( \pm 6i \) |
| -35 | \( \pm 5.916i \) |
| -34 | \( \pm 5.831i \) |
Applications and Examples
The concept of square roots of negative numbers extends beyond theoretical mathematics and finds applications in various fields. Below are some of the key applications and examples:
1. Electrical Engineering
In electrical engineering, complex numbers (which include imaginary numbers) are used to analyze and design circuits. The square root of negative numbers helps in calculating impedance, which is crucial for understanding the behavior of AC (alternating current) circuits.
- Example: Impedance in an AC circuit can be represented as \( Z = R + jX \), where \( j \) is the imaginary unit \( \sqrt{-1} \). If the reactance \( X \) is a negative value, it indicates capacitive reactance.
2. Control Systems
In control systems, complex numbers are used to describe the behavior of dynamic systems. The square roots of negative numbers are used in the calculation of the system poles and zeros, which determine the stability and response of the system.
- Example: The characteristic equation of a control system may have roots like \( -3 \pm 4i \), indicating oscillatory components in the system's response.
3. Quantum Mechanics
Quantum mechanics extensively uses complex numbers to describe wave functions and probability amplitudes. The square root of negative numbers is essential in solving Schrödinger's equation, which describes how quantum states evolve over time.
- Example: The wave function \( \psi(x, t) \) often contains complex exponentials, such as \( e^{i(kx - \omega t)} \), where \( i \) is the imaginary unit.
4. Signal Processing
In signal processing, complex numbers are used to represent and manipulate signals. The Fourier transform, which converts a signal from the time domain to the frequency domain, involves the use of imaginary numbers.
- Example: The Fourier transform of a time-domain signal \( f(t) \) is given by \( F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} dt \), where \( i \) is the imaginary unit.
Example Calculation: Square Root of -36
To find the square root of -36, we use the imaginary unit \( i \), where \( i = \sqrt{-1} \).
Step-by-step calculation:
- Rewrite -36 as \( -1 \times 36 \).
- Separate the square roots: \( \sqrt{-36} = \sqrt{-1 \times 36} = \sqrt{-1} \times \sqrt{36} \).
- Use \( i = \sqrt{-1} \) and \( \sqrt{36} = 6 \): \( \sqrt{-36} = i \times 6 = 6i \).
Thus, the square root of -36 is \( 6i \).
Square Root Table
The square root table below provides the square roots of some negative numbers, including -36. Each entry in the table shows the negative number (radicand) and its corresponding imaginary square root value.
| Radicand | Square Root |
|---|---|
| -40 | \(\pm 6.3245553203i\) |
| -39 | \(\pm 6.2449979984i\) |
| -38 | \(\pm 6.1644140030i\) |
| -37 | \(\pm 6.0827625303i\) |
| -36 | \(\pm 6i\) |
| -35 | \(\pm 5.9160797831i\) |
| -34 | \(\pm 5.8309518948i\) |
| -33 | \(\pm 5.7445626465i\) |
| -32 | \(\pm 5.6568542495i\) |
This table demonstrates how the square roots of negative numbers are always imaginary, represented with the imaginary unit \(i\). For instance, the square root of -36 is \( \pm 6i \), indicating that when \(6i\) is squared, it results in -36.

Frequently Asked Questions
-
What is the square root of -36?
The square root of -36 is \(6i\). This is because the square root of a negative number involves the imaginary unit \(i\), where \(i = \sqrt{-1}\). Therefore, \(\sqrt{-36} = \sqrt{36} \cdot \sqrt{-1} = 6i\).
-
What is an imaginary number?
An imaginary number is a number that can be written as a real number multiplied by the imaginary unit \(i\), where \(i = \sqrt{-1}\). Imaginary numbers are used to extend the concept of the square root to negative numbers.
-
How do you calculate the square root of a negative number?
To calculate the square root of a negative number, you first factor out the negative sign using the imaginary unit \(i\). For example, \(\sqrt{-x} = \sqrt{x} \cdot i\). This method allows you to work with negative numbers under the square root by converting them to imaginary numbers.
-
Why is the square root of -36 not a real number?
The square root of -36 is not a real number because the square root of a negative number does not exist within the set of real numbers. Instead, it exists in the set of complex numbers, which includes imaginary numbers.
-
What are some applications of imaginary numbers?
Imaginary numbers are used in various fields such as electrical engineering, quantum physics, applied mathematics, and control theory. They are essential for solving certain equations and modeling real-world phenomena that cannot be represented using only real numbers.
-
Can imaginary numbers be added and multiplied like real numbers?
Yes, imaginary numbers can be added, subtracted, multiplied, and divided using specific rules. For instance, when multiplying two imaginary numbers, you apply the rule \(i \cdot i = -1\). This helps in simplifying complex number operations.
-
Are there any visual representations of imaginary numbers?
Imaginary numbers can be represented on the complex plane, where the horizontal axis represents real numbers and the vertical axis represents imaginary numbers. This helps in visualizing operations involving complex numbers.
Khám phá căn bậc hai của -36. Video giải thích chi tiết về căn bậc hai của số âm và các khái niệm liên quan.
Căn bậc hai của -36 | Root(-36) | Căn bậc hai của số âm 36
READ MORE:
Hướng dẫn cách đơn giản hóa căn bậc hai âm. Video giải thích chi tiết về cách tìm và đơn giản hóa căn bậc hai của số âm 36.
Cách đơn giản hóa căn bậc hai âm −√36