Topic is the square root of 2 irrational: Is the square root of 2 irrational? This intriguing question has fascinated mathematicians for centuries. In this article, we delve into the mathematical proof, explore the historical context, and uncover why the square root of 2 is indeed an irrational number. Join us on this enlightening journey through the world of numbers.
Table of Content
Is the Square Root of 2 Irrational?
The question of whether the square root of 2 is irrational has been a topic of mathematical inquiry for centuries. Here is a detailed explanation:
Definition of Irrational Numbers
An irrational number is a real number that cannot be expressed as a ratio of two integers. In other words, it cannot be written in the form , where and are integers and .
Proof of the Irrationality of the Square Root of 2
The most common proof of the irrationality of is by contradiction. Here is a step-by-step explanation:
- Assume that is rational. Then it can be written as , where and are coprime integers (i.e., their greatest common divisor is 1).
- Then, , which simplifies to .
- Multiplying both sides by gives .
- This implies that is even, since it is equal to (a multiple of 2).
- If is even, then must also be even (since the square of an odd number is odd).
- Therefore, let for some integer .
- Substituting into the equation gives , which simplifies to or .
- This implies that is also even, and therefore must be even.
- Since both and are even, they have a common factor of 2. This contradicts our initial assumption that and are coprime.
Since our initial assumption leads to a contradiction, it follows that cannot be expressed as a ratio of two integers. Therefore, is irrational.

READ MORE:
Introduction
The question of whether the square root of 2 is irrational is a fundamental topic in mathematics that has intrigued scholars for centuries. An irrational number is a real number that cannot be expressed as a simple fraction, meaning it cannot be written in the form , where and are integers with .
Understanding why the square root of 2 is irrational involves delving into mathematical proofs and the historical context of this discovery. The most well-known proof of its irrationality is by contradiction, demonstrating that no fraction can accurately represent . This insight not only highlights the complexity of numbers but also the elegance of mathematical reasoning.
In this article, we will explore the definition of rational and irrational numbers, the historical background of the problem, and the detailed proof by contradiction. We will also touch upon the geometric interpretation of and its applications in various fields. This comprehensive overview aims to provide a clear and thorough understanding of why the square root of 2 is classified as an irrational number.
Definition of Rational and Irrational Numbers
To understand why the square root of 2 is irrational, it is essential to first define what rational and irrational numbers are. These two categories encompass all real numbers and are fundamental to number theory.
Rational Numbers: A rational number is any number that can be expressed as a fraction of two integers, where the numerator is an integer \( p \) and the denominator is a non-zero integer \( q \). In mathematical terms, a rational number can be written as:
Examples of rational numbers include:
- (0.5)
- (-0.75)
- 5 (since it can be written as )
Irrational Numbers: An irrational number, on the other hand, cannot be expressed as a fraction of two integers. This means there are no integers \( p \) and \( q \) such that the number can be written as . Irrational numbers have non-repeating, non-terminating decimal expansions.
Examples of irrational numbers include:
- (approximately 3.14159...)
- (approximately 2.71828...)
- (approximately 1.41421...)
The distinction between rational and irrational numbers is crucial for understanding many concepts in mathematics, including the proof that demonstrates the irrationality of the square root of 2. Rational numbers represent quantities that can be precisely divided into equal parts, while irrational numbers represent quantities that cannot be perfectly expressed as a simple fraction.
Historical Context
The discovery of the irrationality of the square root of 2 is a significant milestone in the history of mathematics. This discovery dates back to ancient Greece and is often attributed to the Pythagoreans, a group of mathematicians and philosophers led by Pythagoras.
The Pythagoreans believed that all numbers could be expressed as the ratio of two integers, a concept that aligned with their philosophical views of harmony and order in the universe. However, the discovery of irrational numbers challenged this belief and led to a profound shift in mathematical understanding.
According to historical accounts, the discovery of the irrationality of is credited to Hippasus, a member of the Pythagorean school. He demonstrated that the diagonal of a square with side length 1 cannot be expressed as a ratio of two integers, contradicting the Pythagorean doctrine. This diagonal is, in fact, the square root of 2.
The proof by contradiction, which showed that no fraction could represent , was revolutionary. This discovery reportedly caused significant discord among the Pythagoreans, as it undermined their foundational beliefs. Some legends suggest that Hippasus faced severe consequences for revealing this truth, although the historical accuracy of these stories is debated.
The impact of this discovery extended beyond the Pythagorean school. It paved the way for the acceptance and study of irrational numbers in mathematics. Over time, mathematicians developed a deeper understanding of these numbers, leading to advancements in various fields, including algebra, calculus, and number theory.
The historical context of the square root of 2's irrationality highlights the evolution of mathematical thought and the importance of challenging established beliefs. It serves as a reminder of the ever-expanding nature of mathematical knowledge and the quest for understanding the complexities of numbers.
Mathematical Proofs of Irrationality
The proof that the square root of 2 is irrational is a cornerstone in mathematics. This proof can be approached in several ways, each demonstrating that cannot be expressed as a ratio of two integers. The most well-known and widely taught method is proof by contradiction.
Proof by Contradiction
The proof by contradiction involves assuming the opposite of what we want to prove, and then showing that this assumption leads to a logical inconsistency. Here’s the step-by-step proof:
- Assume that is rational. This means it can be written as a fraction , where and are coprime integers (i.e., their greatest common divisor is 1).
- By squaring both sides, we get: , which simplifies to .
- Multiplying both sides by results in: .
- This implies that is even, because it is equal to (an even number).
- If is even, then must also be even (since the square of an odd number is odd). Let for some integer .
- Substituting into the equation gives: , which simplifies to or .
- This implies that is also even, and therefore must be even.
- Since both and are even, they have a common factor of 2. This contradicts our initial assumption that and are coprime.
Since our initial assumption leads to a contradiction, it follows that cannot be expressed as a ratio of two integers, and thus is irrational.
Geometric Proof
Another approach to proving the irrationality of involves geometric arguments, particularly related to the properties of right triangles.
- Consider an isosceles right triangle with legs of length 1. By the Pythagorean theorem, the length of the hypotenuse is .
- If were rational, it could be expressed as a fraction in simplest form.
- By scaling the triangle such that the hypotenuse and legs are integers, we again encounter the same contradiction as in the algebraic proof.
These proofs not only establish the irrationality of but also highlight the power and elegance of mathematical reasoning. The discovery and understanding of irrational numbers have profound implications in various fields of mathematics and beyond.

Proof by Contradiction
The proof that the square root of 2 is irrational can be established through a classic method known as proof by contradiction.
Assume, for contradiction, that √2 is rational. This means it can be expressed as a fraction in its simplest form, where a and b are integers, and b ≠ 0:
√2 = a/b
Squaring both sides gives:
2 = a² / b²
Multiplying both sides by b² yields:
2b² = a²
From this equation, we deduce that a² must be even, since it is equal to 2 times b². Therefore, a itself must be even.
Let's rewrite a in terms of an integer k:
a = 2k
Substituting back into our equation:
2b² = (2k)²
2b² = 4k²
Dividing both sides by 2 gives:
b² = 2k²
Now, we see that b² is also even, implying that b must also be even.
However, if both a and b are even, then the fraction a/b is not in its simplest form, as both a and b share a common factor of 2.
This contradicts our initial assumption that √2 can be expressed as a fraction in its simplest form, thereby proving that √2 cannot be rational.
Hence, we conclude that the square root of 2 is irrational.
Geometric Interpretation
The square root of 2 can be understood geometrically by considering the diagonal of a square. Let's explore this in detail:
- Imagine a square with each side of length 1 unit.
- The diagonal of this square cuts it into two right-angled triangles.
- Using the Pythagorean theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides, we can find the length of the diagonal.
Here is how the calculation works:
- Each side of the square is 1 unit, so we apply the Pythagorean theorem:
- In this case, , and is the diagonal.
- Substituting the values, we get:
- This simplifies to:
- Taking the square root of both sides, we find:
Therefore, the length of the diagonal is the square root of 2. Geometrically, this length cannot be expressed as a ratio of two integers, which is why the square root of 2 is considered an irrational number.
To visualize this further, consider trying to measure the diagonal using a ruler marked with rational numbers (fractions). No matter how finely you divide the ruler, you will never be able to exactly measure the diagonal, illustrating its irrational nature.
Applications of Irrational Numbers
Irrational numbers, like the square root of 2, have significant applications in various fields of science, engineering, and mathematics. Here are some notable examples:
- Geometry and Trigonometry:
The square root of 2 plays a crucial role in geometry, particularly in the properties of right-angled triangles. For instance, in an isosceles right triangle, the length of the hypotenuse is the square root of 2 times the length of each leg. This relationship is fundamental in trigonometry, where it helps in solving problems involving right-angled triangles.
- Engineering and Architecture:
Architects and engineers often use the square root of 2 in designing structures. The ancient Romans employed a technique called "ad quadratum" which utilized the diagonal of a square (equal to the square root of 2 times the side length) to double the area of squares, aiding in the construction of buildings and pavements.
- Physics:
In physics, irrational numbers like the square root of 2 appear in various equations and constants. For example, the square root of 2 is important in calculations involving wave functions and quantum mechanics.
- Mathematical Theorems and Proofs:
The discovery of irrational numbers was a turning point in the history of mathematics. It led to the development of real number theory and rigorous proofs. The proof of the irrationality of the square root of 2 is often one of the first examples of a proof by contradiction taught in mathematics.
- Computer Science:
Irrational numbers are essential in computer algorithms that require high precision calculations. The square root of 2 is used in algorithms for numerical approximations and simulations.
- Music Theory:
In music, the square root of 2 is related to the concept of equal temperament tuning, where an octave is divided into twelve equal parts. This tuning system ensures that music sounds harmonious regardless of the key it is played in.
These applications highlight the importance and ubiquity of irrational numbers in both theoretical and practical contexts.
Square Root of 2 in Various Fields
The square root of 2, often denoted as \( \sqrt{2} \), is a significant mathematical constant with numerous applications across various fields. Here, we explore its relevance in different areas:
Geometry and Architecture
In geometry, \( \sqrt{2} \) arises when calculating the diagonal of a square. For a square with side length 1, the diagonal is \( \sqrt{2} \). This relationship is foundational in the Pythagorean theorem, where the square root of the sum of the squares of the sides of a right triangle gives the length of the hypotenuse.
In ancient Roman architecture, the square root of 2 was used in the "ad quadratum" technique to design structures. This method involves creating a square whose diagonal is used as the side length of a new square, effectively doubling the area of the original square.
Physics and Engineering
In physics, \( \sqrt{2} \) appears in various formulas and calculations, particularly in wave mechanics and quantum physics. For example, in the analysis of wave interference patterns, the path difference between waves that leads to constructive or destructive interference often involves the square root of 2.
In engineering, particularly in electrical engineering, \( \sqrt{2} \) is essential in calculating the RMS (root mean square) values of alternating current (AC) voltages and currents. The RMS value of a sine wave is the peak value divided by \( \sqrt{2} \), which is crucial for accurate power measurements.
Computer Science
Computer algorithms for graphics and design frequently use \( \sqrt{2} \). For instance, when calculating the distance between two points on a grid, the Euclidean distance formula incorporates \( \sqrt{2} \) for diagonal distances. Additionally, many algorithms for image processing and pixel interpolation depend on accurate calculations involving \( \sqrt{2} \).
Art and Design
The aesthetic appeal of the square root of 2 is evident in art and design. The aspect ratio of the paper sizes in the ISO 216 standard (such as A4 paper) is based on the ratio 1:\( \sqrt{2} \). This ratio allows for a sheet to be folded in half while maintaining the same aspect ratio, which is both practical and visually pleasing.
Mathematics
In mathematics, \( \sqrt{2} \) is a classic example of an irrational number, meaning it cannot be expressed as a simple fraction. This was a significant discovery in ancient Greek mathematics and remains a fundamental concept in number theory. The irrationality of \( \sqrt{2} \) can be proven using various methods, including proof by contradiction.
Overall, the square root of 2 is a vital constant with diverse applications, illustrating the interconnectedness of mathematics with the real world.
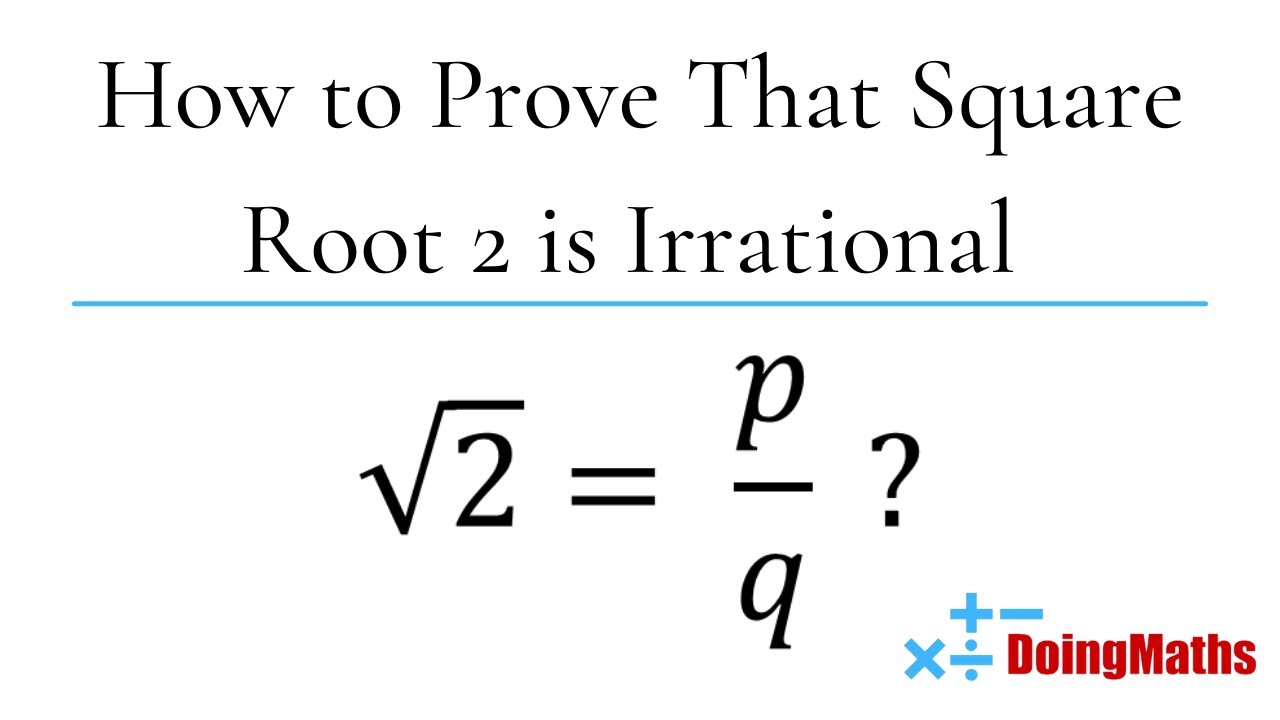
Common Misconceptions
Despite the well-established proof that the square root of 2 is irrational, there are several common misconceptions about this topic. Here, we will address and clarify these misunderstandings:
-
Misconception: Rational Approximation Implies Rationality
Some people believe that because the square root of 2 can be approximated by rational numbers, it must itself be rational. While it is true that we can find fractions like 1.414 or 1.41421356 that come close to the square root of 2, these are merely approximations and not exact values. No matter how many decimal places you use, these approximations will never exactly equal the square root of 2.
-
Misconception: All Roots of Whole Numbers are Rational
Another misconception is the assumption that the square root of any whole number must be rational. This is not true. While the square roots of perfect squares (e.g., 1, 4, 9, 16) are rational, the square roots of other numbers, such as 2, 3, or 5, are irrational.
-
Misconception: Proofs of Irrationality Are Incorrect or Incomplete
Some people doubt the proofs of the irrationality of the square root of 2, thinking they are flawed or incomplete. However, the classic proof by contradiction, attributed to Euclid, is robust and has been widely accepted by mathematicians for centuries. This proof shows that assuming the square root of 2 is rational leads to a logical contradiction, thereby proving its irrationality.
-
Misconception: Irrational Numbers Can Be Expressed as Long Fractions
There is a belief that if a number can be written as a very long fraction, it might be rational. However, irrational numbers cannot be expressed as any fraction of integers, regardless of how long or complex the fraction is. They have non-repeating, non-terminating decimal expansions.
Understanding these misconceptions helps clarify why the square root of 2 is classified as an irrational number and dispels common myths surrounding irrational numbers.
Conclusion
The irrationality of the square root of 2 is a significant discovery in mathematics, demonstrating that not all numbers can be expressed as simple fractions. This revelation has profound implications in various fields, from geometry to number theory, highlighting the richness and complexity of the number system.
Throughout history, the proof of the irrationality of √2 has been approached through different methods, with the most famous being the proof by contradiction. This method shows that assuming √2 is rational leads to a logical contradiction, thereby proving it must be irrational.
Understanding irrational numbers like √2 allows mathematicians to explore the limits of rational number representations and to appreciate the diversity of mathematical constants. The irrational nature of √2 also emphasizes the importance of precision and rigor in mathematical proofs and the necessity of careful reasoning in the study of mathematics.
In conclusion, the irrationality of √2 is a cornerstone of mathematical theory, demonstrating the deep and often surprising properties of numbers. This concept continues to inspire and challenge mathematicians, offering insights into the structure and behavior of the mathematical universe.
Bằng chứng rằng căn bậc hai của 2 là số vô tỉ | Đại số I | Khan Academy
READ MORE:
Bằng chứng: Căn bậc hai của 2 là vô tỉ