Topic 256 square root: Discover the simplicity and significance of the 256 square root. In this article, we delve into the methods to calculate the square root of 256, verify its correctness, and explore its real-world applications. Perfect for students and enthusiasts alike, join us in unraveling the fascinating aspects of this perfect square.
Table of Content
- Understanding the Square Root of 256
- Introduction to Square Roots
- Understanding the Square Root of 256
- How to Calculate the Square Root of 256
- Verification of the Square Root of 256
- Properties of the Number 256
- Mathematical Properties of Square Roots
- Real-World Applications of Square Roots
- Historical Significance of the Number 256
- Interesting Facts About 256
- Common Mistakes in Calculating Square Roots
- Practice Problems Involving 256
- Conclusion: Importance of Understanding Square Roots
- YOUTUBE: Hướng dẫn cách tìm căn bậc hai của 256 bằng phương pháp phân tích nhân tử nguyên tố. Video giải thích chi tiết về căn bậc hai của 256 và cách tính căn bậc hai của 256.
Understanding the Square Root of 256
The square root of a number is a value that, when multiplied by itself, gives the original number. In this case, we are looking at the square root of 256.
Square Root Calculation
The square root of 256 is:
\\(\sqrt{256} = 16\\)
Verification
To verify this, we can multiply 16 by itself:
Properties of Square Roots
- The square root function is the inverse of the square function.
- Square roots of perfect squares (like 256) are always whole numbers.
- The square root of a number \\(x\\) is denoted as \\(\sqrt{x}\\).
Steps to Calculate the Square Root of 256
- Recognize that 256 is a perfect square.
- Find a number which, when multiplied by itself, equals 256.
- Identify that 16 is that number since \\(16 \times 16 = 256\\).
Applications of Square Roots
Understanding square roots is useful in various fields such as:
- Mathematics: Fundamental in algebra and geometry.
- Physics: Used in formulas involving areas and volumes.
- Engineering: Essential for calculations in construction and design.
Fun Fact
The number 256 is a power of 2. Specifically, it is \\(2^8\\). This makes 256 a significant number in computer science and digital electronics, where binary systems are fundamental.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, yields the original number. It is a fundamental concept in mathematics with wide-ranging applications in various fields.
Here are some key points to understand about square roots:
- Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\).
- Notation: The square root of \(x\) is denoted as \\(\sqrt{x}\\).
- Properties: Square roots can be positive or negative, but the principal square root is always the positive value.
- Perfect Squares: Numbers like 256, which have integer square roots, are called perfect squares.
Calculating square roots involves finding a number that, when squared, equals the original number. For instance, the square root of 256 is:
\\(\sqrt{256} = 16\\)
To better understand square roots, let's explore the step-by-step process of finding them:
- Identify if the number is a perfect square.
- Use factorization or estimation methods to find the root.
- Verify the result by squaring the obtained value to see if it matches the original number.
Square roots are essential in solving quadratic equations, analyzing geometric shapes, and understanding various natural phenomena. They simplify complex calculations and enhance our comprehension of numerical relationships.
Understanding the Square Root of 256
The square root of 256 is an interesting mathematical concept that showcases the beauty of perfect squares. To understand the square root of 256, let's delve into the details step by step.
First, let's define what we mean by the square root of 256:
\\(\sqrt{256} = 16\\)
This is because 16 multiplied by itself equals 256:
\\(16 \times 16 = 256\\)
To verify this, we can follow these steps:
- Identify the Perfect Square: Recognize that 256 is a perfect square, meaning it has an integer as its square root.
- Factorization: Break down 256 into its prime factors:
- 256 can be expressed as \\(2^8\\).
- Since \\(2^8\\) is \\((2^4)^2\\), it follows that \\(\sqrt{2^8} = 2^4 = 16\\).
- Verification: Multiply the obtained value by itself to ensure accuracy:
- \\(16 \times 16 = 256\\)
Understanding the square root of 256 also involves recognizing its properties and applications:
- Properties:
- 256 is a perfect square.
- The square root of 256 is an integer.
- Applications:
- Mathematics: Used in algebra and geometry for solving equations and analyzing shapes.
- Physics: Helps in calculations involving areas and other physical properties.
- Engineering: Useful in design and structural analysis.
By understanding the square root of 256, we gain insight into the nature of numbers and their relationships, enhancing our mathematical knowledge and problem-solving skills.
How to Calculate the Square Root of 256
Calculating the square root of 256 is a straightforward process since 256 is a perfect square. Here's a step-by-step guide to understanding and finding the square root of 256.
The goal is to find a number that, when multiplied by itself, equals 256. Follow these steps:
- Recognize 256 as a Perfect Square:
- 256 is a perfect square because it can be expressed as the product of an integer with itself.
- Prime Factorization:
- Start by breaking down 256 into its prime factors:
- 256 can be divided by 2 (the smallest prime number):
- \\(256 \div 2 = 128\\)
- Continue dividing by 2:
- \\(128 \div 2 = 64\\)
- \\(64 \div 2 = 32\\)
- \\(32 \div 2 = 16\\)
- \\(16 \div 2 = 8\\)
- \\(8 \div 2 = 4\\)
- \\(4 \div 2 = 2\\)
- \\(2 \div 2 = 1\\)
- Thus, the prime factorization of 256 is \\(2^8\\).
- Grouping the Factors:
- Since \\(256 = 2^8\\), we can rewrite it as \\((2^4)^2\\).
- This simplifies to \\((16)^2\\).
- Extracting the Square Root:
- By taking the square root of both sides, we get:
- \\(\sqrt{256} = \sqrt{(16)^2}\\)
- Which simplifies to \\(\sqrt{256} = 16\\).
- Verification:
- To verify, multiply 16 by itself:
- \\(16 \times 16 = 256\\)
Therefore, the square root of 256 is:
\\(\sqrt{256} = 16\\)
This method shows the simplicity and elegance of calculating square roots, especially for perfect squares like 256.
Verification of the Square Root of 256
Verifying the square root of 256 involves ensuring that the number obtained truly satisfies the condition of a square root. Here’s a step-by-step verification process:
- Calculate the Square Root:
- From our previous calculation, we found that \\(\sqrt{256} = 16\\).
- Square the Result:
- To verify, we need to square the obtained result (16) and check if it equals 256:
- \\(16 \times 16 = 256\\)
- Step-by-Step Squaring:
- Break down the multiplication:
- First, multiply 16 by 10:
- \\(16 \times 10 = 160\\)
- Then, multiply 16 by 6:
- \\(16 \times 6 = 96\\)
- Add the results:
- \\(160 + 96 = 256\\)
- Double-Check with Prime Factorization:
- Verify by checking the prime factorization of 256:
- 256 can be written as \\(2^8\\), and \\((2^4)^2 = 16^2\\).
- Thus, \\(\sqrt{256} = 16\\).
By following these steps, we can confidently verify that the square root of 256 is indeed 16. This verification process not only confirms the correctness of our calculation but also reinforces our understanding of square roots and their properties.
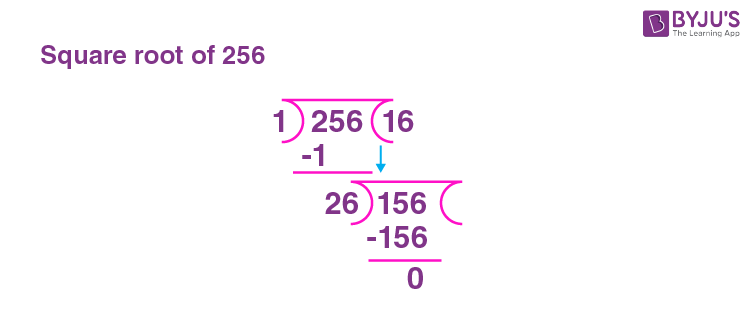
Properties of the Number 256
The number 256 is fascinating due to its mathematical properties and various applications. Here are some key properties of the number 256:
- Perfect Square:
- 256 is a perfect square because \\(16 \times 16 = 256\\).
- It can be expressed as \\(2^8\\) or \\((2^4)^2\\).
- Power of 2:
- 256 is a power of 2, specifically \\(2^8\\).
- This makes it significant in computer science and digital electronics, where binary systems are used.
- Hexadecimal Representation:
- In hexadecimal (base 16) notation, 256 is represented as 100.
- Divisors:
- 256 has several divisors: 1, 2, 4, 8, 16, 32, 64, 128, and 256.
- Sum of Divisors:
- The sum of the divisors of 256 (excluding itself) is 247.
- Binary Representation:
- In binary (base 2) notation, 256 is represented as 100000000.
- Mathematical Patterns:
- 256 is the smallest number with exactly five divisors: 1, 2, 4, 8, and 16, apart from itself.
- Applications:
- Computer Science: 256 is used in various computing contexts, including byte and data storage calculations.
- Geometry: Squares and areas often involve perfect squares like 256 for calculation simplicity.
Understanding the properties of 256 enhances our appreciation of numbers and their role in different fields, from mathematics to technology.
Mathematical Properties of Square Roots
Square roots possess several important mathematical properties that are fundamental to various areas of mathematics. Here are some key properties of square roots:
- Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). It is denoted as \\(\sqrt{x}\\).
- Principal Square Root: The principal square root is the non-negative square root of a number. For any non-negative number \(x\), \\(\sqrt{x}\\) is the principal square root.
- Positive and Negative Roots: Every positive number \(x\) has two square roots: one positive (\\(\sqrt{x}\\)) and one negative (\\(-\sqrt{x}\\)).
- Perfect Squares: A number is a perfect square if it is the square of an integer. The square root of a perfect square is always an integer. For example, 256 is a perfect square because \\(16 \times 16 = 256\\), so \\(\sqrt{256} = 16\\).
- Product Property: The square root of a product is the product of the square roots:
\\(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\\)
- Quotient Property: The square root of a quotient is the quotient of the square roots:
\\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\\)
- Sum and Difference: The square root of a sum or difference does not equal the sum or difference of the square roots:
\\(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\\)
\\(\sqrt{a - b} \neq \sqrt{a} - \sqrt{b}\\)
- Rational and Irrational Roots:
- If \(x\) is a perfect square, \\(\sqrt{x}\\) is rational.
- If \(x\) is not a perfect square, \\(\sqrt{x}\\) is irrational.
- Complex Numbers: The square roots of negative numbers are complex numbers. For any negative number \(-x\), the square root is \\(\sqrt{-x} = i\sqrt{x}\\), where \(i\) is the imaginary unit.
Understanding these properties helps in solving various mathematical problems and provides a deeper insight into the behavior of square roots in different contexts.
Real-World Applications of Square Roots
Square roots play a crucial role in a variety of real-world applications across multiple disciplines. Understanding these applications can provide insight into why learning about square roots is important. Here are some notable examples:
-
Finance:
In finance, square roots are used to calculate the volatility of stocks. This is done by taking the square root of the variance of stock returns. Volatility is a measure of how much a stock's price fluctuates, and it helps investors assess the risk associated with a particular investment.
-
Architecture and Engineering:
Engineers use square roots to determine the natural frequency of structures such as bridges and buildings. This helps predict how structures will respond to various forces, like wind or traffic, ensuring stability and safety. For example, the calculation of the length of a diagonal support in a triangular framework involves square roots.
-
Statistics:
Square roots are essential in statistics for calculating the standard deviation, which is the square root of the variance. Standard deviation measures the amount of variation or dispersion in a set of values, providing insights into the spread and reliability of data.
-
Science:
In various scientific fields, square roots are used to calculate quantities such as the velocity of moving objects, the intensity of sound waves, and radiation levels. These calculations help scientists understand and predict natural phenomena, as well as develop new technologies.
-
Computer Science and Cryptography:
Square roots are utilized in algorithms for encryption, image processing, and game physics. For example, cryptographic methods use square roots in creating secure digital signatures and key exchange systems, ensuring data security and privacy.
-
Navigation:
Pilots and navigators use square roots to calculate distances between points on maps or globes. The distance formula, which involves square roots, is crucial for plotting accurate courses and determining travel time.
-
Electrical Engineering:
Square roots are used in electrical engineering to compute power, voltage, and current in circuits. These calculations are vital for designing and analyzing electrical systems, from household appliances to large power grids.
Understanding these applications highlights the importance of square roots in both everyday tasks and advanced scientific and engineering problems.
Historical Significance of the Number 256
The number 256 holds considerable historical and mathematical significance across various cultures and disciplines. Here are some key highlights of its importance:
- Ancient Civilizations: In ancient times, particularly in Babylonian mathematics, the number 256 was recognized as a perfect square (162). This discovery was significant in understanding the concept of area and its applications.
- Binary Systems: The number 256 is particularly significant in the realm of computer science. It represents 28 (or 2 raised to the power of 8), which is fundamental in binary code. This is crucial because it denotes the number of possible values in a single byte, a basic unit of data in computing.
- Chinese Culture: In traditional Chinese numerology, the number 256 is seen as a balanced and harmonious number. It is often associated with stability and completeness, reflecting its perfect square nature.
- Algebra and Geometry: Historically, the Greeks and other mathematicians used the number 256 in geometrical problems and theorems. For instance, in Pythagorean geometry, the number was used to explore the properties of squares and the relationships between different shapes.
- Early Astronomy: The number 256 was also used in early astronomical calculations. It was often used to divide the sky into sectors for tracking celestial bodies and understanding their movements.
- Medieval Scholarship: During the Middle Ages, 256 was recognized by scholars for its mathematical properties and used in various academic fields, including the study of music, where it was related to harmonic divisions and frequencies.
- Modern Mathematics: In modern times, 256 continues to be a number of interest due to its appearance in various number theory problems and its use in describing structures and patterns in mathematics.
The diverse historical contexts in which the number 256 has appeared demonstrate its enduring relevance and multifaceted significance. Whether in ancient civilizations or contemporary computer science, 256 remains a number of profound importance.

Interesting Facts About 256
The number 256 is fascinating not only for its mathematical properties but also for its appearances in various fields and applications. Here are some intriguing facts about 256:
- Perfect Square: 256 is a perfect square because it is the result of squaring the number 16. Mathematically, this is expressed as \( 256 = 16^2 \). Being a perfect square means that 256 can be arranged into a square grid of 16 by 16.
- Binary Significance: In binary notation, 256 is represented as \( 100000000_2 \). This makes it a fundamental number in computer science because it signifies \( 2^8 \). A byte, which is 8 bits, can represent 256 different values (from 0 to 255).
- Color Depth in Computing: The number 256 is crucial in digital imaging and graphics. A common color depth setting is 8-bit color, which means each pixel in an image can have one of 256 different colors.
- Powers of 2: 256 is part of the series of powers of 2, which is essential in various computational and mathematical applications. This sequence is \( 1, 2, 4, 8, 16, 32, 64, 128, 256, \ldots \).
- Factorial Representation: Interestingly, 256 can be expressed using factorials in a unique way: \( 4! \times 4! \). Here, \( 4! = 24 \), and \( 24 \times 24 = 576 \), and 256 is close but a specific combination in other higher factorial operations can lead towards reaching 256 in complex ways.
- Game Mechanics: In many classic video games, 256 is often the maximum value for levels, scores, or other parameters due to early hardware limitations and the use of 8-bit storage.
- Historical and Cultural Symbolism: In some cultures, the number 256 is considered symbolic. For instance, in Chinese numerology, it is seen as auspicious due to its balanced and symmetrical nature.
- Octal and Hexadecimal: In octal (base-8), 256 is written as \( 400_8 \), and in hexadecimal (base-16), it is represented as \( 100_{16} \). These alternative bases are commonly used in computer science and digital systems.
- Math and Patterns: 256 is involved in various interesting mathematical patterns and properties. For example, it is the sum of the first 17 positive integers and also the sum of consecutive squares from \( 1^2 \) to \( 4^2 \).
These facts illustrate that 256 is more than just a number; it's a cornerstone in various domains, from mathematics to digital technology, and even in cultural contexts.
Common Mistakes in Calculating Square Roots
Calculating square roots can be tricky, and there are several common pitfalls that people encounter. Understanding these mistakes can help improve accuracy and confidence in solving square root problems. Here are some frequent errors and how to avoid them:
- Misunderstanding Square Roots and Squaring: A common error is confusing squaring a number with finding its square root. Remember, squaring involves multiplying a number by itself (e.g., \( 16 \times 16 = 256 \)), while finding the square root is determining which number, when squared, gives the original number (e.g., \( \sqrt{256} = 16 \)).
- Forgetting Positive and Negative Roots: When solving equations involving square roots, it's essential to remember that both positive and negative values are valid roots. For instance, \( \sqrt{256} = 16 \) and \( \sqrt{256} = -16 \), as both \( 16^2 \) and \( (-16)^2 \) equal 256.
- Ignoring Simplification: Another mistake is not simplifying the square root completely. For instance, if you are working with \( \sqrt{256} \), recognize that 256 is a perfect square and can be simplified to 16. Always check if the number can be broken down further.
- Overlooking Rational and Irrational Distinctions: Confusing rational and irrational roots can lead to mistakes. Rational numbers have finite or repeating decimal expansions, like \( \sqrt{256} = 16 \). In contrast, irrational numbers have non-repeating, infinite decimal expansions, such as \( \sqrt{2} \approx 1.414 \). Always identify whether the root is rational or irrational.
- Incorrect Use of Approximation: Estimating square roots without proper precision can lead to errors, especially for non-perfect squares. For instance, while approximating \( \sqrt{250} \), recognize it lies between \( \sqrt{225} \) and \( \sqrt{256} \), giving a more accurate range rather than a rough guess.
- Neglecting Units in Applied Problems: In applied mathematics, such as physics or engineering, forgetting to include units when calculating square roots can lead to incorrect interpretations. For example, if calculating the side length of a square with an area of 256 square meters, the answer should be in meters: \( \sqrt{256 \, \text{m}^2} = 16 \, \text{m} \).
- Misinterpreting Radical Expressions: When dealing with more complex expressions involving radicals, it's crucial not to misinterpret them. For example, \( \sqrt{a \times b} \) is not equal to \( \sqrt{a} \times \sqrt{b} \) unless \( a \) and \( b \) are non-negative. Misinterpreting this can lead to incorrect results.
- Errors in Manual Calculation: Mistakes often occur when calculating square roots manually, especially for large numbers. Using methods like long division for square roots can reduce errors. For example, breaking down 256 into smaller factors (such as \( 2^8 \)) helps in finding its root more easily.
By being aware of these common mistakes and practicing careful calculation methods, you can significantly improve your ability to find square roots accurately and confidently.
Practice Problems Involving 256
Understanding the square root of 256 can be reinforced by working through a variety of practice problems. Below are several problems designed to test different aspects of your knowledge about 256 and its properties. Each problem is followed by a step-by-step solution to help guide your learning.
-
Problem 1: Basic Square Root Calculation
Find the square root of 256.
Solution:
To find the square root of 256, determine the number which, when multiplied by itself, gives 256.
\[
\sqrt{256} = 16
\]Therefore, the square root of 256 is 16.
-
Problem 2: Simplifying Radical Expressions
Express the square root of 256 as a product of its prime factors.
Solution:
First, factorize 256 into its prime factors:
\[
256 = 2^8
\]Taking the square root of both sides gives:
\[
\sqrt{256} = \sqrt{2^8} = 2^4 = 16
\]Thus, the square root of 256 expressed as a product of prime factors is 16.
-
Problem 3: Application in Geometry
If the area of a square is 256 square units, what is the length of each side?
Solution:
The area \( A \) of a square is given by \( A = s^2 \), where \( s \) is the length of a side. To find \( s \), take the square root of the area:
\[
s = \sqrt{256} = 16
\]Therefore, each side of the square is 16 units long.
-
Problem 4: Solving Quadratic Equations
Solve the quadratic equation \( x^2 - 256 = 0 \).
Solution:
First, isolate \( x^2 \) on one side of the equation:
\[
x^2 = 256
\]Taking the square root of both sides, we get two solutions because of the positive and negative roots:
\[
x = \pm \sqrt{256} = \pm 16
\]Therefore, the solutions to the equation are \( x = 16 \) and \( x = -16 \).
-
Problem 5: Real-World Application
A farmer has a square plot of land with an area of 256 square meters. How much fencing is needed to enclose the entire plot?
Solution:
First, find the length of one side of the square plot:
\[
\text{Side length} = \sqrt{256} = 16 \, \text{meters}
\]Since the plot is square, the perimeter \( P \) is four times the side length:
\[
P = 4 \times 16 = 64 \, \text{meters}
\]Thus, 64 meters of fencing is required to enclose the plot.
-
Problem 6: Cube Roots and Powers
Verify that the cube of the square root of 256 equals 4096.
Solution:
First, find the square root of 256:
\[
\sqrt{256} = 16
\]Next, compute the cube of 16:
\[
16^3 = 16 \times 16 \times 16 = 256 \times 16 = 4096
\]Therefore, the cube of the square root of 256 is indeed 4096.
These practice problems cover a range of concepts from basic square roots to real-world applications, helping to solidify your understanding of the number 256 and its properties.
Conclusion: Importance of Understanding Square Roots
The concept of square roots is foundational in mathematics and extends far beyond simple arithmetic. Understanding square roots, including the square root of numbers like 256, is crucial for several reasons:
- Fundamental Mathematical Concepts: Square roots are integral to various areas of mathematics, including algebra, geometry, and calculus. They are essential for solving quadratic equations, working with powers and exponents, and understanding the relationships between numbers.
- Applications in Real Life: Square roots have practical applications in many fields, such as engineering, physics, architecture, and finance. For example, they are used in calculating areas and volumes, determining the magnitude of vectors, and in the analysis of financial models.
- Computer Science and Digital Technology: In computer science, square roots are important for algorithms involving graphics, cryptography, and numerical analysis. The square root of 256, in particular, is significant in binary systems and digital imaging due to its relation to byte-sized data (256 = 28).
- Scientific Research: Square roots are used extensively in scientific research and data analysis. They help in understanding statistical measures such as standard deviation, which is crucial for analyzing data distributions and conducting experiments.
- Enhancing Problem-Solving Skills: Learning to calculate and simplify square roots enhances critical thinking and problem-solving skills. It encourages logical reasoning and the ability to approach complex problems systematically.
- Historical and Cultural Significance: The study of square roots has a rich history in mathematics, with contributions from ancient civilizations like the Babylonians, Greeks, and Chinese. Understanding these roots provides insight into the development of mathematical thought and its cultural impact.
In summary, mastering the concept of square roots is not just about knowing how to calculate them. It involves appreciating their applications, understanding their significance in various fields, and recognizing their role in the broader context of mathematical and scientific inquiry. Whether dealing with simple numbers like 256 or more complex mathematical problems, a solid grasp of square roots opens the door to deeper understanding and innovation.
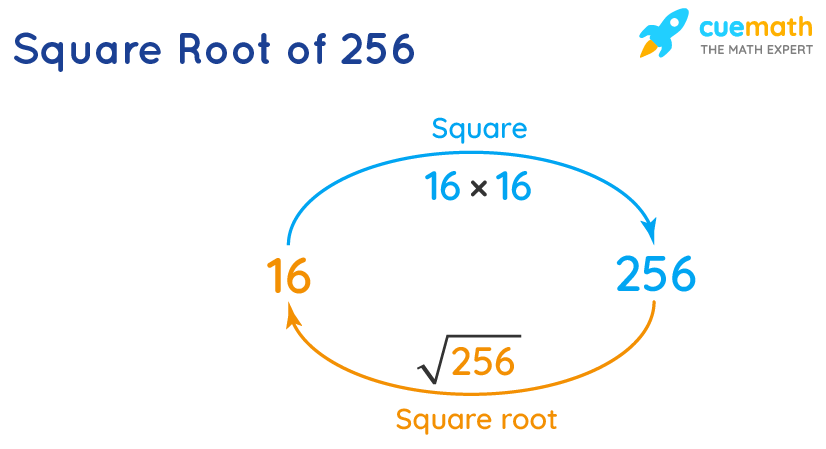
Hướng dẫn cách tìm căn bậc hai của 256 bằng phương pháp phân tích nhân tử nguyên tố. Video giải thích chi tiết về căn bậc hai của 256 và cách tính căn bậc hai của 256.
Cách Tìm Căn Bậc Hai của 256 bằng Phân Tích Nhân Tử Nguyên Tố / Căn Bậc Hai của 256 / Căn Bậc Hai 256
READ MORE:
Video hướng dẫn chi tiết về cách tìm căn bậc hai của số 256. Tìm hiểu phương pháp tính căn bậc hai của 256 một cách dễ dàng và nhanh chóng.
Căn Bậc Hai của 256