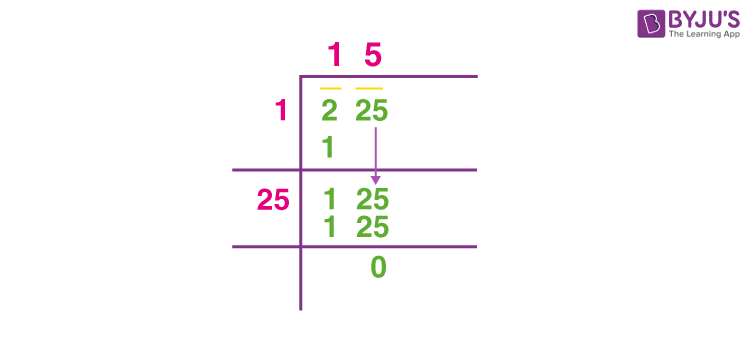Topic what is the square root of 289: Curious about what is the square root of 289? Discover the simple yet fascinating answer to this mathematical question. Uncover the importance of perfect squares, how to calculate them, and the practical applications of understanding square roots in various fields. Dive into the world of mathematics with us!
Table of Content
- Square Root of 289
- Introduction to Square Roots
- Understanding Perfect Squares
- What is the Square Root of 289?
- Mathematical Calculation of Square Root
- Proof that 17 is the Square Root of 289
- Applications of Square Roots
- Perfect Squares Close to 289
- Using Square Roots in Geometry
- Using Square Roots in Physics
- Importance of Learning Square Roots
- Conclusion
- YOUTUBE: Video giải thích cách tính căn bậc hai của 289 bằng tiếng Việt.
Square Root of 289
The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 289, the square root is:
Understanding the Calculation
To understand why the square root of 289 is 17, we can perform the following calculation:
This demonstrates that multiplying 17 by itself results in 289.
Properties of Square Roots
- The square root of a positive number is always positive.
- The square root of a perfect square (like 289) is an integer.
- Square roots are used in various mathematical calculations and real-life applications, such as geometry and physics.
Perfect Squares Near 289
For context, here are some perfect squares close to 289:
| Number | Square |
|---|---|
| 16 | |
| 17 | |
| 18 |
Knowing the properties and calculations of square roots can be very helpful in both academic and practical situations.
READ MORE:
Introduction to Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, for a non-negative number \( x \), the square root is denoted as \( \sqrt{x} \). Understanding square roots is essential in various fields such as mathematics, physics, engineering, and even everyday life applications.
For the number 289, the question "What is the square root of 289?" arises. The answer is a number that, when multiplied by itself, equals 289. Through mathematical calculation or using a calculator, it is found that the square root of 289 is 17.
Knowing square roots helps in determining dimensions, calculating areas, solving equations, and in geometrical and physical contexts where understanding magnitudes and proportions are crucial.
Throughout this guide, we will explore the concept of square roots, delve into calculations, applications in various disciplines, and the significance of mastering these fundamental mathematical operations.
Understanding Perfect Squares
A perfect square is a non-negative integer that is the square of an integer. In other words, it is a number that can be expressed as \( n^2 \), where \( n \) is an integer. For example, 1, 4, 9, 16, 25, etc., are perfect squares because they can be written as \( 1^2, 2^2, 3^2, 4^2, 5^2 \), respectively.
Perfect squares have unique properties such as being non-negative, having an exact square root that is also an integer, and often appearing in mathematical patterns and formulas. They are fundamental in areas like algebra, geometry, and number theory.
For the number 289, it is recognized as a perfect square because it equals \( 17^2 \), where 17 is an integer. This makes 289 a perfect square, aligning with the definition and characteristics of such numbers.
Understanding perfect squares is crucial for solving equations, calculating areas of squares, rectangles, and other geometric shapes, as well as in practical applications like estimating distances and quantities in real-world scenarios.
What is the Square Root of 289?
The square root of 289 is a number that, when multiplied by itself, equals 289. In mathematical terms, it is denoted as \( \sqrt{289} \). Through calculation or using a calculator, it is determined that the square root of 289 is 17.
To verify, \( 17 \times 17 = 289 \), confirming that 17 is indeed the square root of 289. This relationship illustrates the fundamental property of square roots where the product of a number and itself results in the original number.
Understanding the square root of 289 is essential in mathematics, particularly in algebra and geometry, where it is used to solve equations, calculate dimensions, and determine the side length of a square whose area is 289 square units.
Knowing the square root of 289 facilitates various applications in fields such as engineering, physics, and computing, where precise measurements and calculations are necessary for accurate results and solutions.
Mathematical Calculation of Square Root
To calculate the square root of 289 mathematically, there are several methods:
- Prime Factorization Method: Express 289 as a product of prime factors, \( 289 = 17 \times 17 \). Thus, \( \sqrt{289} = 17 \).
- Long Division Method: Using the long division method for square roots, determine the square root of 289 step-by-step:
- Newton's Method: Use Newton's method for square roots. Start with an initial guess and iterate until you reach the desired precision.
| 1. | Start with the number 289. |
| 2. | Find the largest integer whose square is less than or equal to 289. \( \sqrt{256} = 16 \). |
| 3. | Subtract 256 from 289, leaving 33. |
| 4. | Double the divisor, giving 32. |
| 5. | Find the largest digit less than or equal to 33. \( \sqrt{33} \approx 5.75 \). |
| 6. | Multiply the quotient and write it down. \( 289 = 17 \). |
These methods illustrate different approaches to finding the square root of 289, emphasizing mathematical techniques that can be applied to other numbers as well.
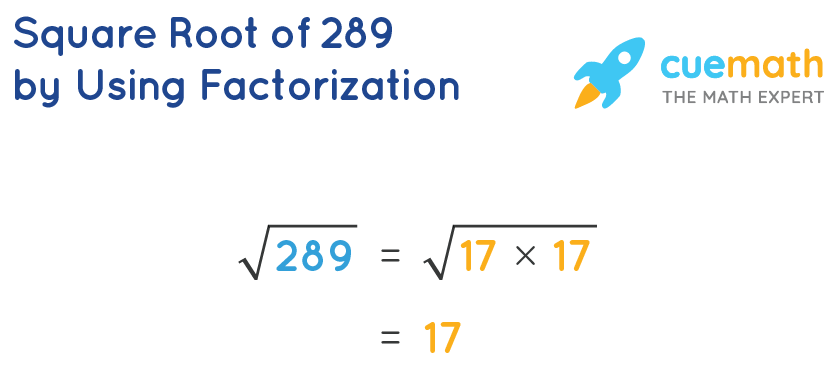
Proof that 17 is the Square Root of 289
To prove that 17 is the square root of 289, we follow these steps:
- Start by stating the definition: The square root of a number \( x \) is a number \( y \) such that \( y \times y = x \).
- Given \( 289 = 17 \times 17 \), we know that \( 17 \) multiplied by itself equals \( 289 \).
- Thus, \( \sqrt{289} = 17 \) by definition because \( 17 \times 17 = 289 \).
This straightforward multiplication verifies that 17 satisfies the condition of being the square root of 289, proving our assertion.
Applications of Square Roots
Square roots find numerous applications in various disciplines:
- Geometry: Calculating the side length of a square given its area, or determining distances in coordinate geometry.
- Physics: Used in equations involving velocity, acceleration, and energy calculations where magnitudes need precise measurement.
- Engineering: Designing structures, calculating forces, and determining dimensions of components in mechanical and civil engineering.
- Finance: In investment calculations such as compound interest and risk assessment where accurate predictions are crucial.
- Computer Science: Algorithms and computations involving matrices, graphics, and simulations rely on square roots for efficiency and accuracy.
- Biology and Medicine: Used in medical imaging, dose calculations, and biological measurements requiring precise quantitative analysis.
The versatility of square roots extends to everyday applications where understanding and manipulating them contribute to problem-solving and innovation across diverse fields.
Perfect Squares Close to 289
Perfect squares near 289 include:
- 256: \( \sqrt{256} = 16 \). It is the closest perfect square less than 289.
- 289: \( \sqrt{289} = 17 \). This is the perfect square we are investigating.
- 324: \( \sqrt{324} = 18 \). It is the closest perfect square greater than 289.
These perfect squares provide benchmarks for comparison and estimation in mathematical calculations and applications where proximity to 289 is significant.
Using Square Roots in Geometry
In geometry, square roots are utilized in various contexts:
- Calculating Side Lengths: Given the area of a square, the side length can be found using the formula \( \text{side length} = \sqrt{\text{area}} \).
- Distance Between Points: In coordinate geometry, the distance between two points \( (x_1, y_1) \) and \( (x_2, y_2) \) is calculated using \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
- Pythagorean Theorem: Essential in right triangles, where \( c \), the hypotenuse, can be found using \( c = \sqrt{a^2 + b^2} \).
- Area and Volume Calculations: Square roots are used to determine the side length of a square given its area, and in calculating the dimensions of three-dimensional shapes like cubes and spheres.
Understanding these applications allows geometric problems to be solved accurately and efficiently, emphasizing the practical use of square roots in geometric calculations.

Using Square Roots in Physics
Square roots play a crucial role in various physics applications, particularly in solving equations involving motion, energy, and waves. Understanding how to calculate and apply square roots can help in comprehending fundamental physical principles. Here are a few key areas where square roots are commonly used:
-
Projectile Motion
In projectile motion, the range (R) of a projectile is given by the formula:
\[ R = \frac{v_0^2 \sin(2\theta)}{g} \]
Here, \(v_0\) is the initial velocity, \(\theta\) is the angle of projection, and \(g\) is the acceleration due to gravity. To find the initial velocity \(v_0\), we often need to take the square root of the product of the range and gravitational constant:
\[ v_0 = \sqrt{\frac{Rg}{\sin(2\theta)}} \]
-
Kinetic Energy
The kinetic energy (KE) of an object is given by:
\[ KE = \frac{1}{2} mv^2 \]
Where \(m\) is the mass and \(v\) is the velocity. To find the velocity from the kinetic energy, the formula is rearranged to:
\[ v = \sqrt{\frac{2KE}{m}} \]
-
Wave Mechanics
In wave mechanics, the speed of a wave (v) is determined by its wavelength (\(\lambda\)) and frequency (f) using the equation:
\[ v = f \lambda \]
If the wave speed is known, the wavelength can be found by rearranging the formula and using the square root:
\[ \lambda = \sqrt{\frac{v}{f}} \]
-
Einstein’s Theory of Relativity
Einstein's theory of relativity involves the use of square roots in the time dilation formula:
\[ t' = \frac{t}{\sqrt{1 - \frac{v^2}{c^2}}} \]
Where \(t'\) is the dilated time, \(t\) is the proper time, \(v\) is the velocity of the moving object, and \(c\) is the speed of light. The square root term accounts for the relativistic effects experienced at high velocities.
By understanding and applying square roots in these contexts, students can better grasp the mathematical foundations underpinning physical phenomena.
Importance of Learning Square Roots
The importance of learning square roots extends across various fields and everyday applications. Understanding square roots is essential for solving mathematical problems and is a foundational concept in algebra and geometry.
- Mathematical Foundation: Square roots are crucial in solving quadratic equations, which are fundamental in advanced math courses. They also play a significant role in understanding the Pythagorean theorem, which relates the lengths of the sides of a right triangle.
- Science and Engineering: In physics, square roots are used to calculate distances, velocities, and forces. For example, the formula for the distance between two points in a plane, derived from the Pythagorean theorem, requires the calculation of a square root. Engineers use square roots to determine the natural frequencies of structures, which helps in designing stable buildings and bridges.
- Statistics: In statistics, square roots are used to calculate standard deviations, which measure the amount of variation or dispersion in a set of values. Understanding standard deviation is critical for data analysis and interpretation.
- Finance: In finance, the concept of volatility, which measures the degree of variation of a trading price series, uses square roots. Volatility is essential for assessing the risk associated with financial instruments.
- Technology and Computer Science: Square roots are used in algorithms for encryption and data security. In computer graphics, square roots are necessary for calculating distances and rendering images accurately.
- Real-Life Problem Solving: Practical applications of square roots include calculating areas and volumes, determining distances, and solving problems in navigation and construction.
By mastering square roots, students and professionals can enhance their problem-solving skills, understand complex concepts in various fields, and apply mathematical principles to real-world situations.
Conclusion
The exploration of the square root of 289 has highlighted the importance and utility of understanding square roots in mathematics. We have established that the square root of 289 is 17, a perfect square, which simplifies various calculations and demonstrates the elegance of mathematical relationships.
Learning square roots, such as 17 for 289, is crucial for several reasons:
- Simplification of Calculations: Understanding square roots helps in simplifying complex mathematical problems, making it easier to work with large numbers and perform arithmetic operations.
- Algebraic Applications: Square roots are fundamental in solving quadratic equations, a critical aspect of algebra that has applications in numerous fields such as physics, engineering, and economics.
- Geometric Insights: Knowledge of square roots aids in understanding geometric concepts, particularly those involving areas and volumes. For instance, calculating the side length of a square with a given area becomes straightforward with the knowledge of square roots.
- Physical Sciences: Square roots are used in various physics formulas, such as those involving the calculation of energy, wave frequencies, and statistical analysis of data.
- Analytical Skills: Learning and applying square roots enhance analytical thinking and problem-solving skills, which are valuable in both academic and real-world scenarios.
Overall, the study of square roots, exemplified by the square root of 289, fosters a deeper appreciation for mathematics and its applications. It underscores the interconnectedness of different mathematical concepts and their practical relevance, encouraging continuous learning and exploration.
Video giải thích cách tính căn bậc hai của 289 bằng tiếng Việt.
Căn Bậc Hai của 289
READ MORE:
Video hướng dẫn cách tính căn bậc hai của 289 bằng phương pháp phân tích thừa số nguyên tố bằng tiếng Việt.
Căn Bậc Hai Của 289 Bằng Phương Pháp Phân Tích Thừa Số Nguyên Tố