What is 256 Squared? Discover the Fascinating Answer!

Calculating the square of 256 involves multiplying the number by itself. Here is the detailed calculation:

Mathematical Expression

To find the square of 256, we use the following expression:

\[
256^2 = 256 \times 256
\]

Step-by-Step Calculation

1. First, decompose 256 into smaller components for easier multiplication:
   • 256 = 200 + 50 + 6
2. Next, apply the distributive property to calculate the product:
   • \[ (200 + 50 + 6)^2 = 200^2 + 2 \cdot 200 \cdot 50 + 2 \cdot 200 \cdot 6 + 50^2 + 2 \cdot 50 \cdot 6 + 6^2 \]
   • Calculate each term separately:
   • \[ 200^2 = 40000 \]
   • \[ 2 \cdot 200 \cdot 50 = 20000 \]
   • \[ 2 \cdot 200 \cdot 6 = 2400 \]
   • \[ 50^2 = 2500 \]
   • \[ 2 \cdot 50 \cdot 6 = 600 \]
   • \[ 6^2 = 36 \]
3. Finally, add all the terms together to get the final result:
   • \[ 40000 + 20000 + 2400 + 2500 + 600 + 36 = 65536 \]

Result

Therefore, the square of 256 is:

\[
256^2 = 65536
\]

Squaring a number involves multiplying the number by itself. This fundamental operation in mathematics results in a new value that is the area of a square with sides of the given length. For instance, 256 squared, denoted as \(256^2\) or \(256 \times 256\), equals 65,536. Squaring numbers is crucial in various fields such as algebra, geometry, and computing.

The square of a number can be represented in different forms:

• Multiplication form: \(256 \times 256\)
• Exponential form: \(256^2\)

Squaring a number has several important properties:

• It always produces a positive result.
• The square of an even number is always even.
• The square of an odd number is always odd.

Here are some identities related to squaring numbers:

• Square of a sum: \((a + b)^2 = a^2 + 2ab + b^2\)
• Square of a difference: \((a - b)^2 = a^2 - 2ab + b^2\)

Squaring numbers also plays a significant role in computing and digital technology, especially when dealing with binary systems and memory architecture. For example, 256 is a power of 2, specifically \(2^8\), making it an important number in binary systems where it represents the number of distinct values in an 8-bit byte.

Squaring a number is a fundamental arithmetic operation that involves multiplying the number by itself. This operation is denoted as \( n^2 \), where \( n \) is the number being squared. The result is known as the "square" of the number.

• For example, squaring the number 256 is expressed as \( 256^2 \).
• Mathematically, this is calculated as \( 256 \times 256 \).

The concept of squaring numbers is essential in various fields of mathematics and practical applications:

1. Geometry: The area of a square with side length \( n \) is given by \( n^2 \). For instance, a square with each side measuring 256 units has an area of \( 256^2 = 65,536 \) square units.
2. Algebra: Squaring is used to solve quadratic equations and in polynomial expressions.
3. Number Theory: Squaring numbers helps in understanding properties of integers, such as perfect squares. A number is a perfect square if it can be expressed as \( n^2 \), where \( n \) is an integer. For instance, 256 is a perfect square because \( 256 = 16^2 \).
4. Computing: In digital systems, squaring is used in algorithms and cryptographic functions. For example, the number 256 is significant in computing because it represents \( 2^8 \), which is the number of distinct values that can be represented with an 8-bit byte.

Understanding how to square numbers and the implications of this operation is crucial for mathematical literacy and practical problem-solving in various disciplines.

Squaring a number means multiplying the number by itself. It is a fundamental operation in mathematics that results in a new value, which represents the area of a square with sides of the given length.

Mathematically, the operation is defined as:

\[ n^2 = n \times n \]

For any integer \( n \), its square \( n^2 \) is obtained by multiplying \( n \) by itself.

For example, when squaring 256:

\[ 256^2 = 256 \times 256 = 65536 \]

This operation can be broken down into several steps:

• Multiply the units digit of the number by itself.
• Multiply the tens digit of the number by itself, including any carry-over from the units multiplication.
• Repeat for hundreds, thousands, etc., summing all the results appropriately.

In general terms, the process can be illustrated with smaller numbers for simplicity:

For \( n = 12 \):

1. \( 12^2 = 12 \times 12 \)
2. Multiply the units: \( 2 \times 2 = 4 \)
3. Multiply the tens: \( 10 \times 12 = 120 \)
4. Sum the results: \( 4 + 120 = 144 \)

This same principle applies to larger numbers such as 256, but the multiplication becomes more complex, often necessitating the use of a calculator for efficiency.

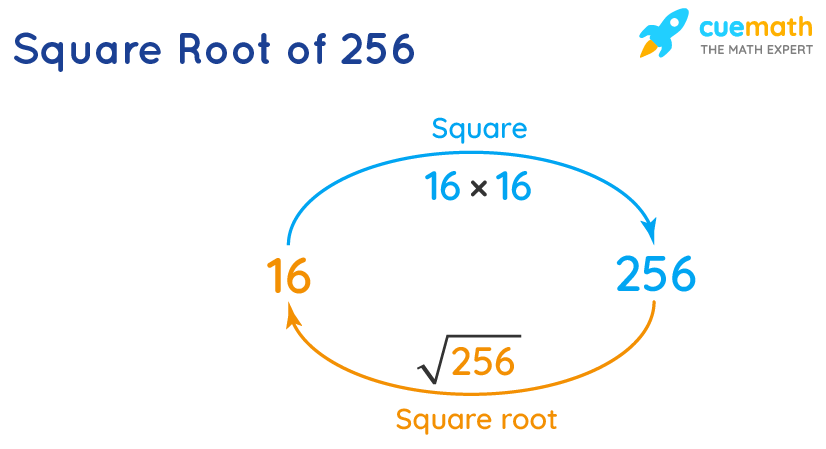
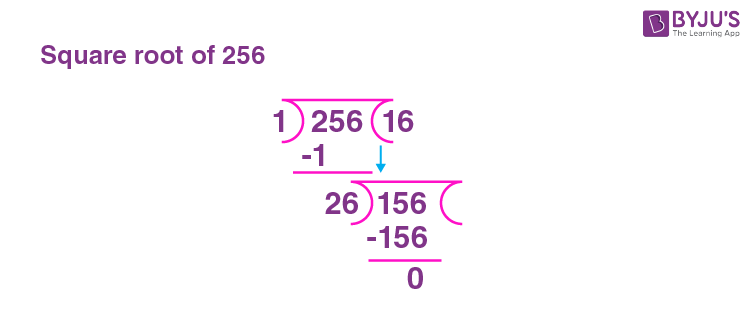
Another important concept related to squaring is the relationship between squares and square roots. The square root of a number \( x \) is a value \( y \) such that:

\[ y^2 = x \]

For example, since \( 16^2 = 256 \), the square root of 256 is 16.

Squaring numbers is not only a key operation in basic arithmetic but also has significant applications in various fields including geometry, computer science, and engineering, where it is used to calculate areas, perform encryption, and analyze data.

To calculate the square of 256, we follow these detailed steps:

1. First, understand that squaring a number means multiplying the number by itself. For 256, this means calculating \( 256 \times 256 \).
2. We can break down the multiplication for clarity:

Using the distributive property of multiplication:

\[ (256)^2 = 256 \times 256 \]

We split 256 into (250 + 6) for easier multiplication:

\[ (250 + 6) \times (250 + 6) \]

Apply the distributive property (FOIL method):

1. \[ 250 \times 250 = 62500 \]
2. \[ 250 \times 6 = 1500 \]
3. \[ 6 \times 250 = 1500 \]
4. \[ 6 \times 6 = 36 \]

Add all the products together:

\[ 62500 + 1500 + 1500 + 36 = 65536 \]

So, the square of 256 is:

\[ 256^2 = 65536 \]

We can verify this result by using another method. Let's consider the formula for squaring:

\[ (n + m)^2 = n^2 + 2nm + m^2 \]

Where \( n = 250 \) and \( m = 6 \), then:

1. \[ n^2 = 250^2 = 62500 \]
2. \[ 2nm = 2 \times 250 \times 6 = 3000 \]
3. \[ m^2 = 6^2 = 36 \]

Adding these values together confirms our calculation:

\[ 62500 + 3000 + 36 = 65536 \]

Therefore, the final result is:

\[ (256)^2 = 65536 \]

The step-by-step calculation confirms that the square of 256 is 65536. This detailed breakdown ensures clarity and understanding of the process.

Calculating the square of 256 involves multiplying the number by itself. Here, we will break down this process step by step.

1. First, understand that squaring a number means multiplying the number by itself. In mathematical terms, squaring 256 is represented as \(256^2\).
2. Set up the multiplication:
   • \(256 \times 256\)
3. To simplify, break down 256 into smaller parts using the distributive property:
   • \(256 = 200 + 50 + 6\)
4. Apply the distributive property:
   • \((200 + 50 + 6) \times (200 + 50 + 6)\)
5. Expand the expression using the distributive property:
   • \((200 \times 200) + (200 \times 50) + (200 \times 6) + (50 \times 200) + (50 \times 50) + (50 \times 6) + (6 \times 200) + (6 \times 50) + (6 \times 6)\)
6. Calculate each term:
   • \(200 \times 200 = 40000\)
   • \(200 \times 50 = 10000\)
   • \(200 \times 6 = 1200\)
   • \(50 \times 200 = 10000\)
   • \(50 \times 50 = 2500\)
   • \(50 \times 6 = 300\)
   • \(6 \times 200 = 1200\)
   • \(6 \times 50 = 300\)
   • \(6 \times 6 = 36\)
7. Add all the terms together:
   • \(40000 + 10000 + 1200 + 10000 + 2500 + 300 + 1200 + 300 + 36 = 65536\)

Thus, \(256^2 = 65536\).

To understand the process of squaring 256, we break it down into intermediate steps that simplify the calculation. Here is a detailed step-by-step breakdown:

1. Start with the basic multiplication of 256 by itself:

   \( 256 \times 256 \)

2. Decompose 256 into a sum of simpler numbers:

   \( 256 = 250 + 6 \)

3. Apply the distributive property of multiplication:

   \( (250 + 6) \times (250 + 6) = 250^2 + 2 \times 250 \times 6 + 6^2 \)

4. Calculate each term separately:
   • \( 250^2 = 62500 \)
   • \( 2 \times 250 \times 6 = 3000 \)
   • \( 6^2 = 36 \)
5. Add the results of the intermediate calculations:

   \( 62500 + 3000 + 36 = 65536 \)

Thus, the square of 256 is:

\[ 256^2 = 65536 \]

This method ensures accuracy and demonstrates the application of basic arithmetic properties in breaking down complex calculations.

To find the square of 256, we follow these steps:

1. Start with the given number: \( 256 \).

2. Multiply the number by itself: \( 256 \times 256 \).

3. Perform the multiplication step-by-step:

   • First, multiply the digits in the units place: \( 6 \times 6 = 36 \). Write down 6 and carry over 3.

   • Next, multiply the digit in the tens place with the units place and add the carry: \( 5 \times 6 + 3 = 33 \). Write down 3 and carry over 3.

   • Continue with the hundreds place: \( 2 \times 6 + 3 = 15 \). Write down 5 and carry over 1. The partial result is 1536.

   • Repeat the process for the next row, shifting one place to the left for each digit in the tens place of the multiplier.

4. Sum the partial results:

   256	×	256
   		1536
   	+ 5120
   + 102400
   =	65536

5. The final result of \( 256^2 \) is \( 65536 \).

Squaring numbers is a fundamental mathematical operation that has numerous real-world applications across various fields. Here are some key examples:

• Science
  • Genetics: Squaring helps calculate the number of possible genotypes for a genetic trait. For instance, the number of combinations in a genetic cross can be determined using squared values.
  • Chemistry: Squaring is used in calculating the molar mass of compounds, aiding in stoichiometric calculations and understanding molecular structures.
• Engineering
  • Electrical Engineering: Power calculations in electrical circuits often require squaring the voltage or current values to determine power output.
  • Structural Engineering: Squaring is used to calculate load-bearing capacities and stresses in materials, essential for safe structural designs.
• Finance
  • Investment Analysis: Compounded returns over multiple periods are calculated using squared values, helping investors understand long-term profitability.
  • Risk Assessment: Squaring is used in calculating variance and standard deviation, which are crucial for assessing the risk and volatility of investments.
• Statistics
  • In statistical analysis, squares are used to calculate variance and standard deviation, helping to understand the dispersion and central tendency of data sets.
• Geometry
  • Squares and square roots are employed to compute areas and perimeters of shapes, and to solve problems involving right triangles, such as in the Pythagorean theorem.
• Computer Science
  • In computer programming, squares are used in algorithms for encryption, image processing, and game physics, among other applications.
• Cryptography
  • Squares and square roots are used in digital signatures, key exchange systems, and secure communication protocols, ensuring data security.
• Navigation
  • Pilots and navigators use squares to compute distances and bearings between points on maps, crucial for accurate navigation and planning.
• Telecommunication
  • The inverse square law is used to model how signal strength decreases with distance from a transmitter, essential for designing effective communication systems.

Squaring numbers, such as calculating \( 256^2 \), is fundamental in mathematics for several reasons:

1. Foundation of Exponential Growth: Squaring serves as a building block for understanding exponential growth and power functions.
2. Area and Volume Calculations: In geometry, squaring is crucial for calculating areas of squares and volumes of cubes.
3. Statistical Analysis: Squaring plays a role in statistical analysis, particularly in variance calculations.
4. Physical Laws: In physics, squaring is used to express laws such as the inverse square law of gravitation and optics.
5. Computer Science: Squaring is utilized in algorithms and computations, often in optimization problems and cryptographic functions.

Understanding squaring not only enhances basic arithmetic skills but also provides a foundation for advanced mathematical concepts and practical applications across various disciplines.

Squaring numbers, such as calculating \( 256^2 \), finds practical applications in everyday situations:

• Area Measurement: Calculating the area of a square room or a plot of land.
• Financial Planning: Determining compound interest and growth rates.
• Engineering: Calculating power requirements and structural load capacities.
• Technology: In digital imaging and resolution calculations.
• Science: Modeling natural phenomena like sound intensity or light intensity.

Understanding squaring enables individuals to make informed decisions and solve practical problems efficiently in various aspects of daily life.

Exploring advanced mathematical concepts related to squaring, especially with \( 256^2 \) as an example, involves:

1. Power Functions: Understanding squaring as a basic form of power functions, essential for higher-order polynomials.
2. Matrix Operations: In linear algebra, squaring matrices is fundamental for eigenvalue calculations and matrix transformations.
3. Number Theory: Squaring plays a role in modular arithmetic and cryptographic algorithms.
4. Complex Analysis: In complex numbers, squaring relates to the modulus and argument transformations.
5. Differential Equations: Squaring appears in solutions involving second-order derivatives and differential operators.

Mastering these concepts not only deepens understanding of squaring but also forms the basis for more advanced mathematical explorations and applications in diverse fields.

Comparing squaring with other exponential operations, such as \( 256^2 \), highlights:

• Cubic and Higher Powers: Squaring is a specific case of exponentiation where the exponent is 2, contrasting with higher powers like cubing (exponent 3) and beyond.
• Exponential Growth: Unlike linear growth, squaring represents exponential growth, where the result increases rapidly with each iteration.
• Root Operations: Inversely related to squaring are square root operations, which aim to find the original number when squared.
• Logarithmic Functions: Squaring connects with logarithmic functions, specifically the quadratic relationship in logarithmic scales.
• Applications in Physics: In physics, squaring appears in the context of energy equations and wave functions, showing its broad utility.

Understanding these comparisons illuminates the distinct role of squaring in mathematics and its applications across various disciplines.

Visualizing squared numbers, such as \( 256^2 \), can be understood through:

• Geometric Representation: Squaring a number corresponds to forming a square with sides equal to the number's value, showcasing an area calculation.
• Graphical Interpretation: Plotting the function \( f(x) = x^2 \) reveals a parabola that opens upwards, demonstrating the rapid increase in values as x grows.
• Real-World Examples: Imagine squaring the side length of a square to find its total area or squaring time to compute the area under a velocity-time graph.
• Mathematical Models: Using visual aids like tables or graphs helps in understanding the relationship between a number and its squared value.
• Conceptual Understanding: Visualizing squared numbers enhances comprehension of exponential growth and its applications in various fields.

These visualizations not only aid in mathematical education but also provide insight into the practical implications of squaring in everyday scenarios.

Graphically representing \( 256^2 \) provides a visual insight into its exponential growth:

• Plotting the Function: The graph of \( f(x) = x^2 \) for \( x = 256 \) forms a parabola that opens upwards.
• Vertex of the Parabola: The vertex of the parabola occurs at \( (256, 65536) \), indicating the maximum squared value at this point.
• Rate of Increase: The steepness of the curve illustrates how squaring amplifies numbers quickly, reflecting exponential growth.
• Comparative Analysis: Contrasting with linear and other exponential functions, the graphical representation emphasizes the rapid growth unique to squaring.
• Practical Applications: Understanding this graphical representation aids in fields like physics, economics, and engineering where exponential growth models are essential.

Visualizing \( 256^2 \) graphically enriches comprehension of its mathematical properties and practical implications across various disciplines.

Interactive tools for understanding squaring, such as \( 256^2 \), offer engaging ways to grasp its concepts:

• Virtual Manipulatives: Online tools allow users to input numbers and instantly see their squares, aiding in visual and tactile learning.
• Graphical Simulations: Dynamic graphs illustrate how squaring transforms linear increases into exponential growth, enhancing conceptual understanding.
• Interactive Games: Educational games incorporate squaring challenges, making learning enjoyable and reinforcing mathematical skills.
• Step-by-Step Calculators: Tools provide detailed calculations and explanations, guiding users through the process of squaring numbers.
• Mobile Applications: Apps offer portable access to tools that demonstrate squaring and its applications in daily life and advanced mathematics.

Utilizing these interactive tools fosters a deeper appreciation for squaring's significance and facilitates mastery of related mathematical concepts across diverse learning environments.

In conclusion, exploring \( 256^2 \) and squaring numbers reveals:

• Mathematical Foundation: Squaring is fundamental, forming the basis for exponential growth and power functions.
• Practical Applications: It finds extensive use in geometry, physics, engineering, and everyday calculations.
• Visual and Graphical Representations: Visualizing squaring enhances understanding through geometric shapes and graphical plots.
• Advanced Concepts: It connects with complex mathematical concepts like matrices, differential equations, and number theory.
• Interactive Learning Tools: Online resources and applications provide interactive ways to explore and apply squaring.

By mastering the concept of squaring, individuals gain a versatile tool for solving problems, analyzing data, and understanding the world through a mathematical lens.