Topic square root of 36: The square root of 36 is a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the product 36. This article will explore its properties, calculation methods, and real-world applications, making it easy for anyone to understand and appreciate the importance of this mathematical constant.
Table of Content
- Square Root of 36
- Introduction to Square Roots
- What is the Square Root of 36?
- Properties of the Square Root of 36
- Mathematical Calculation of the Square Root of 36
- Visualizing the Square Root of 36
- Applications of the Square Root of 36
- Common Misconceptions about Square Roots
- Practice Problems Involving the Square Root of 36
- Conclusion
- YOUTUBE: Video này giải thích chi tiết về căn bậc hai của 36, giúp người xem hiểu rõ hơn về khái niệm này.
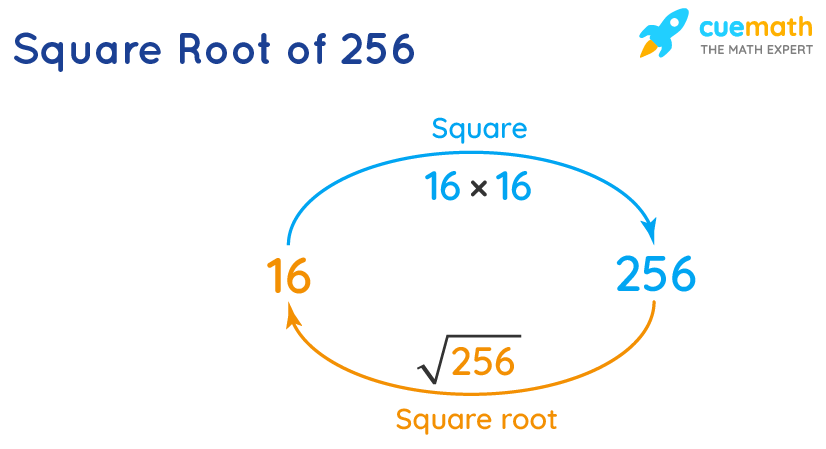
Square Root of 36
The square root of 36 is represented by the symbol \( \sqrt{36} \). When you calculate it, you find that:
\[ \sqrt{36} = 6 \]
So, the square root of 36 is 6.
READ MORE:
Introduction to Square Roots
The concept of a square root is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. The square root is denoted by the radical symbol √. For example, the square root of 36 is represented as √36.
Here are some key points to understand about square roots:
- A square root of a number n is a number x such that \( x^2 = n \).
- Every positive number has two square roots: one positive and one negative. For example, the square roots of 36 are 6 and -6.
- The principal square root is the non-negative square root, which is typically what is referred to when discussing square roots.
Steps to find the square root of a number:
- Identify the number you want to find the square root of (e.g., 36).
- Determine the factors of the number to see if it's a perfect square (36 = 6 × 6).
- Use the radical symbol to express the square root (√36 = 6).
Let's look at a comparison table of some common square roots:
| Number | Square Root |
|---|---|
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
Understanding square roots is essential for solving quadratic equations, simplifying expressions, and various applications in science and engineering.
What is the Square Root of 36?
The square root of 36 is a fundamental mathematical concept that can be understood through its definition and properties. The square root of a number is a value that, when multiplied by itself, yields the original number. For 36, the square root is 6 because \(6 \times 6 = 36\).
Here is a step-by-step explanation of finding the square root of 36:
- Identify the number you want to find the square root of. In this case, it is 36.
- Recognize that you need to find a number that, when squared, equals 36.
- Recall the multiplication table or use a factorization method to determine that \(6 \times 6 = 36\).
- Therefore, the square root of 36 is 6, which can be written mathematically as \(\sqrt{36} = 6\).
It is also important to note that every positive number has two square roots: a positive and a negative one. Thus, for 36, the square roots are 6 and -6, since \((6) \times (6) = 36\) and \((-6) \times (-6) = 36\).
Let's illustrate this with a simple table:
| Number | Positive Square Root | Negative Square Root |
|---|---|---|
| 36 | 6 | -6 |
In summary, the principal square root of 36 is 6, but the number also has a negative square root of -6. Understanding this helps in solving various mathematical problems and equations.
Properties of the Square Root of 36
The square root of 36 has several interesting properties that are fundamental to understanding its mathematical significance. Here, we explore these properties in detail:
- Principal Square Root: The principal (or positive) square root of 36 is 6, which is represented as \(\sqrt{36} = 6\).
- Negative Square Root: The negative square root of 36 is -6, since \((-6) \times (-6) = 36\). This can be represented as \(-\sqrt{36} = -6\).
- Perfect Square: Since 36 is a perfect square (6 × 6 = 36), its square root is an integer. Perfect squares have whole numbers as their square roots.
- Rational Number: The square root of 36 is a rational number because it can be expressed as a fraction (6/1 or -6/1).
- Non-Negative Principal Root: By convention, the principal square root is always non-negative. Thus, when referring to \(\sqrt{36}\), we typically mean the positive root 6.
To better understand these properties, let's summarize them in a table:
| Property | Description |
|---|---|
| Principal Square Root | 6 |
| Negative Square Root | -6 |
| Perfect Square | Yes, because 36 = 6 × 6 |
| Rational Number | Yes, 6/1 or -6/1 |
| Non-Negative Principal Root | 6 |
These properties make the square root of 36 a fundamental example in mathematics, illustrating the behavior of square roots for perfect squares and the nature of rational numbers.
Mathematical Calculation of the Square Root of 36
Calculating the square root of 36 is a straightforward process that can be understood through various mathematical methods. Here, we outline a step-by-step approach to find the square root of 36:
- Identify the Number: The first step is to identify the number for which we need to find the square root. In this case, the number is 36.
- Prime Factorization Method: One way to find the square root is through prime factorization. We break down 36 into its prime factors:
- 36 = 2 × 2 × 3 × 3
- (2 × 2) and (3 × 3)
- 2 and 3
- 2 × 3 = 6
- Using the Exponent Method: Another way to find the square root is by using the exponent method. Any number raised to the power of 1/2 gives its square root. Therefore,
\(36^{1/2} = 6\).
- Verification: To verify, we can square the result to check if it equals the original number:
\(6 \times 6 = 36\).
This confirms that the square root of 36 is indeed 6.
To summarize, the square root of 36 can be calculated through different methods such as prime factorization and the exponent method. Both methods lead to the same result:
| Method | Calculation | Result |
|---|---|---|
| Prime Factorization | 36 = 2 × 2 × 3 × 3 → 2 × 3 = 6 | 6 |
| Exponent Method | 36^{1/2} | 6 |
| Verification | 6 × 6 | 36 |
Thus, through these methods, we can clearly see that the square root of 36 is 6.
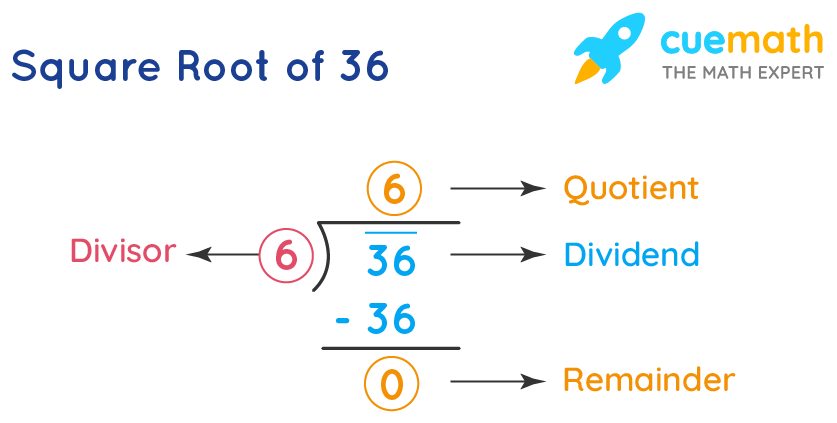
Visualizing the Square Root of 36
Visualizing the square root of 36 can help in understanding its significance and applications. Here are some ways to visualize and interpret the square root of 36:
- Number Line Representation:
One of the simplest ways to visualize the square root of 36 is on a number line. Place 0 at the center and mark 36 on the line. The square root of 36 is 6, so you would place a point at 6 on the number line. Since -6 is also a square root, mark -6 as well. This shows that both 6 and -6 are equidistant from 0 and when squared, they return 36.
- 0 — 6 — 36
- 0 — (-6) — 36
- Geometric Representation:
Another way to visualize the square root of 36 is geometrically. Consider a square with an area of 36 square units. The length of each side of this square is the square root of 36. Therefore, each side is 6 units long. This can be illustrated as:
6 units - Graphical Representation:
A graph of the function \(y = \sqrt{x}\) can also help visualize the square root of 36. Plot the point where \(x = 36\). The corresponding \(y\)-value will be 6. This point on the graph confirms that \(\sqrt{36} = 6\).
- Point: (36, 6)
- Area Model:
Visualize a 6x6 grid to represent the area. Each small square in the grid is 1 unit by 1 unit, and the entire grid contains 36 squares. The side length of the grid, 6, is the square root of 36.
These visual methods help reinforce the concept that the square root of 36 is 6, providing a more intuitive understanding of this mathematical principle.
Applications of the Square Root of 36
The square root of 36 has various practical applications across different fields. Understanding these applications helps in appreciating the importance of this mathematical concept. Here are some key areas where the square root of 36 is applied:
- Geometry:
In geometry, the square root of 36 is used to calculate the side length of squares. For instance, if a square has an area of 36 square units, each side length is 6 units, since \(\sqrt{36} = 6\).
- Trigonometry:
In trigonometry, the square root of 36 can be involved in solving problems related to right-angled triangles. If the square of the hypotenuse or any leg is 36, then the length of that side is 6 units.
- Physics:
In physics, the square root of 36 may be used in formulas involving areas and distances. For example, if the kinetic energy equation \(KE = \frac{1}{2}mv^2\) involves a velocity squared value of 36, the velocity is 6 units (assuming appropriate units).
- Engineering:
Engineers use the square root of 36 in various calculations, such as determining the dimensions of components. For example, if a component's cross-sectional area is 36 square units, its dimension can be 6 units by 6 units.
- Algebra:
In algebra, solving equations often involves taking square roots. If an equation results in \(x^2 = 36\), then \(x = \pm 6\), showing the solutions involve the square root of 36.
- Everyday Calculations:
In everyday life, the square root of 36 can help in making estimations and calculations. For instance, if you need to determine the side length of a square garden with an area of 36 square feet, it is 6 feet.
These applications highlight the utility of the square root of 36 in various disciplines, demonstrating its broad relevance and importance in both academic and practical contexts.
Common Misconceptions about Square Roots
Understanding square roots is crucial in mathematics, but there are several common misconceptions that can lead to confusion. Here we address and clarify these misconceptions to provide a clear understanding:
- Square Roots are Always Positive:
One common misconception is that square roots are always positive. While the principal square root is positive, every positive number actually has two square roots: one positive and one negative. For example, the square roots of 36 are 6 and -6, since both \(6^2 = 36\) and \((-6)^2 = 36\).
- Square Root of Negative Numbers:
Another misconception is that negative numbers cannot have square roots. While it is true that real numbers do not have real square roots for negative values, in the context of complex numbers, they do. For instance, the square root of -36 is 6i, where i is the imaginary unit (\(i^2 = -1\)).
- Square Root and Squaring are Inverse Operations:
It is often misunderstood that taking the square root and squaring a number are perfect inverse operations without exceptions. However, while \(\sqrt{x^2} = |x|\), this includes both positive and negative roots, reflecting that squaring removes the sign information.
- Rational and Irrational Roots:
There is a misconception that all square roots are irrational. While many square roots are irrational (e.g., \(\sqrt{2}\)), perfect squares (such as 36) have rational square roots. Thus, \(\sqrt{36} = 6\), a rational number.
- Misinterpretation of Symbols:
Misunderstanding the symbol \(\sqrt{}\) is common. This symbol refers to the principal square root, which is the non-negative root. For example, \(\sqrt{36} = 6\), not -6. However, acknowledging that the equation \(x^2 = 36\) has two solutions (x = 6 and x = -6) is essential.
Clarifying these misconceptions helps in a better understanding of square roots and their properties, ensuring accurate mathematical reasoning and problem-solving.
Practice Problems Involving the Square Root of 36
To solidify your understanding of the square root of 36, here are several practice problems. These problems will help you apply the concept in different scenarios.
- Problem 1: Simplify the expression \( \sqrt{36} \).
- Solution: The square root of 36 is 6 since \( 6 \times 6 = 36 \).
- Problem 2: If \( x = \sqrt{36} \), what is \( x^2 \)?
- Solution: Since \( x = 6 \), \( x^2 = 6^2 = 36 \).
- Problem 3: Find the value of \( \sqrt{36} + \sqrt{36} \).
- Solution: \( \sqrt{36} = 6 \). Therefore, \( 6 + 6 = 12 \).
- Problem 4: Solve for \( y \) in the equation \( y^2 = 36 \).
- Solution: \( y = \pm 6 \) since both \( 6^2 = 36 \) and \( (-6)^2 = 36 \).
- Problem 5: Evaluate \( \frac{\sqrt{36}}{2} \).
- Solution: \( \sqrt{36} = 6 \). Therefore, \( \frac{6}{2} = 3 \).
Advanced Problems
- Problem 6: If \( z = \sqrt{36} \) and \( w = \sqrt{16} \), find \( z + w \).
- Solution: \( \sqrt{36} = 6 \) and \( \sqrt{16} = 4 \). Therefore, \( z + w = 6 + 4 = 10 \).
- Problem 7: Solve the equation \( 2x^2 - 12 = 0 \).
- Solution: First, add 12 to both sides to get \( 2x^2 = 12 \). Then, divide both sides by 2 to get \( x^2 = 6 \). Finally, take the square root of both sides to find \( x = \pm \sqrt{6} \).
- Problem 8: The area of a square is 36 square units. What is the length of one side of the square?
- Solution: The side length of a square is given by the square root of its area. Therefore, \( \text{side length} = \sqrt{36} = 6 \) units.
These practice problems cover basic and advanced applications of the square root of 36, helping you reinforce your understanding and problem-solving skills.
Conclusion
The square root of 36 is an essential concept in mathematics, illustrating fundamental properties of numbers. Recognizing that the square root of 36 is 6 helps in understanding perfect squares, the relationship between squares and square roots, and the practical applications in various fields such as geometry, algebra, and real-world problem-solving.
Key takeaways include:
- The square root of 36, expressed as √36, equals 6.
- 36 is a perfect square, which means it is the product of an integer multiplied by itself (6 × 6 = 36).
- The properties of square roots help simplify and solve equations, making them crucial in both academic and everyday contexts.
By mastering the concept of square roots, particularly through examples like √36, students and professionals alike can enhance their mathematical proficiency and problem-solving skills. This foundational knowledge serves as a stepping stone for more advanced mathematical learning and applications.
Video này giải thích chi tiết về căn bậc hai của 36, giúp người xem hiểu rõ hơn về khái niệm này.
Căn Bậc Hai Của 36
READ MORE:
Video này giải thích tại sao căn bậc hai của 36 chỉ là 6 dương, mang lại cái nhìn sâu sắc về lý do toán học đằng sau.
Tại Sao Căn Bậc Hai của 36 Chỉ Là 6 Dương