Topic what is the square of 36: The square of 36 is a fundamental mathematical concept with various applications in real life. By understanding how to calculate it and its properties, you can enhance your problem-solving skills. In this article, we'll explore the steps to find the square of 36, its significance, and where it is commonly used.
Table of Content
- What is the Square of 36?
- Introduction to Squaring Numbers
- Definition and Concept of Squaring
- Mathematical Calculation of the Square of 36
- Properties of Squaring Numbers
- Applications of Squaring in Real Life
- Visual Representation of Squaring
- Comparison with Other Squares
- Common Mistakes in Squaring Numbers
- Practice Problems and Examples
- Conclusion
- YOUTUBE: Video giải thích tại sao căn bậc hai của 36 chỉ là 6 dương. Khám phá toán học và những khái niệm quan trọng liên quan đến căn bậc hai.
What is the Square of 36?
The square of a number is obtained by multiplying the number by itself. For the number 36, the square is calculated as follows:
\[
36^2 = 36 \times 36 = 1296
\]
Steps to Calculate the Square of 36
- Start with the number 36.
- Multiply 36 by itself: \[ 36 \times 36 \]
- The result is 1296.
Properties of Squaring
- Squaring a positive number results in a positive number.
- Squaring a negative number also results in a positive number.
- The square of zero is zero.
| Number | Square |
| 36 | 1296 |
Therefore, the square of 36 is 1296.
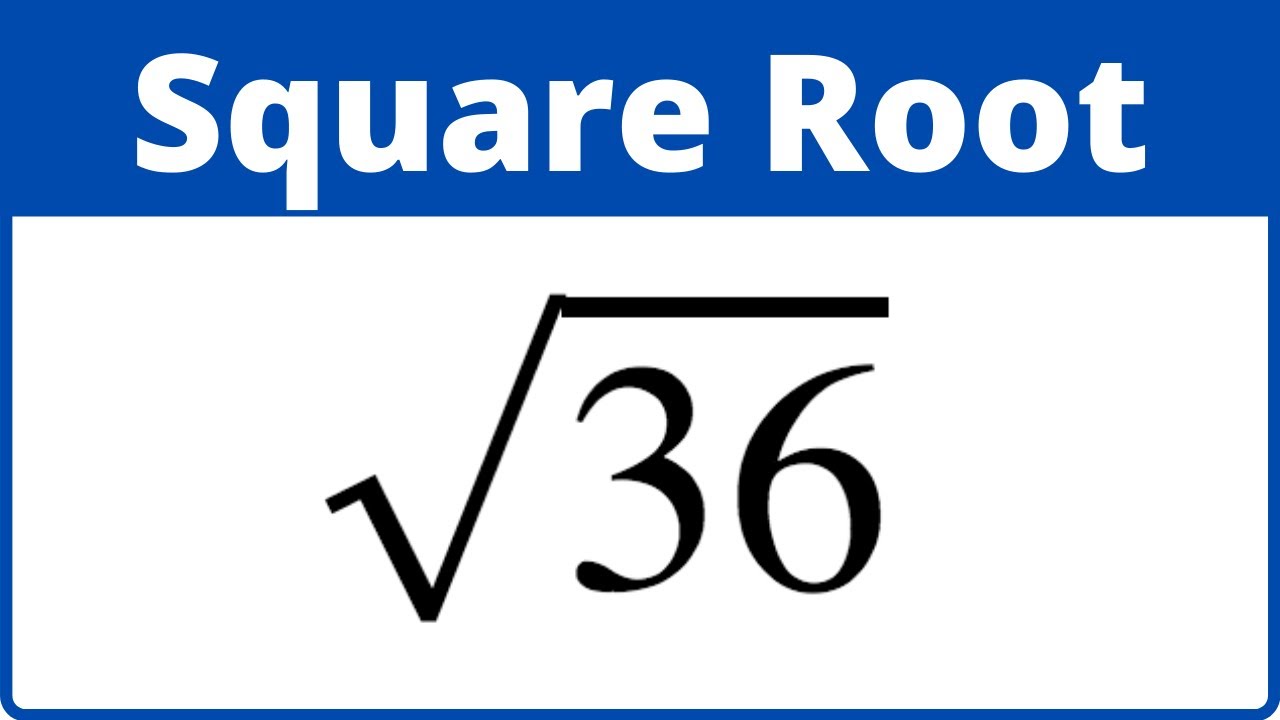
READ MORE:
Introduction to Squaring Numbers
Squaring a number is a fundamental mathematical operation that involves multiplying the number by itself. This operation is represented by a superscript "2" placed next to the number. For example, the square of 36 is written as 362. Understanding how to square numbers is essential for various mathematical concepts and real-life applications.
Here are the steps to square a number:
- Identify the number you want to square. In this case, the number is 36.
- Multiply the number by itself: \[ 36 \times 36 \]
- The result is the square of the number. For 36, this calculation gives: \[ 36^2 = 1296 \]
Squaring numbers is not only a basic arithmetic operation but also has several important properties and applications:
- Squaring a positive number results in a positive number.
- Squaring a negative number also results in a positive number because \[ (-a)^2 = a^2 \]
- The square of zero is zero: \[ 0^2 = 0 \]
Squaring numbers is used in various fields such as geometry (calculating the area of squares), physics (determining force and energy), and statistics (variance and standard deviation calculations).
Definition and Concept of Squaring
Squaring a number means multiplying that number by itself. This operation is denoted using the exponent 2. For example, the square of a number \(a\) is written as \(a^2\) and calculated as \(a \times a\).
To understand squaring, let's break it down step by step:
- Start with a number. For this example, we'll use 36.
- Multiply the number by itself: \[ 36 \times 36 \]
- The result of this multiplication is the square of the number: \[ 36^2 = 1296 \]
The concept of squaring extends to several important mathematical properties:
- Positive Numbers: The square of a positive number is always positive. For instance, \[ 5^2 = 25 \]
- Negative Numbers: The square of a negative number is also positive because multiplying two negative numbers results in a positive number. For example, \[ (-5)^2 = 25 \]
- Zero: The square of zero is zero: \[ 0^2 = 0 \]
Squaring numbers is a fundamental operation in mathematics with applications in various fields such as:
- Geometry: Calculating the area of squares.
- Algebra: Working with quadratic equations.
- Physics: Determining kinetic energy and other properties.
- Statistics: Calculating variance and standard deviation.
Mathematical Calculation of the Square of 36
Calculating the square of a number involves multiplying the number by itself. For the number 36, this can be done using straightforward multiplication. Let's break down the steps in detail:
- Identify the number you want to square, which in this case is 36.
- Multiply the number by itself: \[ 36 \times 36 \]
- Perform the multiplication step-by-step:
- First, multiply 6 (units place) by 36: \[ 6 \times 36 = 216 \]
- Next, multiply 30 (tens place) by 36: \[ 30 \times 36 = 1080 \]
- Add the two products together: \[ 216 + 1080 = 1296 \]
Thus, the square of 36 is:
\[
36^2 = 1296
\]
We can also represent this calculation in a tabular format for clarity:
| Step | Calculation | Result |
| 1 | 6 × 36 | 216 |
| 2 | 30 × 36 | 1080 |
| 3 | 216 + 1080 | 1296 |
Therefore, the mathematical calculation of the square of 36 confirms that:
\[
36^2 = 1296
\]
Properties of Squaring Numbers
Squaring numbers is a basic mathematical operation with several interesting properties. Understanding these properties can help in various mathematical computations and problem-solving scenarios.
- Always Non-Negative: The square of any real number is always non-negative. This means: \[ a^2 \geq 0 \quad \text{for all} \quad a \in \mathbb{R} \]
- Positive and Negative Numbers: The square of both positive and negative numbers is positive: \[ 5^2 = 25 \quad \text{and} \quad (-5)^2 = 25 \]
- Zero: The square of zero is zero: \[ 0^2 = 0 \]
- Growth Rate: Squaring a number increases its magnitude. Larger numbers grow exponentially when squared: \[ 10^2 = 100 \quad \text{and} \quad 100^2 = 10000 \]
- Sum of Squares: The square of the sum of two numbers is equal to the sum of their squares plus twice the product of the two numbers: \[ (a + b)^2 = a^2 + b^2 + 2ab \]
- Difference of Squares: The difference of the squares of two numbers is equal to the product of their sum and difference: \[ a^2 - b^2 = (a + b)(a - b) \]
Let's look at these properties in a tabular format for better understanding:
| Property | Example |
| Always Non-Negative | \[ (-4)^2 = 16 \quad \text{and} \quad 4^2 = 16 \] |
| Zero | \[ 0^2 = 0 \] |
| Growth Rate | \[ 3^2 = 9 \quad \text{and} \quad 30^2 = 900 \] |
| Sum of Squares | \[ (2 + 3)^2 = 2^2 + 3^2 + 2(2 \times 3) = 25 \] |
| Difference of Squares | \[ 5^2 - 3^2 = (5 + 3)(5 - 3) = 16 \] |
Understanding these properties helps in simplifying and solving complex mathematical problems efficiently.
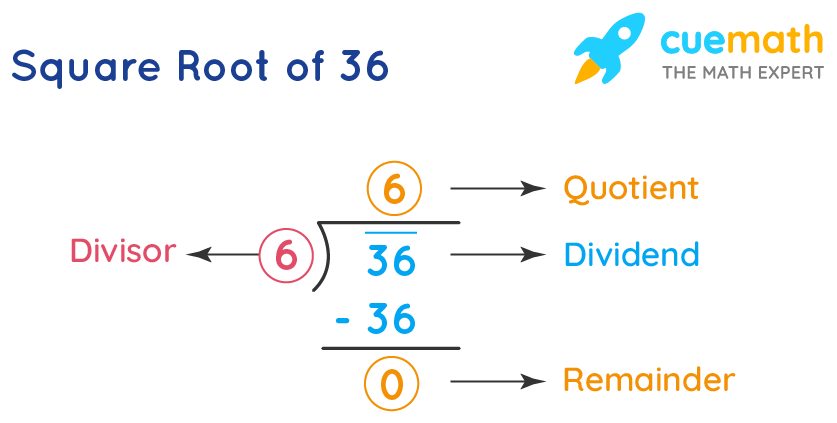
Applications of Squaring in Real Life
Squaring numbers is a fundamental mathematical operation with numerous practical applications in everyday life and various fields of study. Here are some of the key applications:
- Geometry:
- Calculating the area of a square: The area is found by squaring the length of one of its sides. For example, if each side of a square is 36 units, the area is: \[ \text{Area} = 36^2 = 1296 \, \text{square units} \]
- Determining distances: Squaring is used in the Pythagorean theorem to calculate the distance between two points in a plane.
- Physics:
- Calculating kinetic energy: The kinetic energy (\(KE\)) of an object is given by the formula: \[ KE = \frac{1}{2}mv^2 \] where \(m\) is the mass and \(v\) is the velocity of the object. Squaring the velocity is essential for this calculation.
- Determining gravitational force: The inverse square law describes how the force of gravity decreases with the square of the distance between two objects.
- Finance:
- Calculating compound interest: The formula for compound interest involves squaring the growth factor to determine the future value of an investment.
- Statistics:
- Calculating variance: Variance is a measure of the dispersion of a set of data points and is calculated by squaring the differences between each data point and the mean.
- Standard deviation: The standard deviation, a measure of data spread, is derived from the square root of the variance.
Let's illustrate some of these applications in a tabular format:
| Field | Application | Example |
| Geometry | Calculating the area of a square | \[ \text{Area} = 36^2 = 1296 \, \text{square units} \] |
| Physics | Calculating kinetic energy | \[ KE = \frac{1}{2}mv^2 \] |
| Finance | Calculating compound interest | \[ A = P \left(1 + \frac{r}{n}\right)^{nt} \] |
| Statistics | Calculating variance | \[ \sigma^2 = \frac{1}{N}\sum (x_i - \mu)^2 \] |
These examples demonstrate the importance of squaring in various real-life applications, highlighting its value in practical and theoretical contexts.
Visual Representation of Squaring
Visualizing the squaring of numbers can help in understanding the concept better. Let's explore how the square of 36 can be represented visually.
First, consider a square with each side measuring 36 units. The area of this square is calculated by squaring the length of one side:
We can break down this visualization step by step:
- Draw a square with a side length of 36 units.
- Divide the square into smaller squares, each with a side length of 1 unit. This will result in a grid of 36 rows and 36 columns.
- Count the total number of smaller squares within the larger square. This total is the area of the larger square: \[ 36 \times 36 = 1296 \]
Below is a tabular representation to illustrate the breakdown:
| Step | Description | Visualization |
| 1 | Draw a large square with side length 36 units | |
| 2 | Divide the square into a grid of 36x36 smaller squares | |
| 3 | Count the total number of smaller squares (36x36) |
This visual approach to understanding squaring helps to see how multiplying a number by itself forms a larger square, making the concept of squaring more intuitive and concrete.
Comparison with Other Squares
The square of 36, which is 1,296, can be compared with the squares of numbers close to it. Understanding these comparisons helps to grasp the relationships and patterns in squared numbers.
- 31² = 961
- 32² = 1,024
- 33² = 1,089
- 34² = 1,156
- 35² = 1,225
- 36² = 1,296
- 37² = 1,369
- 38² = 1,444
- 39² = 1,521
- 40² = 1,600
- 41² = 1,681
From the table above, it is clear that as numbers increase, their squares grow significantly. For instance, the difference between the squares of 36 and 35 is:
This can also be expressed as:
where \(n\) is 35 in this case. Thus:
Comparing even and odd squares, the pattern is consistent. The squares of even numbers are always even, and the squares of odd numbers are always odd:
- Even squares: 32² = 1,024, 34² = 1,156, 36² = 1,296
- Odd squares: 31² = 961, 33² = 1,089, 35² = 1,225
Squares also appear diagonally in multiplication charts, showcasing their unique properties. For example, the square numbers of the first ten integers are:
- 1² = 1
- 2² = 4
- 3² = 9
- 4² = 16
- 5² = 25
- 6² = 36
- 7² = 49
- 8² = 64
- 9² = 81
- 10² = 100
Observing these patterns and relationships helps in understanding the behavior of square numbers and their significance in mathematics.
Common Mistakes in Squaring Numbers
When squaring numbers, especially in mathematical calculations and educational contexts, certain common mistakes can arise. Understanding these errors can help improve accuracy and confidence in performing squaring operations.
- Incorrect Formula Usage: A frequent mistake is using the wrong formula for squaring. For instance, instead of squaring the number correctly, individuals may use a multiplication formula incorrectly. The correct formula for squaring a number x is \( x^2 \), which means \( x \times x \).
- Forgetting Negative Signs: Another common error is forgetting to consider the negative sign when squaring negative numbers. For example, when squaring -5, the correct result is \( (-5) \times (-5) = 25 \). Ignoring the negative sign can lead to incorrect results.
- Order of Operations Mistakes: Mistakes often occur when the order of operations (PEMDAS/BODMAS) is not followed correctly. It's essential to perform exponentiation before any addition or subtraction in a complex expression.
- Misunderstanding Squaring of Fractions and Decimals: Squaring fractions and decimals can be tricky. For instance, \( \left( \frac{1}{2} \right)^2 \) is \( \frac{1}{4} \), not \( \frac{1}{2} \). Similarly, \( (0.5)^2 = 0.25 \), not 0.5.
- Calculator Input Errors: When using calculators, inputting the numbers incorrectly or pressing the wrong keys can lead to mistakes. Double-checking the entered values is crucial to avoid such errors.
To minimize these common mistakes, always ensure that:
- You use the correct formula and notation.
- Negative signs are appropriately accounted for.
- The order of operations is followed meticulously.
- Care is taken when squaring fractions and decimals.
- Calculator inputs are checked for accuracy.
By being aware of these potential pitfalls, you can improve your accuracy and confidence when squaring numbers.

Practice Problems and Examples
Practicing squaring numbers is essential for mastering this mathematical concept. Below are several problems and examples to help you understand and apply the concept of squaring numbers.
Example 1: Basic Squaring
Find the square of 7.
Solution: \( 7^2 = 7 \times 7 = 49 \)
Example 2: Squaring Larger Numbers
Find the square of 25.
Solution: \( 25^2 = 25 \times 25 = 625 \)
Example 3: Squaring Negative Numbers
Find the square of -8.
Solution: \( (-8)^2 = (-8) \times (-8) = 64 \)
Practice Problems
- Calculate the square of 15.
- What is \( (-6)^2 \)?
- Find the square of 12.
- Calculate \( 20^2 \).
- What is the square of 11?
Step-by-Step Solutions
Problem 1: Calculate the square of 15.
Solution: \( 15^2 = 15 \times 15 = 225 \)
Problem 2: What is \( (-6)^2 \)?
Solution: \( (-6)^2 = (-6) \times (-6) = 36 \)
Problem 3: Find the square of 12.
Solution: \( 12^2 = 12 \times 12 = 144 \)
Problem 4: Calculate \( 20^2 \).
Solution: \( 20^2 = 20 \times 20 = 400 \)
Problem 5: What is the square of 11?
Solution: \( 11^2 = 11 \times 11 = 121 \)
Additional Practice Problems
- Calculate \( 18^2 \).
- What is \( (-9)^2 \)?
- Find the square of 22.
- Calculate \( 30^2 \).
- What is the square of 13?
Advanced Problems
For those looking for more challenging problems, try these:
- Find the square of 52.
- What is \( (-24)^2 \)?
- Calculate \( 37^2 \) without using a calculator.
- Find the square of 99.
- What is the square of 65?
Advanced Problem Solutions
Problem 1: Find the square of 52.
Solution: \( 52^2 = 52 \times 52 = 2704 \)
Problem 2: What is \( (-24)^2 \)?
Solution: \( (-24)^2 = (-24) \times (-24) = 576 \)
Problem 3: Calculate \( 37^2 \) without using a calculator.
Solution: \( 37^2 = 37 \times 37 = 1369 \)
Problem 4: Find the square of 99.
Solution: \( 99^2 = 99 \times 99 = 9801 \)
Problem 5: What is the square of 65?
Solution: \( 65^2 = 65 \times 65 = 4225 \)
Conclusion
The square of 36 is a fundamental example of squaring numbers, which is an important concept in mathematics. Squaring a number involves multiplying the number by itself, and in this case, \( 36^2 = 36 \times 36 = 1,296 \). Understanding how to calculate squares and recognizing the patterns in squared numbers can aid in various mathematical applications and problem-solving scenarios.
To summarize:
- Squaring a number means multiplying it by itself.
- The square of 36 is \( 1,296 \).
- Squaring numbers can be applied in geometry, algebra, and various real-life situations.
- Common mistakes in squaring numbers include incorrect formula usage, forgetting negative signs, and calculator input errors.
- Practice problems help in mastering the concept of squaring numbers and avoiding common errors.
By understanding and practicing the concept of squaring numbers, you can enhance your mathematical skills and confidence. Remember, the more you practice, the more proficient you will become in performing these calculations accurately and efficiently.
We hope this guide has provided you with a clear understanding of squaring numbers and the importance of this mathematical operation. Continue practicing, and soon you will master the concept of squaring numbers effortlessly.
Video giải thích tại sao căn bậc hai của 36 chỉ là 6 dương. Khám phá toán học và những khái niệm quan trọng liên quan đến căn bậc hai.
Tại sao căn bậc hai của 36 chỉ là 6 dương
READ MORE:
Video giải thích về căn bậc hai của 36. Tìm hiểu cách tính và ý nghĩa của căn bậc hai trong toán học.
Căn Bậc Hai của 36