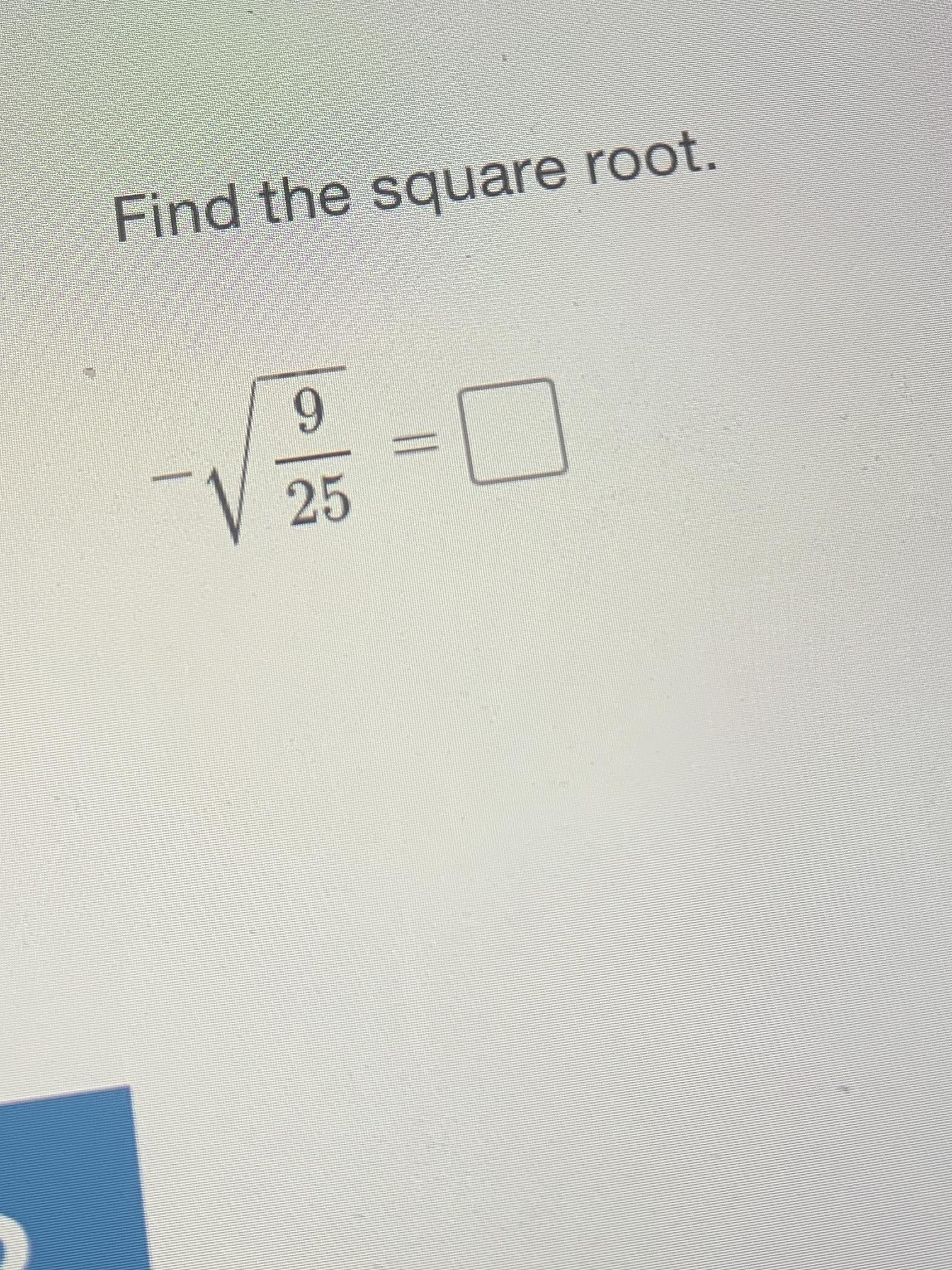
Topic how to find the square root of 225: Discover the easiest and most effective methods to find the square root of 225. This guide will walk you through step-by-step instructions using prime factorization, long division, and calculators, ensuring you grasp each method with ease. Whether you're a student or just curious, learn how to master square roots today!
Table of Content
- How to Find the Square Root of 225
- Introduction to Square Roots
- Definition and Importance of Square Roots
- Methods to Calculate Square Roots
- Using Prime Factorization
- Steps for Prime Factorization
- Examples of Prime Factorization
- Using Long Division Method
- Steps for Long Division Method
- Examples of Long Division Method
- Using a Calculator
- Steps to Use a Calculator for Square Roots
- Comparing Different Methods
- Advantages and Disadvantages of Each Method
- Applications of Square Roots in Real Life
- Practice Problems and Solutions
- YOUTUBE: Hướng dẫn chi tiết cách tìm căn bậc hai của 225 bằng phương pháp phân tích thừa số nguyên tố. Cùng khám phá và học cách tính căn bậc hai một cách dễ hiểu.
How to Find the Square Root of 225
The square root of a number is a value that, when multiplied by itself, gives the original number. To find the square root of 225, we can use several methods including prime factorization, long division, and using a calculator. Below are detailed explanations of these methods:
1. Using Prime Factorization
- Find the prime factors of 225:
- 225 is divisible by 3 (since the sum of the digits \(2 + 2 + 5 = 9\), which is divisible by 3)
- \(225 \div 3 = 75\)
- 75 is also divisible by 3 (since \(7 + 5 = 12\), which is divisible by 3)
- \(75 \div 3 = 25\)
- 25 is divisible by 5
- \(25 \div 5 = 5\)
- \(5 \div 5 = 1\)
- Prime factors of 225 are \(3 \times 3 \times 5 \times 5\)
- Group the prime factors into pairs of equal factors: \((3 \times 3) \) and \((5 \times 5)\)
- The square root of each pair is \(3\) and \(5\)
- Multiply the results: \(3 \times 5 = 15\)
- Therefore, \(\sqrt{225} = 15\)
2. Using Long Division Method
- Pair the digits of 225 from right to left: \(2 | 25\)
- Find the largest number whose square is less than or equal to 2. This number is 1 (\(1^2 = 1\))
- Subtract \(1^2\) from 2: \(2 - 1 = 1\)
- Bring down the next pair of digits (25), making it 125
- Double the number obtained in the quotient (1), making it 2
- Find a digit (X) such that \(20X \times X\) is less than or equal to 125. This digit is 5 (\(205 \times 5 = 1025\))
- Place the 5 in the quotient: \(15\)
- Subtract \(1025\) from 125: \(125 - 1025 = 0\)
3. Using a Calculator
- Turn on the calculator
- Enter 225
- Press the square root (√) button
- The calculator will display 15
Conclusion
By using any of the methods above, we can determine that the square root of 225 is 15.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is a fundamental concept in mathematics with widespread applications. Understanding square roots is essential for solving various mathematical problems, from basic arithmetic to advanced algebra and geometry.
For example, the square root of 225 is written as \( \sqrt{225} \). Since \( 15 \times 15 = 225 \), \( \sqrt{225} = 15 \).
There are several methods to find the square root of a number, including:
- Prime Factorization
- Long Division Method
- Using a Calculator
Each method offers a different approach and can be useful in various situations. In the following sections, we will explore each method in detail, providing step-by-step instructions to help you master the concept of square roots.
Definition and Importance of Square Roots
Square roots are mathematical operations that determine a value which, when multiplied by itself, equals the original number. Symbolically, the square root of a number \( x \) is represented as \( \sqrt{x} \). For example, \( \sqrt{225} = 15 \) because \( 15 \times 15 = 225 \).
Understanding square roots is crucial for several reasons:
- Fundamental Mathematical Concept: Square roots are a basic component of arithmetic, essential for learning advanced mathematical topics such as algebra, calculus, and geometry.
- Solving Equations: Square roots are used to solve quadratic equations, which appear frequently in various branches of mathematics and science.
- Geometry and Measurement: Square roots help in calculating distances, areas, and volumes, making them vital for fields like architecture, engineering, and physics.
- Data Analysis: In statistics, square roots are used in standard deviation calculations and other measures of spread, which are important for data interpretation.
- Real-life Applications: Square roots are applied in various real-world situations, such as computing interest rates, analyzing scientific data, and optimizing processes in technology and business.
By mastering the concept of square roots, you gain a powerful tool that enhances your problem-solving abilities and broadens your understanding of the world around you. In the next sections, we will delve into specific methods for calculating square roots, using the example of finding \( \sqrt{225} \).
Methods to Calculate Square Roots
Finding the square root of a number can be approached in several ways. Here, we will explore three primary methods: Prime Factorization, Long Division Method, and using a Calculator. Each method has its own steps and can be applied depending on the context and tools available.
Prime Factorization Method
- Factorize the number into its prime factors:
- 225 can be broken down into \( 225 = 3 \times 3 \times 5 \times 5 \).
- Group the prime factors into pairs:
- \( (3 \times 3) \) and \( (5 \times 5) \).
- Take the square root of each pair:
- \( \sqrt{3 \times 3} = 3 \)
- \( \sqrt{5 \times 5} = 5 \)
- Multiply the results of each pair:
- \( 3 \times 5 = 15 \)
- Thus, \( \sqrt{225} = 15 \).
Long Division Method
- Pair the digits of the number from right to left:
- \( 225 \) becomes \( 2 \, | \, 25 \).
- Find the largest number whose square is less than or equal to the first pair (2):
- The largest number is 1 (\( 1^2 = 1 \)).
- Subtract the square of this number from the first pair:
- \( 2 - 1 = 1 \).
- Bring down the next pair of digits (25), making it 125.
- Double the number obtained in the quotient (1), making it 2.
- Find a digit (X) such that \( 20X \times X \) is less than or equal to 125:
- This digit is 5 (\( 205 \times 5 = 1025 \)).
- Place the 5 in the quotient, giving you 15.
- Therefore, \( \sqrt{225} = 15 \).
Using a Calculator
- Turn on the calculator.
- Enter the number 225.
- Press the square root (√) button.
- The calculator will display 15.
- Thus, \( \sqrt{225} = 15 \).
Each of these methods provides a reliable way to find the square root of a number. Whether you prefer manual calculation or using a calculator, understanding these methods will enhance your mathematical skills and problem-solving abilities.
Using Prime Factorization
Prime factorization is a method of expressing a number as the product of its prime factors. This method can be used to find the square root of a number by identifying pairs of prime factors. Here is a detailed step-by-step process to find the square root of 225 using prime factorization:
- Start by finding the prime factors of 225:
- 225 is an odd number, so it is not divisible by 2.
- The sum of the digits (2 + 2 + 5 = 9) is divisible by 3, so 225 is divisible by 3.
- \(225 \div 3 = 75\).
- 75 is also divisible by 3 (since 7 + 5 = 12, and 12 is divisible by 3).
- \(75 \div 3 = 25\).
- 25 is divisible by 5 (since it ends in 5).
- \(25 \div 5 = 5\).
- Finally, 5 is a prime number.
- Write 225 as a product of its prime factors:
- \(225 = 3 \times 3 \times 5 \times 5\).
- Group the prime factors into pairs:
- \((3 \times 3)\) and \((5 \times 5)\).
- Take the square root of each pair:
- \(\sqrt{3 \times 3} = 3\)
- \(\sqrt{5 \times 5} = 5\)
- Multiply the results of the square roots:
- \(3 \times 5 = 15\)
- Therefore, the square root of 225 is:
- \(\sqrt{225} = 15\).
Using prime factorization to find the square root of 225 shows a clear and structured approach, making it easier to understand the concept of square roots and their calculations.

Steps for Prime Factorization
Prime factorization is a method of breaking down a number into its basic prime factors. This technique can be particularly useful for finding the square root of a number. Here are the detailed steps to perform prime factorization on 225:
- Identify the smallest prime number that divides 225:
- 225 is odd, so it is not divisible by 2.
- Check divisibility by 3: The sum of the digits of 225 (2 + 2 + 5 = 9) is divisible by 3.
- Divide 225 by 3:
- \(225 \div 3 = 75\).
- Repeat the process with 75:
- 75 is also divisible by 3 (7 + 5 = 12, and 12 is divisible by 3).
- \(75 \div 3 = 25\).
- Continue with 25:
- 25 ends in 5, so it is divisible by 5.
- \(25 \div 5 = 5\).
- 5 is a prime number.
- Write 225 as a product of its prime factors:
- \(225 = 3 \times 3 \times 5 \times 5\).
- Group the prime factors into pairs:
- \((3 \times 3)\) and \((5 \times 5)\).
- Take the square root of each pair:
- \(\sqrt{3 \times 3} = 3\)
- \(\sqrt{5 \times 5} = 5\)
- Multiply the results of the square roots:
- \(3 \times 5 = 15\)
- Therefore, the square root of 225 is:
- \(\sqrt{225} = 15\).
Prime factorization is a clear and systematic way to find the square root of a number, helping to understand the underlying mathematical principles.
Examples of Prime Factorization
Prime factorization is a method used to express a number as a product of its prime factors. To find the square root of a number using prime factorization, we break down the number into its prime factors and then pair them appropriately. Let's consider the example of finding the square root of 225 using prime factorization.
Steps to find the square root of 225 using prime factorization:
First, we find the prime factors of 225:
- 225 is divisible by 3 (the smallest prime number that divides 225).
- 225 ÷ 3 = 75
- 75 is also divisible by 3.
- 75 ÷ 3 = 25
- 25 is divisible by 5 (the smallest prime number that divides 25).
- 25 ÷ 5 = 5
- 5 is a prime number.
So, the prime factorization of 225 is: 225 = 3 × 3 × 5 × 5.
Next, we write the prime factorization in exponential form:
225 = 32 × 52
To find the square root, we take the square root of each factor:
√225 = √(32 × 52)
We can simplify this by taking the square root of each prime factor pair:
√225 = √(32) × √(52)
The square root of a squared number is the number itself:
√(32) = 3 and √(52) = 5
Therefore:
√225 = 3 × 5 = 15
Hence, the square root of 225 is 15.
Let's look at another example:
Find the square root of 144 using prime factorization:
- Prime factorize 144:
- 144 is divisible by 2 (the smallest prime number that divides 144).
- 144 ÷ 2 = 72
- 72 is divisible by 2.
- 72 ÷ 2 = 36
- 36 is divisible by 2.
- 36 ÷ 2 = 18
- 18 is divisible by 2.
- 18 ÷ 2 = 9
- 9 is divisible by 3.
- 9 ÷ 3 = 3
- 3 is a prime number.
So, the prime factorization of 144 is: 144 = 2 × 2 × 2 × 2 × 3 × 3.
- Write the prime factorization in exponential form:
144 = 24 × 32
- Find the square root of each factor:
√144 = √(24 × 32)
- Simplify by taking the square root of each prime factor pair:
√144 = √(24) × √(32)
- The square root of a squared number is the number itself:
√(24) = 22 = 4 and √(32) = 3
- Therefore:
√144 = 4 × 3 = 12
Hence, the square root of 144 is 12.
Using Long Division Method
The long division method is a systematic technique to find the square root of a number. Here is a detailed step-by-step process to find the square root of 225 using the long division method:
- Set up the number:
Write the number 225 under the long division symbol.
- Pair the digits:
Starting from the right, pair the digits of 225. So, we have 2 and 25.
- Find the largest number:
Find the largest number whose square is less than or equal to the first pair (or single digit if it is not a pair). In this case, the largest number whose square is less than or equal to 2 is 1 (1x1=1).
- Write 1 as the quotient, and subtract 12 (which is 1) from 2, leaving a remainder of 1.
- Bring down the next pair:
Bring down the next pair of digits (25) next to the remainder, making the new dividend 125.
- Double the quotient:
Double the current quotient (which is 1), giving us 2. This is the first digit of our new divisor.
- Find the next digit:
Find a digit (let's call it X) such that when 2X is multiplied by X, the product is less than or equal to 125. The number 5 works because 25 x 5 = 125.
- Write 5 next to 2, making the new divisor 25.
- Write 5 next to 1 in the quotient.
- Subtract and repeat:
Subtract 125 from 125, leaving a remainder of 0. Since we have no more digits to bring down and the remainder is 0, the quotient is 15.
Thus, the square root of 225 using the long division method is 15.
| Step | Action | Dividend | Quotient | Divisor | Remainder |
|---|---|---|---|---|---|
| 1 | Initial Setup | 225 | |||
| 2 | Pair digits | 2 | 25 | |||
| 3 | Find largest square | 2 | 25 | 1 | 1 | 1 |
| 4 | Bring down next pair | 125 | 1 | 1 | |
| 5 | Double quotient | 125 | 1 | 2 | |
| 6 | Find next digit | 125 | 15 | 25 | 0 |
Steps for Long Division Method
The long division method for finding the square root of 225 involves the following steps:
- Pair the Digits: Start by writing 225 and pairing the digits from right to left. Here, we have the pair (25) and the single digit (2).
- Find the Largest Number: Determine the largest number whose square is less than or equal to 2. In this case, it is 1, since \(1^2 = 1\).
- Divide and Subtract: Place 1 as the first digit of the quotient. Subtract \(1^2 = 1\) from 2, leaving a remainder of 1.
- Bring Down the Next Pair: Bring down the next pair of digits (25) to the right of the remainder. The new number to be divided is 125.
- Double the Quotient: Double the current quotient (1), giving 2, and place it as the starting digit of the new divisor.
- Find the Next Digit: Find a digit \(X\) such that 2X multiplied by X is less than or equal to 125. The correct digit is 5, because \(25 \times 5 = 125\).
- Complete the Division: Place 5 next to 2 to form 25, then multiply 25 by 5 to get 125. Subtract 125 from 125, leaving a remainder of 0.
The quotient, which is 15, is the square root of 225.
Thus, using the long division method, the square root of 225 is found to be 15.

Examples of Long Division Method
To find the square root of 225 using the long division method, follow these steps:
-
Pair the digits of 225 from right to left. In this case, 225 becomes 2 | 25.
-
Find the largest number whose square is less than or equal to the first pair. The largest number whose square is less than or equal to 2 is 1 (since \(1^2 = 1\)).
-
Place the quotient (1) above the first pair (2), and subtract \(1^2 = 1\) from 2. The remainder is 1.
-
Bring down the next pair (25) to the right of the remainder, making the new dividend 125.
-
Double the quotient (1) and write it next to the new dividend, leaving a blank space for the next digit. This makes the new divisor 20_. Find a digit for the blank space such that \(20_ \times _ \leq 125\). The digit 5 works because \(205 \times 5 = 1025\) is less than or equal to 125.
-
Place the 5 in the blank space and also in the quotient. Subtract 105 from 125 to get a remainder of 20. Bring down the next digit (which is 0 in this case, so we are done).
-
The quotient is 15, so the square root of 225 is 15.
This method shows that the square root of 225 is indeed 15, demonstrating the accuracy and reliability of the long division method.
Using a Calculator
Finding the square root of 225 using a calculator is a quick and easy method. Here are the steps to follow:
- Turn on your calculator.
- Locate the square root button. It is usually represented by the symbol √.
- Press the square root button.
- Enter the number 225.
- Press the equals (=) button to get the result.
The display will show 15, which is the square root of 225.
Using a calculator ensures you get an accurate result quickly and is especially useful for larger numbers or for checking your work from manual calculations.
Here is a simple HTML table to illustrate the process:
| Step | Action | Button Press | Display |
|---|---|---|---|
| 1 | Turn on calculator | On | 0 |
| 2 | Select square root function | √ | √ |
| 3 | Enter the number | 225 | √225 |
| 4 | Compute the result | = | 15 |
This method is straightforward and minimizes the risk of errors, making it ideal for students and professionals alike.
Steps to Use a Calculator for Square Roots
Using a calculator to find the square root of a number is a straightforward process. Here are the steps to follow:
-
Turn on your calculator and clear any previous calculations by pressing the "C" or "AC" button.
-
Locate the square root button (√) on your calculator. This button is usually above one of the number keys, and you might need to press the "Shift" or "2nd" key to access it.
-
Enter the number for which you want to find the square root. In this case, enter 225.
-
Press the square root button (√). On some calculators, you might need to enter the number first and then press the square root button, while on others, you press the square root button and then enter the number.
-
Read the result displayed on the calculator screen. For 225, the result should be 15.
Here is an example using a calculator:
- Step 1: Turn on the calculator.
- Step 2: Press the "C" or "AC" button to clear any previous input.
- Step 3: Press "225".
- Step 4: Press the "√" button.
- Step 5: The display will show "15".
Using a calculator is the quickest and most accurate method for finding square roots, especially for large or non-perfect square numbers.
Comparing Different Methods
Finding the square root of 225 can be approached through various methods, each with its own advantages and disadvantages. Here, we compare the prime factorization method, the long division method, and using a calculator.
Prime Factorization Method
- Steps:
- Express 225 as a product of its prime factors: \(225 = 3 \times 3 \times 5 \times 5\).
- Group the prime factors into pairs: \(225 = (3 \times 3) \times (5 \times 5)\).
- Take the square root of each pair: \(\sqrt{225} = \sqrt{(3 \times 3) \times (5 \times 5)} = 3 \times 5 = 15\).
- Advantages:
- Straightforward for perfect squares.
- Helps in understanding the factorization of numbers.
- Disadvantages:
- Not efficient for large numbers or numbers that are not perfect squares.
Long Division Method
- Steps:
- Pair the digits of the number starting from the right: \(2|25\).
- Find the largest number whose square is less than or equal to the first pair (2): 1.
- Subtract and bring down the next pair: \(2-1^2 = 1\), bring down 25 to get 125.
- Double the current quotient (1) to get the new divisor (2) and find the next digit (5): \(25 \times 5 = 125\).
- Continue the process until the remainder is 0. The quotient is 15.
- Advantages:
- Works for both perfect and non-perfect squares.
- Provides a systematic approach to finding square roots.
- Disadvantages:
- Time-consuming and complex for large numbers.
- Requires more steps and careful calculations.
Using a Calculator
- Steps:
- Turn on the calculator.
- Enter the number 225.
- Press the square root (√) button.
- Read the result displayed: 15.
- Advantages:
- Quick and easy.
- Accurate for all numbers, including large ones and non-perfect squares.
- Disadvantages:
- Does not help in understanding the underlying mathematical process.
- Requires access to a calculator.
Each method has its specific use cases and is valuable depending on the context. Prime factorization is excellent for learning and understanding number properties, the long division method is comprehensive and works for all numbers, and using a calculator is the most efficient for quick and accurate results.
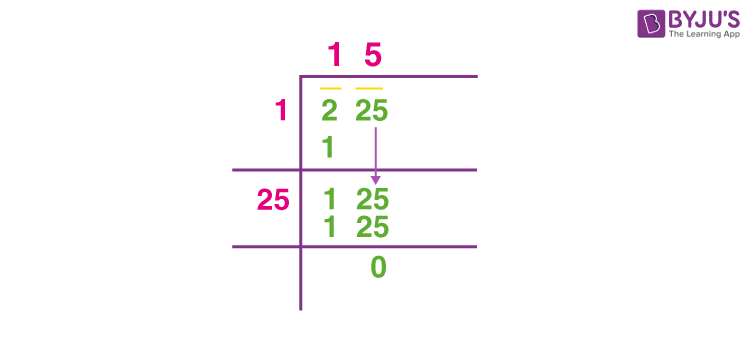
Advantages and Disadvantages of Each Method
When calculating the square root of 225, several methods can be used. Each method has its advantages and disadvantages:
Prime Factorization
- Advantages:
- Simplicity: The steps are straightforward and easy to follow.
- Educational: It helps in understanding the fundamental principles of prime numbers and factorization.
- Disadvantages:
- Time-Consuming: Can be lengthy for larger numbers with many prime factors.
- Not Practical for Non-Perfect Squares: This method is less effective for numbers that are not perfect squares.
Long Division Method
- Advantages:
- Accuracy: Provides an exact value for the square root.
- Universality: Works for any positive number, including non-perfect squares.
- Disadvantages:
- Complexity: Involves multiple steps and can be difficult to master.
- Time-Consuming: Takes longer compared to using a calculator.
Using a Calculator
- Advantages:
- Speed: Quick and efficient, providing instant results.
- Ease of Use: Simple to use, requiring minimal steps.
- Disadvantages:
- Dependence: Requires access to a calculator, which might not always be available.
- Limited Learning: Does not help in understanding the underlying mathematical concepts.
Repeated Subtraction Method
- Advantages:
- Conceptual Understanding: Enhances comprehension of the relationship between squares and square roots.
- Simple Arithmetic: Uses basic subtraction, making it accessible for beginners.
- Disadvantages:
- Impractical for Large Numbers: Becomes cumbersome and impractical for larger numbers.
- Not Efficient: More time-consuming compared to other methods.
Applications of Square Roots in Real Life
Square roots have various applications in real-life scenarios. Here are some notable examples:
-
Finance:
In finance, square roots are used to calculate stock market volatility, which measures the price fluctuations of stocks. This helps investors assess the risk of investments by taking the square root of the variance in stock returns.
-
Architecture and Engineering:
Architects and engineers use square roots to determine the natural frequencies of structures like bridges and buildings. This helps in predicting how structures will respond to different loads, such as wind or traffic.
-
Science:
Square roots are used in various scientific calculations, such as determining the velocity of an object, the intensity of sound waves, and the amount of radiation absorbed by materials. These calculations help scientists understand natural phenomena and develop new technologies.
-
Statistics:
In statistics, square roots are essential for calculating standard deviation, which measures the dispersion of a data set. The standard deviation is the square root of the variance and is used to analyze and interpret data.
-
Geometry:
Geometry often involves square roots to calculate the area and perimeter of shapes, as well as to solve problems related to right triangles using the Pythagorean theorem.
-
Computer Science:
Square roots are used in computer programming for algorithms related to encryption, image processing, and game physics. For instance, encryption algorithms use square roots to generate secure keys for data transmission.
-
Navigation:
Square roots are used in navigation to compute distances and directions between points on a map. Pilots, for example, use square roots to calculate the distance between two points on a flight path.
-
Electrical Engineering:
In electrical engineering, square roots are used to compute power, voltage, and current in circuits, which is crucial for designing electrical systems like power grids and electronic devices.
-
Photography:
In photography, the aperture of a camera lens is controlled using f-numbers, which are proportional to the square root of the light entering the camera. This helps in adjusting the exposure of photographs.
-
Accident Investigation:
Police officers use square roots to determine the speed of a vehicle before an accident by measuring the length of skid marks. This involves applying formulas that use the square root of the skid distance to estimate speed.
Practice Problems and Solutions
To reinforce your understanding of finding square roots, here are some practice problems along with their solutions. These examples use various methods such as prime factorization and the long division method.
Problem 1: Find the square root of 225 using Prime Factorization
- Prime factorize 225: \(225 = 3 \times 3 \times 5 \times 5\)
- Group the prime factors into pairs: \((3 \times 3) \times (5 \times 5)\)
- Take one number from each pair: \(3 \times 5 = 15\)
So, the square root of 225 is \(15\).
Problem 2: Find the square root of 144 using Prime Factorization
- Prime factorize 144: \(144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3\)
- Group the prime factors into pairs: \((2 \times 2) \times (2 \times 2) \times (3 \times 3)\)
- Take one number from each pair: \(2 \times 2 \times 3 = 12\)
So, the square root of 144 is \(12\).
Problem 3: Find the square root of 225 using the Long Division Method
- Pair the digits from right: \(\overline{2} \ \overline{25}\)
- Find the largest number whose square is less than or equal to the first pair: \(1 \times 1 = 1\)
- Subtract and bring down the next pair: \(2 - 1 = 1\), bring down 25, making 125
- Double the quotient: \(1 \times 2 = 2\)
- Find the number \(x\) such that \(20x \times x \leq 125\): \(25 \times 5 = 125\)
- The quotient is 15 and the remainder is 0
So, the square root of 225 is \(15\).
Problem 4: Find the square root of 400 using Prime Factorization
- Prime factorize 400: \(400 = 2 \times 2 \times 2 \times 2 \times 5 \times 5\)
- Group the prime factors into pairs: \((2 \times 2) \times (2 \times 2) \times (5 \times 5)\)
- Take one number from each pair: \(2 \times 2 \times 5 = 20\)
So, the square root of 400 is \(20\).
Additional Practice Problems
- Find the square root of 64.
- Estimate the square root of 441.
- Find the value of \(\sqrt{20} + \sqrt{144}\).
Work through these problems using the methods described above. The answers are 8, 21, and 14 respectively.
Hướng dẫn chi tiết cách tìm căn bậc hai của 225 bằng phương pháp phân tích thừa số nguyên tố. Cùng khám phá và học cách tính căn bậc hai một cách dễ hiểu.
Cách Tìm Căn Bậc Hai của 225 Bằng Phân Tích Thừa Số Nguyên Tố / Căn Bậc Hai của 225 / 225 Căn Bậc Hai
READ MORE:
Hướng dẫn cách tìm căn bậc hai của các số 225, 256, 20 và 40 mà không cần dùng máy tính. Khám phá phương pháp tính toán chi tiết và dễ hiểu.
Tìm Căn Bậc Hai của 225, 256, 20 và Căn Bậc Hai của 40 Không Cần Máy Tính