Topic what is the square root of 21: The square root of 21 is a captivating mathematical concept that reveals much about numbers and their properties. In this article, we delve into the significance, calculation methods, and intriguing facts surrounding \( \sqrt{21} \). Join us as we explore why this irrational number holds such an important place in mathematics.
Table of Content
- Square Root of 21
- Introduction
- Definition of Square Root
- Understanding Square Roots
- Mathematical Representation
- Calculation Methods
- Decimal Approximation
- Prime Factorization
- Irrational Numbers
- Properties of Square Root of 21
- Applications in Mathematics
- Real-Life Applications
- Common Misconceptions
- Visual Representation
- Historical Context
- Advanced Topics
- Conclusion
- YOUTUBE: Khám phá cách tính căn bậc hai của 21 và ứng dụng trong cuộc sống với video hướng dẫn chi tiết bằng tiếng Việt.
Square Root of 21
The square root of 21 is a value that, when multiplied by itself, gives the number 21. It is represented mathematically as \( \sqrt{21} \).
Decimal Form
The square root of 21 in decimal form is approximately:
\( \sqrt{21} \approx 4.58257569495584 \)
Irrational Number
The square root of 21 is an irrational number, which means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Prime Factorization Method
The prime factorization method for finding square roots involves expressing the number as a product of prime numbers. However, 21 is already factored as:
\( 21 = 3 \times 7 \)
Since neither 3 nor 7 are perfect squares, the square root of 21 is not a simple rational number.
Symbolic Representation
In mathematical notation, the square root of 21 is represented as:
\( \sqrt{21} \)
Table of Approximations
Here is a table with some approximations of the square root of 21:
| Decimal Places | Value |
| 1 | 4.6 |
| 2 | 4.58 |
| 3 | 4.583 |
| 4 | 4.5826 |
| 5 | 4.58258 |
Applications
The square root of 21 can be used in various mathematical calculations and applications, particularly in geometry and algebra where exact square roots are needed.

READ MORE:
Introduction
The square root of 21, denoted as \( \sqrt{21} \), is an intriguing mathematical concept with various applications and properties. Understanding square roots helps in grasping the nature of numbers and their relationships. This section provides a comprehensive overview of the square root of 21, including its calculation, properties, and significance.
Let's break it down step by step:
- Definition: The square root of a number \( x \) is a value that, when multiplied by itself, equals \( x \). For 21, the square root is the number \( y \) such that \( y \times y = 21 \).
- Decimal Approximation: The square root of 21 is an irrational number, approximately equal to 4.5826. This means it cannot be expressed as a simple fraction and its decimal representation is non-repeating and infinite.
- Prime Factorization: The prime factors of 21 are 3 and 7. While this does not directly help in simplifying \( \sqrt{21} \), it highlights that 21 is a product of these prime numbers.
- Properties:
- \( \sqrt{21} \) is an irrational number.
- It lies between the integers 4 and 5.
- It can be approximated to any desired level of accuracy for practical purposes.
- Applications: Understanding and calculating square roots is fundamental in various fields such as geometry, algebra, engineering, and physics. For example, it is essential in solving quadratic equations and in determining distances in coordinate geometry.
By exploring the square root of 21, we gain deeper insights into the properties of irrational numbers and their role in mathematics.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is one of the fundamental operations in mathematics and is denoted by the radical symbol \( \sqrt{} \). The square root of a number \( x \) is written as \( \sqrt{x} \).
For example, to find the square root of 21, we are looking for a number \( y \) such that:
\( y \times y = 21 \)
This can be broken down into the following steps:
- Identify the number: We start with the number 21.
- Determine the square root: The square root of 21 is the number that, when squared, equals 21. This number is approximately 4.5826.
- Symbolic representation: The square root of 21 is represented as \( \sqrt{21} \).
Key properties of square roots include:
- Non-negative results: The principal square root of a non-negative number is also non-negative. Thus, \( \sqrt{21} \approx 4.5826 \) is positive.
- Irrational numbers: The square root of a non-perfect square (like 21) is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form is infinite and non-repeating.
- Inverse operation: Finding the square root is the inverse operation of squaring a number. For instance, since \( 4.5826^2 \approx 21 \), \( \sqrt{21} \approx 4.5826 \).
Understanding square roots is crucial in various mathematical contexts, including solving equations, understanding geometric relationships, and in various real-life applications such as physics and engineering.
Understanding Square Roots
Square roots are fundamental in mathematics and understanding them helps in various fields such as algebra, geometry, and calculus. A square root of a number is a value that, when multiplied by itself, results in the original number. The notation for the square root of a number \( x \) is \( \sqrt{x} \).
To fully grasp square roots, let's explore their properties and how they are calculated:
- Basic Concept:
If \( y \) is the square root of \( x \), then \( y^2 = x \). For instance, the square root of 21, denoted as \( \sqrt{21} \), satisfies \( (\sqrt{21})^2 = 21 \).
- Square Root of Perfect Squares:
Perfect squares are numbers like 1, 4, 9, 16, etc., whose square roots are whole numbers. For example, \( \sqrt{16} = 4 \) because \( 4^2 = 16 \). However, 21 is not a perfect square.
- Square Root of Non-Perfect Squares:
Non-perfect squares like 21 have irrational square roots, meaning their decimal representation is non-terminating and non-repeating. The square root of 21 is approximately 4.5826.
- Approximation Methods:
- Long Division Method: A manual method for approximating square roots by dividing the number into pairs of digits.
- Using a Calculator: Most modern calculators can compute the square root of a number directly.
- Properties of Square Roots:
- Non-negative: The principal square root of a non-negative number is also non-negative. For example, \( \sqrt{21} \) is approximately 4.5826, not -4.5826.
- Multiplication: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). For example, \( \sqrt{4 \times 21} = \sqrt{84} \).
- Division: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{21}{4}} = \frac{\sqrt{21}}{2} \).
- Geometric Interpretation:
In geometry, the square root can represent the length of the side of a square with a given area. For instance, if a square has an area of 21 square units, each side length is \( \sqrt{21} \) units.
By understanding square roots, we can solve quadratic equations, determine distances in coordinate geometry, and perform various mathematical operations that are essential in both theoretical and applied mathematics.
Mathematical Representation
The square root of a number is a fundamental concept in mathematics, often represented using the radical symbol \( \sqrt{} \). The square root of 21 can be mathematically represented and understood through various expressions and methods. Below are detailed steps to represent and approximate the square root of 21.
- Radical Notation:
The most common way to represent the square root of 21 is using the radical symbol:
\( \sqrt{21} \)
- Exponent Notation:
The square root can also be expressed as an exponent. The square root of 21 is written as:
\( 21^{\frac{1}{2}} \)
- Decimal Approximation:
Since 21 is not a perfect square, its square root is an irrational number. The decimal approximation of the square root of 21 is:
\( \sqrt{21} \approx 4.58257569495584 \)
- Continued Fraction Representation:
Square roots of non-perfect squares can also be represented as continued fractions, which provide an infinite series of fractions that get closer to the actual value. The continued fraction for \( \sqrt{21} \) is:
\( \sqrt{21} = 4 + \frac{1}{8 + \frac{1}{8 + \frac{1}{8 + \ldots}}} \)
- Prime Factorization Method:
Although prime factorization does not simplify the square root of 21, it helps in understanding its components:
\( 21 = 3 \times 7 \)
This indicates that the square root of 21 involves the square roots of 3 and 7, both of which are irrational numbers.
- Graphical Representation:
On a number line, the square root of 21 can be approximated between the integers 4 and 5. A more precise graphical method involves plotting the function \( y = \sqrt{x} \) and locating the point where \( x = 21 \).
- Properties of Square Roots:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- \( (\sqrt{a})^2 = a \)
Understanding the mathematical representation of the square root of 21 allows for a deeper comprehension of its properties and applications in various mathematical contexts.
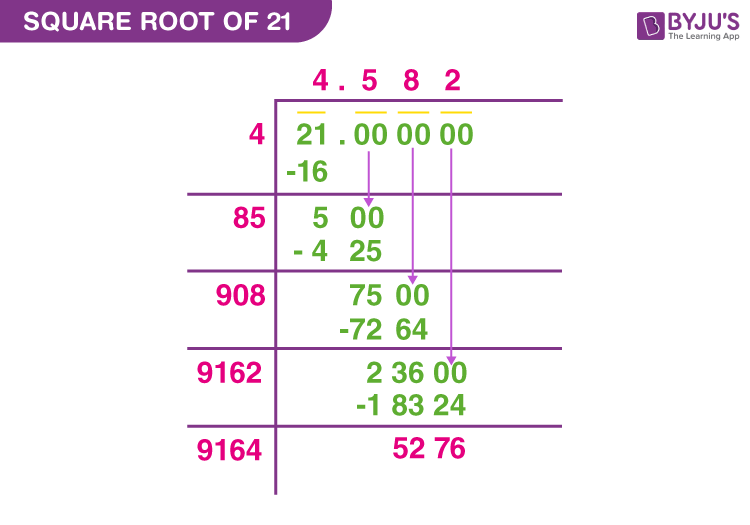
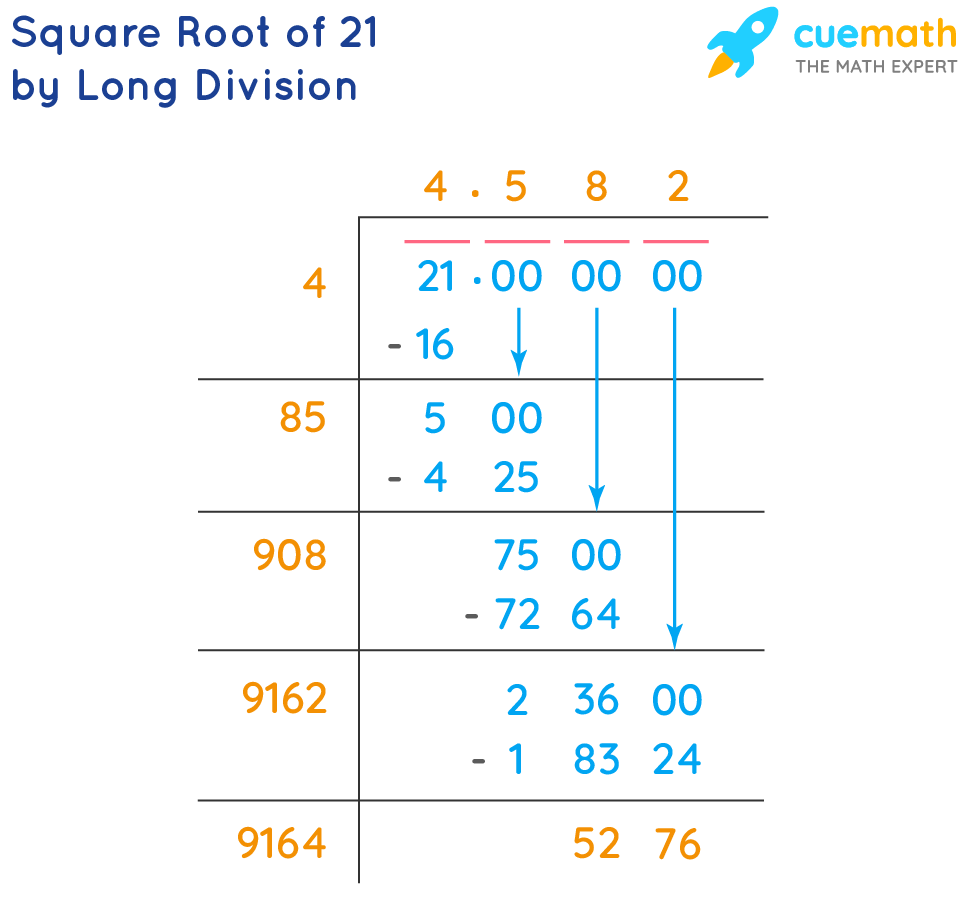
Calculation Methods
Calculating the square root of 21 involves several methods, each with varying degrees of complexity and accuracy. Below are some common methods for finding the square root of 21, explained step-by-step.
- Long Division Method:
The long division method is a manual process to find the square root of a number with high precision.
- Pair the digits of 21 from right to left. Since 21 has only two digits, we consider it as one pair: 21.
- Find the largest number whose square is less than or equal to 21. This number is 4 because \(4^2 = 16\).
- Subtract \(16\) from 21 to get 5. Bring down two zeros to get 500.
- Double the divisor (4) to get 8, and determine how many times 8 can fit into 50 (the first part of 500). The answer is 6 (because 86 x 6 = 516, which is slightly above 500).
- Repeat the process to obtain more decimal places.
This method approximates \( \sqrt{21} \approx 4.5825 \).
- Estimation and Refinement:
This method uses simple arithmetic and iterative steps to approximate the square root.
- Estimate a rough value. We know \(4^2 = 16\) and \(5^2 = 25\), so \( \sqrt{21} \) is between 4 and 5.
- Try a number in between, say 4.5: \(4.5^2 = 20.25\), which is close to 21.
- Refine the estimate by trying a number slightly higher, such as 4.6: \(4.6^2 = 21.16\), which is slightly more than 21.
- Continue refining until you get the desired precision. This can be automated using algorithms in calculators or computers.
- Using a Calculator:
The most straightforward method for most people is to use a scientific calculator:
- Enter the number 21.
- Press the square root button (usually denoted as \( \sqrt{} \) or "sqrt").
- The calculator displays the result, approximately \(4.58257569495584\).
- Newton's Method (Newton-Raphson Method):
This iterative method provides a highly accurate approximation by using calculus principles.
- Start with an initial guess \( x_0 \). For \( \sqrt{21} \), let's start with \( x_0 = 4.5 \).
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{21}{x_n} \right) \) to get closer approximations.
- Apply the formula:
- First iteration: \( x_1 = \frac{1}{2} \left( 4.5 + \frac{21}{4.5} \right) \approx 4.5833 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 4.5833 + \frac{21}{4.5833} \right) \approx 4.5826 \)
- Repeat until the desired precision is achieved. This method converges quickly to \( \sqrt{21} \).
Each method provides a different approach to finding the square root of 21, ranging from manual calculations to iterative algorithms. Understanding these methods enhances our comprehension of numerical approximations and their applications.
Decimal Approximation
The square root of 21 is an irrational number, meaning it cannot be expressed exactly as a simple fraction, and its decimal representation is non-terminating and non-repeating. Here, we discuss the decimal approximation of \( \sqrt{21} \) in detail, using different methods to achieve accurate results.
- Initial Estimation:
To begin with, we know that \( \sqrt{21} \) lies between the square roots of 16 and 25, since \( 16 < 21 < 25 \). Therefore, \( \sqrt{16} = 4 \) and \( \sqrt{25} = 5 \). This gives us an initial estimate that \( \sqrt{21} \) is between 4 and 5.
- Long Division Method:
Using the long division method, we can calculate the square root to several decimal places:
- Pair the digits of 21, treating it as 21.0000 for additional precision.
- Find the largest number whose square is less than or equal to 21, which is 4 (since \( 4^2 = 16 \)).
- Subtract 16 from 21 to get 5. Bring down two zeros to make it 500.
- Double the 4 to get 8. Determine how many times 8 fits into 50. The answer is 6 (since \( 86 \times 6 = 516 \)).
- Continue the process to get more decimal places. This gives an approximation \( \sqrt{21} \approx 4.5825 \).
- Using a Calculator:
Most scientific calculators can compute square roots directly. Enter 21 and press the square root button to get:
\( \sqrt{21} \approx 4.58257569495584 \)
- Newton's Method:
This iterative method provides a highly accurate approximation:
- Start with an initial guess, say \( x_0 = 4.5 \).
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{21}{x_n} \right) \).
- First iteration: \( x_1 = \frac{1}{2} \left( 4.5 + \frac{21}{4.5} \right) \approx 4.5833 \).
- Second iteration: \( x_2 = \frac{1}{2} \left( 4.5833 + \frac{21}{4.5833} \right) \approx 4.5826 \).
- Repeat until desired precision is achieved. The method converges quickly to \( \sqrt{21} \).
- Continued Fraction Representation:
Another method involves expressing \( \sqrt{21} \) as a continued fraction:
\( \sqrt{21} = 4 + \frac{1}{8 + \frac{1}{8 + \frac{1}{8 + \ldots}}} \)
This provides an infinite series of fractions that converge to the exact value.
Using these methods, we approximate \( \sqrt{21} \) to a high degree of accuracy, enhancing our understanding of irrational numbers and their properties.
Prime Factorization
The prime factorization of a number involves expressing the number as a product of its prime factors. However, 21 is not a perfect square, so we approach this by factorizing 21 into its prime factors and understanding how the square root relates to these factors.
First, let's determine the prime factors of 21:
- 21 can be divided by 3 (which is a prime number), giving us 21 ÷ 3 = 7.
- 7 is also a prime number.
So, the prime factorization of 21 is:
21 = 3 × 7
To find the square root of 21 using its prime factorization, we recognize that the square root of a product is the product of the square roots of the factors:
\(\sqrt{21} = \sqrt{3 \times 7} = \sqrt{3} \times \sqrt{7}\)
Since both \(\sqrt{3}\) and \(\sqrt{7}\) are irrational numbers, their product, \(\sqrt{21}\), is also an irrational number. The exact value of \(\sqrt{21}\) cannot be simplified further using prime factorization.
To better understand the value, we can look at the decimal approximation, which is approximately 4.582.
This method shows how prime factorization helps in breaking down the components of a number, even though it doesn't simplify the square root of 21 into a rational number.
Irrational Numbers
An irrational number is a number that cannot be expressed as a simple fraction, meaning its decimal representation is non-repeating and non-terminating. The square root of 21 is one such number.
Let's understand why the square root of 21 is considered an irrational number:
- By definition, an irrational number cannot be written as \(\frac{p}{q}\), where \(p\) and \(q\) are integers and \(q \neq 0\).
- The square root of 21, denoted as \(\sqrt{21}\), does not result in a finite or repeating decimal.
To delve deeper, let's examine the nature of the square root of 21:
\(\sqrt{21} \approx 4.58257569495584...\)
The decimal representation goes on forever without repeating, which is a hallmark of an irrational number.
We can also understand this through prime factorization:
- The prime factors of 21 are 3 and 7.
- \(\sqrt{21} = \sqrt{3 \times 7} = \sqrt{3} \times \sqrt{7}\).
- Both \(\sqrt{3}\) and \(\sqrt{7}\) are known to be irrational numbers.
- The product of two irrational numbers (in this case, \(\sqrt{3} \times \sqrt{7}\)) is also irrational.
Thus, the square root of 21 cannot be simplified to a rational number and remains irrational. This irrationality has several implications in mathematics and real-life applications:
- Mathematical Implications: The properties of irrational numbers are crucial in fields such as number theory and algebra. They help in understanding the distribution of numbers and the structure of the real number system.
- Real-Life Applications: Irrational numbers like \(\sqrt{21}\) are used in various calculations involving geometry, physics, and engineering, where precise measurements are necessary.
In summary, \(\sqrt{21}\) exemplifies the characteristics of an irrational number through its non-repeating, non-terminating decimal expansion and its prime factorization. This understanding enriches our comprehension of the broader category of irrational numbers in mathematics.
Properties of Square Root of 21
The square root of 21, denoted as \(\sqrt{21}\), possesses several interesting properties. These properties help us understand the nature and behavior of this irrational number in various mathematical contexts.
- Irrationality: The square root of 21 is an irrational number. This means it cannot be expressed as a fraction \(\frac{p}{q}\), where \(p\) and \(q\) are integers, and \(q \neq 0\). Its decimal expansion is non-terminating and non-repeating.
- Decimal Approximation: The approximate value of \(\sqrt{21}\) is 4.58257569495584. This approximation is useful for practical calculations where an exact value is not necessary.
- Prime Factorization Relationship: While 21 can be factorized into prime numbers as 3 and 7, \(\sqrt{21}\) can be expressed in terms of the square roots of these primes: \(\sqrt{21} = \sqrt{3 \times 7} = \sqrt{3} \times \sqrt{7}\). Both \(\sqrt{3}\) and \(\sqrt{7}\) are irrational, contributing to the irrationality of \(\sqrt{21}\).
- Algebraic Properties:
- Addition and Subtraction: \(\sqrt{21}\) can be used in addition and subtraction with other irrational or rational numbers. For example, \( \sqrt{21} + 2 \) or \( \sqrt{21} - \sqrt{3} \).
- Multiplication and Division: \(\sqrt{21}\) can be multiplied or divided by rational or irrational numbers. For instance, \( \sqrt{21} \times 2 = 2\sqrt{21} \) and \( \frac{\sqrt{21}}{\sqrt{7}} = \sqrt{3} \).
- Conjugate: The conjugate of \(\sqrt{21}\) is -\(\sqrt{21}\). This property is useful in rationalizing denominators when dealing with fractions involving \(\sqrt{21}\).
- Quadratic Equations: \(\sqrt{21}\) can be a solution to quadratic equations. For example, solving \(x^2 = 21\) yields \(x = \pm\sqrt{21}\).
- Geometric Interpretation: In a geometric context, \(\sqrt{21}\) represents the length of the hypotenuse of a right-angled triangle with legs of lengths \(\sqrt{3}\) and \(\sqrt{7}\), according to the Pythagorean theorem.
These properties highlight the significance of \(\sqrt{21}\) in various mathematical and real-world applications, demonstrating its utility beyond just being an irrational number.
Applications in Mathematics
The square root of 21, denoted as \(\sqrt{21}\), finds various applications in different fields of mathematics. Here are some notable applications:
- Algebra:
- Solving Quadratic Equations: The square root of 21 can appear as a solution in quadratic equations. For instance, the equation \(x^2 = 21\) has solutions \(x = \pm\sqrt{21}\).
- Radical Expressions: \(\sqrt{21}\) is used in simplifying and solving radical expressions. For example, \(\sqrt{84} = 2\sqrt{21}\).
- Geometry:
- Distance and Length: The square root of 21 can represent distances and lengths in geometric problems. For example, in the context of the distance formula, the distance between two points in a coordinate plane can be \(\sqrt{21}\).
- Right Triangles: \(\sqrt{21}\) can be the hypotenuse or leg of a right triangle. If one leg is \(\sqrt{3}\) and the other is \(\sqrt{7}\), the hypotenuse is \(\sqrt{3^2 + 7^2} = \sqrt{21}\).
- Trigonometry:
- Trigonometric Functions: The value of \(\sqrt{21}\) is used in defining certain trigonometric functions, especially when dealing with specific angles in right triangles.
- Calculus:
- Limits and Continuity: The square root function \(\sqrt{x}\) is often evaluated at specific points, including \(\sqrt{21}\), to study limits and continuity.
- Integrals and Derivatives: \(\sqrt{21}\) can appear in the process of integration and differentiation, especially when dealing with functions involving square roots.
- Number Theory:
- Irrational Numbers: \(\sqrt{21}\) serves as an example when studying properties and characteristics of irrational numbers in number theory.
- Mathematical Constants:
- Approximations: The value of \(\sqrt{21}\) (approximately 4.5826) is used in approximations and numerical methods, where exact values are not necessary, but close approximations are useful.
These applications demonstrate the versatility and importance of the square root of 21 in various branches of mathematics, highlighting its utility in theoretical and practical contexts.
Real-Life Applications
The square root of 21, denoted as \(\sqrt{21}\), is not just a theoretical concept in mathematics; it also has practical applications in various real-life contexts. Here are some detailed examples:
- Engineering and Construction:
- Structural Design: Engineers use the square root of 21 in calculations involving the design and analysis of structures, where precise measurements and proportions are crucial.
- Material Stress: Calculations involving load, stress, and material strength can include \(\sqrt{21}\) as part of the equations that determine safety and durability.
- Physics:
- Wave Mechanics: In wave mechanics, certain equations involving wave speed and frequency might include \(\sqrt{21}\) as part of the solution.
- Optics: Calculations involving the refractive index and light propagation through different media can use \(\sqrt{21}\) to determine precise values.
- Architecture:
- Design Proportions: Architects may use \(\sqrt{21}\) to achieve aesthetically pleasing proportions and balance in their designs.
- Computer Graphics:
- Rendering Calculations: In computer graphics, square roots are used in rendering calculations to determine distances, lighting, and shading effects. \(\sqrt{21}\) might be part of these complex calculations.
- Navigation and GPS:
- Distance Calculations: GPS systems use the square root function to calculate distances between points on the Earth’s surface. \(\sqrt{21}\) can appear in these algorithms when calculating specific routes.
- Environmental Science:
- Modeling and Simulations: Environmental models and simulations often involve equations with square roots to predict phenomena like pollutant dispersion and resource distribution. \(\sqrt{21}\) can be part of these critical calculations.
- Art and Design:
- Pattern Creation: Artists and designers sometimes use mathematical constants and square roots to create patterns and designs that have a natural and appealing balance. \(\sqrt{21}\) can be used in such creative processes.
These examples illustrate how \(\sqrt{21}\) is integrated into various fields, demonstrating its significance beyond pure mathematics and highlighting its utility in solving real-world problems.
Common Misconceptions
The square root of 21, denoted as \(\sqrt{21}\), is often misunderstood due to its irrational nature and its mathematical properties. Here are some common misconceptions, clarified in a detailed and positive manner:
- Misconception 1: \(\sqrt{21}\) is a Rational Number
One common misconception is that \(\sqrt{21}\) is a rational number. In reality, \(\sqrt{21}\) is an irrational number, meaning it cannot be expressed as a simple fraction \(\frac{p}{q}\), where \(p\) and \(q\) are integers and \(q \neq 0\). Its decimal representation is non-terminating and non-repeating.
- Misconception 2: \(\sqrt{21}\) can be Simplified to a Whole Number
Another misconception is that \(\sqrt{21}\) can be simplified to a whole number. This is not possible because 21 is not a perfect square. The value of \(\sqrt{21}\) is approximately 4.58257569495584, which is not a whole number.
- Misconception 3: Prime Factorization of 21 Affects its Irrationality
Some believe that since 21 can be expressed as a product of prime factors (3 and 7), the square root of 21 should be rational. However, the irrationality of \(\sqrt{21}\) is not affected by the prime factorization of 21. The square roots of 3 and 7 are both irrational, and their product, \(\sqrt{3} \times \sqrt{7}\), remains irrational.
- Misconception 4: \(\sqrt{21}\) is Not Useful in Practical Applications
There is a misconception that irrational numbers like \(\sqrt{21}\) are not useful in practical applications. In fact, \(\sqrt{21}\) is used in various fields such as engineering, physics, computer graphics, and environmental science, where precise measurements and calculations are required.
- Misconception 5: Irrational Numbers are Rarely Encountered
Many people think that irrational numbers are rare and seldom encountered. On the contrary, irrational numbers are quite common in mathematics and appear frequently in various contexts, such as geometric measurements, trigonometric functions, and natural constants.
Understanding these misconceptions helps in gaining a clearer and more accurate perspective of the properties and applications of \(\sqrt{21}\), showcasing its significance in both theoretical and practical contexts.
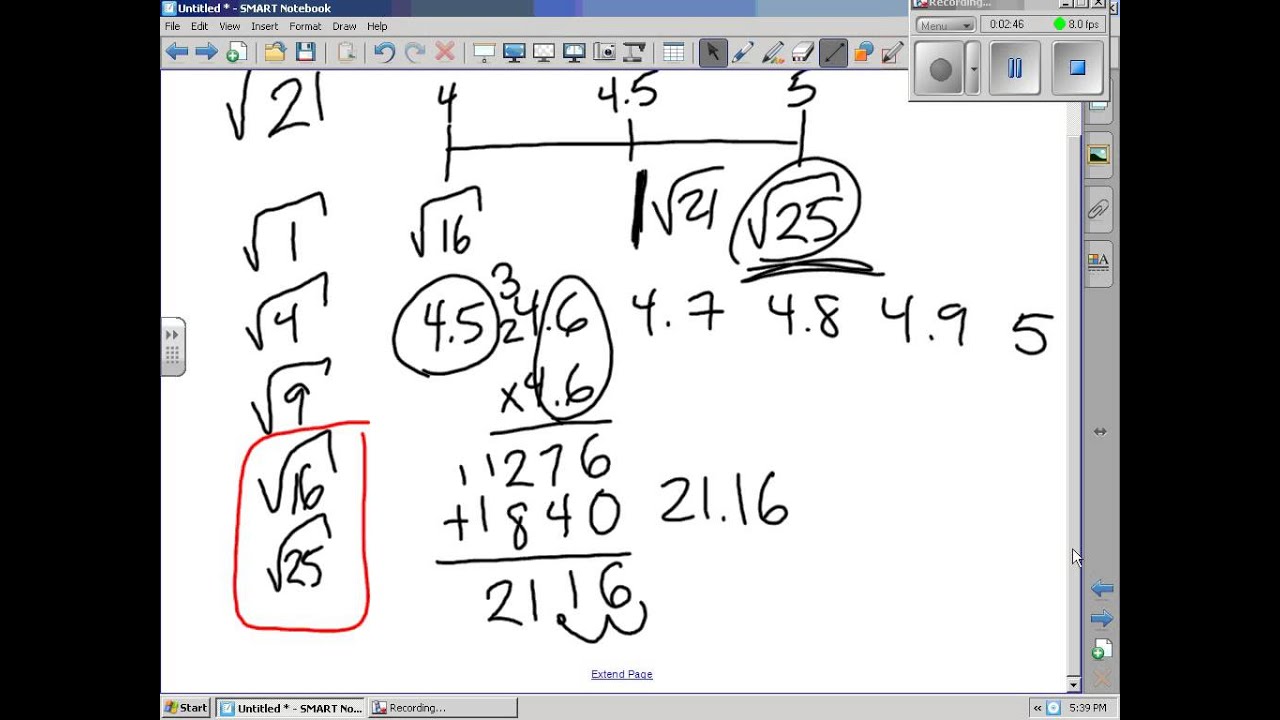
Visual Representation
The square root of 21, denoted as \(\sqrt{21}\), can be visually represented in various ways to help understand its value and properties. Here are some detailed visual representations:
- Number Line:
Placing \(\sqrt{21}\) on a number line helps visualize its approximate value between whole numbers. It is located between 4 and 5, closer to 4.6.

- Geometric Representation:
\(\sqrt{21}\) can be visualized as the length of the hypotenuse in a right-angled triangle. Consider a triangle with legs of lengths \(\sqrt{3}\) and \(\sqrt{7}\). According to the Pythagorean theorem:
\[ \text{Hypotenuse} = \sqrt{(\sqrt{3})^2 + (\sqrt{7})^2} = \sqrt{3 + 7} = \sqrt{21} \]

- Square Root Spiral (Theodorus' Spiral):
The square root spiral, or Theodorus' spiral, is another way to visualize \(\sqrt{21}\). This spiral is constructed using right-angled triangles where the hypotenuse of each successive triangle is the square root of the next integer. The hypotenuse representing \(\sqrt{21}\) can be highlighted within the spiral.

- Graphical Representation:
On a graph, the function \(y = \sqrt{x}\) can be plotted to show the value of \(\sqrt{21}\). The point where \(x = 21\) on the curve gives the corresponding \(y\) value, which is approximately 4.5826.

These visual representations help in understanding the magnitude and properties of \(\sqrt{21}\) in a more intuitive and comprehensive manner.
Historical Context
The concept of the square root, including that of 21, has a rich historical context, reflecting the evolution of mathematical understanding over centuries. Here is a detailed look at the historical development related to square roots:
- Ancient Civilizations:
Ancient Egyptians and Babylonians were among the first to use square roots in their calculations. They used methods to approximate square roots for practical purposes such as land measurement and construction.
- Greek Mathematics:
Greek mathematicians like Pythagoras and Euclid made significant contributions to the theory of square roots. The Pythagorean theorem, for example, relates the square roots to the sides of a right triangle, a fundamental principle in geometry.
- Indian Mathematicians:
Indian mathematicians such as Aryabhata and Brahmagupta further developed methods for finding square roots. Aryabhata’s work in the 5th century included algorithms for calculating square roots, which influenced later mathematical practices.
- Islamic Golden Age:
During the Islamic Golden Age, scholars like Al-Khwarizmi expanded on the work of their Greek and Indian predecessors. Al-Khwarizmi’s book "The Compendious Book on Calculation by Completion and Balancing" included detailed methods for solving quadratic equations, which inherently involve square roots.
- European Renaissance:
During the Renaissance, European mathematicians began to adopt and adapt the knowledge from ancient and medieval sources. Mathematicians like Fibonacci introduced Arabic numerals and algebraic concepts, including the use of square roots, to Europe. Fibonacci's "Liber Abaci" was instrumental in spreading this knowledge.
- Modern Mathematics:
In the modern era, the understanding of square roots has been formalized within the broader framework of real and complex numbers. The development of calculus and the rigorous definition of limits and continuity by mathematicians like Newton and Leibniz further advanced the comprehension of square roots, including irrational numbers like \(\sqrt{21}\).
The historical journey of square roots from ancient practical calculations to their formal mathematical treatment illustrates the enduring importance and fascination of this concept in the field of mathematics.
Advanced Topics
The square root of 21, denoted as \(\sqrt{21}\), can be explored through various advanced mathematical topics. These topics delve deeper into the properties and applications of square roots in complex mathematical contexts:
- Complex Numbers:
While \(\sqrt{21}\) is a real number, it can be extended into the complex plane. For any real number \(x\), the square root can be expressed as a complex number when considering negative values:
\[ \sqrt{-x} = i\sqrt{x} \]
Where \(i\) is the imaginary unit. For example, the square root of \(-21\) is \(i\sqrt{21}\).
- Continued Fractions:
The square root of 21 can be expressed as a continued fraction, which is a way of representing numbers through an infinite sequence of fractions. The continued fraction representation of \(\sqrt{21}\) is:
\[ \sqrt{21} = 4 + \frac{1}{\overline{8 + \frac{1}{8 + \frac{1}{8 + \cdots}}}} \]
This periodic continued fraction highlights the unique properties of irrational numbers.
- Numerical Methods:
Advanced numerical methods can be used to approximate \(\sqrt{21}\) with high precision. Techniques such as the Newton-Raphson method iteratively improve estimates of the square root:
For a function \(f(x) = x^2 - 21\), the Newton-Raphson iteration is:
\[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} = x_n - \frac{x_n^2 - 21}{2x_n} \]
Starting with an initial guess \(x_0\), this method converges to \(\sqrt{21}\).
- Eigenvalues and Eigenvectors:
In linear algebra, the square root of 21 can appear as an eigenvalue in specific matrices. For example, consider a 2x2 matrix whose determinant and trace lead to eigenvalues involving \(\sqrt{21}\):
\[ A = \begin{pmatrix} 10 & 1 \\ 1 & 12 \end{pmatrix} \]
The characteristic equation is:
\[ \text{det}(A - \lambda I) = \lambda^2 - 22\lambda + 119 = 0 \]
Solving this yields eigenvalues that can include \(\sqrt{21}\) as part of their calculation.
- Field Extensions:
In abstract algebra, the field extension \(\mathbb{Q}(\sqrt{21})\) involves creating a field that includes all rational numbers and \(\sqrt{21}\). This field has unique properties and applications in solving polynomial equations.
These advanced topics demonstrate the deeper mathematical significance and applications of \(\sqrt{21}\), highlighting its role in various complex mathematical theories and methods.
Conclusion
Understanding the square root of 21 involves recognizing its unique properties and applications. The square root of 21, approximately 4.582, is an irrational number, meaning it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion. This mathematical concept has been explored through various methods such as the prime factorization, estimation, long division, and using calculators.
Although 21 is not a perfect square, the methods of finding its square root highlight important mathematical techniques and concepts. The square root of 21 demonstrates the use of both historical and modern calculation methods, reflecting the evolution of mathematical understanding.
In real-life applications, the square root of 21 can be utilized in fields such as geometry, engineering, and physics, where precise measurements and calculations are essential. By appreciating the properties and calculations of the square root of 21, one gains a deeper insight into the broader realm of mathematics and its practical significance.
Overall, the exploration of the square root of 21 not only enriches one's mathematical knowledge but also underscores the importance of continued learning and application of mathematical principles in various aspects of life.
Khám phá cách tính căn bậc hai của 21 và ứng dụng trong cuộc sống với video hướng dẫn chi tiết bằng tiếng Việt.
Căn Bậc Hai Của 21: Hướng Dẫn Toàn Diện
READ MORE:
Khám phá căn bậc hai của 21 và các phương pháp tính toán trong video hướng dẫn chi tiết bằng tiếng Việt.
Căn Bậc Hai 21