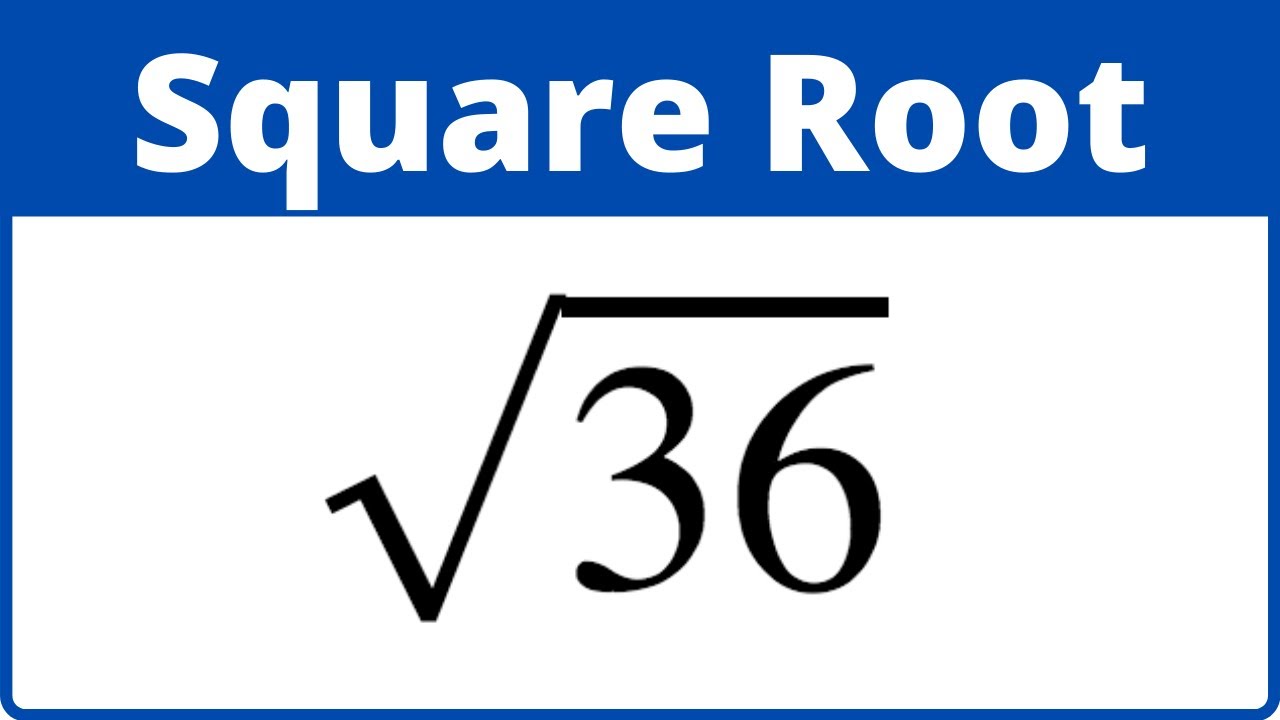
Topic what is the positive square root of 36: The positive square root of 36 is a fundamental concept in mathematics. In this article, we'll explore what it means, how to calculate it, and its significance in various applications. Understanding the positive square root of 36 can enhance your math skills and provide insights into more complex mathematical topics.
Table of Content
- What is the Positive Square Root of 36?
- Introduction to Square Roots
- Understanding the Concept of Positive Square Roots
- Mathematical Definition of Square Roots
- Calculating the Square Root of 36
- Why 6 is the Positive Square Root of 36
- Properties of Square Roots
- Applications of Square Roots in Real Life
- Common Mistakes in Calculating Square Roots
- Advanced Topics: Complex Square Roots
- Frequently Asked Questions about Square Roots
- Conclusion: The Importance of Understanding Square Roots
- YOUTUBE: Khám phá lý do tại sao căn bậc hai của 36 chỉ là số 6 dương trong video này.
What is the Positive Square Root of 36?
The positive square root of a number is the non-negative value that, when multiplied by itself, gives the original number. In this case, we are looking for the positive square root of 36.
Calculation
To find the positive square root of 36, we need to determine the number that, when squared (multiplied by itself), equals 36.
Mathematically, this is represented as:
\[ \sqrt{36} = x \]
Where \( x \) is the positive square root.
We know that:
\[ x^2 = 36 \]
Solving for \( x \), we get:
\[ x = \sqrt{36} \]
The value of \( x \) that satisfies this equation is:
\[ x = 6 \]
Conclusion
Therefore, the positive square root of 36 is 6.
| Number | Positive Square Root |
| 36 | 6 |
- The positive square root is always non-negative.
- For any positive number \( n \), \( \sqrt{n} \) is the positive square root of \( n \).
- In this case, \( \sqrt{36} = 6 \).

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics that involve finding a number which, when multiplied by itself, gives the original number. This process is denoted by the radical symbol (√). For example, the square root of 36 is a number that, when squared, equals 36.
In mathematical terms, the square root of a number x is a number y such that:
\[ y^2 = x \]
For positive numbers, there are always two square roots: one positive and one negative. However, when we refer to the positive square root, we are interested in the non-negative solution.
Let's break down the concept further:
- Radical Symbol (√): The symbol used to denote the square root. For instance, √36 represents the square root of 36.
- Perfect Squares: Numbers that have integer square roots. Examples include 1, 4, 9, 16, 25, and 36.
- Non-Perfect Squares: Numbers that do not have integer square roots. Their square roots are irrational numbers, such as √2 or √5.
Calculating the square root can be straightforward for perfect squares, but it often involves approximations or the use of a calculator for non-perfect squares.
Here's a simple example:
| Number | Positive Square Root |
| 36 | 6 |
Understanding square roots is essential for solving various mathematical problems and is widely used in different fields such as physics, engineering, and finance.
Understanding the Concept of Positive Square Roots
The concept of positive square roots is fundamental in mathematics. A square root of a number x is a number y such that when y is multiplied by itself, it equals x. Mathematically, this is expressed as:
\[ y^2 = x \]
For any given positive number, there are two square roots: one positive and one negative. The positive square root is the non-negative value. For example, the positive square root of 36 is 6 because:
\[ 6 \times 6 = 36 \]
In general, the square root function is denoted by the radical symbol (√). Thus, the positive square root of 36 is represented as:
\[ \sqrt{36} = 6 \]
To further understand the concept, consider the following properties and examples:
- Non-Negative Output: The positive square root of any positive number is always non-negative.
- Unique Positive Value: For every positive number x, there is a unique positive square root.
- Perfect Squares: Numbers like 1, 4, 9, 16, 25, and 36 are perfect squares because their square roots are integers.
- Non-Perfect Squares: Numbers like 2, 3, 5, and 7 are not perfect squares, and their square roots are irrational numbers.
Here is a table of some common perfect squares and their positive square roots:
| Number | Positive Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
By understanding the concept of positive square roots, you can solve various mathematical problems and gain a deeper insight into the properties of numbers.
Mathematical Definition of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. This concept is fundamental in mathematics and is denoted by the radical symbol (√). If x is a non-negative number, the square root of x is written as \( \sqrt{x} \).
Mathematically, the square root of a number x is defined as:
\[ \sqrt{x} = y \quad \text{such that} \quad y^2 = x \]
Where:
- x is the original number.
- \( y \) is the square root of x.
For example, the positive square root of 36 can be found as follows:
\[ \sqrt{36} = 6 \quad \text{since} \quad 6^2 = 36 \]
Square roots can be categorized into perfect squares and non-perfect squares:
- Perfect Squares: Numbers whose square roots are integers. Examples include 1, 4, 9, 16, 25, and 36.
- Non-Perfect Squares: Numbers whose square roots are not integers. Examples include 2, 3, 5, and 7.
To understand this further, let's look at some properties of square roots:
- Non-Negative Output: The principal (positive) square root of a non-negative number is always non-negative.
- Uniqueness: Every non-negative number x has a unique non-negative square root.
- Product Property: The square root of a product is the product of the square roots: \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \].
- Quotient Property: The square root of a quotient is the quotient of the square roots: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] for \( b \neq 0 \).
Here's a table illustrating some perfect squares and their positive square roots:
| Number | Positive Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
Understanding the mathematical definition of square roots provides a foundation for more advanced mathematical concepts and problem-solving techniques.
Calculating the Square Root of 36
Calculating the square root of 36 involves finding a number that, when multiplied by itself, equals 36. This process can be understood through a series of simple steps.
- Identify the number: We start with the number 36.
- Set up the equation: The goal is to find a number x such that:
\[ x^2 = 36 \]
- Consider perfect squares: Since 36 is a perfect square, its square root will be an integer. Common perfect squares and their roots include:
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- \( 5^2 = 25 \)
- \( 6^2 = 36 \)
- Determine the positive root: From the list above, we see that:
\[ 6 \times 6 = 36 \]
Therefore, the positive square root of 36 is 6.
- Verification: To verify, we can square the result:
\[ 6^2 = 36 \]
This confirms that 6 is indeed the positive square root of 36.
Understanding the calculation of square roots is essential for various mathematical applications. Here is a table summarizing the process for some common perfect squares:
| Number | Positive Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
By following these steps, one can easily calculate the square root of any perfect square, ensuring a clear and accurate understanding of the process.

Why 6 is the Positive Square Root of 36
The number 6 is the positive square root of 36 because when 6 is multiplied by itself, the product is 36. This relationship is fundamental to understanding square roots in mathematics. Let’s break down the reasons step by step:
- Definition of Square Root: The square root of a number x is a number y such that:
\[ y^2 = x \]
In this case, we are looking for a number y such that:
\[ y^2 = 36 \]
- Identifying Perfect Squares: A perfect square is an integer that is the square of another integer. Since 36 is a perfect square, its square root must also be an integer. The common perfect squares and their roots include:
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- \( 5^2 = 25 \)
- \( 6^2 = 36 \)
- Calculation: From the list above, it is clear that:
\[ 6 \times 6 = 36 \]
This calculation confirms that 6 is the positive square root of 36.
- Properties of Positive Square Roots: The positive square root is the non-negative root. For any positive number x, the positive square root is denoted by \( \sqrt{x} \):
\[ \sqrt{36} = 6 \]
This notation specifies the positive root of the number.
- Verification: To ensure the accuracy, we can verify by squaring the result:
\[ 6^2 = 36 \]
This confirms that the calculation is correct and that 6 is indeed the positive square root of 36.
Here is a table summarizing the verification of perfect squares and their positive square roots:
| Number | Positive Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
Understanding why 6 is the positive square root of 36 helps in grasping the broader concept of square roots and their applications in mathematics.
Properties of Square Roots
Square roots have several important properties that are fundamental in mathematics. Understanding these properties can help in various mathematical operations and problem-solving scenarios.
- Non-negativity: The square root of a non-negative number is also non-negative. This is because squaring a non-negative number always yields a non-negative result. For example, \( \sqrt{36} = 6 \) and \( \sqrt{0} = 0 \).
- Unique Positive Root: Every positive number has exactly one positive square root. For instance, the positive square root of 36 is 6, denoted as \( \sqrt{36} = 6 \).
- Product Property: The square root of a product is the product of the square roots of the factors. Mathematically, \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \). For example, \( \sqrt{36 \cdot 4} = \sqrt{36} \cdot \sqrt{4} = 6 \cdot 2 = 12 \).
- Quotient Property: The square root of a quotient is the quotient of the square roots of the numerator and the denominator. Expressed as \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{36}{4}} = \frac{\sqrt{36}}{\sqrt{4}} = \frac{6}{2} = 3 \).
- Exponentiation: The square root of a number can be represented as an exponent. Specifically, \( \sqrt{a} = a^{\frac{1}{2}} \). For example, \( \sqrt{36} = 36^{\frac{1}{2}} = 6 \).
- Square of a Square Root: The square of the square root of a number returns the original number. That is, \( (\sqrt{a})^2 = a \). For instance, \( (\sqrt{36})^2 = 6^2 = 36 \).
- Additivity and Subtractivity: Unlike multiplication and division, square roots do not distribute over addition or subtraction. For example, \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \) and \( \sqrt{a - b} \neq \sqrt{a} - \sqrt{b} \).
These properties are essential for simplifying expressions involving square roots and solving equations. They also have practical applications in various fields, including engineering, physics, and finance.
Applications of Square Roots in Real Life
Square roots play a crucial role in various real-life applications across different fields. Here are some key areas where square roots are applied:
- Engineering and Architecture: Square roots are used in engineering and architecture for calculations involving areas, volumes, and other measurements. For instance, determining the diagonal of a square requires the square root. If each side of a square is 6 units, the diagonal is \( \sqrt{6^2 + 6^2} = \sqrt{72} = 6\sqrt{2} \).
- Physics: In physics, square roots are used to calculate quantities like the root mean square velocity of gas molecules in thermodynamics, and in formulas like \( v = \sqrt{2gh} \) for the velocity of an object under free fall from a height \( h \) with gravitational acceleration \( g \).
- Finance: Square roots are used in finance to compute the volatility of stock prices. The standard deviation, a measure of volatility, is calculated using the square root of the variance. For example, if the variance of stock returns is 36, the standard deviation is \( \sqrt{36} = 6 \).
- Medicine: In medicine, the Body Mass Index (BMI) is often calculated using square roots. The formula is \( BMI = \frac{weight}{height^2} \), where height is in meters. For instance, if a person weighs 72 kg and is 1.8 meters tall, their BMI is \( \frac{72}{1.8^2} = \frac{72}{3.24} \approx 22.22 \).
- Astronomy: Square roots are used to calculate distances in astronomy. The distance modulus formula \( m - M = 5 \log_{10}(d) - 5 \) involves the square root when solving for the distance \( d \).
- Computer Science: Algorithms in computer science often use square roots, such as those for optimizing search algorithms and in graphics for calculating distances between points in two-dimensional or three-dimensional space.
- Construction: In construction, the Pythagorean theorem involves square roots to determine the length of the hypotenuse of a right triangle. For a right triangle with legs of 3 and 4 units, the hypotenuse is \( \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) units.
These applications demonstrate the versatility and importance of understanding square roots in both everyday tasks and complex scientific computations.
Common Mistakes in Calculating Square Roots
Calculating square roots can sometimes lead to errors, especially if certain principles and rules are not properly followed. Here are some common mistakes to watch out for and how to avoid them:
- Ignoring Negative Numbers: A common mistake is forgetting that negative numbers do not have real square roots. For example, \( \sqrt{-36} \) is not a real number; instead, it is an imaginary number, denoted as \( 6i \) where \( i \) is the imaginary unit.
- Misapplying the Product Property: Some people incorrectly assume that the square root of a sum is the sum of the square roots. For instance, \( \sqrt{36 + 64} \neq \sqrt{36} + \sqrt{64} \). Correctly, \( \sqrt{100} = 10 \), but \( \sqrt{36} + \sqrt{64} = 6 + 8 = 14 \).
- Forgetting to Simplify: When dealing with non-perfect squares, it's easy to forget to simplify the expression. For example, \( \sqrt{72} \) should be simplified to \( \sqrt{36 \times 2} = 6\sqrt{2} \).
- Incorrectly Using the Quotient Property: The quotient property states \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). Mistakes occur when this is not applied correctly. For example, \( \sqrt{\frac{36}{9}} = \frac{\sqrt{36}}{\sqrt{9}} = \frac{6}{3} = 2 \), not \( \sqrt{4} = 2 \).
- Confusing Square and Square Root: Sometimes, students confuse squaring a number with finding its square root. For example, \( 36^2 = 1296 \) is not the same as \( \sqrt{36} = 6 \).
- Overlooking Both Positive and Negative Roots: While the principal (positive) square root is often the focus, forgetting that every positive number has both a positive and a negative square root can be a mistake. For example, \( \sqrt{36} = \pm 6 \).
- Improperly Handling Complex Numbers: When dealing with negative under the square root, it's crucial to understand complex numbers. For instance, \( \sqrt{-36} = 6i \), where \( i \) is the imaginary unit.
By being aware of these common mistakes and understanding the correct methods for calculating square roots, you can avoid errors and solve square root problems more effectively.

Advanced Topics: Complex Square Roots
Square roots are not limited to real numbers; they can also be extended to complex numbers. Understanding complex square roots involves delving into the realm of imaginary and complex numbers, which are essential in advanced mathematics and engineering.
Complex numbers are numbers of the form \( a + bi \), where \( i \) is the imaginary unit, satisfying \( i^2 = -1 \). The square root of a negative number involves the imaginary unit.
Finding the Square Root of a Complex Number
To find the square root of a complex number, we use the polar form of the complex number. A complex number \( z = a + bi \) can be represented in polar form as \( z = r(\cos \theta + i \sin \theta) \), where \( r \) is the magnitude and \( \theta \) is the argument.
For example, consider \( z = -36 \). To find its square root:
- Convert \( z \) to polar form:
- \( r = |z| = \sqrt{36^2} = 36 \)
- \( \theta = \pi \) (since \( z \) lies on the negative real axis)
- Thus, \( z = 36(\cos \pi + i \sin \pi) \)
- Apply the square root to the polar form:
- \( \sqrt{z} = \sqrt{36} \left( \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \right) \)
- \( \sqrt{z} = 6 \left( 0 + i \cdot 1 \right) = 6i \)
General Formula for Complex Square Roots
The general formula to find the square roots of a complex number \( z = a + bi \) is given by:
- Let \( r = \sqrt{a^2 + b^2} \) (the magnitude)
- Let \( \theta = \tan^{-1} \left( \frac{b}{a} \right) \) (the argument)
- The square roots are:
- \( \sqrt{z} = \sqrt{r} \left( \cos \frac{\theta}{2} + i \sin \frac{\theta}{2} \right) \)
- and the second root is \( \sqrt{r} \left( \cos \frac{\theta + 2\pi}{2} + i \sin \frac{\theta + 2\pi}{2} \right) \)
Example: Square Root of a Complex Number
Find the square roots of \( z = 5 + 12i \):
- Calculate the magnitude: \( r = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \)
- Calculate the argument: \( \theta = \tan^{-1} \left( \frac{12}{5} \right) \)
- Find the square roots:
- \( \sqrt{z} = \sqrt{13} \left( \cos \frac{\theta}{2} + i \sin \frac{\theta}{2} \right) \)
- and the second root is \( \sqrt{13} \left( \cos \frac{\theta + 2\pi}{2} + i \sin \frac{\theta + 2\pi}{2} \right) \)
These steps illustrate how complex square roots are calculated and highlight the significance of understanding the polar form and the properties of complex numbers.
Frequently Asked Questions about Square Roots
Square roots can sometimes be confusing, so here are answers to some common questions to help clarify their properties and applications:
What is the positive square root of 36?
The positive square root of 36 is 6. This is because \( 6 \times 6 = 36 \).
Why do square roots have two values?
Square roots have two values, a positive and a negative, because both \( x \) and \( -x \) will satisfy the equation \( x^2 = a \). For example, \( \sqrt{36} = 6 \) and \( -\sqrt{36} = -6 \).
How do you find the square root of a number?
The square root of a number can be found using various methods:
- Prime Factorization: Factor the number into prime factors and pair them. For example, \( 36 = 2^2 \times 3^2 \), so \( \sqrt{36} = \sqrt{(2 \times 3)^2} = 6 \).
- Estimation: Find the nearest perfect squares and estimate between them.
- Calculator: Use a calculator to find the precise square root.
What is the difference between a perfect square and a non-perfect square?
A perfect square is an integer that is the square of another integer. For example, 36 is a perfect square because it is \( 6^2 \). A non-perfect square is a number that is not the square of an integer, such as 20.
Can square roots be negative?
While the principal square root is positive, square roots can be negative. For any positive number \( a \), both \( \sqrt{a} \) and \( -\sqrt{a} \) are valid square roots. However, when we refer to "the square root," we usually mean the positive square root.
What are imaginary square roots?
Imaginary square roots occur when taking the square root of a negative number. For example, \( \sqrt{-36} = 6i \), where \( i \) is the imaginary unit, defined as \( i^2 = -1 \).
How are square roots used in real life?
Square roots are used in various real-life applications, including:
- Geometry: Calculating distances and lengths.
- Physics: Describing physical properties such as velocity and energy.
- Finance: Computing interest rates and standard deviation in statistics.
- Engineering: Designing and analyzing systems and structures.
What is the relationship between squaring and square rooting?
Squaring a number and taking the square root are inverse operations. If \( x \) is a number, then \( (\sqrt{x})^2 = x \) and \( \sqrt{x^2} = |x| \).
Understanding these frequently asked questions can help in comprehending the concept of square roots and their applications more thoroughly.
Conclusion: The Importance of Understanding Square Roots
Understanding square roots is fundamental in mathematics and essential for a wide range of applications in various fields. Here are some key reasons why comprehending square roots is important:
- Mathematical Foundation: Square roots are a basic mathematical concept that form the foundation for more advanced topics such as algebra, calculus, and complex numbers. Mastery of square roots helps in understanding these higher-level concepts.
- Problem Solving: Square roots are often involved in solving equations and inequalities. For example, solving a quadratic equation like \( x^2 = 36 \) requires finding the square root of 36, which is 6 and -6.
- Geometric Applications: Square roots are used to calculate distances and lengths in geometry. For instance, the Pythagorean theorem, which determines the length of the hypotenuse of a right triangle, relies on square roots.
- Scientific Computations: In physics, engineering, and other sciences, square roots are used to describe various physical phenomena. For example, the formula for the period of a pendulum, \( T = 2\pi\sqrt{\frac{L}{g}} \), involves a square root.
- Statistical Analysis: In statistics, the standard deviation, a measure of data dispersion, is calculated using square roots. Understanding this helps in analyzing and interpreting data effectively.
- Financial Calculations: Square roots are used in finance to compute interest rates, volatility, and risk. For example, the formula for calculating compound interest involves square roots when determining the rate of return.
- Real-Life Applications: Square roots are encountered in everyday life, from determining dimensions in construction projects to calculating speeds and areas. For example, to find the side length of a square with an area of 36 square units, one needs to compute the square root of 36, which is 6.
By understanding square roots, individuals can enhance their mathematical skills and apply this knowledge to solve practical problems in various domains. The ability to work with square roots not only improves quantitative reasoning but also fosters critical thinking and analytical skills.
In conclusion, the importance of understanding square roots extends beyond academic pursuits, playing a crucial role in numerous aspects of daily life and professional fields. Mastery of this concept enables better problem-solving abilities and a deeper comprehension of the world around us.
Khám phá lý do tại sao căn bậc hai của 36 chỉ là số 6 dương trong video này.
Tại sao sqrt(36) chỉ là 6 dương
READ MORE:
Tìm hiểu về căn bậc hai của 36 và lý do tại sao nó chỉ là số 6 dương trong video này.
Căn Bậc Hai của 36