Topic how to find square root of 225: Discover the easiest and most effective ways to find the square root of 225. In this comprehensive guide, we explore various methods including prime factorization, exponents, and long division, ensuring you understand each step clearly. Whether you're a student or just curious, this article makes learning fun and straightforward.
Table of Content
- How to Find the Square Root of 225
- Introduction to Square Roots
- Basic Concepts of Square Roots
- Prime Factorization Method
- Exponent Method
- Long Division Method
- Using a Calculator
- Understanding Perfect Squares
- Visual Representation of Square Roots
- Historical Methods for Finding Square Roots
- Practical Applications of Square Roots
- Advanced Techniques for Finding Square Roots
- Common Mistakes and How to Avoid Them
- Frequently Asked Questions (FAQs)
- Conclusion
- YOUTUBE:
How to Find the Square Root of 225
Finding the square root of 225 can be done using various methods. Below, we explain some common approaches:
1. Using Prime Factorization
The prime factorization method involves expressing 225 as a product of its prime factors:
- Start by dividing 225 by the smallest prime number, which is 5:
- Next, divide 45 by 5 again:
- Finally, divide 9 by 3:
- Group the prime factors into pairs:
- Take one number from each pair:
225 ÷ 5 = 45
45 ÷ 5 = 9
9 ÷ 3 = 3
So, 225 can be expressed as: \(225 = 5 \times 5 \times 3 \times 3\).
\(225 = (5 \times 3) \times (5 \times 3) = 15 \times 15\)
\(\sqrt{225} = 15\)
2. Using the Exponent Method
Another way to find the square root is by using exponents:
- Express 225 as a power of 2:
- Apply the square root:
\(225 = 15^2\)
\(\sqrt{225} = \sqrt{15^2} = 15\)
3. Using Long Division Method
The long division method is a manual technique for finding square roots. Here’s how you can apply it:
- Pair the digits of 225 from right to left (i.e., 2 25).
- Find the largest number whose square is less than or equal to the first pair (2). This number is 1:
- Subtract and bring down the next pair:
- Double the quotient (1) and find a digit (x) such that \(2x \times x\) is less than or equal to 125. The number is 5:
- Thus, the quotient is 15 and the square root of 225 is 15:
\(1 \times 1 = 1\)
\(2 - 1 = 1\); bring down 25 to make 125.
\(25 \times 5 = 125\)
\(\sqrt{225} = 15\)
4. Using a Calculator
The simplest method is to use a calculator:
- Enter 225.
- Press the square root button (√).
- The result will be 15.
Therefore, the square root of 225 is \( \sqrt{225} = 15 \).

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, helping to simplify expressions and solve equations. The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 225 is the number that satisfies the equation \( x^2 = 225 \). Understanding square roots is crucial for various mathematical applications, including algebra, geometry, and calculus.
Here are some essential points about square roots:
- The square root of a number \( n \) is denoted as \( \sqrt{n} \).
- Square roots can be both positive and negative because \( (-x)^2 = x^2 \).
- Perfect squares are numbers whose square roots are integers (e.g., 225 is a perfect square because \( \sqrt{225} = 15 \)).
To find the square root of 225, several methods can be used:
- Prime Factorization: Breaking down the number into its prime factors.
- Exponent Method: Using the properties of exponents to simplify the expression.
- Long Division: A manual technique for finding the square root by division.
- Calculator: The quickest method, using a digital calculator to find the square root.
Each of these methods offers a different approach to understanding and calculating square roots, providing multiple pathways to mastering this important mathematical concept.
Basic Concepts of Square Roots
Square roots are a fundamental concept in mathematics. They are the inverse operation of squaring a number. The square root of a number \( n \) is a value \( x \) such that \( x^2 = n \). This means that when \( x \) is multiplied by itself, the result is \( n \).
Key concepts related to square roots include:
- Notation: The square root of \( n \) is denoted as \( \sqrt{n} \).
- Positive and Negative Roots: Every positive number has two square roots, one positive and one negative. For example, both 15 and -15 are square roots of 225 because \( 15^2 = 225 \) and \( (-15)^2 = 225 \).
- Perfect Squares: A number is a perfect square if its square root is an integer. For example, 225 is a perfect square because \( \sqrt{225} = 15 \).
To find the square root of a number like 225, various methods can be used:
- Prime Factorization: Breaking down 225 into its prime factors.
- 225 can be factored into \( 5 \times 5 \times 3 \times 3 \).
- Grouping the factors into pairs: \( (5 \times 3) \times (5 \times 3) \).
- The square root of 225 is 15 because \( 15 \times 15 = 225 \).
- Exponent Method: Using the properties of exponents.
- Express 225 as \( 15^2 \).
- Apply the square root: \( \sqrt{15^2} = 15 \).
- Long Division Method: A step-by-step manual calculation.
- Pair the digits from right to left: 2 and 25.
- Find the largest number whose square is less than or equal to the first pair (2). This number is 1.
- Subtract and bring down the next pair to make 125.
- Double the quotient (1) and find a digit (x) such that \( 2x \times x \) is less than or equal to 125. The number is 5.
- The quotient is 15, and \( 15 \times 15 = 225 \).
- Calculator: Using a digital calculator for quick results.
- Enter 225 and press the square root button (√).
- The result is 15.
Understanding these basic concepts and methods allows for a deeper comprehension of how to calculate and utilize square roots in various mathematical contexts.
Prime Factorization Method
The prime factorization method involves breaking down a number into its prime factors. This method is straightforward and helps in understanding the structure of numbers. Here’s a step-by-step guide to find the square root of 225 using prime factorization:
- Identify Prime Factors:
- Start by dividing 225 by the smallest prime number, which is 5:
- \( 225 \div 5 = 45 \)
- Next, divide 45 by 5 again:
- \( 45 \div 5 = 9 \)
- Finally, divide 9 by 3:
- \( 9 \div 3 = 3 \)
- Start by dividing 225 by the smallest prime number, which is 5:
- Express as a Product of Prime Factors:
225 can be expressed as \( 5 \times 5 \times 3 \times 3 \), which simplifies to:
\( 225 = 5^2 \times 3^2 \)
- Group the Prime Factors into Pairs:
Pair the prime factors to simplify finding the square root:
\( 225 = (5 \times 3) \times (5 \times 3) = 15 \times 15 \)
- Take the Square Root of Each Pair:
Since \( 15 \times 15 = 225 \), the square root of 225 is:
\( \sqrt{225} = 15 \)
By following these steps, we see that the square root of 225 is 15. This method not only finds the square root but also illustrates the composition of the number in terms of its prime factors, providing a deeper understanding of its properties.
Exponent Method
The exponent method is a straightforward and efficient way to find the square root of a number by using the properties of exponents. Here’s a step-by-step guide to finding the square root of 225 using the exponent method:
- Understand the Relationship between Exponents and Roots:
The square root of a number can be expressed as an exponent. Specifically, the square root of a number \( n \) is the same as raising \( n \) to the power of \( \frac{1}{2} \).
In mathematical terms:
\( \sqrt{n} = n^{\frac{1}{2}} \)
- Express 225 as a Power:
Identify a base number that, when squared, equals 225. Here, we know that 15 squared equals 225:
\( 15^2 = 225 \)
- Apply the Square Root:
Using the exponent rule for square roots, rewrite 225 in exponential form and then apply the square root:
\( \sqrt{225} = (15^2)^{\frac{1}{2}} \)
- Simplify the Exponent:
Multiply the exponents to simplify the expression:
\( (15^2)^{\frac{1}{2}} = 15^{2 \times \frac{1}{2}} = 15^1 = 15 \)
Therefore, using the exponent method, we find that the square root of 225 is 15. This method leverages the power of exponents to simplify the process of finding square roots, making it both quick and easy to understand.

Long Division Method
The long division method is a manual technique to find the square root of a number. This method involves a step-by-step division process, similar to traditional long division. Here’s a detailed guide to finding the square root of 225 using the long division method:
- Setup:
Write 225 and group the digits in pairs from right to left. For 225, we get two groups: 2 and 25.
- Find the Largest Square:
Identify the largest number whose square is less than or equal to the first group (2). This number is 1 because \(1^2 = 1\) and \(2 - 1 = 1\).
- Write 1 as the first digit of the quotient.
- Bring Down the Next Pair:
Bring down the next group of digits (25) to the remainder to make 125.
- Double the Quotient:
Double the current quotient (1) to get 2, and write it as the beginning of the new divisor.
- Find the Next Digit:
Find a digit (x) such that \(2x \times x \leq 125\). The number 5 works because \(25 \times 5 = 125\).
- Add 5 to the quotient, making it 15.
- Subtract \(25 \times 5 = 125\) from 125, resulting in a remainder of 0.
- Result:
The quotient is 15, so the square root of 225 is:
\(\sqrt{225} = 15\)
Using the long division method, we systematically determine that the square root of 225 is 15. This method, though manual, provides a clear and thorough understanding of how square roots can be calculated step by step.
Using a Calculator
Finding the square root of 225 using a calculator is a straightforward process. Here’s a step-by-step guide:
- Turn on the Calculator: Ensure your calculator is on and functioning properly.
- Select the Square Root Function: Most calculators have a square root button (
√) or a function key (usually labeled2ndorShift) that allows access to the square root function. - Input the Number: Type in 225. You can either type the number first and then press the square root button, or press the square root button first and then input the number, depending on your calculator model.
- Execute the Calculation: Press the
=orEnterbutton to perform the calculation. - View the Result: The calculator will display the result, which is 15.
Here’s a visual representation of the process:
| Step | Action | Button | Display |
| 1 | Turn on the calculator | ON |
N/A |
| 2 | Select square root function | √ |
N/A |
| 3 | Input the number 225 | 2 2 5 |
225 |
| 4 | Execute the calculation | = |
15 |
If you’re using a scientific calculator, you might need to press the 2nd or Shift button before accessing the square root function. In some cases, you can directly enter √225 and press = to get the result.
Using a calculator simplifies the process of finding square roots and ensures accuracy. This method is particularly useful for large numbers or when performing quick calculations.
Understanding Perfect Squares
Perfect squares are numbers that can be expressed as the product of an integer with itself. In other words, if \( n \) is an integer, then \( n^2 \) is a perfect square. For example, \( 225 \) is a perfect square because it can be expressed as \( 15 \times 15 \) or \( 15^2 \).
Here are some key characteristics and methods to identify perfect squares:
Characteristics of Perfect Squares
- Perfect squares always end with 0, 1, 4, 5, 6, or 9 in the decimal system.
- If a number ends in an even number of zeros, it might be a perfect square. For example, 400 (20^2) is a perfect square.
- The square root of a perfect square is always an integer.
Methods to Identify Perfect Squares
- Digital Roots: The digital root of a perfect square is always 1, 4, 7, or 9. The digital root is found by repeatedly summing the digits of the number until a single digit is obtained. For example, the digital root of 225 is 9 (2+2+5=9).
- Modulo Operation: In modular arithmetic, perfect squares have specific remainders when divided by certain numbers. For example, a perfect square modulo 10 can only be 0, 1, 4, 5, 6, or 9.
- Prime Factorization: A number is a perfect square if all the prime factors appear an even number of times. For example, 225 can be factored into 3^2 \times 5^2, with each prime factor appearing twice.
- Square Root Test: The most definitive method is to take the square root of the number. If the result is an integer, the number is a perfect square. For instance, √225 = 15, which is an integer, thus confirming that 225 is a perfect square.
Examples of Perfect Squares
Here are some common perfect squares:
- 1 (1^2)
- 4 (2^2)
- 9 (3^2)
- 16 (4^2)
- 25 (5^2)
- 36 (6^2)
- 49 (7^2)
- 64 (8^2)
- 81 (9^2)
- 100 (10^2)
Understanding these patterns and methods can help you quickly identify perfect squares and utilize them effectively in various mathematical problems.
Visual Representation of Square Roots
Visualizing square roots can greatly enhance our understanding of the concept. Here, we explore different ways to represent square roots graphically, making it easier to grasp their meaning and significance.
Graphical Method
- Start by drawing a Cartesian coordinate system with an x-axis (horizontal) and a y-axis (vertical).
- Plot the function \( y = x^2 \) on the graph. This curve represents the square of \( x \).
- Identify the point where \( y \) equals 225. This is where the curve \( y = x^2 \) intersects the horizontal line \( y = 225 \).
- Draw a horizontal line from the y-axis at \( y = 225 \) until it meets the curve \( y = x^2 \).
- From the intersection point, draw a vertical line down to the x-axis. The x-coordinate of this intersection represents the square root of 225.
By observing the graph, you will see that the x-coordinate of the intersection point is 15, indicating that the square root of 225 is 15.
Square Root as Side Length of a Square
Another effective visual representation is to understand square roots as the side length of a square with a given area.
- Consider a square with an area of 225 square units.
- The side length of this square is the square root of 225.
- Since \( 15 \times 15 = 225 \), each side of the square measures 15 units.
This approach helps in visualizing how square roots relate to the geometry of squares.
Using Geometric Manipulatives
Manipulatives can also be used to approximate square roots. For example:
- Use paper squares to represent perfect squares and their approximations.
- For non-perfect squares, fill in the gaps with smaller pieces to approximate the square root.
These hands-on tools make abstract concepts more concrete and understandable.
Interactive Tools
Interactive graphing tools, such as Desmos, allow you to plot functions and visually explore the properties of square roots. These tools provide a dynamic way to learn and understand square roots through visual manipulation and observation.
By leveraging these various methods, you can gain a deeper and more intuitive understanding of square roots and their applications.

Historical Methods for Finding Square Roots
Finding the square root of a number has been a mathematical challenge tackled by various civilizations throughout history. Here are some historical methods used to determine square roots:
1. Babylonian Method (Heron's Method)
The Babylonian method, also known as Heron's method, dates back to ancient Babylon around 1800 BCE. It is an iterative method that uses the following steps:
- Start with an initial guess \( x_0 \).
- Improve the guess by averaging it with the quotient of the number and the guess: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \).
- Repeat the process until the desired accuracy is achieved.
For example, to find \( \sqrt{225} \) with an initial guess \( x_0 = 15 \):
- First iteration: \( x_1 = \frac{1}{2} \left( 15 + \frac{225}{15} \right) = 15 \).
- Since 15 is already the exact square root, no further iterations are needed.
2. Ancient Indian Method
The ancient Indian mathematicians used a method similar to the Babylonian method, which involved the use of successive approximations. They also documented algorithms for extracting square roots in their mathematical texts.
3. Chinese Method
The ancient Chinese had their own method for finding square roots, recorded in texts such as "The Nine Chapters on the Mathematical Art" (九章算术). Their approach was also iterative and closely related to the methods used by the Babylonians and Indians.
4. Greek Method
The Greek mathematicians, including Pythagoras and Euclid, made significant contributions to the understanding of square roots. Euclid's Elements contains geometric methods for finding square roots using the properties of similar triangles.
5. Medieval Islamic Method
During the Islamic Golden Age, mathematicians like Al-Khwarizmi and Al-Karaji further developed methods for extracting square roots. They used algebraic techniques and wrote extensively on the topic in their mathematical treatises.
6. European Renaissance Method
In Europe, methods for finding square roots continued to evolve during the Renaissance. Mathematicians like Fibonacci introduced the method of using prime factorization, and later, the development of logarithms provided a new tool for approximating square roots.
These historical methods laid the foundation for modern techniques used today, demonstrating the universal challenge and fascination with finding square roots across different cultures and eras.
Practical Applications of Square Roots
Square roots have numerous practical applications in various fields such as engineering, physics, architecture, and everyday problem-solving. Below are some examples of how square roots are used in different scenarios:
1. Calculating Areas
If you know the area of a square, you can find the length of its sides by taking the square root of the area. For example, if a square has an area of 225 square units, the length of each side is:
\(\sqrt{225} = 15\) units.
2. Physics - Gravity
In physics, the time it takes for an object to fall to the ground can be calculated using the formula:
\[ t = \frac{\sqrt{h}}{4} \]
where \( h \) is the height in feet. For instance, if an object is dropped from a height of 64 feet, the time to reach the ground is:
\[ t = \frac{\sqrt{64}}{4} = \frac{8}{4} = 2 \text{ seconds} \]
3. Accident Investigation
Police use square roots to determine the speed of a car before it started braking. If the length of the skid marks is \( d \) feet, the speed \( s \) can be estimated using the formula:
\[ s = \sqrt{24d} \]
For example, if the skid marks are 190 feet long, the speed of the car was approximately:
\[ s = \sqrt{24 \times 190} \approx 67.5 \text{ mph} \]
4. Construction and Design
Architects and engineers use square roots to determine dimensions and proportions. For example, to find the side length of a square room with an area of 256 square feet:
\(\sqrt{256} = 16\) feet.
5. Electrical Engineering
In electrical engineering, the root mean square (RMS) value of an alternating current (AC) is calculated using the square root of the average of the squares of the instantaneous values. This is important for designing and analyzing electrical circuits.
6. Standard Deviation in Statistics
The square root is used in statistics to calculate the standard deviation, which measures the amount of variation or dispersion in a set of values. The standard deviation is the square root of the variance.
These examples illustrate the importance and versatility of square roots in solving real-world problems efficiently and accurately.
Advanced Techniques for Finding Square Roots
Finding the square root of a number, especially large or non-perfect squares, can be challenging. Here, we explore some advanced techniques to simplify the process:
1. Approximation Method
The approximation method involves finding two perfect squares between which the given number lies. For instance, to find the square root of 225:
- Identify the nearest perfect squares: \(196\) (\(14^2\)) and \(256\) (\(16^2\)).
- Since \(225\) is closer to \(196\), start with \(14\) as an approximate square root.
- Refine the estimate using the formula: \[ \text{New Estimate} = \frac{\text{Old Estimate} + \frac{\text{Number}}{\text{Old Estimate}}}{2} \]
- For \(225\), starting with \(15\): \[ \text{New Estimate} = \frac{15 + \frac{225}{15}}{2} = \frac{15 + 15}{2} = 15 \]
2. Newton-Raphson Method
This iterative method provides a highly accurate estimate. For the square root of \(225\), follow these steps:
- Start with an initial guess, say \(x_0 = 15\).
- Use the formula: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{225}{x_n} \right) \]
- Iterate until convergence: \[ x_1 = \frac{1}{2} \left( 15 + \frac{225}{15} \right) = 15 \]
3. Continued Fractions
This technique uses continued fractions to express square roots. The continued fraction for \(\sqrt{225}\) is:
\[
\sqrt{225} = 15 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \cdots}}}
\]
4. Using Logarithms
Logarithms can transform multiplication and division into addition and subtraction, simplifying root calculations:
- Use the properties of logarithms: \[ \log_{10}(225) = \log_{10}(15^2) = 2 \log_{10}(15) \]
- Then, \[ \sqrt{225} = 10^{\frac{\log_{10}(225)}{2}} = 10^{\frac{2 \log_{10}(15)}{2}} = 10^{\log_{10}(15)} = 15 \]
5. Prime Factorization
Factor the number into prime factors and then simplify:
\[
225 = 3^2 \times 5^2
\]
\[
\sqrt{225} = \sqrt{3^2 \times 5^2} = 3 \times 5 = 15
Common Mistakes and How to Avoid Them
Finding the square root of a number can be straightforward, but there are common mistakes that people often make. Understanding these mistakes and how to avoid them will help ensure accuracy.
-
Confusing Positive and Negative Roots:
One common mistake is to write both the positive and negative roots for a square root function. Remember, the principal square root of a number is always non-negative. For example, the correct expression is:
\(\sqrt{225} = 15\), not \(\pm 15\).
-
Incorrect Simplification of Radical Expressions:
When simplifying square roots, ensure that you factor out perfect squares correctly. For example:
\(\sqrt{36} = 6\), not \(\sqrt{36} = 3\sqrt{4}\).
-
Assuming Square Root of a Sum Equals Sum of Square Roots:
It is incorrect to assume that \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\). This is a common algebraic mistake. For example:
\(\sqrt{4 + 9} = \sqrt{13}\), not \(\sqrt{4} + \sqrt{9} = 2 + 3 = 5\).
-
Misinterpreting the Square Root of a Squared Number:
When dealing with squared numbers under a square root, ensure to consider the absolute value. For example:
\(\sqrt{x^2} = |x|\), not simply \(x\). This is because \(x\) could be negative.
-
Ignoring Units and Context:
In practical applications, units matter. Ensure that the units are appropriately considered when dealing with square roots in measurements.
By recognizing and avoiding these common mistakes, you can improve your accuracy and understanding of square roots.
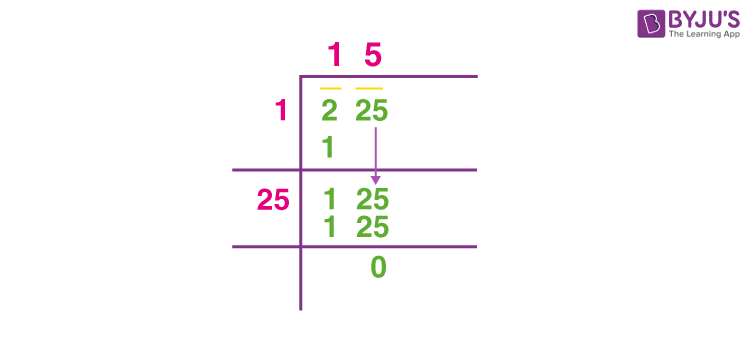
Frequently Asked Questions (FAQs)
-
What is the square root of 225?
The square root of 225 is 15 because \( 15 \times 15 = 225 \).
-
Why is the square root of 225 a rational number?
The square root of 225 is rational because 225 is a perfect square, which can be expressed as \( 15^2 \). Since 15 is a whole number, the square root is rational.
-
How do you calculate the square root of 225?
To calculate the square root of 225, find a number that, when multiplied by itself, equals 225. This number is 15.
-
What are the prime factors of 225?
The prime factors of 225 are \( 3^2 \times 5^2 \). This shows that 225 is composed of the prime numbers 3 and 5, each squared.
-
Is 225 a perfect square?
Yes, 225 is a perfect square because it can be expressed as \( 15^2 \).
-
How is the square root of 225 used in real life?
The square root of 225 is used in various real-life applications, such as finding the side length of a square with an area of 225 square units.
-
Can you find the square root of 225 using a calculator?
Yes, you can use a calculator to find the square root of 225. Simply enter 225 and use the square root function to get 15.
Conclusion
In conclusion, finding the square root of 225 can be approached through various methods, each with its unique advantages. Understanding these methods not only enhances mathematical skills but also provides a deeper appreciation of the underlying concepts. Here, we summarize the key techniques discussed:
- Prime Factorization Method: By expressing 225 as the product of its prime factors (3 × 3 × 5 × 5) and pairing them, we determine that √225 = 15.
- Exponent Method: Recognizing that 225 can be written as 152, we directly find that its square root is 15.
- Long Division Method: This method involves dividing the number 225 step-by-step, resulting in the quotient 15, which is the square root of 225.
- Using a Calculator: Simply inputting 225 into a calculator and using the square root function provides the answer 15 instantly.
These methods are not just theoretical exercises but have practical applications in various fields such as engineering, physics, and everyday problem-solving. Understanding perfect squares, like 225, and their properties can simplify complex calculations and enhance numerical literacy.
To summarize, the square root of 225 is 15, and mastering the different methods to find this value reinforces foundational mathematical skills that are essential in both academic and real-world contexts.
Cách Tìm Căn Bậc Hai của 225 bằng Phương Pháp Phân Tích Nhân Tử Nguyên Tố / Căn Bậc Hai của 225 / Căn Bậc Hai 225
READ MORE:
Tìm căn bậc hai của 225, 256, 20 và căn bậc hai của 40 mà không cần máy tính