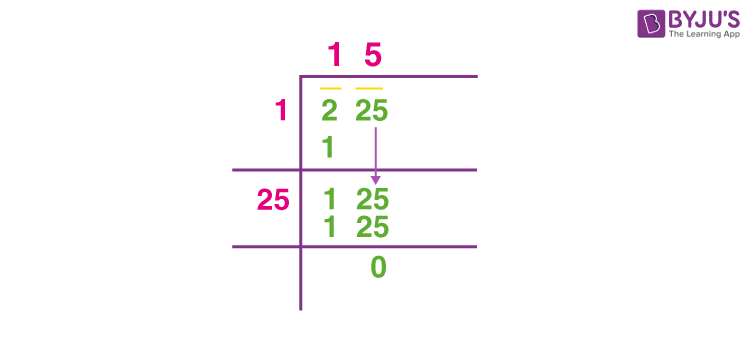Topic the square root of 256: The square root of 256 is a fundamental concept in mathematics, often encountered in various fields such as geometry, algebra, and physics. This article explores the calculation, properties, and real-world applications of the square root of 256, providing a comprehensive understanding of its significance and utility.
Table of Content
- Square Root Calculation
- Introduction
- What is a Square Root?
- Understanding Perfect Squares
- Calculation of the Square Root of 256
- Properties of the Square Root of 256
- Positive and Negative Square Roots
- Mathematical Representation
- Steps to Calculate Square Root Manually
- Using a Calculator for Square Root
- Real-World Applications of Square Roots
- Applications of the Square Root of 256 in Geometry
- Applications in Algebra
- Square Root in Physics
- Square Root in Computer Science
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Hướng dẫn cách tìm căn bậc hai của 256 bằng phương pháp phân tích nhân tử nguyên tố. Video chi tiết giúp bạn hiểu rõ về căn bậc hai của 256.
Square Root Calculation
The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 256, its square root can be determined as follows:
Definition
The square root of \(256\) is a number \(x\) such that:
\[ x^2 = 256 \]
Calculation
To find the square root of \(256\), we need to determine which number, when squared, equals \(256\). This can be represented as:
\[ \sqrt{256} = 16 \]
\[ 16 \times 16 = 256 \]
Properties
The square root of \(256\) has some interesting properties:
- It is a perfect square because \(256\) is the square of \(16\).
- It is an integer and specifically, a positive integer.
- Square roots can also be negative, so the negative square root of \(256\) is \(-16\).
Applications
Understanding the square root of \(256\) can be useful in various mathematical and real-world applications:
- Geometry: Calculating the side length of a square with an area of \(256\) square units.
- Algebra: Solving quadratic equations where \(256\) might be the constant term.
- Physics: Understanding formulas that involve squared quantities.
Table of Some Perfect Squares
Below is a table of some perfect squares to give a better understanding:
| Number | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 16 | 256 |
As demonstrated, the square root of \(256\) is an integral part of mathematics with diverse applications in different fields.

READ MORE:
Introduction
The square root of 256 is an essential mathematical concept that has numerous applications in various fields. The square root operation finds a number which, when multiplied by itself, gives the original number. For 256, this number is 16.
Mathematically, this is expressed as:
\[ \sqrt{256} = 16 \]
Let's explore the concept in detail:
- Understanding Square Roots: The square root is a value that produces the original number when squared.
- Perfect Squares: 256 is a perfect square, meaning it is the square of an integer.
- Calculation: The square root of 256 can be calculated manually or using a calculator.
- Applications: This concept is used in geometry, algebra, physics, and various real-world scenarios.
In this article, we will delve into the calculation, properties, and applications of the square root of 256, providing a comprehensive understanding of its significance and utility.
What is a Square Root?
A square root of a number is a value that, when multiplied by itself, yields the original number. It is a fundamental concept in mathematics, often used in various calculations and problem-solving scenarios.
Mathematically, the square root of a number \( x \) is denoted as \( \sqrt{x} \). This can be expressed as:
\[ \sqrt{x} = y \quad \text{if and only if} \quad y^2 = x \]
For example, the square root of 256 is 16 because:
\[ 16^2 = 256 \]
Key points to understand about square roots:
- Principal Square Root: The principal square root is the non-negative square root of a number. For any positive number \( x \), the principal square root is denoted by \( \sqrt{x} \).
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For 256, the square roots are \( 16 \) and \( -16 \).
- Perfect Squares: Numbers like 256 that have integer square roots are called perfect squares.
- Symbol: The square root symbol is √, which is called the radical sign.
The square root operation is widely used in geometry, algebra, and various fields of science and engineering. It helps in solving equations, understanding shapes and spaces, and analyzing physical phenomena.
By understanding square roots, one gains a deeper appreciation of the structure and properties of numbers, enhancing mathematical problem-solving skills and logical thinking.
Understanding Perfect Squares
A perfect square is a number that can be expressed as the product of an integer with itself. In other words, if \( n \) is an integer, then \( n^2 \) is a perfect square. Perfect squares are fundamental in various areas of mathematics and have several unique properties.
Here are some key points to understand perfect squares:
- A perfect square always has an integer square root.
- The square root of a perfect square is always an integer.
- Perfect squares are always non-negative, as squaring a number (whether positive or negative) results in a non-negative number.
- The number of positive divisors of a perfect square is always odd.
- Perfect squares can be visualized as squares of dots in a grid, making them useful in geometric interpretations.
Some common examples of perfect squares include:
| Integer | Perfect Square |
|---|---|
| 1 | \(1^2 = 1\) |
| 2 | \(2^2 = 4\) |
| 3 | \(3^2 = 9\) |
| 4 | \(4^2 = 16\) |
| 5 | \(5^2 = 25\) |
| 10 | \(10^2 = 100\) |
| 16 | \(16^2 = 256\) |
To determine if a number is a perfect square, you can use prime factorization. A number is a perfect square if all the exponents in its prime factorization are even. For example:
Consider the number 256:
- Prime factorize 256: \( 256 = 2^8 \).
- Since the exponent 8 is even, 256 is a perfect square.
- Thus, \( 256 = 16^2 \).
Perfect squares have various applications in real-world scenarios, including geometry, algebra, and computer science. Understanding perfect squares can enhance your comprehension of more complex mathematical concepts.
Calculation of the Square Root of 256
The square root of 256 can be calculated using several methods. Here, we will discuss two popular methods: the prime factorization method and the long division method.
Prime Factorization Method
This method involves breaking down the number into its prime factors and then grouping them to find the square root.
- Start by expressing 256 as a product of prime factors:
\[
256 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^8
\] - Next, pair the prime factors:
\[
2^8 = (2 \times 2) \times (2 \times 2) \times (2 \times 2) \times (2 \times 2) = (2^4)^2
\] - Take one number from each pair:
\[
\sqrt{256} = \sqrt{(2^4)^2} = 2^4 = 16
\]
Long Division Method
The long division method is a systematic way to find the square root of a number by dividing and finding the quotient step by step. Here’s how you can calculate the square root of 256 using this method:
- Write the number 256 and pair the digits from the right, giving us (02)(56).
- Find the largest number whose square is less than or equal to the first pair (02). In this case, it is 1:
\[
1 \times 1 = 1
\]Subtract and bring down the next pair:
\[
02 - 1 = 1, \text{ bring down 56 to make 156}
\] - Double the quotient (1) to get the new divisor (2). Find the largest digit (x) such that \(2x \times x \leq 156\). Here, \(x = 6\):
\[
26 \times 6 = 156
\] - Subtract and bring down the next pair if any. Since the remainder is now 0, we have found our quotient:
\[
\sqrt{256} = 16
\]
Conclusion
Using both the prime factorization and long division methods, we find that the square root of 256 is 16.

Properties of the Square Root of 256
The square root of 256 exhibits several interesting properties that are valuable in various mathematical contexts. Here, we outline some key properties of the square root of 256:
- Perfect Square: 256 is a perfect square because it can be expressed as \(16 \times 16\). Thus, the square root of 256 is 16.
- Principal and Negative Roots: The principal (positive) square root of 256 is 16. However, there is also a negative square root, -16, since \((-16) \times (-16) = 256\).
- Exponential Form: The square root of 256 can be expressed in exponential form as \(256^{1/2}\) or \(256^{0.5}\).
- Rational Number: The square root of 256 is rational because it can be expressed as the fraction \(16/1\).
- Even Integer: Since both 256 and its square root 16 are even numbers, the square root of an even number is always even.
- Multiplication Property: For any positive numbers \(a\) and \(b\), the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) holds true. For example, \(\sqrt{256} = \sqrt{16 \times 16} = \sqrt{16} \times \sqrt{16} = 16\).
- Sum of Odd Numbers: The square of a number \(n\) is equal to the sum of the first \(n\) odd numbers. For 16, \(16^2 = 1 + 3 + 5 + ... + 31 = 256\).
- Digit Properties: If a number ends with the digit 6, its square root will also end with either 4 or 6. In the case of 256, the last digit 6 leads to the square root ending in 6 (as 16).
- Positive and Negative Values: Both \( \sqrt{256} \) and \(-\sqrt{256}\) are valid square roots, representing 16 and -16 respectively.
These properties not only enhance our understanding of the number 256 but also illustrate broader principles applicable to other perfect squares and their roots.
Positive and Negative Square Roots
The concept of square roots includes both positive and negative values. When we refer to the square root of a number, we are often talking about the principal (positive) square root, but it's important to remember that every positive number actually has two square roots: one positive and one negative.
For instance, the square root of 256 can be both +16 and -16 because:
This can be expressed as:
When considering the principal square root, we use the positive value. Thus, the principal square root of 256 is 16. However, in contexts where both roots are relevant, it is important to acknowledge both +16 and -16.
Mathematically, this can be represented as:
- The principal square root:
- The negative square root:
Understanding that every positive number has both a positive and negative square root is crucial for solving various mathematical problems, especially in algebra and calculus.
Mathematical Representation
The mathematical representation of the square root of 256 can be expressed in various forms. Here are the key representations:
- Radical Form: The most straightforward representation of the square root of 256 is using the radical sign, which is written as \( \sqrt{256} \).
- Exponential Form: The square root of 256 can also be represented using exponents. This is written as \( 256^{\frac{1}{2}} \) or \( 256^{0.5} \).
Radical Form
In radical form, the square root of 256 is written as:
\[ \sqrt{256} = 16 \]
This is because 16 multiplied by itself equals 256:
\[ 16 \times 16 = 256 \]
Exponential Form
In exponential form, the square root of 256 is expressed as:
\[ 256^{\frac{1}{2}} = 16 \]
Here, raising 256 to the power of 1/2 gives the same result as taking the square root.
Properties
The square root of 256 has several important properties:
- Perfect Square: 256 is a perfect square because its square root is an integer. In this case, 256 is the square of 16.
- Rational Number: The square root of 256 is a rational number since it can be expressed as the fraction \(\frac{16}{1}\).
- Positive and Negative Roots: Mathematically, both 16 and -16 are square roots of 256 because both satisfy the equation \( x^2 = 256 \). However, by convention, the principal square root is the positive value.
Equations and Notations
The square root function can be applied in various mathematical contexts, such as solving equations and simplifying expressions:
- In solving the quadratic equation \( x^2 = 256 \), we find:
- In algebraic notation, the square root is often used to simplify expressions and solve for variables.
\[ x = \pm \sqrt{256} \]
\[ x = \pm 16 \]
Overall, the square root of 256 is a fundamental mathematical concept with various representations and properties that are useful in different branches of mathematics, including algebra and geometry.
Steps to Calculate Square Root Manually
Calculating the square root manually involves a few different methods. Below, we describe the prime factorization method and the long division method in detail.
Prime Factorization Method
In the prime factorization method, you break down the number into its prime factors and then pair them. Here are the steps to calculate the square root of 256:
- First, divide 256 by the smallest prime number, which is 2:
- 256 ÷ 2 = 128
- 128 ÷ 2 = 64
- 64 ÷ 2 = 32
- 32 ÷ 2 = 16
- 16 ÷ 2 = 8
- 8 ÷ 2 = 4
- 4 ÷ 2 = 2
- 2 ÷ 2 = 1
- Express 256 as the product of its prime factors:
- Group the prime factors into pairs:
- Take one number from each pair:
- So, the square root of 256 is:
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
(2 × 2) × (2 × 2) × (2 × 2) × (2 × 2)
2 × 2 × 2 × 2 = 16
√256 = 16
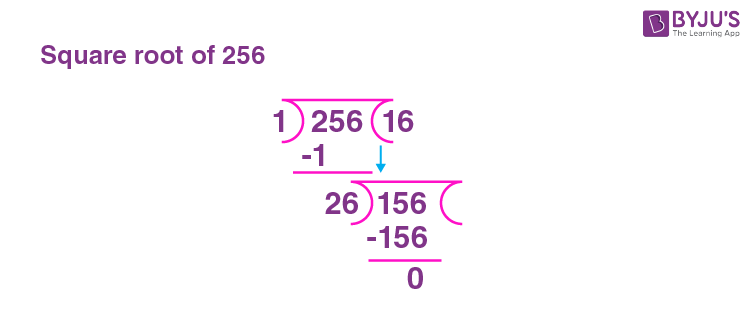
Long Division Method
The long division method is another way to find the square root of a number, especially when it’s not a perfect square. Here are the steps to calculate the square root of 256:
- Group the digits of the number in pairs starting from the decimal point. For 256, it is already a whole number, so pair it as 2 and 56.
- Find the largest number whose square is less than or equal to the first pair (2). The largest such number is 1 (since 1×1=1).
- Subtract the square of this number from the first pair and bring down the next pair to the right of the remainder. This gives us 156.
- Double the divisor and write it down (2×1=2), then find a digit to add to the divisor (2X) such that when the new number is multiplied by this digit, it is less than or equal to 156. This digit is 6 (since 26×6=156).
- Subtract and continue the process until no remainder is left. Here, 156 - 156 = 0, and we stop.
- The quotient at this stage is the square root of 256.
The detailed steps for the long division method are as follows:
- 256 is grouped into (2)(56).
- The largest number whose square is ≤ 2 is 1.
- Subtract 1² from 2 to get 1 and bring down the 56 to get 156.
- Double the divisor (1×2=2). Find X such that 2X×X ≤ 156. Here, X=6 (since 26×6=156).
- Subtract 156 from 156 to get 0. The quotient is 16.
Therefore, the square root of 256 is 16.
By following these steps, you can manually calculate the square root of any perfect square.
Using a Calculator for Square Root
Calculating the square root of a number using a calculator is a straightforward process. Here are the detailed steps to find the square root of 256:
-
Turn on the Calculator: Ensure that your calculator is powered on and functioning properly.
-
Select the Square Root Function: Most calculators have a dedicated square root button (√). On scientific calculators, this button is usually located on the left side. On some basic calculators, you might need to press the 'Shift' or '2nd' key to access the square root function.
-
Enter the Number: Input the number for which you want to find the square root. In this case, type 256.
-
Calculate the Square Root: Press the square root button (√). The calculator will display the square root of 256.
-
Result: The calculator should display the result, which is 16.
Below is an example of using a calculator to find the square root:
| Input | Operation | Result |
| 256 | Press √ | 16 |
Using an online square root calculator can also be very convenient. You simply enter the number, and the calculator will provide the square root. Here is how you can use an online calculator:
- Visit a reliable square root calculator website.
- Enter 256 into the input box.
- Click the 'Calculate' or 'Find Square Root' button.
- The result will be displayed as 16.
Using a calculator ensures accuracy and saves time, especially when dealing with large numbers or decimal values.
Real-World Applications of Square Roots
Square roots have a variety of real-world applications in different fields such as geometry, physics, and engineering. Here are some detailed examples:
-
Geometry:
Square roots are used to determine the side length of a square when the area is known. For example, if a square has an area of 256 square units, the side length is the square root of 256, which is 16 units.
-
Physics:
Square roots are used in physics to calculate the time it takes for an object to fall to the ground. The formula is \( t = \sqrt{\frac{2h}{g}} \), where \( t \) is the time, \( h \) is the height, and \( g \) is the acceleration due to gravity. For instance, an object dropped from a height of 64 feet takes \( \sqrt{\frac{2 \times 64}{32}} = \sqrt{4} = 2 \) seconds to reach the ground.
-
Engineering:
Engineers use square roots to calculate stress and strain in materials. The square root function helps in determining the load that different structures can withstand.
-
Accident Investigation:
In accident investigations, police use the length of skid marks to determine the speed of a vehicle before braking. The formula \( v = \sqrt{24d} \) is used, where \( v \) is the speed and \( d \) is the length of the skid marks. For example, if the skid marks are 190 feet long, the speed is \( \sqrt{24 \times 190} \approx 67.5 \) miles per hour.
These examples illustrate the importance and practical applications of square roots in everyday life, making them a fundamental concept in mathematics and science.
Applications of the Square Root of 256 in Geometry
The square root of 256, which is 16, has various applications in geometry. Here are some key applications:
1. Calculating Side Lengths of Squares
If the area of a square is 256 square units, then each side length of the square is the square root of 256. Therefore, the side length is 16 units.
For example:
- Area of the square: 256 square units
- Side length = √256 = 16 units
2. Determining Dimensions of Right Triangles
In a right triangle, the square root of 256 can be used to find the length of the hypotenuse or the legs, depending on the given dimensions. For instance, if one leg of a right triangle is 16 units, and the hypotenuse is found using the Pythagorean theorem (a² + b² = c²), we can calculate other dimensions.
For example:
- One leg (a): 16 units
- Hypotenuse (c): 16√2 units
3. Area of an Equilateral Triangle
The square root of 256 is used in finding the side length of an equilateral triangle when its area is given. If the area of an equilateral triangle is 256√3 square units, the length of each side can be calculated as follows:
Given the formula for the area of an equilateral triangle:
Setting this equal to 256√3 and solving for 'a' (the side length), we get:
4. Volume of a Cube
The square root of 256 can also apply in three-dimensional geometry, such as finding the volume of a cube where the length of an edge is 16 units (since √256 = 16). The volume of the cube is:
- Volume = side length³ = 16³ = 4096 cubic units
5. Perimeter of Geometric Shapes
In polygons and other geometric shapes, the square root of 256 can determine the perimeter when the side lengths involve this value. For example, the perimeter of a square with each side of 16 units is:
- Perimeter = 4 × side length = 4 × 16 = 64 units
These applications highlight the importance and practicality of understanding the square root of 256 in various geometric contexts.
Applications in Algebra
The square root of 256, which is 16, plays a significant role in various algebraic contexts. Here are some detailed applications:
-
Solving Quadratic Equations:
Quadratic equations often involve square roots in their solutions. For instance, the equation \( x^2 = 256 \) can be solved by taking the square root of both sides, resulting in \( x = \pm 16 \).
Example:
\[
x^2 = 256 \\
x = \pm \sqrt{256} \\
x = \pm 16
\] -
Exponential Functions:
The square root function is an inverse of squaring and is essential in simplifying expressions involving exponents. For example, the expression \( 256^{1/2} \) simplifies to 16.
Example:
\[
256^{1/2} = \sqrt{256} = 16
\] -
Distance Formula:
In coordinate geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
If the squared distance is 256, then \( d = \sqrt{256} = 16 \). -
Pythagorean Theorem:
In right-angled triangles, the relationship between the sides can be expressed using the Pythagorean theorem:
\[
a^2 + b^2 = c^2
\]
If one of the sides is the square root of 256, then the length of that side is 16. -
Area and Volume Calculations:
Square roots are used to determine dimensions from area or volume. For a square with an area of 256 square units, the side length is:
\[
s = \sqrt{256} = 16
\]
Similarly, for a cube with a volume of 256 cubic units, the side length is also:
\[
s = \sqrt[3]{256} = 2 \sqrt{64} = 2 \times 8 = 16
\]
These examples illustrate the importance of square roots, particularly the square root of 256, in algebraic operations and problem-solving.
Square Root in Physics
The concept of square roots plays a crucial role in various areas of physics. One of the fundamental applications of the square root of 256, which is 16, is in understanding and solving physical equations and phenomena. Here are some detailed applications:
1. Wave Mechanics
In wave mechanics, the wavelength (\(\lambda\)) of a wave is related to the wave speed (v) and frequency (f) by the equation:
\[
\lambda = \frac{v}{f}
\]
If the speed of a wave is given as 256 meters per second and the frequency is 16 Hz, then the wavelength can be calculated using the square root:
\[
\lambda = \frac{256 \, \text{m/s}}{16 \, \text{Hz}} = 16 \, \text{meters}
\]
2. Kinetic Energy
The kinetic energy (K.E.) of an object is given by the formula:
\[
K.E. = \frac{1}{2}mv^2
\]
where m is the mass and v is the velocity. If an object has a kinetic energy of 2048 Joules and a mass of 16 kg, the velocity can be found as follows:
\[
2048 = \frac{1}{2} \times 16 \times v^2
\]
\[
2048 = 8v^2
\]
\[
v^2 = \frac{2048}{8} = 256
\]
\[
v = \sqrt{256} = 16 \, \text{m/s}
\]
3. Gravitational Potential Energy
Gravitational potential energy (G.P.E.) near the Earth's surface is given by:
\[
G.P.E. = mgh
\]
where m is the mass, g is the acceleration due to gravity (approximately \(9.8 \, \text{m/s}^2\)), and h is the height. For an object of mass 16 kg raised to a height such that its potential energy is 1568 Joules, the height can be calculated as:
\[
1568 = 16 \times 9.8 \times h
\]
\[
h = \frac{1568}{16 \times 9.8} = \frac{1568}{156.8} = 10 \, \text{meters}
\]
Using the square root, if instead, we consider the object to be raised to a height calculated by the square root of 256:
\[
h = \sqrt{256} = 16 \, \text{meters}
\]
4. Acoustic Physics
In acoustic physics, the intensity level of sound (measured in decibels) often uses the logarithmic scale where square roots are applied. The root mean square (RMS) value of sound pressure is a measure used in these calculations.
These examples illustrate how the square root of 256, which simplifies to 16, is frequently used in physics to solve for various physical quantities, demonstrating the pervasive nature of square roots in the field.
Square Root in Computer Science
The square root of 256 finds significant applications in various fields of computer science. Some of the key areas where it is utilized include algorithm optimization, computer graphics, cryptography, and computational efficiency.
Algorithm Optimization
Algorithms often use square roots for optimization purposes. For instance, in search algorithms like Grover's algorithm in quantum computing, the number of operations required to find an item in an unsorted database is proportional to the square root of the number of items, providing a quadratic speedup compared to classical algorithms.
Grover's algorithm performs in
Computer Graphics
In computer graphics, calculating distances between points, lengths of vectors, and other geometric transformations often require square root operations. For example, the Euclidean distance formula between two points
This formula is fundamental in rendering scenes and processing images.
Cryptography
Square roots play a crucial role in cryptographic algorithms. For example, in certain public-key cryptographic systems, the security relies on the difficulty of computing discrete square roots modulo a large prime number. Additionally, the RSA encryption algorithm involves operations with large prime numbers, where square roots are part of the underlying mathematical concepts.
Computational Efficiency
Square root calculations are integral to numerous computational problems and optimization techniques. One famous example is the "fast inverse square root" algorithm used in computer graphics, particularly in the development of the Quake III Arena game. This algorithm allows for rapid calculation of normalized vectors, essential for efficient rendering and physics calculations.
The algorithm approximates the inverse square root with a clever use of bit manipulation and Newton's method for refinement, dramatically speeding up the computations compared to traditional methods:
float Q_rsqrt(float number) {
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y;
i = 0x5f3759df - ( i >> 1 );
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) );
return y;
}
This method significantly boosts performance in real-time applications where computational efficiency is paramount.
Conclusion
Overall, the square root of 256, like other square root values, is deeply embedded in various aspects of computer science, from theoretical algorithms to practical applications in graphics and cryptography. Its computational properties enable efficient and effective solutions to complex problems.
Frequently Asked Questions
-
What is the square root of 256?
The square root of 256 is 16. This is because 16 multiplied by itself (16 × 16) equals 256.
-
Why is the square root of 256 a rational number?
The square root of 256 is rational because 256 is a perfect square. Its prime factorization is \(2^8\), and the square root is \(2^4 = 16\), which is an integer.
-
Is 256 a perfect square?
Yes, 256 is a perfect square. This means its square root is a whole number. In this case, \(16\).
-
What is the square root of -256?
The square root of -256 is an imaginary number. It can be written as \(\sqrt{-256} = \sqrt{-1} \times \sqrt{256} = 16i\), where \(i\) is the imaginary unit representing \(\sqrt{-1}\).
-
How do you represent the square root of 256 using exponents?
The square root of 256 can be expressed using exponents as \(256^{1/2}\). This is another way to denote \(\sqrt{256}\).
-
Can the square root of 256 be simplified?
Since 256 is already a perfect square, its square root is already in its simplest form, which is 16.
-
How can you calculate the square root of 256 manually?
To calculate the square root of 256 manually, you can use the long division method:
- Pair the digits of 256 from right to left: (2)(56).
- Find the largest number whose square is less than or equal to the first pair (2). This is 1, since \(1^2 = 1\).
- Subtract 1 from 2, getting 1, and bring down the next pair of digits (56), making 156.
- Double the quotient obtained so far (1) to get 2, and find a digit x such that 2x multiplied by x is less than or equal to 156. The correct digit is 6 (since \(26 \times 6 = 156\)).
- Since there is no remainder, the square root of 256 is 16.
-
What are some real-world applications of the square root of 256?The square root of 256 can be used in various fields such as geometry, algebra, physics, and computer science. For example, in geometry, it can be used to find the side length of a square with an area of 256 square units.
Conclusion
The square root of 256 is a significant mathematical concept with various applications in different fields such as geometry, algebra, physics, and computer science. Its exact value is 16, and it is obtained through methods like prime factorization, long division, and approximation.
Understanding the properties of the square root of 256 helps in grasping broader mathematical principles. For instance, it demonstrates that 256 is a perfect square, which simplifies calculations in both theoretical and practical scenarios. The number 256 can be factored into \(2^8\), which underlines its structure and ease of computation.
Moreover, recognizing that 256 has both positive and negative square roots (±16) extends its relevance in solving equations and in complex number calculations where imaginary numbers are involved. This duality also highlights the importance of considering all potential solutions in mathematical problems.
In real-world applications, the square root of 256 is utilized in diverse areas including construction, where it might be used to determine dimensions of square areas, in technology for data representation, and in sciences for solving physical equations.
Ultimately, mastering the calculation and implications of the square root of 256 not only enhances mathematical literacy but also equips individuals with the skills to apply this knowledge practically and accurately in various domains.

Hướng dẫn cách tìm căn bậc hai của 256 bằng phương pháp phân tích nhân tử nguyên tố. Video chi tiết giúp bạn hiểu rõ về căn bậc hai của 256.
Cách Tìm Căn Bậc Hai Của 256 Bằng Phương Pháp Phân Tích Nhân Tử Nguyên Tố / Căn Bậc Hai Của 256 / 256 Căn Bậc Hai
READ MORE:
Khám phá cách tìm căn bậc hai của 256 trong video này. Hướng dẫn chi tiết và dễ hiểu giúp bạn nắm vững kiến thức về căn bậc hai của 256.
Căn Bậc Hai Của 256